考虑相关因素统一修正的节假日负荷预测模型

苗键强，童星，康重庆

(电力系统及发电设备控制和仿真国家重点实验室(清华大学电机系)，北京市 100084)



考虑相关因素统一修正的节假日负荷预测模型

苗键强，童星，康重庆

(电力系统及发电设备控制和仿真国家重点实验室(清华大学电机系)，北京市 100084)

能源互联网正在逐步影响电网的规划建设方式，其对于相关的负荷预测技术也提出了更高的要求。节假日负荷预测由于存在与正常工作日差异较大且历史数据较少的原因，其负荷预测的效果往往不理想。通过相关因素统一修正模型对气象、时间等相关因素进行修正处理之后，得到统一相关因素影响下的正常工作日数据。考虑“近大远小”的原则，对于正常工作日和节假日负荷曲线之间的相关性进行分析，并基于点对点倍比预测模型提出节假日负荷预测模型，该模型能够自动削弱历史中不正常数据对于预测精度的影响。将提出的预测方法应用于我国北方某城市和某地区的节假日负荷预测，算例分析结果显示预测精度能够满足实际需要，可以为相关电力部门节假日负荷预测提供一定的参考价值。

负荷预测；节假日；相关因素；点对点倍比

0 引言

以新能源技术和互联网技术为代表的能源互联网建设对于传统的电力系统建设规划产生了巨大的影响。新的经济和社会发展模式需要更加精确的负荷预测技术为支撑，这对于其中相对历史数据和经验较少的节假日负荷预测也提出了更高的要求。

对于短期负荷预测，常用的预测方法包括时间序列法[1-2]、频域分量法[3-4]、小波分析法[5-6]、混沌理论预测[7-8]、人工神经网络[9-10]、支持向量机[11-12]等等，这些方法往往是基于大量已有的同类型历史数据。然而，节假日负荷预测由于其变化规律与正常工作日存在明显差异，且历史相关数据量较少等原因[13]，采用这些方法预测的精度也难以满足实际要求。

前人对于节假日的负荷预测进行了比较详细的研究。相关的研究工作如下：(1)通过选取气象等外部条件相似的双休日为基准，用历年春节负荷与双休日负荷的比例来修正、预测节假日最大负荷[14]；(2)通过采用相似日法获得节假日负荷曲线的变化情况，并基于之前的节假日负荷水平，用负荷水平的年增长率进行修正从而得到节假日负荷曲线和最大负荷的预测结果[15]；(3)基于统计规律预测节假日负荷，再根据“近大远小”的原则得到理念节假日负荷和节前正常工作日的负荷的平均值，通过比较各年节假日负荷和正常负荷，得到负荷增长率，进而求得待预测节假日负荷[16]；(4)采用模糊逻辑，以节假日、日期、最高气温和最低气温为模糊输入变量，将最高负荷和最低负荷作为输出变量，依据历史经验建立模糊规则，最终得到节假日的预测负荷水平[17]。在这些预测方法中，对于气象等相关因素影响的修正是一个重要环节。然而，文献[18]指出，以往分析模型中的气象因素修正模型还有待完善，需要更加合理地考虑气象因素对负荷的影响。

在以往的预测方法中，为消除部分异常数据对于预测结果的影响，在进行数据相关性分析时往往首先识别并剔除异常数据，该方法可以有效提升预测精度[19]。而在本文工作中，考虑通过模型自适应方式自动削弱历史数据中的异常数据，进而不再需要异常数据剔除模块。算例结果显示该方法预测的精度仍然能够满足实际需求。

在对于节假日负荷预测的实现过程中，本文首先建立模型以消除气象、时间等主要相关因素对于电力负荷的影响，模型中的负荷均为标准相关因素，从而使得节假日因素成为影响负荷情况的最主要因素。在此基础上，基于节假日负荷预测中的负荷点对点倍比原理进行预测[20]。在预测模型的设计中，对于选取的历史数据进行了加权处理，使得对于节假日负荷更具有参考价值的数据在预测系统中占的权重越高，而由于数据异常导致参考价值不足的历史数据在预测系统中所占权重自动降低。将本文提出的方法应用于我国北方某地区2015年的节假日负荷预测，分析结果显示该模型具有良好的预测精度。

文章结构主要包括如下若干部分：第1节给出了预测模型的总体计算步骤；第2节给出了相关因素基础修正模型；基于相关因素统一修正的点对点倍比预测模型在第3节中描述；第4节基于某地近几年的实际数据对于预测模型的可行性和可靠性进行了验证；第5节总结了全文工作。

1 预测模型计算步骤

(1)初始化参数，包括选取逐点负荷平滑系数α，负荷修正强度k；

(2)选取历史参考日，记录本年度和上年度的相关历史参考日的负荷、气温、时间和日期类型，以及本年度待预测节假日当天的时间、日期类型以及气象预测数据；

(3)对数据进行相关因素修正，选取上年度和本年度的节假日当天的相关因素为基准，通过第2部分中的修正模型对工作日负荷进行修正；

(4)将处理之后的负荷数据代入第3部分中提出的点对点倍比预测模型，分别计算本年度和上年度节前相关日t时刻的平滑度，在此基础上计算待预测节假日t时刻的负荷预测值；

(5)依次对节假日当天的每个时刻的负荷值进行估算，得到待预测日的负荷曲线；

(6)对于预测结果进行分析评估。

2 相关因素修正模型

在负荷预测的研究中，气象、时间、日期类型是影响负荷变化规律的主要原因。相同的日期类型和相似的气象条件下的负荷情况往往较为相似。同时，在中长期时间尺度中，负荷随时间还会表现出长期的周期上升的变化规律。节假日负荷预测的结果也会受到这些因素的影响，因此，在分析节假日负荷变化规律之前先通过模型对这些因素进行统一修正得到的结果将较为合理地反应负荷与节假日之间的变化规律。

2.1 气象因素对负荷的影响修正

图1给出了某地区某年日用电量和平均气温之间的关系，通过分析二者的相互关系可以发现：电量和平均气温大致呈现二次函数关系。

图1 某地区电网日电量和平均温度关系Fig. 1 Relationship between daily energy consumption and average temperature in certain region

因此，为修正气温对于日电量的影响，采用如下模型进行回归分析：

y1t=aTavg2+bTavg+c

(1)

式中：t为日期；y为日电量；Tavg表示平均温度，a、b、c分别表示二次项、一次项之前的回归系数以及相应的常数项。

2.2 时间和日期类型因素对负荷影响的修正方法

日用电量不仅仅与星期、月份呈现一定的周期变化规律，同时随着时间呈现逐步递增的规律。对于用电量随时间呈现长期平稳发展的趋势，一般可以采用直线、二次曲线、指数曲线等模型进行拟合，文献[20]采用线性关系近似拟合负荷随时间长期变化的趋势。基于此的时间和日期类型修正模型可以表示为

(2)式中：dt反映的是电量随时间的线性增长趋势；符号函数s(i,j,t)来表征不同星期类型、不同月份的影响，当且仅当第t日的星期类型恰好等于i、月份恰好等于j时，s(i,j,t)的函数值才取1，否则，函数值一律为0；cij表示星期类型为i、月份为j时的回归常数项。

2.3 相关因素统一修正模型

在模型中统一修正气温、时间和日期类型对于负荷的影响，可以提出如下相关因素统一修正模型：

y3t=aTavg2+bTavg+

(3)

基于历史正常工作日的数据对于上述修正模型进行回归可以得出a,b,c,d的具体数值。进一步确定相关因素的标准参考条件为待测节假日当天的平均气温、日期类型，并根据参考日和节假日之间的时间间隔修正相关因素，可以得到历史正常工作日映射到节假日的负荷为

yH=aTavg,H2+bTavg,H+

(4)

其中下标H表示节假日当天的相关因素的具体数值。考虑历史实际节假日负荷为yh，则基于历史数据中的yh，yH以及待预测节假日之前的正常工作日对于待预测节假日负荷进行预测的点对点倍比预测模型将在第3节提出。

3 改进点对点倍比预测模型

对于节假日点对点倍比法，首先对于节前所选取的n个相关日进行由近到远的排序，距离待预测日最近的日期排序为第1天，距离最远的日期排序为第n天。

3.1 异常数据误差处理模型

3.1.1 高阶调和平均影响修正因子

通过对节前的相关日进行排序，得到参考负荷序列，通过第2节的相关因素统一修正模型可以得到相关因素均处于标准状态下的负荷序列。对于该负荷序列，其中的大多数负荷数据彼此都比较接近，对于其中的少数异常数据，其与周围的负荷数据的差异较大，因此，可以设计一定的修正方法降低异常数据在整个时间序列中的权重。总体设计需要考虑以下3点要求：

(1)对于两侧数据均为正常数据的情况，尽可能保留其在后续处理模型中的权重；

(2)对于异常数据，尽可能降低其在后续处理模型中的权重；

(3)对于一侧是异常数据一侧是正常数据的边缘数据，考虑到其数据本身的合理性，应当保留其在模型中的权重。

考虑上述3点要求，设计如下高阶调和平均影响修正因子：

(5)

式中：k和β为事先选取的常数，k表示高阶调和平均数的阶数，β为权重系数。

该修正因子的设计采用了调和平均数的特性，根据xi-1和xi+1的定义可知，如果时间序列中的第i个值为异常数据，则得到的xi-1和xi+1均显著大于0，则对应的高阶调和平均数ρi也显著大于0，进而求得的影响因子κi则显著小于1；如果序列中的第i个值为正常数据，且相邻数据均为正常数据，那么得到的xi-1和xi+1均接近于0，从而求得的影响因子κi接近于1；如果序列中的第i个值为边缘数据，则得到的xi-1和xi+1其中之一接近于0，另外一个显著大于0，进一步求得的高阶调和平均数ρi将更接近于数值小的x，进而一定程度上保留了边缘数据的影响权重。在实际修正过程中，k和β的数值越大，该修正模型对于正常数据和异常数据计算得到的影响因子的区分越明显，从而正常数据和异常数据在后续模型中占的权重的区别也更显著。

3.1.2 异常数据误差处理模型

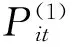
(6)

3.2 平滑值计算模型

假定计算t时刻，分别计算本年度和上年度节前相关日t时刻的平滑值A1t,A2t：

(7)

(8)

式中：α为逐点负荷的平滑系数，一般可取α∈[0.1，0.9]。

3.3 节假日负荷曲线预测模型

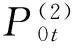
(9)

于是，待预测劳t时刻的负荷值为

(10)

按照该预测方法对于节假日当天的每个时刻的负荷值依次进行估算，可得该日的预测曲线。

4 算例分析

根据我国北方某城市和地区的真实数据来检验模型，在预测模型中以基准年前一年的相关节假日负荷数据为依准，对于基准年的元旦、春节、清明、五一以及端午节的负荷进行预测。

4.1 中国北方某城市劳动节负荷预测结果分析

我国北方某城市某年的劳动节负荷曲线预测结果和真实数据对比如图2所示。

相关结果表明预测结果在用电高峰区的预测精度较高，在用电低谷的预测精度相对较低，但总体预测精度在可以接受的范围内。

通过对各时段的负荷进行累加，可以得到日电量的预测值，表1给出了该市当年部分节假日的日电量的预测结果和真实结果的对比。

表1 部分节假日日电量预测结果和真实值对比

Table 1 Comparison between forecasting results and real facts of daily power consumption on some holidays

通过分析表1数据可以得出：不同节假日的相对误差基本上在可以接受的范围内。

4.2 中国北方某地区端午节负荷预测结果分析

该地区当年端午节的负荷曲线预测结果和实际结果对比如图3所示。

图3 端午节负荷预测结果和实际数据Fig. 3 Load forecasting results and real data on Dragon Boat Day

图3反映的预测结果与真实结果之间的关系和前一节中城市负荷预测结果反映的规律基本一致。表2给出了当天96个时刻预测结果的误差分布情况。

表2 各时刻负荷预测误差

Table 2 Timely load forecasting error

经过计算得到拟合的平均误差为0.77%，在可以接受的范围内。通过对各时段的负荷进行累加得到日电量的预测值，图4给出了当年部分法定节假日的日电量的预测结果和真实值的对比。

图4 该地区部分节假日日电量预测结果和真实值对比Fig. 4 Comparison between forecasting results and real facts of daily power consumption of some holidays

图4中的柱状部分分别表示该地区当年部分节假日的日电量预测值与真实值，折线部分表示预测值与真实值的相对差异。通过分析图4数据可以发现，该地区的预测结果和城市日电量的预测精度相似，不同节假日的相对误差基本上在可以接受的范围内，说明该模型具有一定的应用价值。

5 结 论

本文基于点对点倍比预测模型提出了一种将相关因素统一修正的节假日负荷预测方法。该方法首先通过气象、时间修正模型将相关因素进行统一修正，在此基础上基于以往历年节假日和节前正常工作日的负荷点对点倍比情况预测节假日负荷情况。该方法的各个分析模块相互独立，算法移植性较好，预测方案也相对简单实用。算例分析结果表明，该方法的预测精度可以满足实际的要求，从而能够为能源互联网新形势下电力系统的相关电力规划问题的解决提供一定的参考价值。

[1]雷绍兰．基于电力负荷时间序列混沌特性的短期负荷预测方法研究[D]．重庆：重庆大学，2005． Lei Shaolan．Research on short-term load forecasting model and method based on chaotic characteristic of electric load time series[D]．Chongqing：Chongqing University，2005．[2]Paparoditis E, Sapatinas T. Short-term load forecasting: the similar shape functional time-series predictor[J]. IEEE Transactions on Power Systems, 2013, 28(4): 3818-3825.

[3]任明明．基于频域分解的短期负荷预测研究[D]．乌鲁木齐：新疆大学，2013． Ren Mingming．The short-term load forecasting research based on frequency domain decomposition[D] Urumqi：Xinjiang University，2013．[4]Ghelardoni L, Ghio A, Anguita D. Energy load forecasting using empirical mode decomposition and support vector regression[J]. IEEE Transactions on Smart Grid, 2013, 4(1): 549-556.

[5]邰能灵，侯志俭，李涛，等．基于小波分析的电力系统短期负荷预测方法[J]．中国电机工程学报,2003,23(1):45-50. Tai Nengling, Hou Zhijian, Li Tao, et al. New principle based on wavelet transform for power system short-term load forecasting[J].Proceedings of the CSEE,2003,23(1):45-50.

[16]Pandey A S, Singh D, Sinha S K. Intelligent hybrid wavelet models for short-term load forecasting[J]. IEEE Transactions on Power Systems, 2010, 25(3): 1266-1273.

[7]杨正瓴，王渭巍，曹东波，等．短期负荷预测的Ensemble混沌预测方法[J]．电力系统自动化,2007,31(23):34-37. Yang Zhengling, Wang Weiwei, Cao Dongbo, et al. Ensemble chaotic forecasting method in short term load forecasting[J].Automation of Electric Power Systems,2007,31(23):34-37.

[8]Willis H L, Northcote-Green J E D. Spatial electric load forecasting: a tutorial review[J]. Proceedings of the IEEE, 1983, 71(2): 232-253.

[9]雷绍兰，孙才新，周湶，等．基于径向基神经网络和自适应神经模糊系统的电力短期负荷预测方法[J]．中国电机工程学报,2005,25(22):78-82. Lei Shaolan, Sun Caixin, Zhou Quan, et al. Short-term load forecasting method based on rbf neural network and anfis system[J]. Proceedings of the CSEE,2005,25(22):78-82.

[10]Amjady N, Keynia F, Zareipour H. Short-term load forecast of microgrids by a new bilevel prediction strategy[J]. IEEE Transactions on Smart Grid, 2010, 1(3): 286-294.

[11]曾鸣，吕春泉，田廓，等．基于细菌群落趋药性优化的最小二乘支持向量机短期负荷预测方法[J]. 中国电机工程学报,2011,31(34) :93-99． Zeng Ming, Lu Chunquan, Tian Kuo, et al. Least squares-support vector machine load forecasting approach optimized by bacterial colony chemotaxis method[J]. Proceedings of the CSEE,2011,31(34) :93-99．[12]Du Xinhui, Tian Feng, Tan Shaoqiong. Study of power system short-term load forecast based on artificial neural network and genetic algorithm[C]//2010 International Conference on Computational Aspects of Social Networks (CASoN). IEEE, 2010: 725-728.

[13]冯丽，邱家驹．基于模糊多目标遗传优化算法的节假日电力负荷预测[J]．中国电机工程学报,2005,25(10):29-34. Feng Li, Qiu Jiaju. Short-term load forecasting for anomalous days based on fuzzy multi-objective genetic optimization algorithm[J].Proceedings of the CSEE,2005,25(10):29-34.

[14]姜勇．南京地区春节负荷特性分析及其预测方法[J]．电网技术,2003,27(5):72-74. Jiang Yong. Load characteristics analysis and load forecasting during spring festival in nanjing district[J]. Power System Technology,2003,27(5):72-74.

[15]丁恰，张辉，张君毅，等．考虑气象信息的节假日负荷预测[J]．电力系统自动化，2005，29(17)：93-97． Ding Qia, Zhang Hui, Zhang Junyi. Temperature sensitive method for short term load forecasting during holidays[J].Automation of Electric Power Systems,2005,29(17):93-97.

[16]韩民晓，姚属军．短期负荷预测方法的研究及在线应用[J]．电力系统自动化，1998，22(10)：34-37. Han Minxiao，Yao Shujun．The research and on-line application of power system short-term load forecasting method[J]．Automation of Electric Power Systems，1998，22(10)：34-37.

[17]马文晓，白晓民，沐连顺．基于人工神经网络和模糊推理的短期负荷预测方法[J]．电网技术，2003，27(5)：29-32. Ma Wenxiao, Bai Xiaomin, Mu Lianshun. Short term load forecasting using artificial neuron network and fuzzy inference[J]. Power System Technology,2003,27(5):29-32.

[18]史文博，王健，沈添福，等．基于改进倍比平滑法的节假日短期负荷预测方法[J]．电力建设,2014,35(10)：21-25. Shi Wenbo, Wang Jian, Sheng Tianfu, et al. Prediction method of short-term load in holidays based on improved multiple proportions smoothing method [J].Electric Power Construction,2014,35(10)：21-25.

[19]毛李帆，姚建刚，金永顺，等．中长期负荷预测的异常数据辨识与缺失数据处理[J]. 电网技术，2010，34(7)：148-153． Mao Lifan，Yao Jiangang，Jin Yongshun，et al．Abnormal data identification and missing data filling in medium and long-term load forecasting[J]. Power System Technology，2010，34(7)：148-153．[20]康重庆，夏清，刘梅．电力系统负荷预测[M]．北京：中国电力出版社，2007：140，252-254．

(编辑：张媛媛)

Holiday Load Forecasting Model Considering Related Factor with Unified Correction

MIAO Jianqiang, TONG Xing, KANG Chongqing

(State Key Lab of Control and Simulation of Power Systems and Generation Equipments (Department of Electrical Engineering, Tsinghua University), Beijing 100084, China)

The energy internet is gradually impacting the planning and construction way of power grid, which puts harder request on the prediction technology of related factors. Due to the huge differences between holidays and weekdays and the lack of historic data, the results of load prediction for holidays are not so good. Weather, date and other related factors were corrected by the unified correction model of related factor, and then the data for normal weekdays impacted by unified related factors was obtained. Considering the principle of ‘emphasizing the near and belittling the long’, the relevance of load curves between normal weekdays and holidays was analyzed, and the load forecasting model was proposed based on the point-to-point analogy, which could reduce the prediction error caused by the abnormal historic data automatically. The proposed prediction method was applied to the holiday load forecasting in one of the northern cities and districts in China. The example analysis results show that the prediction accuracy can satisfy the actual requirements, which can provide a certain reference value for the holiday load forecasting of related power sector.

load forecasting; holiday; related factor; point-to-point analogy

国家电网公司科技项目(SGHB0000KXJS1400044,新形势下电力需求及售电市场分析预测技术研究)。

TM 715

A

1000-7229(2015)10-0099-06

10.3969/j.issn.1000-7229.2015.10.015

2015-06-29

2015-07-28

苗键强(1992)，男，硕士研究生，研究方向为能源互联网、负荷预测；

童星(1989)，男，博士研究生，IEEE学 生 会 员 ， 研究方向为负荷预测；

康重庆(1969)，男，教授，研究方向为低碳电力、负荷预测、电力规划等。