计及可用输电能力的含大规模风电的输电系统规划

2015-03-11郑静文福拴周明磊徐谦梁樑俞敏

电力建设 2015年10期

郑静, 文福拴, 周明磊, 徐谦, 梁樑, 俞敏

(1. 国网浙江省电力公司信通分公司,杭州市 310027; 2. 浙江大学电气工程学院,杭州市 310027;3. 文莱科技大学电机与电子工程系, 斯里巴加湾市 BE1410;4. 国网浙江省电力公司经济技术研究院, 杭州市 310008)

郑静1,2, 文福拴2,3, 周明磊1, 徐谦4, 梁樑4, 俞敏4

大容量风力发电基地的快速发展给电力系统安全与经济运行带来了新的问题，对输电系统进行规划时，既要考虑具备足够的可用输电能力(available transfer capability, ATC)以容纳大规模风电并网, 又要避免输电容量过分冗余造成投资浪费。在此背景下, 针对含有大容量风力发电的电力系统, 提出了一种计及ATC的输电系统规划随机优化模型, 主要内容包括:(1)在考虑风速和负荷等随机变量之间相关性以及线路和发电机故障概率的基础上, 构造了ATC概率模型;(2)采用拉丁超立方采样和灵敏度分析相结合的方法求解ATC概率模型;(3)构建以输电线路投资成本最小和ATC期望值最大为目标的优化模型, 将输电系统规划的经济性和运行风险进行有机结合。采用遗传算法求解所建立的输电系统规划优化模型, 并用18节点和46节点算例系统说明所发展模型和方法的基本特征。

输电系统规划; 风电场; 可用输电能力(ATC); 拉丁超立方采样; 灵敏度分析; 相关性

0 引言

在过去的10多年间, 风力发电在很多国家得到快速发展。在我国, 几个千万kW级的风电基地正在建设或已投产。随着越来越多的大规模风电场并入电力系统, 风电出力的间歇性和不确定性给系统规划和运行带来了一些新问题，就输电系统规划而言, 对规划方案的鲁棒性和灵活性要求更高,以适应数量更多、程度更强的不确定性因素[1-5]。可用输电能力(available transfer capability， ATC)在相当程度上可以反映系统运行的鲁棒性和灵活性。

ATC是指在现有的输电合同基础上, 输电网络中剩余的，可用于商业使用的输电能力[6]。ATC本质上是一种表示输电系统充裕度的指标, 通常作为运行参数。如果能够在系统规划阶段就适当考虑ATC, 则规划出来的输电系统具有更高的鲁棒性和灵活性, 能够更好地适应含有大规模风电场的电力系统的安全与经济运行。

含大规模风电的电力网络规划问题在最近几年受到了比较多的关注, 国内外已有一些研究报道[1-8]。在文献[3]中, 把风电出力不确定性用一些代表性的场景和相关概率来表示, 在输电规划问题的目标函数中考虑多种情况下线路过负荷的惩罚成本, 使得到的规划方案满足投资经济性和运行可靠性的要求。文献[4-5]提出了计及负荷和风电场输出功率不确定性的输电系统规划方法, 将过负荷概率控制在一定的置信度水平, 兼顾了输电系统规划的经济性和可靠性。文献[7]提出了综合考虑经济性和接纳间歇性可再生能源发电能力的输电系统规划方法。文献[8-9]构建了考虑风电场接入规划和电力网络规划的联合规划模型, 综合考虑了投资经济性、系统可靠性和环境效益等多方面整体最优。上述文献都是在目标函数中计入过负荷惩罚成本或者将过负荷水平作为约束条件来保证规划方案的可靠性水平和系统运行的安全性。如果能够在输电系统规划中适当考虑系统的ATC, 则所得到的规划方案不仅可以满足线路不过负荷的安全性要求, 也具有更高的鲁棒性和灵活性, 能更好地适应风电所带来的不确定性, 且与电力工业市场化的趋势相适应。

在上述背景下, 针对含大规模风电的电力系统, 本文将建立计及ATC的输电系统规划随机优化模型。首先, 在考虑风速和负荷等随机变量之间相关性以及线路和发电机故障概率的基础上, 构造ATC概率模型, 并采用拉丁超立方采样(latin hypercube sampling, LHS)和灵敏度分析相结合的方法进行求解。以输电线路投资成本最小和ATC期望值最大为目标函数、允许的线路过负荷概率等为约束条件, 建立输电系统多目标规划模型, 然后转化为单目标优化问题并采用遗传算法进行求解。最后, 采用2个算例系统对所提模型和求解方法进行分析。

1 概率ATC计算

大规模风电接入电力系统后, 风电出力的不确定性会对系统的ATC产生影响, 目前已有一些文献评估了这种影响[10-13]。现有ATC计算模型包括确定性的和概率的[14], 其中概率模型能有效计及随机因素对ATC的影响。概率ATC计算是利用概率理论和数理统计分析方法确定系统可用输电能力的过程。针对电力系统所具有的随机特征, 通过随机变量的状态模拟系统可能出现的运行场景, 然后采用合适的优化方法求解这些场景下的ATC, 最后采用统计分析得到ATC概率分布或期望值与方差等。

概率ATC计算包括系统运行状态模拟和确定性ATC计算2部分。这里采用LHS法[15-16]和灵敏度分析[17]相结合的方法,计及随机变量之间的相关性以及线路和发电机故障概率,求解风电并网环境下系统的概率ATC。首先采用LHS对输入随机变量进行抽样, 然后根据相关性关系进行排序, 得到最终的采样场景集合。对于LHS采样得到的每个场景, 采用灵敏度分析法计算其ATC, 最终通过统计方法得到ATC的概率分布和统计特性参数如期望值和方差等。

1.1 考虑随机变量相关性的LHS

1.1.1 LHS

LHS是一种分层采样方法, 可以利用采样值反映随机变量的整体分布, 已在多个领域得到应用[15]。与传统的随机采样相比, 在相同的采样规模下, LHS的采样空间大, 稳健性好, 精度高, 速度快。

LHS主要包括采样和排序2个主要步骤。在采样阶段, 需确保采样点涵盖输入随机变量的分布区域; 排序阶段则通过改变各随机变量采样值的排列顺序, 使随机变量采样值的相关性满足相关要求。

(1)采样。假设x1,x2, …,xn为待求解问题中的n个输入随机变量, 且任一随机变量xk的概率分布函数为

uk=Fk(xk),k=1,2,…,n

(1)

(2)排序。随机变量采样值之间的相关性会影响LHS的计算精度, 改变各随机变量采样值的排列顺序, 可以使相互独立的随机变量的采样值的相关性趋于最小; 而对于随机变量具有相关性的情况, 改变采样值的排列顺序, 也可以使随机变量采样值的相关性更加接近实际情况。排序方法有多种, 如Gram-Schmidt序列正交化方法[15]、Cholesky分解法[18]等。在排列过程中形成一个n×N阶的顺序矩阵S, 该矩阵的每行元素值表示采样矩阵X对应行的元素应该排列的位置。X的元素按照顺序矩阵S排列后形成最终的采样矩阵。

1.1.2 随机变量相关性的处理

假设x1,x2,…,xn的相关系数矩阵为Rx, 且Rx为正定矩阵:

(2)

(3)

式中:ρij为变量xi和xj的相关系数; cov(xi,xj)为xi和xj的协方差;σi和σj分别为xi和xj的标准差。

引入标准正态分布的随机变量y1,y2, …,yn, 其满足:

yk=Φ-1[Fk(xk)]，k=1,2,…,n

(4)

式中Φ为标准正态分布的概率分布函数。

假设y1,y2, …,yn的相关系数矩阵为Ry:

(5)

Rx和Ry的非对角线元素满足:

(6)

式中:G(ρij)与xi和xj的概率分布有关。例如, 当xi和xj服从正态分布时,G(ρij)=1; 当xi和xj服从Weibull分布时,G(ρij)可近似表示为[16]

(7)

式中:γi=σi/μi;γj=σj/μj;μ和σ分别对应随机变量x的均值和标准差。当xi和xj服从其他分布时, 可采用文献[16]的方法求取G。

对Ry进行Cholesky分解, 可得到下三角矩阵L。对随机变量y1,y2, …,yn进行采样, 得到样本矩阵Wn×N; 然后, 由Y=LW得到相关系数矩阵为RY的样本矩阵[16], 进而得到其顺序矩阵S。由于Φ和F-1都是单调递增函数, 因此样本矩阵X的顺序矩阵与样本矩阵Y的顺序矩阵相同, 即同为S。将样本矩阵X按照顺序矩阵S进行排序, 可得到最终的考虑随机变量相关性的样本矩阵H。

1.2 灵敏度分析

针对不同的需求, 可采用不同的方法计算ATC, 如灵敏度分析法[17]、最优潮流法[19]等。灵敏度分析法计算速度快, 可计及输电设备过负荷约束和“N-1”静态安全约束, 其计算精度也能满足输电系统规划要求。

直流潮流模型的一般形式为

P=Bθ

(8)

支路潮流可描述为

pij=bij(θi-θj)=bijeijθ

(9)

将式(8)代入式(9)可得:

pij=bijeijB-1P

(10)

式中:P为节点注入功率向量;B为系统节点导纳矩阵;θ为节点电压相角向量;bij为支路ij的电纳值;pij为支路ij的有功功率;eij为支路ij对应的节点关联行向量, 除i和j列元素分别为+1和-1外, 其余元素均为0;θi和θj分别为节点i和节点j的电压相角。

用功率传输分配因子(PTDF)[17]表征送、受端间增加单位有功功率时各支路潮流的变化:

Sij=bijeijB-1β

(11)

每条支路ij都有一个最大功率传输能力Tij。Tij最小的支路即是影响ATC的瓶颈支路, 此支路对应的Tij即为当前状态下系统的ATC[17]:

(12)

(13)

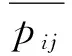
1.3 考虑随机变量相关性的概率ATC计算

对于有大规模风电接入的电力系统, 计算ATC时需要考虑相关的不确定性, 这可以描述为概率ATC计算问题。这里的概率ATC计算主要考虑3种不确定性因素: (1) 发电机和输电线路随机故障, 假设均服从两点分布; (2) 节点负荷随机波动, 假设均服从正态分布; (3)风电场的风速随机变化, 假设服从Weibull分布。

虽然单个风电场的风速具有很强的随机性, 但不同风电场间的风速序列未必完全独立, 即可能存在相关性。不同风电场间的风速相关性主要与风电场之间的地理距离有关, 相距较近的风电场的风速往往表现出较强的相关性, 较远的则相关性较弱。系统负荷与气候之间也存在一定的相关性。风速与负荷之间的相关性较弱[20], 可近似认为二者相互独立。这些相关性会影响潮流和ATC计算。本文在计算ATC时考虑了不同风电场风速之间以及系统负荷之间的相关性。采用LHS和灵敏度分析法计算ATC的步骤如下。

(1) 发电机组状态采样。按照发电机组的两点分布对其状态进行采样, 对于电源和负荷之间的功率差值 (即不平衡量), 按运行机组的额定功率比例进行分配。

(2) 风电场出力采样。根据风速的概率密度函数以及相关系数矩阵Rw, 由1.1节的LHS法采样得到考虑相关性的风速样本矩阵Hw; 然后, 根据风电场出力和风速的关系[5], 由样本矩阵Hw得到风电场出力的样本矩阵Hwp。

(3) 输电线路状态采样。按照输电线路的两点分布对其状态进行采样, 如果在某种抽样结果情况下系统不能满足安全要求, 如出现孤岛, 则认为这种状态下的ATC为0。

(4) 负荷采样。根据负荷的概率密度函数以及相关系数矩阵Rl, 由1.1节的LHS法采样得到考虑相关性的负荷样本矩阵Hl。

(5) 潮流计算。根据Hwp和Hl, 对采样得到的每个场景进行潮流计算; 如果出现支路过负荷, 则认为该场景的ATC为0。

(6) ATC计算。根据1.2节的灵敏度分析法计算每个场景下的系统ATC。

(7) ATC概率分布。循环执行步骤(1)～(6), 计算得到N个场景下的ATC后, 可以采用统计分析方法得到ATC的概率分布, 同时也可获得线路过负荷的概率分布。

(8) 计算N个场景下ATC的期望值EATC:

(14)

2 输电系统规划模型

在对含有大容量风力发电的电力系统进行输电系统规划时, 由于风电出力波动性较大, 如果要保证所有的线路在任何情况下都不过负荷, 有可能造成输电容量过度配置, 从而降低输电系统的投资和运行效益。可以设置一定的阈值, 将线路过负荷概率控制在允许范围内。另一方面, 输电系统规划需要留有足够的可用输电能力, 以应对风电出力不确定性所带来的运行安全风险。基于上述考虑, 这里以最小化输电投资成本和最大化可用输电能力期望值作为2个优化目标:

(15)

f2: maxW=EATC

(16)

式中:Cl为支路l的单回线路造价，万元/km,;Zl为支路l的扩建线路数;W为规划方案对应的ATC期望值。

采用多目标优化方法中的乘除法对目标函数f1和f2进行合并处理, 即以W/C作为目标函数。W/C的含义为单位投资所对应的系统可用输电容量期望值。这样, 计及ATC的输电系统规划问题可描述如下:

(17)

s.t.

Bθ=PW+PG-PL

(18)

(19)

(20)

(21)

(22)

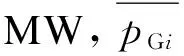
采用遗传算法[21]对上述优化模型进行求解。采用适应度函数对候选规划方案进行优劣评价, 以此控制搜索方向。优化过程通过选择、交换、变异等措施进行, 逐步收敛到最优解。关于遗传算法的具体求解过程, 这里不赘述, 见文献[21]。

3 算例分析

下面用18节点系统[22]和46节点系统[23]来说明所提输电系统规划模型的可行性与有效性。采用正态分布描述这2个系统在规划水平年各负荷节点的负荷需求, 取这2个系统中原有的负荷需求数据为相应的期望值, 均方差取为期望值的4%，采用这种方式来描述未来负荷需求的不确定性。

假定每回线路的单位投资成本为200万元/km, 每年每回线路单位长度的停运率为0.05次/km, 线路修复率为9.13×10-4年/(次回)[24], 发电机组的故障率为1%, 支路潮流不越限的概率下限值给定为0.9。

3.1 18节点系统

该系统现有10个节点, 9条线路 (见附录的图A1)。在未来某规划水平年, 系统增加为18个节点, 包括7个电源节点, 17个负荷节点, 总负荷期望值为35 870 MW, 其中节点11、14、16、18为新增发电机节点。发电机容量和负荷功率见附表A1, 每条候选走廊最大可扩建3条线路。关于该系统更详细的数据和说明可参见文献[22]。假定节点2连接2个装机容量均为4 680 MW的风电场, 风电总装机容量占整个系统装机容量的18.24%。假定2个风电场的风机特性相同, 切入、切出、额定风速分别为3.00,，22.00，10.00 m/s; Weibull分布中的参数取值为:c=6.5,k=3。2个风电场风速的相关系数为0.7, 系统负荷之间的相关系数为0.8。

这里针对下述3种情况重点评估考虑ATC和风速相关性时对输电系统规划的影响。

(1)考虑ATC时对输电系统规划的影响。采用上述方法可获得3个较优的规划方案, 如表1所示。其中, 新建线路一栏括号内的数字表示需新增回路数, 如1(2)表示支路1新增2回线, 其余类同。

由表1可知, 方案A的输电投资成本比方案C高出1.23%, 但方案A的ATC期望值比方案C高出7.98%, 则方案A的目标值大于方案C。方案B的投资费用最高, 比方案A高出4.08%, 但其ATC期望值只比方案A高出2.17%, 这表明方案B的高投资并没有带来期望的高ATC值。方案A的目标函数值最大, 综合效益在3个方案中最优。

(2)风速相关性对输电系统规划的影响。改变风电场风速之间的相关性, 取风速独立和完全相关2种情况, 求解规划模型得到规划方案D和E, 如表2所示。

表1 18节点系统三个优化规划方案比较

Table 1 Comparisons of three optimal planning schemes for the 18-bus system

表2 18节点系统在风速相关性不同时所得规划方案Table 2 Three planning schemes with different correlations of wind speed for the 18-bus system

由表2可知, 与方案A相比, 方案D输电投资和ATC期望值都小, 而方案E的输电投资和ATC期望值都大。这是因为在方案D中2个风电场的风速相互独立, 其波动的同步性较弱, 甚至可能出现“互补”, 这使得风电场总出力的波动变小, 从而使输电投资成本和ATC期望值都降低。而在方案E中, 风电场的风速之间完全相关, 使得两个风电场出力的波动性相叠加, 这增大了风电出力的峰谷差, 进而导致输电投资成本增加。

图1为方案D和E的ATC概率密度函数。当2个风电场的风速相互独立时, ATC的期望值和方差分别为4 093.46 MW和2 020.06 MW2; 当2个风电场的风速完全相关时, ATC的期望值和方差分别为5 369.69 MW和2 275.46 MW2。由图1(a)和1(b)可知, ATC在期望值附近的概率较大; ATC为0的概率也都比较大, 且图1(a)在ATC为0处的概率小于图1(b)的, 这是因为在出现过负荷的场景中将ATC置为0, 且风电场总出力的波动在风速相互独立时较风速完全相关时小。

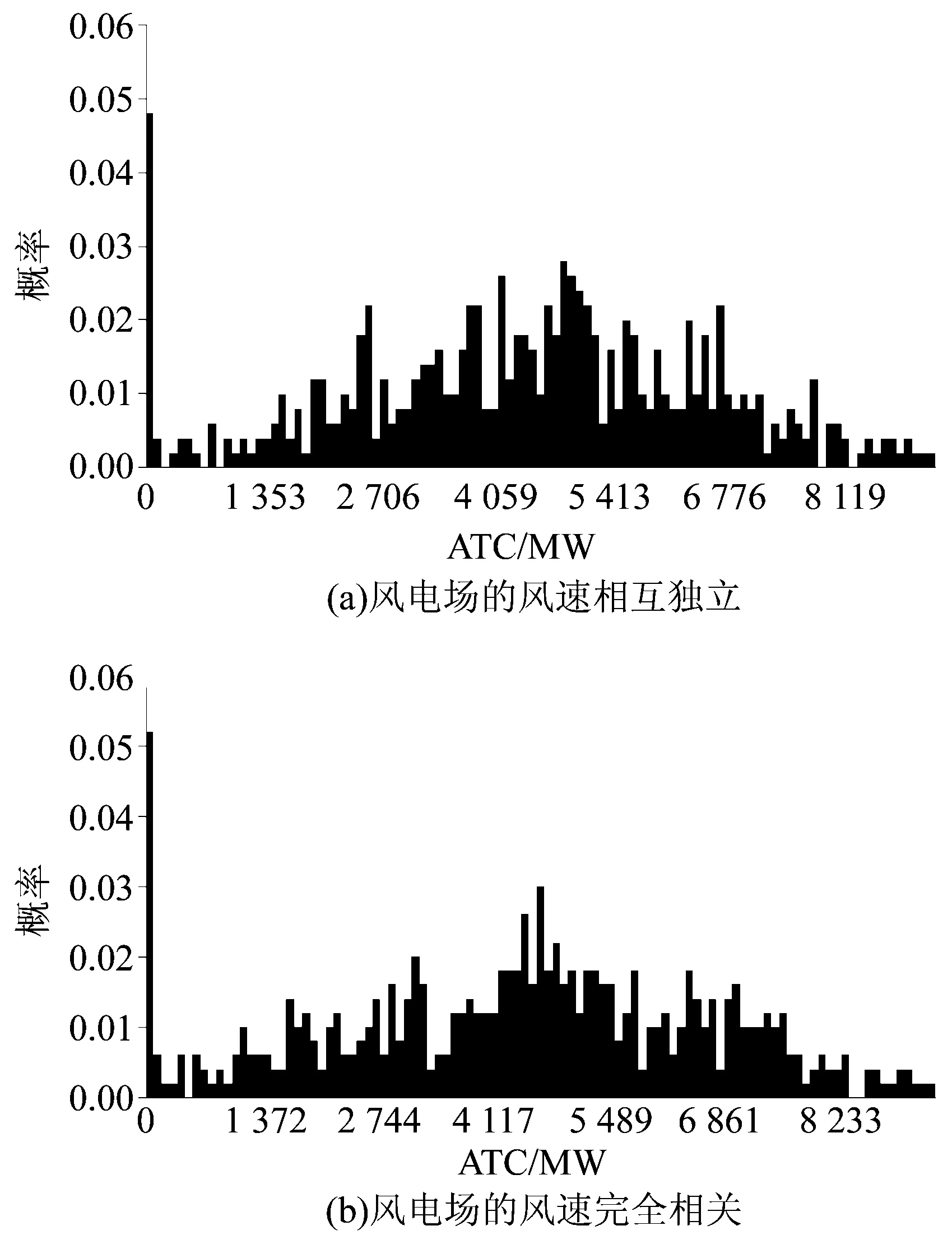
图1 ATC概率密度分布Fig.1 The probability density of ATC for planning scheme

(3)风电场的接入方式对输电系统规划的影响。保持风速相关系数为0.7, 将其中一个风电场接到节点11, 重新进行规划, 得到优化方案F, 与优化方案A的比较如表3所示。

由表3可知, 与方案A相比, 方案F的投资成本更小, 而ATC期望值则远大于方案A, 这使得方案F的投资效益远大于方案A。这是由于在方案F中2个风电场接在不同的节点上, 使得风电波动性的叠加效果比方案A弱, 从而减少了对系统潮流的影响, 所需的输电投资减少了, 而ATC期望值增大了, 这导致输电投资效益大大提高。

3.2 46节点系统

该系统为巴西南部电网, 现有35个节点, 62条线路(见附录的图A2)。在未来某规划水平年, 系统增加为46个节点, 包括12个电源节点, 19个负荷节点, 总负荷期望值为6 880 MW, 其中节点16、28、31为新增发电机节点。发电机容量和负荷功率见附表A2。关于该系统更详细的数据和说明可参见文献[23]。假定节点17连接2个规格相同、装机容量均为750 MW的风电场, 风电机组装机容量占系统总装机容量的16.4%, 风电场的参数与18节点系统算例相同。计算输电投资时, 以1美元兑换6.5元人民币的汇率折算。采用所提方法可得到3个规划方案, 如表4所示。

由表4可知, 与表1的18节点系统规划结果类似, 方案H的输电投资成本和ATC期望值都介于方案J和方案K之间, 但是其目标函数值最大, 为投资效益最高的规划方案。

改变2个风电场风速的相关性, 相关系数在区间[0,1]内依次取值, 用所提出的方法进行规划, 得到相应最优规划方案的目标函数值曲线, 如图2所示。

表3 在不同的风电场接入方式下获得的18节点系统规划方案

Table 3 Planning schemes with different connection modes of wind farms for the 18-bus system

表4 46节点系统3个规划方案比较Table 4 Comparisons of three planning schemes for the 46-bus system

图2 在不同风速相关性时得到的最优规划方案的目标函数值Fig.2 The objective function values of optimal planning schemes under different wind speed correlations

由图2可知, 对于46节点系统, 考虑风速相关性时获得的最优规划方案的综合效益比假设风速独立时要大, 这主要是因为风速相互独立的2个风电场波动的同步性较弱, 风电出力的叠加效果较小, 从而使输电投资成本和ATC期望值都较小; 由于ATC期望值减小的幅度比输电投资成本减小的幅度小, 这导致假设风速独立的情况比考虑风速相关性时所得到的最优规划方案的综合效益差一些。此外, 通过对其他算例系统进行仿真, 发现不同系统的最优规划方案的综合效益与风速相关性的变化关系曲线不尽相同, 并不一定在相关性为0.5时达到最佳值。综合效益与风速相关性的变化关系曲线受网络结构、风电场规模及风电场接入点等多个因素的影响。

4 结语

针对含有大规模风电接入的电力系统, 本文构造了一种计及ATC的输电系统规划随机优化模型。通过对2个算例系统的分析表明，风速的相关性和风电场的接入方式会对输电投资成本和ATC产生影响, 因此在输电规划决策时需要在输电投资经济性和系统运行风险之间进行折衷, 使输电规划方案的综合效益最佳。但是，本文的研究工作还相当初步, 尚有一些因素没有考虑, 如系统的运行成本和风电场集群效应等, 这些问题有待进一步深入研究。

[1]周金辉, 余贻鑫, 曾沅. 大规模风电接入下输电网扩展规划的启发式优化算法[J]. 电力系统自动化, 2011, 35(22): 66-70. Zhou Jinhui, Yu Yixin, Zeng Yuan. Heuristic optimization algorithm for transmission network expansion planning with large-scale wind power integration[J]. Automation of Electric Power Systems, 2011, 35(22): 66-70.

[2]彭波, 陈旭, 徐乾耀, 等. 面向新能源消纳的电网规划方法初探[J]. 电网技术, 2013, 37(12): 2286-3391. Peng Bo, Chen Xu, Xu Qianyao, et al. Preliminary research on power grid planning method aiming at accommodating new energy[J]. Power System Technology, 2013, 37(12): 2286-3391.

[3]袁越, 吴博文, 李振杰, 等. 基于多场景概率的含大型风电场的输电网柔性规划[J]. 电力自动化设备, 2009, 29(10): 8-12. Yuan Yue, Wu Bowen, Li Zhenjie, et al. Flexible planning of transmission system with large wind farm based on multi-scenario probability[J]. Electric Power Automation Equipment, 2009, 29(10): 8-12.

[4]于晗, 钟志勇, 黄杰波, 等. 考虑负荷和风电出力不确定性的输电系统机会约束规划[J]. 电力系统自动化, 2009, 33(2): 20-24. Yu Han, Chung C Y, WONG K P, et al. A chance constrained transmission network expansion planning method associated with load and wind farm variation[J]. Automation of Electric Power Systems, 2009, 33(2): 20-24.

[5]郑静, 文福拴, 李力, 等. 计及风险控制策略的含风电机组的输电系统规划[J]. 电力系统自动化, 2011, 35(22): 71-76. Zheng Jing, Wen Fushuan, Li Li, et al. Transmission system planning with risk-control strategies for power systems with wind generators[J]. Automation of Electric Power Systems, 2011, 35(22): 71-76. [6]North American Electric Reliability Council (NERC). Available transfer capability definition and determination[EB/OL], 1996. Available at http://www.westgov.org/wieb/wind/06-96NERCatc.pdf.

[7]黄裕春, 杨甲甲, 文福拴, 等. 计及接纳间歇性电源能力的输电系统规划方法[J]. 电力系统自动化, 2013, 37(4): 28-34. Huang Yuchun, Yang Jiajia, Wen Fushuan, et al. Transmission system planning considering capability of accommodating intermittent generation sources[J]. Automation of Electric Power Systems, 2013, 37(4): 28-34.

[8]王茜, 张粒子. 采用NSGA-II混合智能算法的风电场多目标电网规划[J]. 中国电机工程学报, 2011, 31(19): 17-24. Wang Qian, Zhang Lizi. Multi-objective transmission planning associated with wind farms applying NSGA-II hybrid intelligent algorithm[J]. Proceedings of the CSEE, 2011, 31(19) :17-24.

[9]吕冰, 颜伟, 赵霞, 等. 考虑能量随机性的分布式风电和联络线协调规划[J]. 中国电机工程学报, 2013, 33(34): 145-152. Lu Bing, Yan Wei, Zhao Xia, et al. Corrdinated allocation of tie lines and DWGs considering random energy[J]. Proceedings of the CSEE, 2013, 33(34): 145-152.

[10]周明, 冉瑞江, 李庚银. 风电并网系统可用输电能力的评估[J]. 中国电机工程学报, 2010, 33(22): 14-21. Zhou Ming, Ran Ruijiang, LI Gengyin. Assessment of available transfer capacity of wind farm incorporated system[J]. Proceeding of the CSEE, 2010, 33(22): 14-21.

[11]王成山, 王兴刚, 孙玮. 含大型风电场的电力系统概率最大输电能力快速计算[J]. 中国电机工程学报, 2008, 28(10): 56-62. Wang Chengshan, Wu Xinggang, Sun Wei. Fast calculation and analysis of probabilistic total transfer capability in power system including large-scale wind farms[J]. Proceeding of the CSEE, 2008, 28(10): 56-62.

[12]王成山, 孙玮, 王兴刚. 含大型风电场的电力系统最大输电能力计算[J]. 电力系统自动化, 2007, 31(2): 17-21. Wang Chengshan, Sun Wei, Wang Xinggang. Total transfer capability calculation of power system including large-scale wind farm[J]. Automation of Electric Power Systems, 2007, 31(2): 17-21.

[13]杨燕, 文福拴, 李力, 等. 计及风险控制策略的电力系统可用输电容量决策[J]. 电力系统自动化, 2012, 36(4): 50-55. Yang Yan, Wen Fushuan, Li Li, et al. Available transfer capability decision-making with risk-control strategies[J]. Automation of Electric Power Systems, 2012, 36(4): 50-55.

[14]崔雅莉, 别朝红, 王锡凡. 输电系统可用输电能力的概率模型及计算[J]. 电力系统自动化, 2003, 27(14): 36-40. Cui Yali, Bie Zhaohong, Wang Xifan. Study on probabilistic models and algorithms of available transfer capability[J]. Automation of Electric Power Systems, 2003, 27(14): 36-40.

[15]于晗, 钟志勇, 黄杰波, 等. 采用拉丁超立方采样的电力系统概率潮流计算方法[J]. 电力系统自动化, 2009, 33(21): 32-35. Yu Han, Chung Chiyong, Wong Kitpo, et al. A probabilistic load flow calculation method with Latin hypercube sampling[J]. Automation of Electric Power Systems, 2009, 33(21): 32-35.

[16]陈雁, 文劲宇, 程时杰. 考虑输入变量相关性的概率潮流计算方法[J]. 中国电机工程学报, 2011, 31(22): 80-87. Chen Yan, Wen Jinyu, Cheng Shijie. Probabilistic load flow analysis considering dependencies among input random variables[J]. Proceeding of the CSEE, 2011, 31(22): 80-87.

[17]Ejebe C G, Waight J G, Manuel S N, et al. Fast calculation of linear available transfer capability[J]. IEEE Transaction on Power Systems, 2000, 15(3): 1112-1116.

[18]Yu H，Chung C Y, Wong K P, et al. Probabilistic load flow evaluation with hybrid Latin hypercube sampling and Cholesky decomposition[J]. IEEE Transaction on Power Systems, 2009, 24(2): 661-667.

[19]汪峰, 白晓民. 基于最优潮流方法的传输容量计算研究[J]. 中国电机工程学报, 2002, 22(11): 35-40. Wang Feng, Bai Xiaomin. OPF based transfer capability calculation[J]. Proceedings of the CSEE, 2002, 22(11): 35-40.

[20]George P, Dorota K. Using copulas for modeling stochastic dependence in power system uncertainty analysis[J]. IEEE Transaction on Power Systems, 2009, 24(1): 40-49.

[21]Da Silva E L, Gil H A, Areiza J M. Transmission network expansion planning under an improved genetic algorithm[J]. IEEE Transaction on Power Systems, 2000, 15(3): 1168-1174.

[22]王锡凡. 电力系统优化规划[M]. 北京: 水利电力出版社, 1990.

[23]Romero R, Monticelli A, Garcia A, et al. Test systems and mathematical models for transmission network expansion planning[J]. IEEE Proceedings: Generation, Transmission and Distribution, 2002, 149(1): 27-36.

[24]程浩忠, 高赐威, 马则良, 等. 多目标电网规划的分层最优化方法[J]. 中国电机工程学报, 2003, 23(10): 11-16. Cheng Haozhong , Gao Ciwei, Ma Zeliang, et al. The lexicographically stratified method for mutli-object optimal electric power network planning[J]. Proceedings of the CSEE, 2003, 23(10): 11-16.

郑静 (1980), 女, 博士, 工程师, 主要从事电力系统规划和可再生能源方面的研究工作；

文福拴 (1965), 男, 通信作者, 教授, 博士生导师, 主要从事电力系统故障诊断与系统恢复、电力经济与电力市场、智能电网与电动汽车等方面的研究工作；

周明磊 (1974), 男, 硕士, 高级工程师, 主要从事电力信息化管理工作；

徐谦 (1963), 男, 硕士, 高级工程师，主要从事电力系统规划研究及咨询工作；

梁樑 (1981), 男, 硕士, 工程师, 主要从事电网工程技术经济研究方面的工作；

俞敏 (1968), 女, 硕士, 高级工程师, 主要从事电网工程技术经济研究方面的工作。

(编辑：张小飞)

附录

表A1 18节点系统节点参数

Table A1 Bus data of the 18-bus system

Transmission System Planning in Power Systems with Wind Generators Considering Available Transfer Capability

ZHENG Jing1,2, WEN Fushuan2,3, ZHOU Minglei1, XU Qian4, LIANG Liang4, YU Min4

(1. Information and Communication Division, State Grid Zhejiang Electric Power Corporation, Hangzhou 310027, China;2. School of Electrical Engineering, Zhejiang University, Hangzhou 310027, China;3. Department of Electrical and Electronic Engineering, Institut Teknologi Brunei, Bandar Seri Begawan BE1410, Brunei;4. State Grid Zhejiang Electric Power Corporation Economic Research institute, Hangzhou 310008, China)

The rapid development of large-scale wind farms results in some new problems for the secure and economic operation of the power system associated. In making transmission system planning, sufficient available transfer capability (ATC) is required so as to accommodate large-scale wind farms, while excessive transmission capacity must be avoided so as to save investment. Given this background, a stochastic optimization model for transmission system planning is presented for a power system with the integration of large-scale wind farms with the following contributions: 1) a probabilistic ATC model is developed with the correlations among random input variables such as wind speed and loads as well as the outage probabilities of generators and transmission lines taken into account; 2) a method is employed to solve the probabilistic ATC model by the combined use of the Latin hypercube sampling based Monte Carlo simulation and sensitivity analysis; 3) a bi-objective transmission system planning model is presented with transmission investment cost minimized and the expected value of ATC maximized, subject to the acceptable overload probability constraints, and in this way the economics and operation risks associated with a transmission planning scheme could be compromised. Finally, the developed transmission system planning model is solved by the well-established genetic algorithm, and demonstrated by a 18-bus and a 46-bus sample power systems.

transmission system planning; wind farm; available transfer capability (ATC); Latin hypercube sampling; sensitivity analysis; correlation

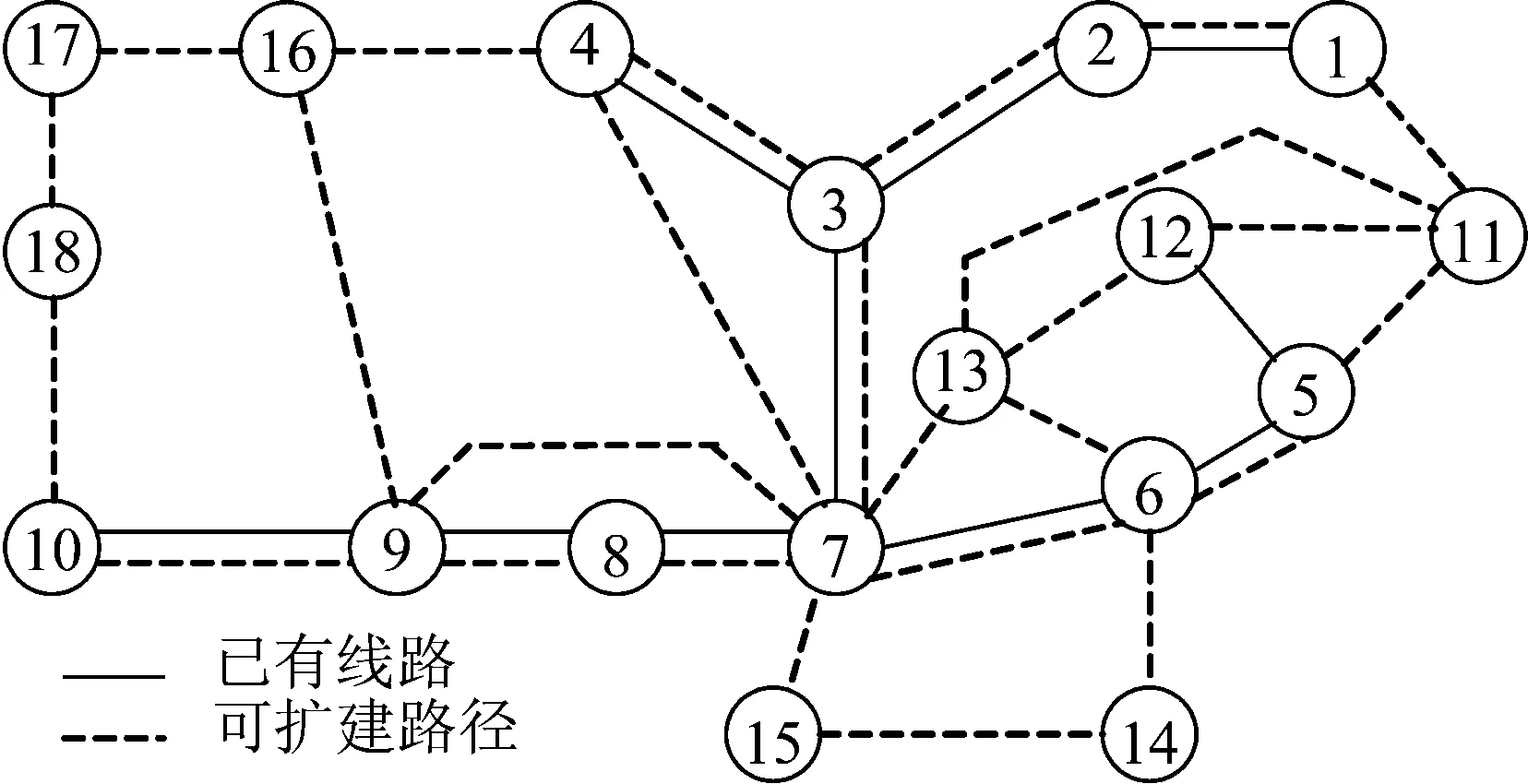
图A1 18节点系统图Fig.A1 The 18-bus system

图A2 46节点系统图Fig.A2 The 46-bus system表A2 46节点系统节点参数Table A2 Bus data of the 46-bus system

国家重点基础研究发展规划项目 (973计划) (2013CB228202); 国家自然科学基金项目 (51477151, 51361130152); 国网浙江省电力公司科技项目(5211DS14000X)。

TM 715

1000-7229(2015)10-0073-09

10.3969/j.issn.1000-7229.2015.10.011

2015-06-25

2015-08-26

Project supported by National Key Basic Research Program of China (2013CB228202); National Natural Science Foundation of China(51477151, 51361130152).