缓解中断风险的应急供应链网络鲁棒优化

卢梦飞， 陈伟炯， 梁承姬

（上海海事大学 物流研究中心，上海 201306）

随着需求和供应的不确定性增加、产品和技术生命周期的缩短、市场全球化、企业协同合作等供应链关系的日益复杂，加之工业进步和经济发展，全球变暖，世界环境日益恶化，造成各种突发灾害的频繁发生，供应链中断的风险逐步增大。2014年2月，德国安联集团发布的企业风险报告中指出：企业面对的头号风险是业务和供应链中断风险。面对中断事件企业必须及时开展应急活动，尽量保障客户需求的正常供应，减少损失。供应中断造成供应波动，仅仅依靠主要供货渠道难以迅速地满足客户需求，必须采取有效的应急策略快速修复中断供应链，供应链修复设计已经引起人们广泛关注。

突发事件中断下的供应链网络设计作为重要的战略决策对系统运作效率和效益起决定性作用。文献［1］考虑供应商失效损失、维护供应商关系成本等，建立了需求分配的优化模型；文献［2］指出期权契约具有抗突发事件性，分析了突发事件对供应链的影响并给出最优的应对策略；文献［3］以期望成本最小为目标分析了供应链中断风险下节点企业间的应急协调问题；文献［4］在供应商和客户可能失效的背景下，以总成本最小为目标进行客户的选址和客户的分配；文献［5］以期望成本（正常和中断）最小为目标建立整数规划模型，优化中断风险下设施选址、客户分配、库存管理；文献［6］研究了供应链节点失效的应急策略，建立了有限资源约束下的单目标多时段成本优化模型，得到应急调度计划和扩容策略；文献［7］提出在突发事件风险下物流系统服务中断的防御策略——加固关键物流节点和预设应急库存，建立了双层随机混合整数规划的物流系统防御模型；文献［8］权衡了网络弹性水平和期望成本建立了混合整数规划模型，得到失效风险下最优的供应网络；文献［9］运用可靠性理论构建了可靠的供应商选择模型，并结合失效相关性定量模型，得出最优供应商选择等级排序；文献［10］以供应链期望成本最小为目标建立了一个考虑响应时间和拥堵情况的混合整数规划模型，构建了随机中断下快速响应的灾后供应链。

以上对供应链网络的研究均是从需求满足率最高和经济效益最大的角度进行的，对风险下动态供应链网络设计须同时考虑解决方案的鲁棒性和可变性的鲁棒性，但目前相关研究并不多。文献［11］运用了p－鲁棒方法研究了设施中断下可靠的供应链网络设计；文献［12］研究了分销中心和运输模式同时面临随机中断的可靠供应链网络设计，建立了非线性混合整数规划模型，并引入条件风险值法进行风险控制。中断风险下的供应链恢复设计应将不同类型的应急策略考虑进鲁棒性网络设计中，但目前少有研究。本文以最小化成本为目标，建立了基于多场景、多时段的混合整数鲁棒优化模型，在协调供应和需求的同时确保网络的鲁棒性，确定不同需求场景不同时段下供应商和应急策略的选择、制造商处的库存水平、节点企业间流量等。在权衡成本和风险等条件下，研究供应链决策者的风险态度和可变性权重对网络设计的影响。

1 问题定义

1.1 供应链网络结构

本文研究包含“供应商－制造商－客户群”3层供应链网络供应中断情形下的快速恢复，网络如图1所示，主供应商S1、S2、S3与企业保持长期合作关系的，其主要优势是价格低廉；第三方备选供应商B1当中断发生后启用，其主优势是可靠性高。供应商供应原材料给制造商，制造商M具有储存、加工、分销等功能，最终将产品交付给客户群R。

文献［13］指出在一个供应网络中同时有2个或2个以上的供应商发生中断的可能性很小，可忽略不计。本文假设生产周期内突发事件仅造成1个主供应商S发生中断，中断造成的影响会沿着供应链向下游传播，最终影响客户的需求满足；为缓解中断造成的影响，本文将应急策略考虑到供应链网络设计中。应急策略主要包括期权、应急库存、备选供应商、中断供应商的修复，根据中断发生的强度对应急策略进行按需组合。

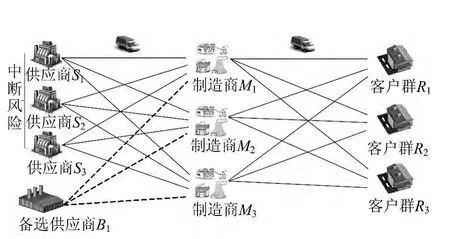
图1 供应链网络

考虑供应链网络中分布一定规模的R个客户群体、I个主供应商、J个制造商，在一定的风险态度和可变性权重下，以供应链恢复成本（包括供应商启动成本、库存成本、运输成本、采购成本、应急成本）最小为目标，确定供应中断情形下供应链网络的最优配置，并确定客户对制造商及供应商对制造商的分配，从而构建出兼具鲁棒性和经济性双重效益的3层供应链网络。

1.2 鲁棒模型介绍

文献［14］在1995年首次提出鲁棒优化概念，被认为是在不确定环境下供应链优化设计和管理的有效工具，鲁棒优化可以通过一系列场景处理风险规避和服务水平偏好。根据风险环境下供应链网络设计的特性，鲁棒优化能够缓解中断风险不确定性的影响，可以牺牲一定程度的鲁棒性从而提高优化问题的整体性能指标，在鲁棒性和最优性上做折中，因此本文将采用文献［15］提出的鲁棒模型：

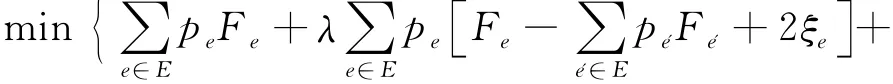
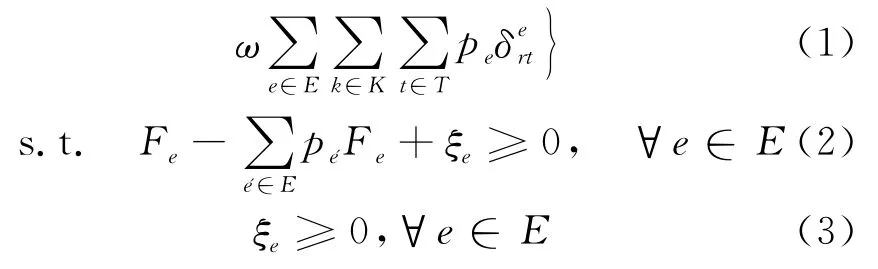
模型中主要考虑总成本与未满足需求量2个因素，进行解决方案鲁棒性与模型鲁棒性间的权衡，以得到最佳的鲁棒结果。（1）式中是衡量解决方案的鲁棒性，解决方案鲁棒性越高，任何一个场景下该方案的总成本与最优期望成本的接近程度越高。其中，可变性权重λ用于描述对成本变化幅度的接受程度，其值越大，说明决策者越希望得到成本较稳定的供应链配置；ξe为非负偏差变量，将模型转化为线性模型。是衡量模型鲁棒性，模型鲁棒性代表方案的可行性，即未满足需求量。其中，风险厌恶权重ω用于权衡解决方案鲁棒性和模型鲁棒性，例如，当ω＝0时，目标函数是最小化，此时决策者认为降低成本比降低未满足需求量（提升客户满意度）重要，因此模型的解将具有较高的解决方案鲁棒性和较低的模型鲁棒性；反之，随着ω的增大，决策者转变为风险厌恶型，决策者愿意支付较高的供应链成本达到较高的顾客满意度。（2）式、（3）式为辅助方程约束。

2 模 型

2.1 符号定义

（1）集合。S＝｛1，2，…，NI｝为供应商集合，通过i∈I索引；M＝｛1，2，…，NJ｝为制造商集合，通过j∈J索引；R＝｛1，2，…，NR｝为客户集合，通过r∈R索引；B＝｛1，2，…，NB｝为备选供应商集合，通过b∈B 索引；T＝｛1，2，…，NT｝为时间步长集合，通过t∈T 索引；E＝｛1，2，…，NE｝为场景集合，通过e∈E索引。

2.2 模型

目标函数如下：

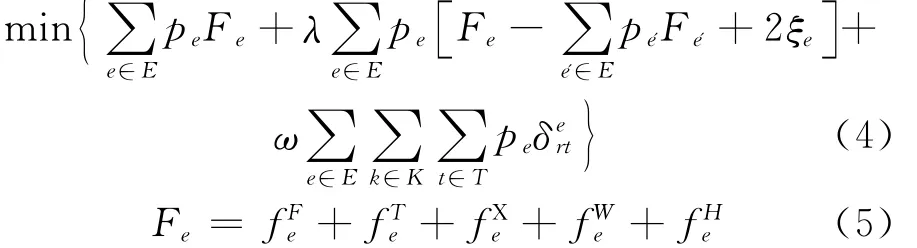
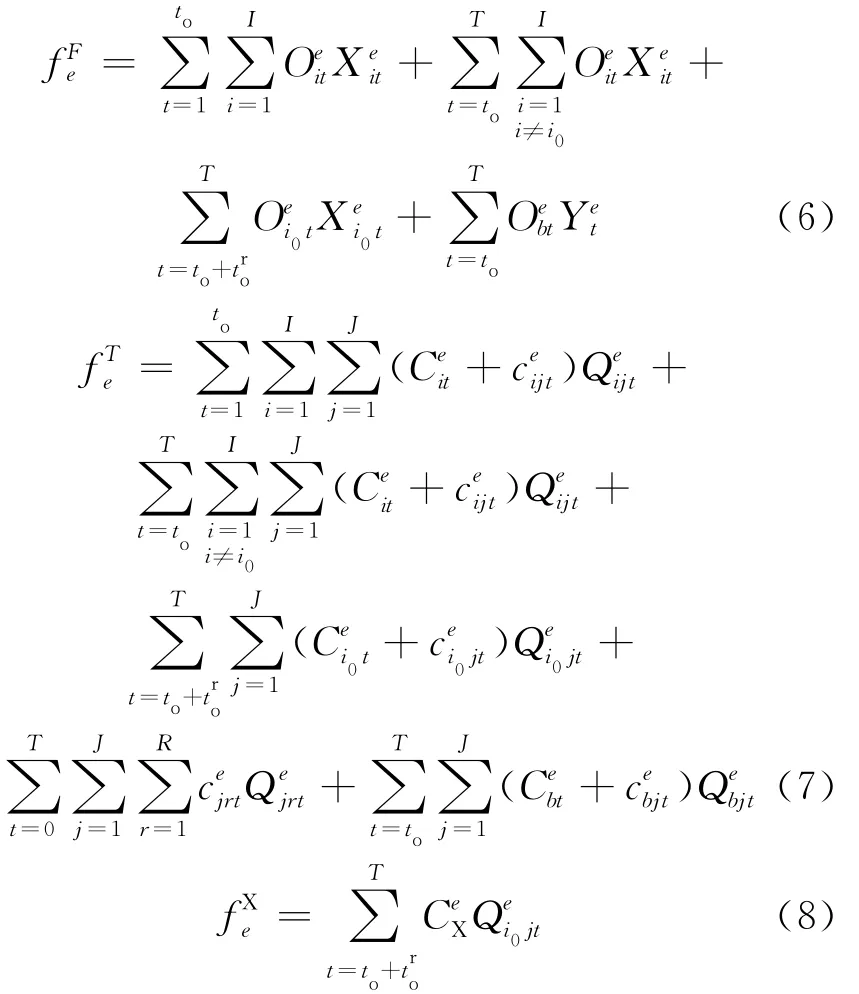
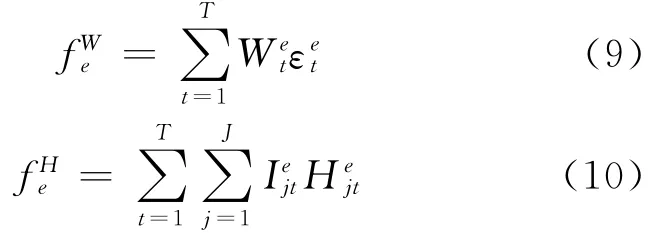
约束条件如下：

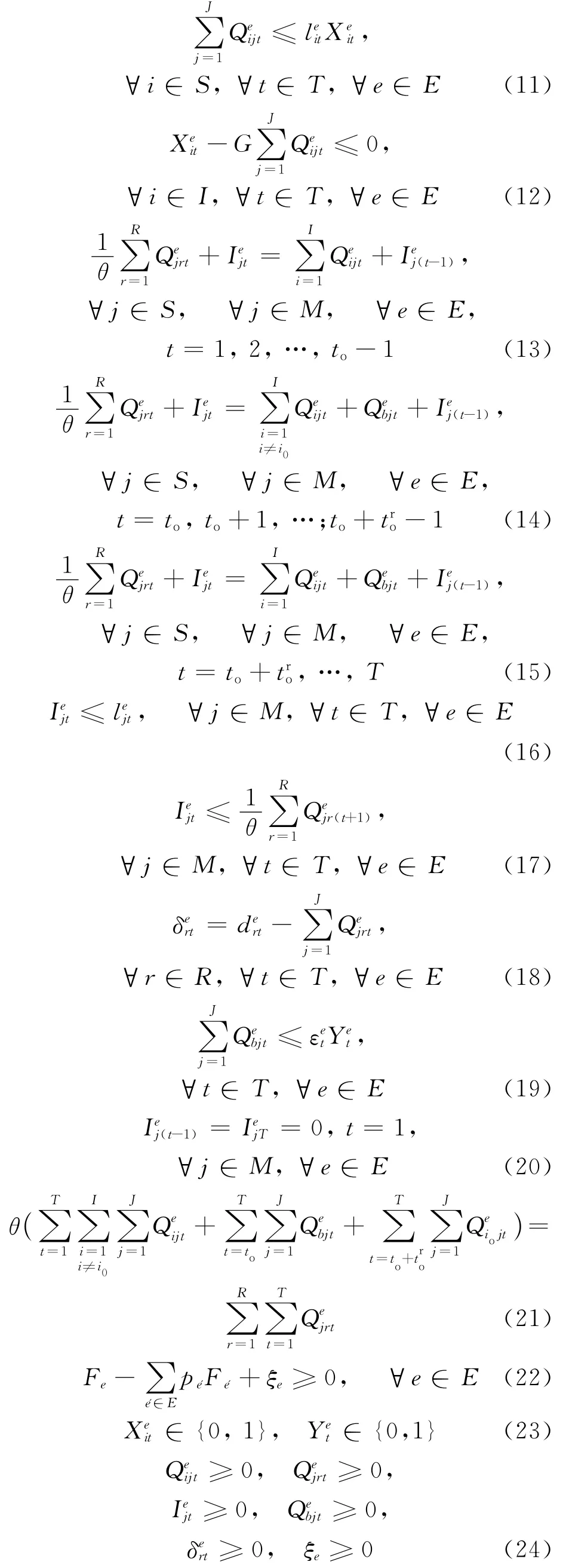
约束条件中，（11）式是主供应商供应能力限制，且仅当主供应商被选择时才允许供货；（12）式表示存在供货量时，供应商开启；（13）～（15）式分别表示主供应商中断发生前、中断发生后未修复好主供应商和主供应商修复完成时制造商处货物流量平衡；（16）式为库存量限制；（17）式表示库存货物的先进先出原则，尽可能防止对时间较为敏感的货物发生变质的情况；（18）式为客户未满足需求约束；（19）式为备选供应商的供货量不能大于制造商购买的期权数量，且仅当备选供应商被选择时才能供货；（20）式表示运营周期内期初和期末制造商的库存为0；（21）式表示供应商供应原材料所能生产的产品量与客户收到的产品量相等；（22）式为鲁棒模型的辅助方程；（23）式、（24）式为决策变量约束。

3 实 验

3.1 实验数据

以某服装供应为背景，考虑一个3级服装供应链网络，网络包括3个主供应商、1个备选供应商、3个制造商和3个客户群，供应商将布匹运送至制造商加工制造，制造商在满足需求的前提下可持有一定的安全库存。服装属于季节性产品，人们对同种衣服的需求热情随季节发生变化，假设服装生产的周期为1a，并按季节划分为4个时段。

基于过去经验，假定在给定时段中客户对衣服的需求量是已知的，另外供应商的能力也随着季节的变化而变化且已知。

本文中对供应的不确定性通过不同的场景进行描述，每种场景的发生满足独立的概率分布。

（1）所有场景下，假设主供应商M2在t2时段发生中断，制造商的单位库存成本为10元，供应商单位修复成本为10元，完成修复所需时长为1个时段，期权购买量为1 500件，期权购买成本为5元，原材料转换系数θ＝1，且参数风险厌恶权重ω＝200，可变性权重λ＝1。

（2）假设有3个场景，场景的需求总量依次递增，每个场景发生概率服从均匀分布，分别为pe＝1／3。表1表示不同场景下，时段t1到时段t4产品的需求量。

（3）所有场景下，4个不同时段主供应商供应成本、能力限制、启动成本和备选供应商启动成本、期权执行成本见表2所列。

库存成本、库存能力和相关运费不一一列出。

表1 3种场景4个时段客户需求量

表2 4个时段主供应商供应成本、能力限制、启动成本，备选供应商启动成本、期权执行成本

3.2 实验结果

基于上述数据，本文使用Matlab R2013a软件通过yalmip线性规划求解器调用Cplex对模型进行求解。在没有中断发生的情况下，鲁棒模型得到的供应商选择见表3所列，此时最优供应链配置下的成本为904 470元，在不考虑应急策略时，当发生中断事件，中断供应商所分配的供应任务将无法完成，造成下游的缺货。假设在t2时段供应商S2发生中断，中断前的库存在中断时段仍能使用，则供应链恢复结果见表4、表5所列，此时供应链总成本为1 032 913元，与正常情况下的成本相比并未有大幅度上升，但降低了中断造成的缺货影响，以较低的成本缓解了风险对供应链造成的冲击。

表3 正常情况下，3种场景4个时段供应商选择

表4 中断情形下，3种场景4个时段供应商选择

表5 中断情形下，3种场景4个时段备选供应商选择

表6和表7分别表示正常和中断情况下，不同制造商处的应急库存量。正常情况下，3个场景总安全库存量为4 200件，而中断情形下的总应急库存量为5 400件，中断发生后库存总量与正常情况下的相比有较大的增加，这是由于应急库存策略对短期中断效果较好，企业在中断风险发生后提高对风险的警惕，安置较多的库存以备不时之需。

由表3～表7可知，面对中断风险时，采取的应急策略组合不同。在场景1中，当中断事件发生时立即启用库存，当库存无法满足中断造成的缺货时，在决策者风险态度一定的前提下，行使期权启动备选供应商，完成t2时段的供货，在长远运营的前提下选择在t3时段进行中断供应商修复策略；在场景2和场景3中，供应链没有立即修复中断供应商，由于考虑了风险和成本等因素，t2时段使用备选供应商进行供货，t3时段正常供应商能力充足能够完成正常运营，因此延迟修复供应商S2是最佳的选择。从3种中断场景中可以看出，最终中断供应商都得到修复，因为就长期而言，随着供货量的积累，内部主供应商具有较大的成本优势。

表8所列为不同制造商的货物流量，根据统计得出，所有场景下制造商M1处的总流量为4 550件，M2处的总流量为22 450件，M3处的总流量为12 600件，根据流量分析得出，制造商M2处在主要制造商地位，其次为制造商M3。当供应链设计中有制造商数量的约束时，根据分析的结果，可优先考虑选择制造商M2，其次选择制造商M3和M1。当网络中制造商较多且制造能力冗余时，该结论具有更高的实用价值。

表7 中断情形下，3种场景4个时段制造商处的库存 件

表8 中断情形下，3种场景4个时段制造商处的流量

3.3 鲁棒性分析

2.2节中目标函数（4）式使用了表示对未满足需求的风险厌恶权重ω，目的是权衡解决方案鲁棒性和模型鲁棒性。供应能力一定的情况下，未满足需求量会受到风险权重ω的影响。当ω为0时，代表该决策者为风险偏好型，说明需求短缺不会对其造成太大的影响；当ω增加，说明决策者对未满足的需求重视程度增加，此时决策者是风险厌恶型，ω越大说明决策者的风险厌恶程度越大。因此变化权重ω可以在成本与需求满足率之间做出权衡，得出不同类型决策者的最佳决策。同样可变性权重λ可能有不同的取值代表决策者对变化幅度的偏好，其对决策结果有着不同的影响。将基准设置为ω＝200，λ＝1，分析不同ω、λ取值对网络设计解决方案鲁棒性（总成本）和模型鲁棒性（未满足需求量）的影响，结果如图2和图3所示。

图2表明随着风险厌恶权重的增加，总成本上升，即解决方案鲁棒性降低；未满足需求量越小，需求满足率上升，即模型鲁棒性增强，这是以总成本的上升为代价的，最终期望的未满足需求为0。决策者可以将成本与未满足需求间的关系进行权衡，通过设置较大的ω可以避免未满足需求的发生。ω＝200时成本较高为1 032 913元，较正常情况下成本增加14.2%，但缺货为0；ω＝140时，成本降低为1 018 843元，较正常情况下成本增加12.6%，场景3发生需求未满足现象，其余的2个场景具有较高的鲁棒性，当ω＝130时，成本降低为1 014 613元，此时场景1和场景3均发生缺货。当供应链中有预算约束时，鲁棒模型具有更好的实用性，根据预算的限制选择合适的ω可以在降低总成本同时保证设计的供应链对较多场景具有鲁棒性。

图3表明随着可变性权重λ的增加，未满足需求量上升，模型鲁棒性下降；同时总成本上升，解决方案的鲁棒性下降。在可变性权重为1.0时模型鲁棒性和解决方案的鲁棒性同时达到最大，总成本为1 023 393元，缺货量为0。在λ为2.0时模型鲁棒性和解决方案的鲁棒性对可变性权重的变化将不敏感，此时增大可变性权重将不会对总成本和缺货量有影响。

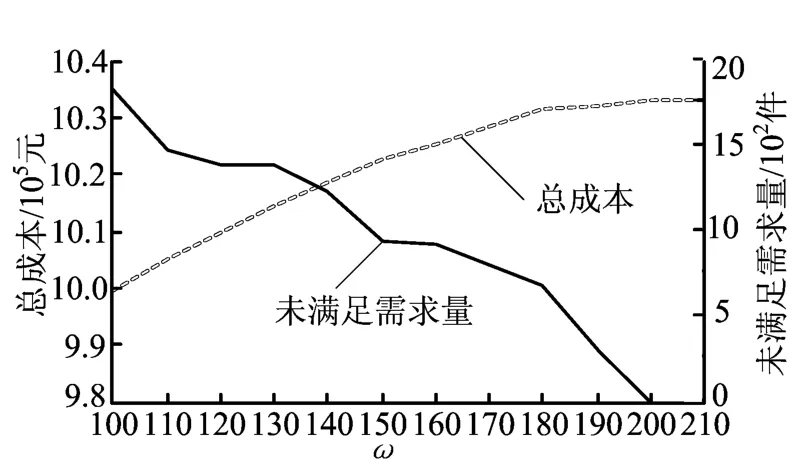
图2 风险厌恶权重ω对鲁棒性的影响

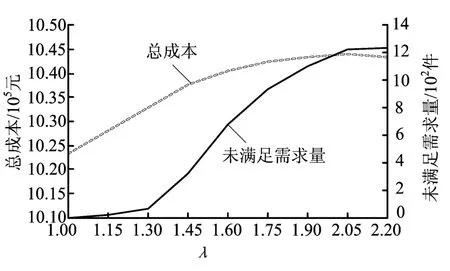
图3 可变性权重λ对鲁棒性的影响

4 结束语

本文建立了鲁棒优化模型，设计了供应和需求不确定下的中断修复供应链，在中断基本模型的基础上引入鲁棒优化概念和应急策略组合，在多场景、多时段下确定了最优的供应商选择和分配决策，并得出中断情形下应急策略的组合。提出的鲁棒模型以成本最小为目标协调供应和需求，并通过风险权重和可变性权重的敏感性分析展示了供应链成本和需求未满足量的权衡：随着风险权重的增加，供应链成本增加，需求未满足量减少，表明模型的鲁棒性是以成本为代价的；随着可变性权重的增加，供应链成本增加，需求未满足量增加，表明可变性权重与风险厌恶权重对供应链有着不同的影响，供应链决策者需根据自身情况设置合理的权重系数，以设计出更符合要求的供应链。根据最优的供应链网络配置，对所有场景下制造商的利用率进行分析，在有预算限制的条件下，为制造商的优先选择提供了依据。

未来的研究方向：在考虑中断供应链网络设计时可考虑碳排放等环境保护约束，建立缓解风险的绿色供应链；可以考虑不同供应商具有不同的中断概率，在权衡风险概率和总成本的基础上进行供应链网络的设计。

［1］ Ruiz－Torres A J，Mahmoodi F.A supplier allocation model considering delivery failure，maintenance and supplier cycle costs［J］.International Journal of Production Economics，2006，103（2）：755－766.

［2］ 马 成，周永务.期权契约下应对突发事件的供应链协调［J］.合肥工业大学学报：自然科学版，2009，32（3）：430－434.

［3］ 孟翠翠.基于制造商视角的供应链中断风险管理研究［D］.北京：中国石油大学，2009.

［4］ Qi Lian，Shen Z J M.The effect of supply disruptions on supply chain design decisions［J］.Transportation Science，2010，44（2）：274－289.

［5］ Chen Qi，Li Xiaopeng.Joint inventory－location problem under the risk of probabilistic facility disruptions［J］.Transportation Research Part B：Methodological，2011，45（7）：991－1003.

［6］ 闫 妍.基于弹性供应链的易腐品物流配送计划［J］.系统管理学报，2012，21（2）：258－263.

［7］ 秦绪伟，喻海飞，黄小原.有限能力物流系统防御设计随机模型及算法［J］.东北大学学报：自然科学版，2012，33（6）：904－908.

［8］ 高 聪，关志民，寇娟娟，等.供应失效风险下可替代原材料供应网络的设计问题［J］.东北大学学报：自然科学版，2013，34（5）：737－739.

［9］ 赵小松，李 莉，吴 优.考虑失效相关性的普通药品供应中断模型［J］.工业工程，2013，16（1）：74－78.

［10］ Nejad A E，Niroomand I，Kuzgunkaya O.Responsive contingency planning in supply risk management by considering congestion effects［J］.Omega，2014，48：19－35.

［11］ Peng Peng，Snyder L V.Reliable logistics networks design with facility disruptions［J］.Transportation Research Part B：Methodological，2011，45（8）：1190－1211.

［12］ Azad N，Davoudpour H.A new model to mitigating random disruption risks of facility and transportation in supply chain network design［J］.International Journal of Advanced Manufacturing Technology，2014，70：1757－1774.

［13］ Ruiz－Torres A J，Mahmoodi F，Zeng A Z.Supplier selection model with contingency planning for supplier failures［J］.Computers ＆ Industrial Engineering，2013，66（2）：374－382.

［14］ Mulvey J M，Ruszczynski A.A new scenario decomposition method for large－scale stochastic optimization［J］.Operations Research，1995，43：477－490.

［15］ Yu C S，Li H L.A robust optimization model for stochastic logistic problems［J］.International Journal of Production Economics，2000，64：385－397.