基于置信规则库系统茶叶市场消费者偏好测度

夏旻旻， 李兴国， 付 磊， 杨 颖

（1.合肥工业大学 管理学院，安徽 合肥 230009；2.安徽农业大学 经济管理学院，安徽 合肥 230036）

茶叶有包装、品牌、价格、品质、保健作用、存放年份等多种感官属性［1－2］。消费者在选购茶叶时只能通过茶叶的感官属性衡量，如何对茶叶的多个属性进行综合评价，获得不同茶叶的综合排序，以及如何进一步测度消费者的偏好，是多属性决策问题，当前的方法主要有层次分析法（AHP）［3］、模糊集［4］、D－S证据理论［5－6］以及证据推理等方法。

文献［7］在D－S理论的基础上进一步改进，将未知部分分配给幂集，不仅没有违背贝叶斯推理的过程，也解决了冲突证据的整合。文献［8－9］结合权重和可靠性，系统地提出证据整合的证据推理（evidential reasoning，ER）规则。这样的规则可以合理地解决不确定多目标决策问题［10］。然而证据推理只能整合相互独立的证据，这在实际应用中受到很大的局限［11］。

在实际决策中，属性间往往存在非线性的因果关系，传统的建模方法很难在系统中反映这样的关系，因此，文献［12］提出基于ER算法的置信规则库（belief rule－based，BRB）系统。此系统在项目组合、临床诊断、产品优化等众多领域有着重要的实际应用［13－16］。文献［17］利用 BRB 系统成功预测柠檬饮料市场的消费者偏好，并设计新产品。

BRB系统的关键是建立规则库，反映属性间的因果关系。文献［13－17］都是由领域内的专家根据专业知识和经验给出。然而，一方面，由于受专家自身的主观性以及专家对专业领域知识了解程度的影响，专家给出的规则具有很大的主观性，不一定完全可靠；另一方面，某些领域可能没有这样的专家。因此，如何建立规则库是一个重要课题。关联规则是从数据库中挖掘项集之间的关联性［18］，是发现规则的有效方法。

本研究基于BRB系统，通过问卷调查，获取相关数据，从数据中挖掘规则，建立BRB系统，构建茶叶的评价模型，测度消费者偏好，计算不同茶叶的综合得分并排序，为产品的设计提供重要的决策信息。

1 置信规则库系统（BRB）

1.1 系统模型

多目标决策问题往往存在多层指标［12］，如图1所示。

图1 指标模型

总体A由k个指标A1，A2，…，Ak决定，第i个指标Ai又由mi个下层指标Ai1，Ai2，…，Aimi决定。对于指标Ai，其属性值有时不宜直接测量，需要通过其下层指标衡量，而下层指标Ai1，Ai2，…，Aimi与Ai存在非线性的因果关系。这样的因果关系可以利用规则表示。

1.2 规则

一般地，知识库R＝〈U，A，D，F〉。其中，U＝｛Ui，i＝1，2，…，T｝为前驱属性集；A＝｛A1，A2，…，AT｝，Ai＝｛Aij，j＝1，2，…，Ji＝｜Ai｜｝为Ui的值域；D＝｛Dn，n＝1，2，…，N｝为结果属性集；F为逻辑函数。定义规则Rk：其中，规则权重为θk；属性权重为σk1，σk2，…，σkTk，k∈｛1，2，…，L｝；βjk表示结果属性为Dj的信度，表示信息完全表示信息不完全。

例如，规则：if精美程度为“精美”∧便携性为“方 便”，then 包 装 为 ｛（一 般，0.04），（喜 欢，0.96）｝。即如果属性精美程度的取值为“精美”且属性便携性的取值为“方便”，则0.04的信度认为包装为“一般”，0.96的信度认为包装为“喜欢”。精美程度和便携性称为前驱属性，包装称为结果属性。

规则权重反映这条规则的重要程度，属性权重反映属性在此规则中的重要程度。对于某一具体的决策问题，规则可以由专业领域的专家根据专业知识和经验给出。本文运用关联规则理论，利用Weka软件挖掘规则，建立规则库。

1.3 关联规则

设I＝｛I1，I2，…，Im｝是项的集合，任务相关的数据D是数据库事务的集合，其中每个事务T是项的集合，使得T⊆I，A是一个项集，事务T包含A当且仅当A⊆T。

关联规则是形如A⇒B的蕴含式，即ifAthenB，其中A称为前件，B称为后件，A⊂I，B⊂I，并且A∩B＝∅。规则A⇒B在事务集D中成立，具有支持度s，其中s是D中事务包含A∪B的百分比，即s（A⇒B）＝P（A∪B）。

规则A⇒B在事务集D中成立，具有置信度c，其中c是D中包含A的事务同时包含B的百分比，即c（A⇒B）＝P（B｜A）。

1.4 规则推理

对于第k个规则，假定其输入为：）。其中，。

规则k的前驱属性的总次数αk可以表示为：αk＝，…，）。其中φ为规则k中Tk个前驱属性的聚集函数，σki（i＝1，2，…，Tk）为属性权重。在规则库系统中［12］，逻辑关系概率积“∧”、概率和 “∨”的聚集函数分别为：

本文规则的逻辑关系均为概率积，因此，选择加权乘法聚集函数计算αk：

从而第k个规则的激活权重为：

其中，θk为规则的权重。

由此，运用ER算法［9］对规则进行推理：

进行聚合，有｛Dj｝：

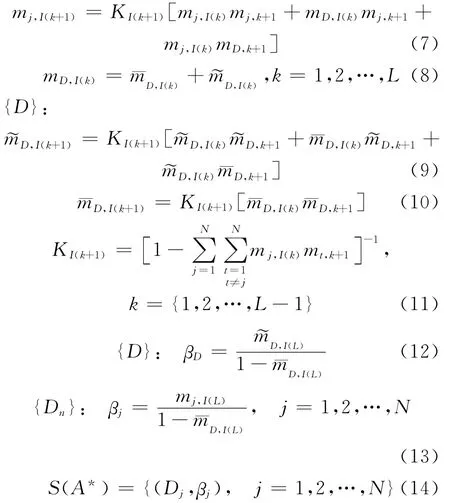
其中，Dj为属性结果的第j个取值；βj为其信度；βD为未知信度。这是一个递归的正交和过程，可以借助IDS软件求解。结合效用函数，计算方案的最终得分为：

2 基于BRB系统的消费者偏好测度

2.1 影响消费者偏好的茶叶属性的确定

消费者在选购时不可能考虑所有的属性，属性的重要程度有高有低。另外，各层属性间存在非线性的因果关系，例如，消费者的偏好与茶叶的价格，不一定是价格越低消费者越喜欢。

为了避免模型过于复杂，通过调查，选取部分重要属性来构建模型。为此，作者走访了多家较大规模的茶叶实体店，访谈［19］茶叶销售人员和普通消费者，通过预调研获取消费者选购茶叶时各属性的重要性，见表1所列（重要程度对应的分值分别为：1极不重要，2很不重要，3不重要，4普通，5重要，6很重要，7极其重要）。

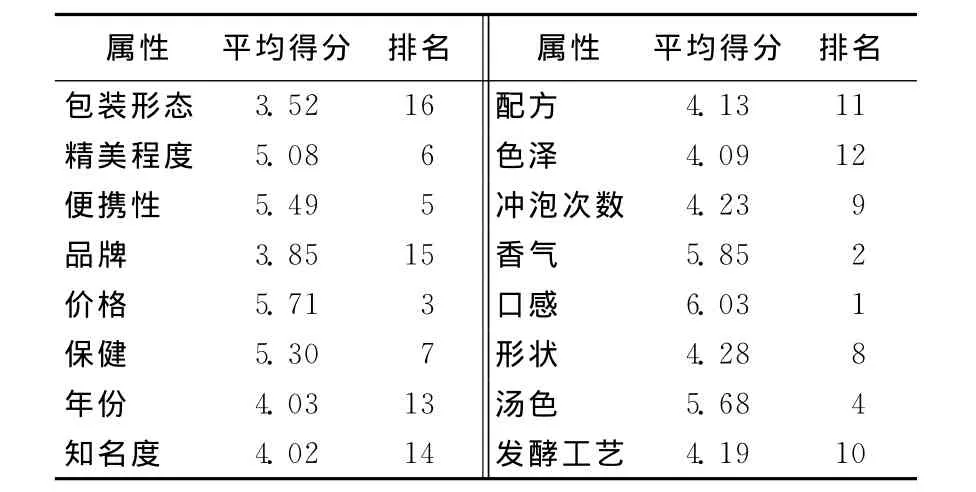
表1 属性重要性得分

2.2 消费者偏好测度的BRB系统

选择平均得分大于5的属性建立模型如图2所示。

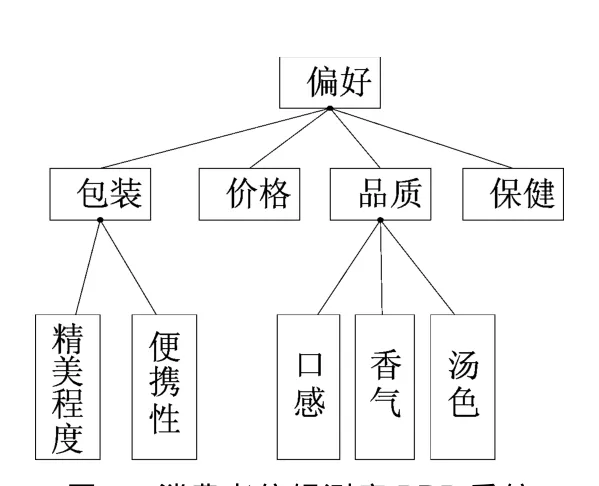
图2 消费者偏好测度BRB系统

此模型包括3个BRB子系统：精美程度和便携性决定包装；口感、香气和汤色决定品质；包装、价格、品质和保健作用决定了消费者对此茶叶的喜好程度。对于某一种茶叶，输入精美程度、便携性、口感、香气、汤色、价格和保健的属性值，可以计算出消费者对此茶叶的偏好。

2.3 茶叶市场消费者偏好测度实例

在这些指标中，上层指标与下层指标存在非线性的因果关系。笔者参照模型并与专业人员讨论以设计问卷。被访问者选择一种比较了解的茶叶，填写此茶叶的各属性值，并给出其对此茶叶的喜好程度。依此从数据中挖掘属性间的非线性因果关系。

本文采用网络调查方法，共收集数据200余份，经过数据处理，去除无效问卷，最终选择192条数据进行试验。下面给出测度实例的计算过程。

（1）挖掘各系统的规则库。从包装属性中截取部分数据，以此为例，见表2所列（表中数字代表问卷中各选项属性的序号。精美：1不精美，2一般，3精美；便携：1不方便，2一般，3方便；包装：1不喜欢，2一般，3喜欢）。

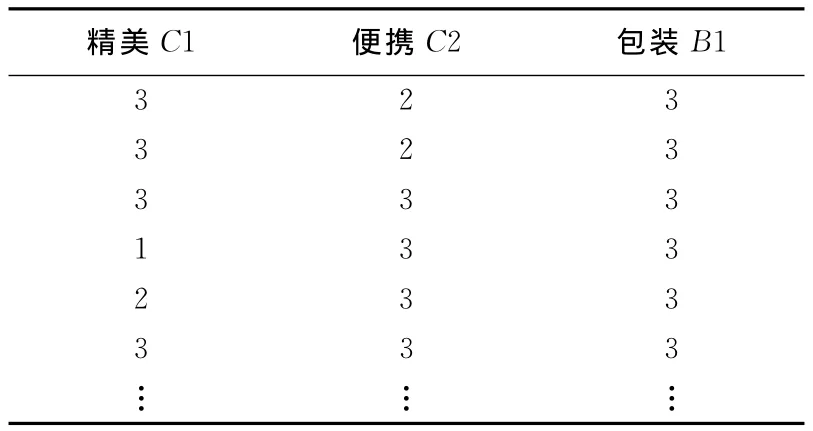
表2 包装数据

将数据导入 Weka中，运算关联规则，结果如下：

Best rules found

1.C1＝1B1＝3 4⇒C2＝3 4conf：（1）

2.C1＝1C2＝2 3⇒B1＝2 3conf：（1）

3.C2＝2B1＝1 3⇒C1＝2 3conf：（1）

4.C1＝3C2＝3 27⇒B1＝3 26conf：（0.96）

5.C2＝3B1＝2 32⇒C1＝2 29conf：（0.91）

6.C2＝2B1＝2 59⇒C1＝2 50conf：（0.85）

……

在运算结果里选取后件为结果属性B1的蕴含式，如结果4：

C1＝3C2＝3 27⇒B1＝3 26conf：（0.96）。

此结果的意义是：数据库中有27个事务包含C1＝3C2＝3，在C1＝3C2＝3的事务中同时B1＝3的有26个，则此蕴含式的支持度s＝27／192＝0.14，置信度c＝0.96。从数据库中统计出包含C1＝3C2＝3余下的事务，同时包含B1＝2的有1个，包含B1＝1的有0个，即存在蕴含式C1＝3C2＝3 27⇒B1＝2 1conf：（0.04）；C1＝3C2＝3 27⇒B1＝1 0conf：（0）（此时，由于conf的值较小，运算结果没有此蕴含式，如果conf大于设置的参数值，则结果中包含此蕴含式，无需统计）。将这些前件相同的蕴含式整合，置信度c作为规则结果的置信度βjk即为规则：

ifC1＝3C2＝3thenB1＝ ｛（1，0），（2，0.04），（3，0.96）｝。

蕴含式的支持度同时也反应规则的重要性，将支持度s赋予规则权重θ＝s。由此可得规则：

if精美程度为“精美”且便携性为“方便”then包装 为 ｛（不 喜 欢，0），（一 般，0.04），（喜 欢，0.96）｝，此规则权重为0.14。

运用该方法依次计算得到关于包装的规则库，见表3所列。

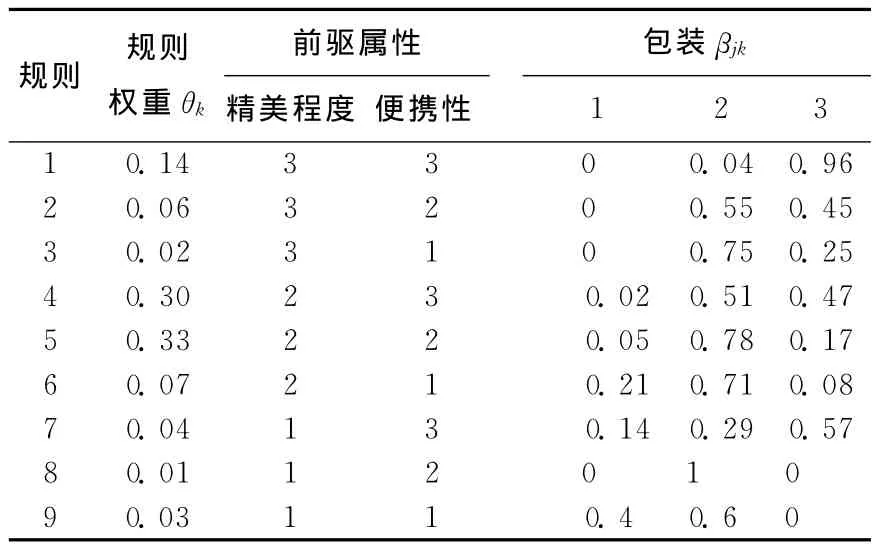
表3 包装子系统规则库

采用同样方法依次建立子系统品质和系统总体偏好的规则库。

（2）输入属性值。对问卷数据进行统计，得到5种常见茶叶的输入值S（A＊i，εi），见表4所列。

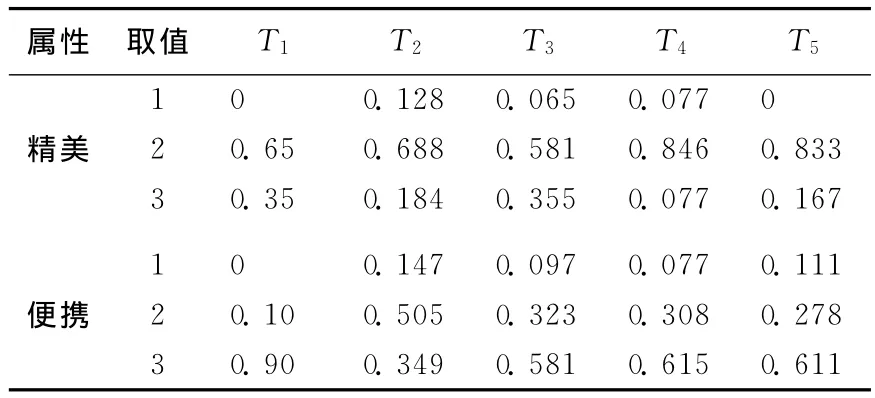
表4 5种茶叶的2种属性值

以茶叶T1为例，对于子系统包装，输入精美程度：（1，0），（2，0.65），（3，0.35）；便携性：（1，0），（2，0.10），（3，0.90）。

（3）计算激活权重wk。由（1）式计算αk（k＝1，2，…，9），再由（2）式计算wk（k＝1，2，…，9）。

（4）整合规则。将βjk和结果wk带入（3）～（14）式对规则进行整合，由于计算量较大，本文利用IDS软件进行计算。运算得T1的包装结果为：（1，0.017 1），（2，0.459 4），（3，0.523 5）。

同理计算品质系统的结果为：

（1，0.258 5），（2，0.588 6），（3，0.128 9）。

将包装、价格、品质和保健作为输入，得到偏好的结果为：

（1，0），（2，0.000 2），（3，0.197 9），

（4，0.738 8），（5，0.063）。

同理计算其他茶叶的偏好。

（5）计算得分。取线性效用函数［12］，u（1）＝0.2，u（2）＝0.4，u（3）＝0.6，u（4）＝0.8，u（5）＝1，代入（15）式计算5种茶叶总得分，结果见表5所列。

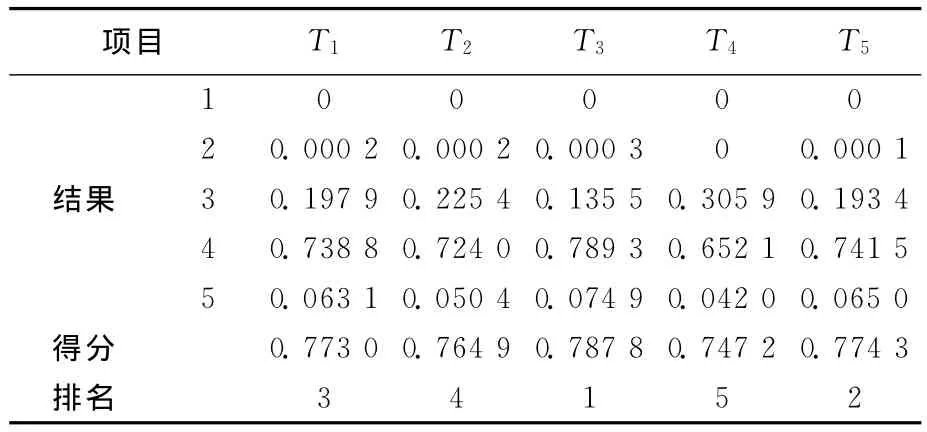
表5 5种茶叶计算得分结果

2.4 结果对比与分析

从收集的数据中统计题项“总体来说，你喜欢此种茶叶吗？1.非常不喜欢，2.不喜欢，3.一般，4.喜欢，5.非常喜欢”。统计这5种茶叶的填写数量，以及选择各个结果的比例，同样结合效用计算得分和排名，见表6所列。

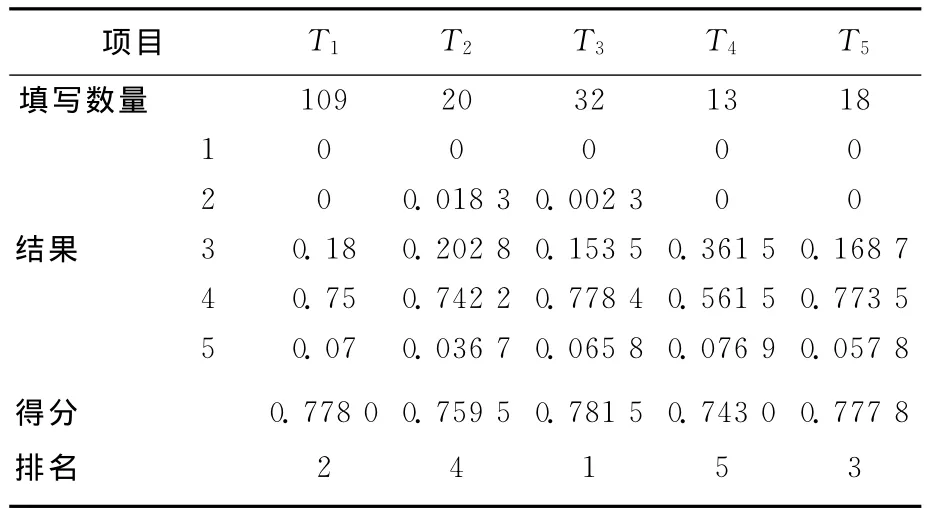
表6 5种茶叶统计得分结果

将表5置信规则库系统计算的结果与表6统计结果对比可以看出，2种方法的得分和排名基本一致，这充分证明本文运用关联规则理论建立规则库的可行性，也进一步说明置信规则库系统的实用性。这样的系统可以合理地对市场的消费者偏好进行测度，从而为复杂产品的测度提供有效的方法。同时在对比中也看出，2种方法对T1和T5的排名不同，这是因为，统计的数据中T5的填写数量较少，导致统计数据不够准确。因此，在今后的应用中，提高收集数据的数量至关重要，是决策分析的前提。

进一步，此系统可用于产品的设计研发决策。对于研发人员，设计多种属性值，输入系统进行计算，比较它们的总得分，从中选择得分最高的属性值设计产品。如果决策者觉得得分不理想，可以不断调试输入的属性值，直到其总得分值是决策者认为最理想的值。

3 结束语

规则可以合理地反映属性间的因果关系，置信规则库系统可以有效地对不同的方案进行评价。置信规则库系统的关键在于规则的建立，通过专家建立的规则，会受到专家个人知识与个人喜好的影响，主观性较强。通过关联规则，在数据中挖掘规则，更加客观、准确。本文通过问卷收集数据，借助软件计算，有效地对茶叶进行评价，并且对新的茶叶产品的设计提供了一定的参考。

置信规则库系统在很多领域都有应用，系统属性的数目与系统的复杂度成正比，而属性数目与方案评价的准确性成反比，因此，寻找复杂度与准确性的平衡，合理选择属性的数目是置信规则库系统的一个重要研究方向。

［1］ 黄继轸.论茶叶品质的构成及品质评定［J］.茶叶通报，2000，22（2）：19－21.

［2］ 叶乃兴.茶叶品质性状的构成与评价［J］.中国茶叶，2010（8）：10－11.

［3］ 许树柏.层次分析法原理［M］.天津：天津大学出版社，1988：1－22.

［4］ Zadeh L A.Fuzzy sets［J］.Information and Control，1965（8）：338－353.

［5］ Dempster A P.A generalization of Bayesian inference［J］.J.R.Stat.soc.，B，1968，30（2）：205－247.

［6］ 张什永.贝叶斯网不确定性推理研究［D］.合肥：中国科学技术大学，2010.

［7］ Yang Jianbo，Singh M G.An evidential reasoning approach for multi－attribute decision making with uncertianty［J］.IEEE Transactions on System，Man and Cybernetics，1994，24（1）：1－18.

［8］ Yang Jianbo，Xu Dongling.Nonlinear information aggregation via evidential reasoning in multi－attribute decision analysis under uncertainty［J］.IEEE Transactions on System，Man and Cybernetics－Part A：Systems and Humans，2002，32（3）：376－393.

［9］ Yang Jianbo，Xu Dongling.Evidential reasoning rule for evidence combination［J］.Artificial Intelligence，2013，205：1－29.

［10］ 李 磊，裴 凤.基于熵权和证据推理的多属性决策方案评价方法［J］.合肥工业大学学报：自然科学版，2010，33（9）：1396－1400.

［11］ 周 谧.基于证据推理的多属性决策中若干问题的研究［D］.合肥：合肥工业大学，2009.

［12］ Yang Jianbo，Liu Jun，Wang Jin，et al.Belief rule－base inference methodology using the evidential reasoning approach－RIMER ［J］.IEEE Transactions on System，Man and Cybernetics－Part A：Systems and Humans，2006，36（2）：266－285.

［13］ Chen Yuwang，Yang Jianbo，Xu Dongling.Belief rulebased system for portfolio optimization with nonlinear cash－flows and constraints［J］.European Journal of Operational Research，2012，223：775－784.

［14］ Kong Guilan，Xu Dongling.A belief rule－based decision support system for clinical risk assessment of cardiac chest pain［J］.European Journal of Operational Research，2012，219：564－573.

［15］ Chen Yuwang，Yang Jianbo.Inference analysis and adaptive training for belief rule based systems［J］.Expert System with Applications，2011，38：12845－12860.

［16］ Li Bin，Wang Hongwei.A belief－rule－based inference method for aggregate production planning under uncertainty ［J］.International Journal of Production Research，2013，51（1）：83－105.

［17］ Yang Jianbo，Wang Yingming.Belief rule－based methodology for mapping consumer preferences and setting product targets［J］.Expert System with Applications，2012，39：4749－4759.

［18］ 沈 斌.关联规则技术研究［M］.杭州：浙江大学出版社，2012：1－51.

［19］ 翟年祥，方昌勤.六安市农村敬老院现状及入住满意度的调查与分析［J］.合肥工业大学学报：社会科学版，2014，28（2）：60－65.