整合发放神经元模型突触输入参数估计

王 锋， 焦贤发

（合肥工业大学 数学学院，安徽 合肥 230009）

在神经模型中，Hodgkin－Huxley模型（H－H模型）能够精确地模拟真实神经元的放电行为［1］，因此H－H模型对于人们研究神经元活动的动力学机制具有重要意义。利用H－H模型神经元来构建神经网络［2］时，尽管能很好地再现神经回路行为，但由于每个神经元模型均要用多个非线性微分方程来描述，神经回路模型就会非常复杂，这给模型的数学处理和数值分析带来很多的不便。在构造回路模型时，有时并不需要考虑神经元的内部机制，只需考虑神经元的输入－输出关系。整合发放神经元模型（integrate－and－fire model，IF模型）是H－H模型的简化形式，该类模型能够比较精确地反映单个神经元电学特性和对外部输入的响应。整合发放神经元模型是建立在假定神经元的输入发生在突触处以及神经元的所有输入均具有可加性的基础之上，它把神经元的活动分成阈下电位的整合和达到阈值时的发放及复位2个阶段。在理论神经模型研究方面，如果能够建立输入－输出之间的关系，就能在给定外部输入情况下对输出作出准确的预测。

为了建立神经元输入－输出关系，确定神经模型的内部参数和输入参数是至关重要的。另外，模型有效性可以通过比较仿真模拟得到的估计值与真实数据来定量检测。从统计学角度来看，定量检测首先是对模型中所涉及的参数进行有效的估计，因此参数估计是分析和验证神经元模型的一个重要方面。

模型中的参数［3］可以分成以下2类：

（1）描述神经元本身电化学特性的参数（如膜时间参数、离子通道电导），这类参数通常与细胞的某些内在特性有关，有具体的生物学解释。因此，该类参数对特定的细胞来说，值是固定不变的，同时可以利用一些电生理实验方法测定。

（2）描述神经元输入信号特性的参数，称之为输入参数。输入参数是可变的，只能通过假定神经元膜电位服从给定的模型进行估计，因此输入参数是模型中最重要的参数。

实验数据从本质上分成细胞内记录和细胞外记录［4－6］。对于细胞内记录数据，文献［7］基于首次放电时间（ISI）分布推导出了带有抑制性反转电位的OU模型（Feller模型）中参数估计方法，并提出了在阈下情况和阈上情况下的输入参数矩估计。首次放电时间分布是经验公式，所以利用ISI数据得到的估计方法必然会带来一定的误差。文献［8］提出了利用首次放电时间的密度和转移概率密度来估计输入参数。该方法计算简便、运算速度快，并且对小数据集十分有效。对于细胞外记录数据，文献［9］对未知输入的OU模型中的输入参数进行了估计，并研究了阈下机制下的参数估计，所以在估计过程中不可避免地存在系统误差。文献［10－13］对阈下机制和阈上机制条件下的3种不同的数学模型中输入参数进行估计。为了减小经验公式和神经元放电特性带来的系统误差，本文尽量避免或减少运用经验公式，并且考虑神经元放电阈值特性。

整合发放神经元模型不仅能简单地描述神经元的电生理特性，同时也能够很好地描述神经元动作电位的发放，并且对计算要求相对较低，因此比其他模型更适合用于数学分析处理和数值模拟。然而，在神经系统中噪声是无处不在的，如热噪声、突触噪声等［3］，因此本文考虑突触输入和噪声共同作用情况下的整合发放神经元模型突触输入参数估计。

1 数学模型

整合发放神经元模型把神经元的活动分成阈下电位的整合和达到阈值时的发放动作电位及膜电位复位2个阶段。模型中假定所有神经元均为高尔基Ⅰ型神经元，即神经元输入只有突触输入。对于第1阶段，可以用微分方程来描述［1］，该微分方程如下：

其中，Vi为第i个神经元在始段处的跨膜电位；τ为膜时间常数；Ii（t）为第i个神经元接受突触前神经元的突触输入总和；R为细胞膜电导；V0为静息电位。

然而，在神经系统中噪声是无处不在的，如热噪声、突触噪声等。因此本文考虑突触输入和噪声共同作用情况下的整合发放神经元模型。令Vt＝Vi－V0，则由（1）式可得：

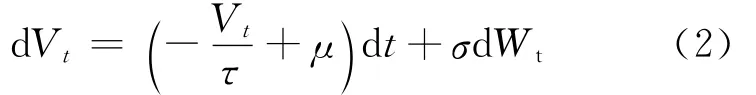
其中，Vt为神经元在t时刻的膜电位；τ为膜时间常数；μ为突触输入总和；σ为噪声强度；Wt为标准维纳过程。

2 突触输入参数估计

2.1 不考虑放电阈值的突触输入参数估计

不考虑阈值行为，神经元的膜电位可以看成是由（2）式所确定的连续变量。对于一个固定时间t，由（2）式确定的Vt为一个高斯随机变量，其均值和方差［11，14］为：

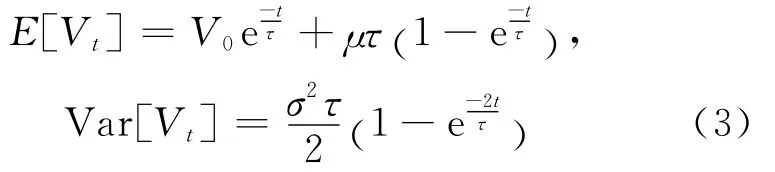
本文所给出的所有估计方法都是利用细胞内记录数据（离散的膜电位数据）进行估计的，是在离散的时间ti＝ih时刻记录的膜电位。由于膜电位是一个连续变量，将离散化的膜电位数据与其均值和方差分别做差，并求出最小平方差，即最小二乘法。构造的最小函数为：

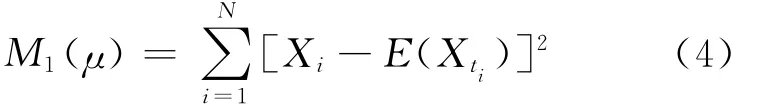
对（4）式关于μ求导，为了使（4）式有最小值，则有：

通过数学推导，可得μ的估计为：

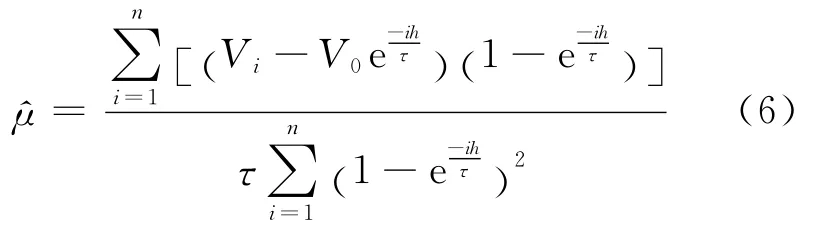
同理，为了得到σ2的估计，用（6）式的代替（4）式中的μ，构造另一个最小函数，即

对（7）式关于σ2求导，并令其值等于0，可得σ2的估计为：

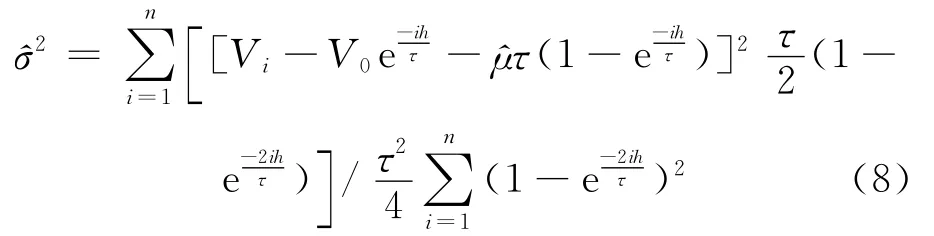
采用四阶－五阶龙格库塔算法模拟膜电位演化过程时取S＝20mV。当μτ＝S时，称为阈值；当μτ＞S时称为阈上；当μτ＜S时称为阈下。3种参数不同取值情况下的膜电位的轨迹如图1所示。

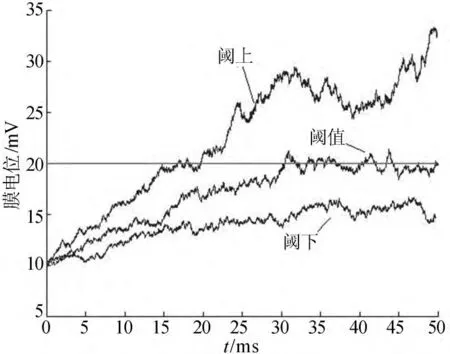
图1 不同刺激模式下膜电位演化图

为了避免偶然性，取3组不同的参数值。噪声强度σ取0.3mV／ms时，突触输入μ为0.8、1.0、1.4mV／ms，膜时间常数τ取20ms，初始膜电位V0取10mV，时间步长h取0.01ms。对每组参数值重复模拟100次得到100组观测值，利用上述理论推导和Matlab软件可以获得100对），所得估计结果见表1所列。

由表1可以看出，当μ为0.8mV／ms时，突触输入的均值为0.806 8，均方误差为0.041 2，表明在突触输入μτ＜S时，阈值情况下突触输入的估计效果好；当μ为1.4mV／ms时，突触输入μ的均值为1.485 8，均方误差为0.382 9，均方误差较大，估计效果不佳。

表1 不考虑放电阈值的数值模拟结果

因此，当突触输入μτ＞S时，阈上情况下突触输入的估计效果不是十分理想。所以最小二乘估计在阈下情况的估计效果要优于阈上情况的估计效果。这主要是由于在估计过程中没有考虑神经元放电阈值行为。事实上，神经元可看作是存在放电阈值特性的可激发系统。当外部刺激强度在阈值以下时称为阈下，神经元轴突膜上只产生被动的去极化电位，而不产生动作电位［13－14］，膜电位会很快衰减到静息电位。而当刺激强度高于阈值时称为阈上，神经元将会发放一个动作电位并通过轴突传导，从而完成从接受信息、处理信息到传递信息的过程［15－16］。所以，最小二乘估计依赖于机制，它仅仅适合阈下情况参数估计，而对阈上情况估计效果不佳。

2.2 考虑放电阈值的突触输入参数估计

如果膜电位的转移概率密度已知并且容易处理，则可以通过极大似然法去估计输入参数。这样参数估计问题就转化为求阈上机制下膜电位的转移概率密度。为了求解出阈上机制下的转移概率密度，首先需要求出阈下机制下的膜电位概率密度［17］。

对应于方程（2）的 Fokker－Planck方程［18－19］如下：

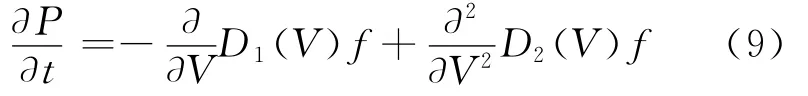
其中，f（V，t｜V′，t′）为膜电位由V′变到V时的概率，称为转移概率密度；D1（V）＝－V／τ；D2（V）＝σ2／2。

为得到微分方程（2）的解析解或数值解，考虑如下初值条件：

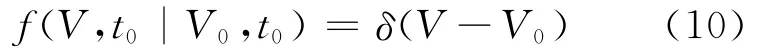
通过数学推导可得到阈下机制下的膜电位转移概率密度为：

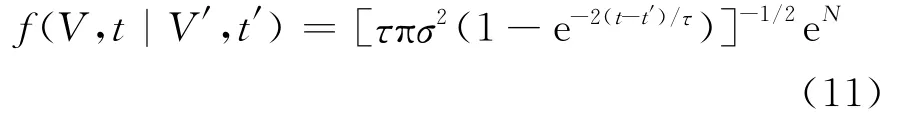
其中，N＝ － ［（V－V0e－（t－t′）／τ－μτ＋ （μτ－V′）e－（t－t′）／τ）2］／［σ2τ（1－e－2（t－t′）／τ）］。

为了得到阈上机制下的膜电位转移概率密度，假定放电阈值为常数Vth，将阈值条件看成是吸收边界。考虑带有吸收边界条件下的Fokker－Planck方程为：

构造似然函数如下：其中，f（Vi，h｜Vi－1）为转移概率密度函数；离散膜电位Vi为在离散时间点ih处的膜电位值；h＝t－t′。

将方程（11）式和（12）式代入方程（13）式得：

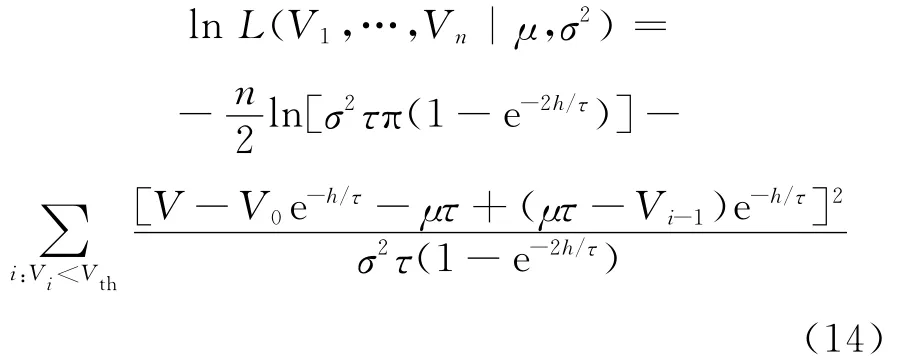
通过数学推导，可得μ和σ2的估计为：

为了研究不同机制下的估计效果，噪声强度σ取0.3mV／ms，突触输入μ分别取0.8、1.0、1.4mV／ms，膜时间常数τ取20ms，初始膜电位V0取10mV，时间步长h取0.01ms，阈值Vth取20mV。对每组参数值重复模拟100次得到100组观测值，利用上述理论推导和Matlab软件可以获得100对），所得估计结果见表2所列。

表2 考虑阈值的数值模拟结果

由表2可以看出，当μ＝0.8mV／ms时，其均值和均方误差分别为0.790 2和0.040 1；当μ＝1.4mV／ms时，其均值和均方误差分别为1.398 0和0.016 6。由此可以看出极大似然估计的效果非常好。因此极大似然估计使用范围更广，而最小二乘估计只使用于阈下活动。为了更好地比较本文给出的最小二乘估计和极大似然估计的优劣，依据膜电位演化方程真实值和估计值得到膜电位演化图如图2所示。

图2 膜电位随时间演化图

从图2a可看出，极大似然估计拟合曲线与真实曲线的匹配程度要高于最小二乘估计拟合曲线与真实曲线的匹配程度，由此可以看出，极大似然估计要优于最小二乘估计。由图2b可看出，极大似然估计拟合曲线与真实曲线相近，基本上将极大似然估计拟合曲线平移一小段距离就可与真实曲线重合。这是因为在估计过程中忽视了不应期的存在。事实上，神经元发放一个动作电位后将进入一个短暂的绝对不应期，在不应期内无论刺激多么大，神经元都不再放电。

3 结束语

本文综合考虑突出输入和噪声共同作用下的整合发放神经元模型，该研究工作是基于模型中内在参数已知，尤其是膜时间常数，并且输入参数是由给定的微分方程（2）所确定。数值分析结果表明，对于2个输入参数μ和σ均可以通过本文所给出的最小二乘估计和极大似然估计进行精确地估计。由本文分析可知，在阈下机制下对于输入参数μ的估计效果，极大似然估计要优于最小二乘估计；而对于输入参数σ的估计效果，极大似然估计要远远优于最小二乘估计。在其他机制下，对于2个参数的估计，极大似然估计都要远远优于最小二乘估计。

本文针对突触输入和噪声共同作用下的整合发放神经元模型，在不考虑放电阈值前提下，采用最小二乘法估计突触输入参数；当考虑神经元放电阈值特性，将放电阈值看成一个吸收边界，导出膜电位转移概率密度函数，然后利用极大似然法估计突触输入参数。最小二乘估计依赖于机制，它仅适合阈下的参数估计，而对阈上无效。极大似然估计适用于所有情况。无论是从适用范围还是估计精度来说，极大似然估计都要优于最小二乘估计。

［1］ 顾凡及，梁培基.神经信息处理［M］.北京：北京工业大学出版社，2009：129－138.

［2］ 丁亚明，王树忠，张志红，等.基于改进神经网络的模糊聚类算法 ［J］.合 肥 工 业 大 学 学 报：自 然 科 学 版，2007，30（8）：934－938.

［3］ Lansky P，Sanda P，He J.The parameters of the stochastic leaky integrate－and－fire neuronal model［J］.J Comput Neurosci，2006，21：211－223.

［4］ Paninski L，Pillow J，Simoncelli E.Comparing integrate－andfire－like models given intracellular and extracellular data［J］.Neurocomputing，2005，65：379－385.

［5］ H¨opfner R.On a set of data for the membrane potential in a neuron［J］.Math Biosci，2007，207：275－301.

［6］ Mullowney P，Iyengar S.Parameter estimation for a leaky integrate－and－fire neuronal model from ISI data［J］.J Comput Neurosci，2008，24：179－194.

［7］ Ditlevsen S，Lansky P.Estimation of the input parameters in the Feller neuronal model［J］.Phys Rev E，2006，

73：061910.

［8］ Ditlevsen S，Lansky P.Parameters of stochastic processes estimated from observation of first－hitting times：application to the leaky integrate－fire neuronal model［J］.Phys Rev E，2007，76：041906.

［9］ Ditlevsen S，Ditlevsen O.Parameter estimation from observations of first－passage times of the Ornstein－Uhlenbeck process and the Feller process［J］.Probabilistic Engineering Mechanics，2008，23：170－179.

［10］ Ditlevsen S，Lansky P.Estimation of the input parameters in the Ornstein－Uhlenbeck neuronal model［J］.Phys Rev E，2005，71：011907.

［11］ Lansky P，Ditlevsen S.A review of the methods for signal estimation in stochastic diffusion leaky integrate－and－fire neuronal models［J］.Biol Cybern，2008，99：253－262.

［12］ Bibbona E，Sacerdote L.Errors in estimation of the input signal for integrate－and－fire neuronal models［J］.Phys Rev E，2008，78：011918.

［13］ Joseph H，Guckenheimer J.Parameter estimation for bursting neural models［J］.J Comput Neurosci，2008，24：358－373.

［14］ Bibbona E，Lansky P，Sirovich P.Estimating input parameters from intracellular recordings in the feller neuronal model［J］.Phys Rev E，2010，81：031916.

［15］ Pawlas Z，Lansky P.Distribution of interspike intervals estimated from multiple spike trains observed in a short time window［J］.Phys Rev E，2011，83：011910.

［16］ Ditlevsen S，Lansky P.Only through perturbation can relaxation times be estimated［J］.Phys Rev E，2012，86：050102.

［17］ Kleinhans D.Estimation of drift and diffusion functions from time series data：a maximum likelihood framework［J］.Phys Rev E，2012，85：026705.

［18］ Haken H.The fokker－planck equation［M］.Berlin：Springer－Verlag，1989：100－105.

［19］ 朱位秋.非线性随机动力学与控制［M］.北京：科学出版

社，2003：56－65.