基于数字地图预处理的飞行器航迹规划
2015-03-11王开拓吴学礼
甄 然,王开拓,吴学礼
(河北科技大学电气工程学院,河北石家庄 050018)
随着航空工业的日益发展,通用航空业的效益也在日益提升[1]。相对于民航和军用航空,通用航空的飞行高度一般限制在1 000 m以下,即低空飞行[2]。目前,中国低空空域正在逐步开放,空域中飞行器密度将逐渐增大,由于低空环境复杂,监视飞行器的雷达电波信号会受到地形障碍的阻挡[2],造成信号缺失,不利于飞行器的安全飞行。而增设雷达基站的费用过高,将阻碍通用航空的发展。为了实现低空空域复杂环境下的飞行安全,低空突防技术就应运而生[3]。
低空突防是提高飞行器低空飞行的生存能力、降低突然大打击率的有效措施[3]。早期的低空突防技术只是利用飞行器的纵向机动能力[4],沿着地形起伏飞行的一种简单的地形跟随技术,随着全球卫星定位GPS的广泛使用和数字地图技术的发展[5],低空突防的研究重点转向了包括地形跟随(TA/TF2)、地形回避、威胁和障碍的回避等综合技术上来[4]。低空航路规划的方法有很多,如动态规划法[6]、粒子群法、组合搜索法、参数优化法、A* 搜索法、人工智能法及神经网络法等[7]。文献[7]中Deneton等用动态规划法计算三维最优航迹,由于该方法所需的存储量和计算量随状态空间的维数增加而急剧增加,文中把三维航迹分解为水平方向和垂直方向[7],虽然在一定程度上解决了动态航路规划的计算量问题,但是计算量和存储量依然很大,规划时间也较长。
本文采用文献[8]的方法提取DED数字地图的信息,将静态威胁物与地图地形信息融合,对飞机计划要飞过的地图路线进行数字地图预处理,得到满足各种飞行器不同性能指标的数字地图安全曲面[9]。在飞行器执行任务前用粒子群算法在预处理的地图上进行离线航迹规划,在实际飞行过程中用粒子群算法对突发威胁进行避让,在线修正离线生成的轨迹,从而提高实时航迹规划速度。
1 数字地图处理
数字地图是将实际中的地图信息用一种可实现的编码形式来表示地图数据,目的是用来构建虚拟的客观环境[9],为各种飞行规划提供较为实际的仿真模拟条件。大范围、高精度并且包含有地貌特征丰富的地形高程数据,有助于仿真验证和算法的研究[10]。
1.1 静态威胁信息的转化
随着城市化的快速推进,在低空域飞行过程中飞行器会遇到大量的静态威胁[9],静态威胁又可分为2类:孤立地物和群落地物。孤立地物包括:孤立高耸的建筑、笔直的旗杆、突兀的山峰等等;群落地物包括:城市建筑群、大片的森林等。本文采取文献[7]中提出的把威胁等效为地形的方法,将静态威胁看作等大规模的地形威胁[10],叠加到原始的数字地图上,从而得到融合有地形威胁的综合数字地形图[11]。叠加式如式(1)所示。

式中:zb(i,j)表示融合威胁信息之后的数据;zd(i,j)表示原始地形数据;h是已知或可测的静态威胁高程信息。
由于威胁物是三维立体的,不同的高度对飞行器的威胁程度有所不同[12],针对飞行器在某一高度运行,将三维威胁信息在飞行器运行的高度层做剖面,就可以将三维威胁信息转化为二维平面威胁[12]。威胁维数的降低可以从一定程度上缩短航路规划时间[13],对于成片出现的威胁,用最小的圆或圆弧将威胁包含在内,如图1所示,作以(Wi,Ei)为圆心,以Ri为半径的威胁圆,威胁物由多个缩减到一个,即可缩短飞行器的航迹规划时间[14]。
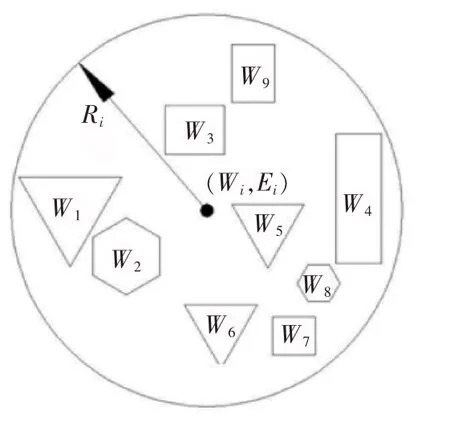
图1 威胁圆构建图Fig.1 Figure of threat round building
1.2 地形回避
地形回避是指飞行器执行任务过程中,通过调整飞行器转向角躲避在同一平面内的威胁目标[15],达到安全飞行的目的。图2所示为飞行器在某一高度层通过转弯躲避对其构成威胁的2座山峰。对飞行器转弯控制点进行计算分析,假设对图2中第1座孤立山峰在飞行器所在的高度平面内作剖面[16],再作山峰剖面的最小内接圆,圆心是(Wi,Ei),半径是Ri。飞行器沿着AB方向接近威胁圆,以一定的坡度角转向时,其运动轨迹是一个圆弧,如图3所示。飞行器的转弯半径R见式(2)。

图2 地形回避图Fig.2 Figure of terrain avoidance

式中:TAS是真空速;g是重力加速度;β是转弯时的坡度角。
假设飞行器是以恒定的坡度角、恒定的速度转弯,其轨迹是一个与历史轨迹相切的圆或是一段圆弧,圆心垂直于向量AB,圆心点坐标可由式(3)求出。

图3 地形回避示意图Fig.3 Figure of terrain avoidance

通过判断转弯圆心与威胁圆圆心的距离即可判断威胁圆是否会对飞行器构成威胁,以及转弯方向是否受限制。
飞行器在平面内自由飞行时,可以向左、向右2个方向转弯,因此会有2个转弯圆心。假设飞行器的速度、转弯时坡度角固定,那么转弯半径就是固定的,不同的是遇到威胁转弯的时机,下面对转弯时机进行分情况讨论:假设一,2个转弯圆心点都满足式(4),那么飞行器还没有触及威胁可以继续飞行;假设二,如果2个转弯的圆心点满足式(5),那么及时向任意一侧转弯都可以避开威胁;假设三,如果一个圆心点满足式(5),另外一个满足式(4),以满足式(5)的圆心点为圆心转向,则轨迹与威胁圆相切擦过;假设四,如果一个满足式(4),另一个满足式(6),则转弯圆心点必须选取在满足式(4)的转弯圆心点到式(5)之前的区间内,如果在式(5)还未转向,则会受到威胁。
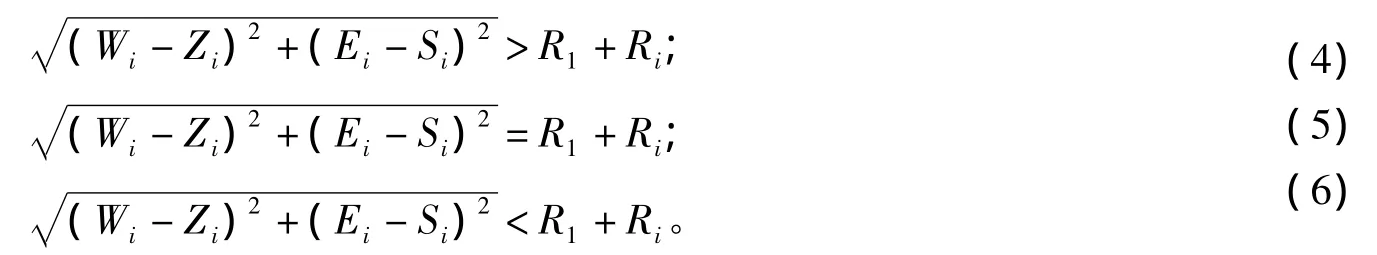
1.3 地形跟随
地形跟随是飞行器根据地势的起伏来改变飞行器的俯仰角[17],跟随地面飞行的一种飞行模式,如图4所示。受到飞行器机动特性限制,俯仰角不能随意选取,因而根据不同飞行器的纵向机动性能对地形进行处理是十分必要的。

图4 地形跟随图Fig.4 Figure of terrain following
数字离散地图的处理方法有很多,例如:滤波平滑技术、迭代法限制地形坡度的平滑算法等等,用滤波平滑算法对地形进行平滑时,不仅会抬高谷底还会削平谷峰[6],迭代法限制地形坡度的平滑算法虽然解决了飞行器最大俯仰角及其最小离地安全间隙的限制问题,但它没有考虑飞行器的最大法向加速度限制[16],本文采用坡度限制和飞行器最大法向加速度的插值算法对数字地图进行修补,用埃尔米特插值算法进行平滑性处理。
插值是处理数字离散地图的基本手段[17],本文采用埃尔米特插值,在使用埃尔米特插值之前,要判断飞行器所要经过的地形坡度角[7],如果地形的坡度角大于飞行器所能承受的最大俯仰角,就要对地形进行修整。图5地形坡度示意图,是xyz三维地图向xoz平面投影的一部分。假设(x1,z1)点是飞行器进入地图的一个节点,通过式(7)来判断与下一个节点的坡度角,如果θi大于飞行器的最大俯仰角θb,那么就对这个点进行增高填补,填补的多少根据式(8)来确定,如果填补后对前一个节点造成影响,使得前一点的坡度角大于飞行器的最大俯仰角,那么就依据式(8)对更前一节点进行填补,以此类推。最后依据式(9)整理航线高程地图,完成满足飞行器机动性能的高程地图处理。

图5 地形坡度图Fig.5 Figure of terrain slope

式中:θi是数字地图地形的俯仰角;θb是飞行器所能承受的最大俯仰角;hi是需要填补的地形高程;zi是原有的地形高程信息;z'i是叠加后的地形高程数据值。
埃尔米特(Hermite)插值是满足节点处等于给定的值,而且节点处导数值也等于给定的导数值的一种插值方法,埃尔米特插值多项式见式(10)。在本文中节点处的函数值就是融合地形威胁并且叠加地形高程数据的离散地图数据值,节点的导数值由式(11)计算得出。

1.4 离地安全高度
飞行器作地形跟随飞行,目的是为了能够更准确地收集地面信息[14]。地面的监视效果与离地高度有极大关系,离地越近效果越好,但离地太近,飞行器撞地的概率将大大增加[3]。为了减少飞行器与地面的碰撞几率,需要距地表有一定的安全高度[4]。国外有关文献认为,低空突防的最佳离地高度为海面上空15~30 m,陆地平原地区上空为60~80 m,丘陵山区上空为120 m左右[14]。
2 低空航迹规划
2.1 指标函数
航迹规划的目的是在满足飞机机械特性和执行具体飞行任务约束的前提下,能够有效躲避影响飞行的险要地形等不利因素,得到一条最优轨迹[18]。最优轨迹的获取首先需要定义代价函数,如式(12)所示。

从式中可以看出,代价函数对于飞行器偏离预定轨迹的距离L、距离威胁距离W以及偏离海平面的垂直距离H进行代价计算,其中k1,k2,k3为相应的惩罚权值,并且有k1+k2+k3=1。
由于飞行器在安全高度曲面上的生存概率较大,高度威胁可以忽略,因而目标函数可简化为式(13)。

式中k1+k2=1,将其写成离散形式,就得到规划航迹点的指标函数。

式中:Li是每个节点偏离预定轨迹的距离;Wi是每个节点距离威胁的距离。
2.2 粒子群算法分析
粒子群算法是一种进化计算技术,1995年由Eberhart博士和kennedy博士提出,源于对鸟群或蚁群捕食的行为研究[13]。种群中每个个体被看作是n维搜索空间中的一个粒子,并在搜索空间中以一定的速度飞行,粒子的飞行速度基于个体的飞行经验和群体的飞行经验进行调整。因而,每个粒子除了对应于一个位置向量 Xi=[xi1,xi2,…,xin],还伴随着一个速度向量 Vi=[vi1,vi2,…,vin],根据跟踪个体最优粒子 Pi=[pi1,pi2,…,pin]和全局最优粒子 Pg=[pg1,pg2,…,pgn]来控制粒子的运动[11]。粒子的速度和位置更新模型见式(15)。
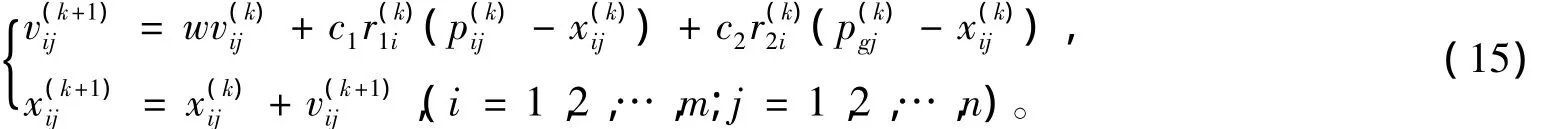
式中:w是惯性因子;c1和c2分别是个体认知系数与社会认知系数[19];r1和r2是[0,1]之间服从均匀分布的随机数;k是迭代数;m是种群的大小;n是空间维数;Pi是个体极值;Pg是全局极值。
惯性因子w用来控制粒子的搜索范围[15],w值越大,全局搜索能力越强,局部寻优的能力越弱,文献[19]讨论了惯性因子的取值问题,采用了线性递减权值策略,如式(16)所示。

式中:N是最大进化代数;k是迭代的代数;wmin和wmax分别是最小和最大权值因子;文献[19]中论述递减策略为wmin=0.4,wmax=0.9。
认知系数c1和c2代表每个粒子朝向个体极值和全局极值的加速权重[19],如果加速度权值较高会使粒子穿越目标区域,过低会降低粒子的搜索能力,找到最优解的时间变长[20]。
当c1=0,c2≠0,如式(17)所示粒子没有了认知能力,只有社会模型,粒子有扩展搜索空间的能力,有较快的搜索速度,由于缺少局部搜索,容易陷入局部最优。

当c1≠0,c2=0,如式(18)所示粒子只有认知能力,粒子之间没有了信息交流,搜索速度变慢[20],不易得到最优解。文献[21]研究了加速因子对粒子群算法收敛速度的影响,其研究结果表明当c1和c2在[0,4]之间取值的时候能够得到较好的解。

pi是个体极值,是每次迭代粒子自身所找到的最优解;Pg是全局极值,是整个种群找到的最优解。最优解是根据式(14)求解每个粒子的代价函数得到的极小值,个体极值根据式(19)进行更新,全局极值根据式(20)进行更新。

2.3 更新位置点的选择
在使用蚁群算法解决航路规划问题时,搜索路径上的蚂蚁总是从航路上的一个安全平面移向另一个安全平面[16],这样能够缩减搜索时间。受到飞行器的速度、俯仰角和翻滚角的限制,就把下一航路点约束在了一个空间曲面A上,如图6所示。
图中点o是蚁群中的一个蚂蚁所处的位置,沿着x轴正方向搜索,θb是飞行器的最大俯仰角,β是飞行器的最大翻滚角,由粗线围成的曲面A是下一时刻的坐标区域,下一坐标点就在曲面A上选取。
2.4 算法步骤
Step1:选择合适的种群大小、粒子维数及最大迭代次数等参数;
Step2:读入信息、威胁信息以及飞行器飞行的起点和终点;
Step3:将已知的地物威胁、地物信息融合到地图地形信息中,得到综合地图地形信息;
Step4:根据飞行器的机动性能对综合地图进行填补和平滑处理,得到平滑的地形地图;

图6 搜索目标点Fig.6 Search the next target
Step5:随机初始化种群,得到初始种群信息;
Step6:根据式(15)对种群进行迭代计算,用式(14)计算每个粒子的代价函数;
Step7:根据式(19)更新个体极值,式(20)更新全局极值;
Step8:根据式(16)更新惯性因子;
Step9:重复Step6—Step8直到到达终点;
Step10:重复Step5—Step9直到最大迭代次数,得到若干条航迹;
Step11:选取航迹代价最小的一条轨迹即最优轨迹;
Step12:输出并显示,完成离线航迹规划。
3 仿真分析
利用文献[8]重建的地形高程数据,将一部分高程数据导入Matlab,生成由340×300个网格组成的三维地形图。假设飞行任务起点B(x0,y0,z0)=(0 km,0 km,0.45 km)、终点S(xg,yg,zg)=(300 km,200 km,0.45 km)、飞行器真空速 T AS=50 m/s、最大坡度角 θ =45°、最大俯仰角θb=±35°、离地最小安全高度h=120 m、代价函数k1=k2=0.5。假设在点(220 km,80 km)处,存在一个圆锥形静态威胁,圆锥底面圆半径为20 km、高为400m。设粒子群的种群规模m=50、迭代次数k=20、个体认知系数c1=2、社会认知系数c2=2、r1和r2取[0,1]之间服从均匀分布的随机数、wmin=0.4,wmax=0.9。假定飞行器燃油充足,机身质量不随飞行时间变化并且没有突发性威胁的理想情况下,对飞行器在执行任务前进行离线轨迹规划实验仿真,实验结果如图7-图12所示。
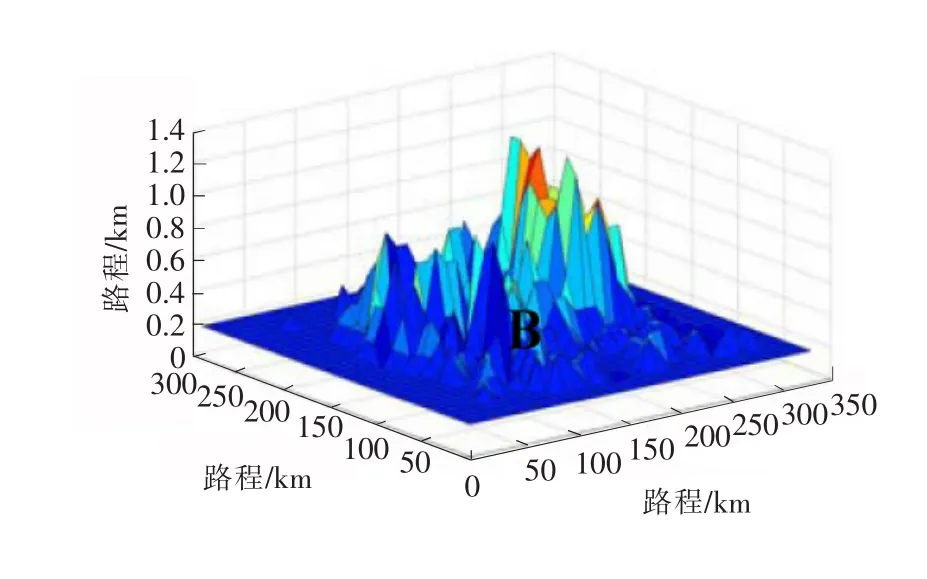
图7 原始地形数据图Fig.7 Original terrain data graph

图8 叠加威胁地图高程数据图Fig.8 Overlaymap figure of threats and elevation data

图9 平滑综合地图Fig.9 Smooth comprehensivemap
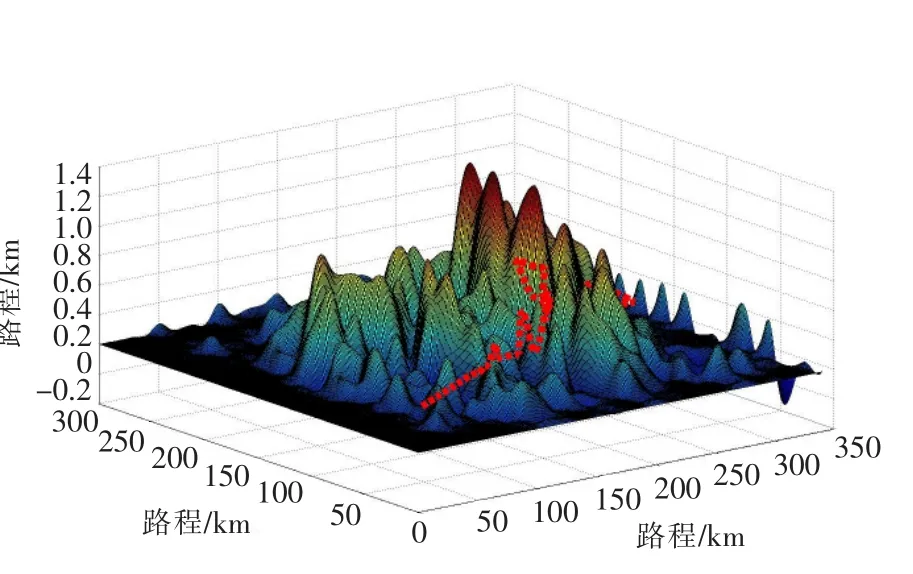
图10 三维航迹轨迹规划图Fig.10 Three-dimensional track prediction
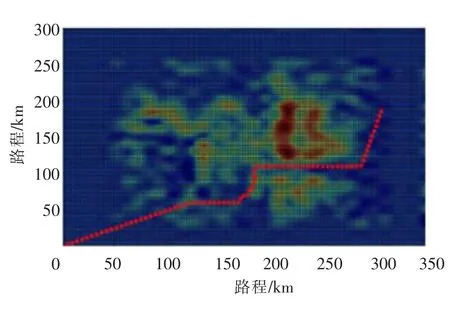
图11 航路规划俯视图Fig.11 Route planning vertical view

图12 航路规划侧视图Fig.12 Rout planning side view
图7是根据DED提取数据文件的原始地形图。由给定的假设可知,在B区域范围内有一个已知的地物威胁,将这个威胁融合到原始地图中,得到了融合地形威胁的地形图8。图9是平滑后的地形图,对比图8和图9可以看出经过预处理后的地图要比之前平滑很多,没有了原始地形图锋利的边角,更适应对飞行器的航迹规划。图10是根据粒子群规划算法得到的三维航迹规划路径。图11是航路图的俯视图形,图12是航路的侧视图,综合图11和图12可以看出,该方法规划的航路既有威胁回避的部分又有地形跟随的部分,可满足实际应用要求。
4 结语
通过对地图的预处理,将静态威胁融合到数字地图中,根据飞行器的性能指标,详细给出了数字地图平滑处理手段和躲避威胁的方法。设计代价函数,运用粒子群算法在Matlab软件中编程,实现了飞行器执行任务前的三维航路图的规划,为飞行器在运行过程中对静态威胁的躲避提供了有利保障,在执行任务过程中只需要对离线规划的航路进行修改,节省了在线航迹规划的时间。
/References:
[1] 任鹏,高晓光.有限干预下的UAV低空突防航迹规划[J].系统工程与电子技术,2014,36(4):679-684.REN Peng,GAO Xiaoguang.Human intervention flight path planning for UAV low-altitude penetration[J].Systems Engineering and Electronics,2014,36(4):679-684.
[2] BABEL L.Flight path planning for unmanned aerial vehicleswith landmark-based visual navigation[J].Robotics and Autonomous Systems,2014,62:142-150.
[3] 叶文,朱爱红,刘博,等.飞机低空突防技术研究[J].电光与控制,2007,14(4):87-91.YEWen,ZHU Aihong,LIU Bo,etal.Research on low-altitude penetration technology of aircrafts[J].Electronics Optics & Control,2007,14(4):87-91.
[4] 陈侠,鹿振宇.基于不同地形的低空安全突防曲面处理算法[J].电光与控制,2013,20(5):1-5.CHEN Xia,LU Zhenyu.Processing algorithm for low-altitude penetration safety surface based on different types of terrain[J].Electronics Optics &Control,2013,20(5):1-5.
[5] KARIMIJ,POURTAKDOUSTS.Optimalmaneuver-basedmotion planning over terrain and threatsusing a dynamic hybrid PSO algorithm[J].Aerospace Science and Technology,2013,26:60-71.
[6] 李新胜,兰时勇,李纲,等.利用BéZier和B样条曲线模拟飞机航迹的方法[J].西南交通大学学报,2011,46(6):1040-1045.LIXinsheng,LAN Shiyong,LIGang,etal.Simulation of aircraft flight track by BéZier and B-spline curve[J].Journal of Southwest Jiaotong University,2011,46(6):1040-1045.
[7] 白晓利,韩亮.基于数字地图预处理的低空突防飞行路线规划[J].北京航空航天大学学报,2005,31(8):853-857.BAIXaioli,HAN Liang.Path planning for penetrating aircraft to fly at low altitudes based on technology of digital elevationmap[J].Journal of Beijing University of Aeronautics and Astronautics,2005,31(8):853-857.
[8] 薛锋,欧阳中辉,吴晓君.低空突防视景系统的三维建模与实时仿真[J].计算机工程,2005,31(6):168-170.XUE Feng,OUYANG Zhonghui,WU Xiaojun.3D modeling and real-time simulation of low-altitude penetration visualization system[J].Computer Engineering,2005,31(6):168-170.
[9] 贺也平,胡志忠,徐克虎,等.一种基于数字地图的轨迹优化算法的改进[J].数据采集与处理,1999,14(4):447-451.HE Yeping,HU Zhizhong,XU Kehu,et al.Improvement of digitalmap data based guidance algorithm[J].Journal of Data Acquisition & Processing,1999,14(4):447-451.
[10] 徐安,寇英信,于雷,等.基于仿真计算的飞行器雷达隐身性能评估[J].电光与控制,2011,18(9):22-26.XU An,KOU Yingxin,YU Lei,et al.Stealth performance assessment of low observable aircrafts based on simulation[J].Electronics Optics & Control,2011,18(9):22-26.
[11] 傅阳光,周成平,丁明跃.基于混合量子粒子群优化算法的三维航迹规划[J].宇航学报,2010,31(12):2657-2664 FU Yangguang,ZHOU Chengping,DINGMingyue.3D route planning based on hybrid quantum behaved particle swarm optimization[J].Journal of Astronautics,2010,31(12):2657-2664.
[12] MO H,XU L.Research of biogeography particle swarm optimization for robot path planning[J].Neurocomputing,2015,148:91-99.
[13] 陈攀峰,刘文军,王为.基于粒子群算法的无人机航迹规划[J].电子设计工程,2013,21(22):36-39.CHEN Panfeng,LIUWenjun,WANGWei.Route planning of UAV based on particle swarm optimization(pso)algorithm[J].Electronic Design Engineering,2013,21(22):36-39.
[14] 郭淳芳.一种新的机器人自组网络群组运动控制模型[J].河北工业科技,2012,29(6):411-414.GUOChunfang.A novel groupmovementcontrolmodel for the Ad hoc robotnetwork[J].Hebei Journal of Industrial Science and Technology,2012,29(6):411-414.
[15] ESPELOSIN J,ACOSTA L,ALONSO D.Path planning approach based on flock dynamics ofmoving particles[J].Applied Soft Computing,2013,13:2159-2170.
[16] 汪雷,刘欣,杨涛,等.高超声速滑翔式飞行器目标覆盖范围的计算方法[J].弹道学报,2014,26(1):50-55.WANG Lei,LIU Xin,YANG Tao,et al.Footprint calculation for hypersonic glide vehicle[J].Journal of Ballistics,2014,26(1):50-55.
[17] WU G,QIU D,YU Y,et al.Superior solution guided particle swarm optimization combined with local search techniques[J].Expert Systems with Applications,2014,41:7536-7548.
[18] 吕晋,张俊,王南.移动机器人模块化机械臂运动学分析[J].河北工业科技,2013,30(5):333-337.LYU Jin,ZHANG Jun,WANG Nan.Kinematics analysis ofmodularmanipulators ofmobile robot[J].Hebei Journal of Industrial Science and Technology,2013,30(5):333-337.
[19] TSAIH,LAIY,LO S.A zero-watermark scheme with geometrical invariants using SVM and PSO against geometrical attacks for image protection[J].The Journal of Systems and Software,2013,86:335-348.
[20] KUNDU R,DASS,MUKHERJEE R,et al.An improved particle swarm optimizer with differencemean based perturbation[J].Neurocomputing,2014,129:315-333.
[21] UNLER A,MURAT A,CHINNAM R.mr2PSO:A maximum relevanceminimum redundancy feature selection method based on swarm intelligence for support vectormachine classification[J].Information Sciences,2011,181(20):4625-4641.
