一种离散变结构组合控制策略在UUV舵机系统中的应用

潘元璋 赵龙龙

(91388部队93分队 湛江 524022)



一种离散变结构组合控制策略在UUV舵机系统中的应用

潘元璋 赵龙龙

(91388部队93分队 湛江 524022)

对离散变结构控制理论中的离散趋近律方法进行研究,提出一种新的可期待原点稳定性的趋近律—离散变速趋近律,其特点是与系统状态范数成正比,并能够产生扇形切换区。以变速趋近律和传统趋近律为基础,形成一种具有良好性能的组合控制策略。将该组合控制策略应用于UUV舵机系统的无刷直流伺服电机的控制,仿真结果表明,无论是否存在外部扰动的影响,所设计的控制器对给定位置信号都具有很强的跟踪能力。

变结构控制; UUV; 舵机; 无刷直流伺服电机

Class Number U226.8

1 引言

变结构控制具有对参数摄动和外部干扰不变性的优点。连续系统的变结构控制已得到广泛研究,建立了较为完整的理论体系,并在工程领域的应用研究方面也取得了丰硕成果。但是,当采用计算机实现变结构控制算法时,采样间隔的存在将导致沿切换面的抖振现象,甚至使系统变得不稳定。因此,直接基于离散时间系统的变结构控制研究具有重要意义。在高为炳提出离散趋近律方法[1]之前,曾经出现过三种不等式形式的到达条件[2～4]为

[s(k+1)-s(k)]s(k)<0

(1)

(2)

(3)

1995年,高为炳提出了指数趋近律的离散形式[5],可表示为

s(k+1)=(1-qT)s(k)-Tεsgn(s(k))

(4)

其中T为采样周期,ε>0;q>0;qT<1。在所有这些到达条件中,高为炳的理论较为完备,在揭示离散变结构控制系统的运动机理方面前进了一大步。然而,离散指数趋近律式(4)自身也存在一些不足,即:在切换区里面,系统运动轨迹为步步穿越切换面的等幅运动,系统状态轨迹最终将趋于原点附近的某个抖动[1,6],而不是稳定于原点,因此,控制系统的稳态精度不理想。

本文提出了一种新形式的离散趋近律,即变速趋近律,它可以期待原点的稳定性。与指数趋近律相比,变速趋近律的最大优点在于能够保证受控系统具有更好的稳态精度。将指数趋近律和变速趋近律结合起来,可以形成一种组合控制策略,从而能够克服两种趋近律的不足,保留它们的优点。将提出的组合控制策略用于UUV舵机系统的无刷直流伺服电动机的控制,仿真结果验证了理论结论的正确性。

2 离散趋近律

离散趋近律,实质上就是能够刻画切换函数s(k)的动态的差分方程,这种渐近稳定的差分方程本身就是一种到达条件。另外,通过对趋近律方程中的参数进行选择,可以使变结构控制系统在趋近模态段的动态品质得到保证。离散趋近律法的最大优点在于使变结构控制律的获取变得非常简单。考虑如下的离散时间系统[7]:

x(k+1)=Ax(k)+bu(k)

(5)

式中,x∈Rn,u∈R,(Ab)可控。采用线性切换函数:

s(x)=cx(k)

(6)

其中c的选择应满足cb≠0。适当选择切换函数系数矩阵c中各元素的值,即可保证准滑动模态运动具有渐近稳定性和良好的动态品质。由式(5)、式(6)可得:

s(k+1)=cAx(k)+cbu(k)

(7)

令式(7)与指数趋近律到达条件(4)右端相等,可得:

cAx(k)+cbu(k)=(1-qT)s(k)-εTsgn(s(k))

(8)

则由式(8)即可解出离散变结构控制律:

u=u±(k)= -(cb)-1[cAx(k)-s(k)

+qTs(k)+εTsgn(s(k))]

(9)

3 变速趋近律

在前人的基础上,提出如下形式的离散变速趋近律[8～9]:

s(k+1)=s(k)-εT‖x(k)‖1sgn(s(k))

(10)

在二阶系统中,s=±εT‖x(k)‖1是过原点的射线,切换线s=0夹在其中。可见,变速趋近律的切换区是厚度为2Δ=2εT‖x(k)‖1的扇形,系统的稳态为原点,如图1所示。由式(7)、式(10)可求出以变速趋近律为到达条件的离散变结构控制律:

u(k)= -(cb)-1[cAx(k)-cx(k)

+εT‖x(k)‖1sgn(cx(k))]

(11)

与指数趋近律的带状切换区、只能稳定于原点邻域的某个抖动状态[10]相比,变速趋近律的优点是具有良好的稳态性能,可以期待原点的稳定性。但变速趋近律也存在缺点:由于引入了状态范数,系统穿越切换面的幅度与‖x(k)‖1成正比,当‖x(k)‖1的值比较大时,穿越幅值也很大,因此,在系统刚进入切换区的那一段,可能产生大幅度的穿越抖动,使动态性能变差,如图2(b)所示。

图1 变速趋近律的切换区

4 组合控制策略

通过上面的分析研究,不难发现,如果把离散指数趋近律式(4)与离散变速趋近律式(10)结合起来使用,即在趋近模态段和滑动模态段的前期采用指数趋近律决定的控制律式(9),而在滑动模态段的后期和稳态段采用变速趋近律决定的控制律式(11),则可以克服两种趋近律的缺点,保留它们的优点,从而使系统性能达到最好。两种控制律转换点的选择可由下式确定:

εT=εT‖x(k)‖1

(12)

于是,可得如下的组合控制策略:

(13)

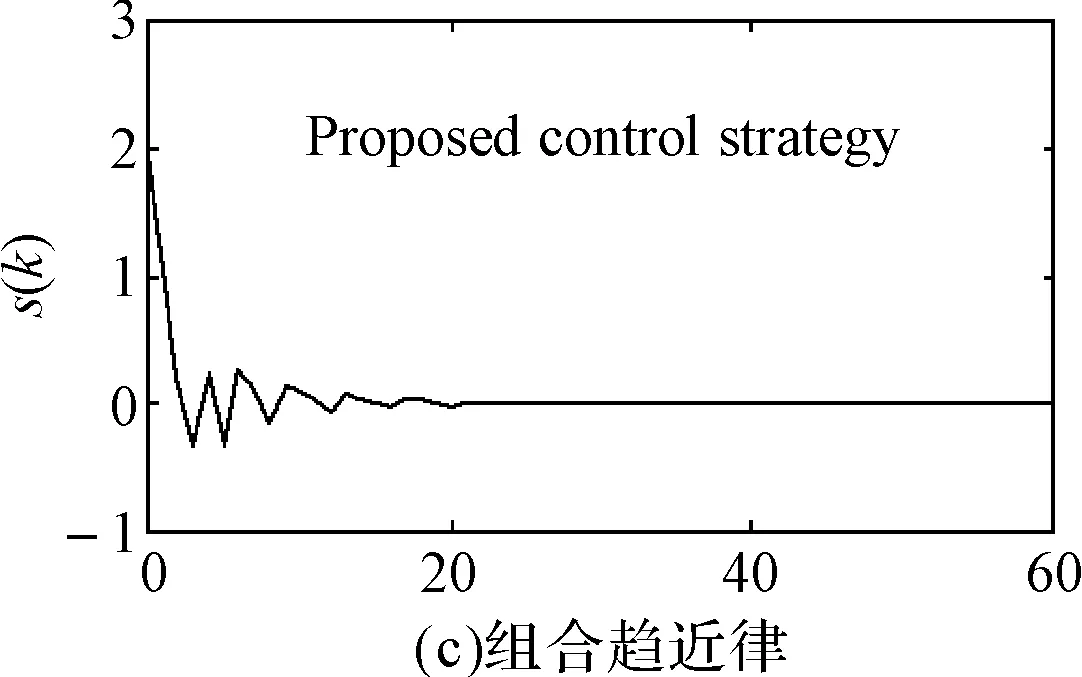
图2 不同趋近律的动态特性

5 应用于UUV舵机直流伺服系统

图3显示了采用离散变结构控制器的UUV舵机直流伺服系统方框图。图中Ks为PWM功率放大器的放大倍数;R为电枢回路总电阻;T1为电枢回路电磁时间常数;Jm为折算到电动机轴上的转动惯量;Cm、Ce分别为电动机在额定磁通下的转矩常数和电势常数;Id、Ifz分别为电枢电流和负载电流;ω、θ分别为电动机的角速度和角位移;E为电动机的反电动势。则由图3可以写出参数表达式:

(14)

(15)

(16)

其中θr、ωr分别表示位置给定和速度给定,则可得系统状态方程:

(17)

其中,

对式(17)离散化,可得:

x(k+1)=Ax(k)+Bu(k)+DIfz(k)

(18)

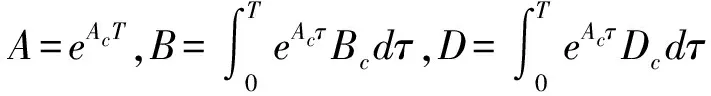
在控制器设计中,负载电流Ifz处理为外部干扰。

图3 直流伺服系统结构图

设给定角位移信号为幅值为1的阶跃信号,标称参数时直流伺服系统的仿真曲线如图4所示。图5则为同时存在参数摄动和负载干扰时的仿真结果。由图可见,无论是否存在不确定性,本文设计的离散变结构控制器都可以使伺服系统快速准确地跟踪给定信号,体现了变结构控制器鲁棒性强的优点。

图4 存在参数摄动和负载干扰时的仿真结果

6 结语

本文提出的离散变速趋近律可以产生扇形切换区,能够期待原点的稳定性。将它与指数趋近律组合使用,可以克服指数趋近律稳态为抖动的缺点,使离散趋近律方法更加完善。将所提方法用于UUV舵机系统的无刷直流伺服电机的控制,仿真研究结果表明了它的有效性。

[1] W. Gao, Y. Wang, A. Homaifa. Discrete-time variable structure control systems[J]. IEEE Trans. Ind. Electron,1995,42:117-122.

[2] Y. Dote, R. G. Hoft. Microprocessor based sliding mode controller for dc motor drives[J]. IAS Annual Meeting, Cincinnati: OH,1980.

[3] S. Z. Sarpturk, Y. Istefanopulos, O. Kaynak. On the stability of discrete-time sliding mode control systems[J]. IEEE Trans. Automat. Contr.,1987,32:930-932.

[4] K. Furuta. Sliding mode control of a discrete system[J]. Syst. Contr. Lett.,1990,14:145-152.

[5] 云飞,刘金混,王宗学.一种离散变结构控制方法在伺服系统中的应用[J].机床与液压,2002(2):31-33.

[6] 周德文,高存臣,李自强.一种离散变结构控制趋近律[J].控制与决策,2008,23(3):306-310.

[7] 朱齐丹,吕开东,李新飞,等.一种基于改进趋近律的离散变结构控制方法[J].系统工程与电子技术,2012,34(6):1211-1215.

[8] Yao Qionghui, Song Lizhong, Wen Hong. Proportional-constant-variable rate control for discrete-time variable structure systems[J]. Control & Decision,2000,15(3):329-332.

[9] 李忠娟,张新政,李晓昱.一种改进的离散时间系统变结构控制[J].电机与控制学报,2005,9(1):90-94.

[10] Gao Weibing. Variable structure control theory and design procedures[M]. Beijing: Press of Science,1998.

An Discrete Varistructure Composite Control Strategy Apply to UUV’s Steering Gear System

PAN Yuanzhang ZHAO Longlong

(Unit 93, No. 91388 Troop of PLA, Zhanjiang 524022)

Research on discrete method of approach included in discrete varistructure control theories is conducted. A kind of new method of approach named discrete variable speed approachable law which could expect origin stabilize is proposed, whose features include directly proportional with system norm and making fan-shaped areas created. A composite control strategy with good performance is formed based on variable speed method of approach and traditional method of approach. The combinatorial control strategy is applied to brushless DC servo motor included in UUV’s steering gear system, analysis of simulation result indicates that the designed controller has almighty tracking ability to given position signal.

varistructure control, UUV, steering machine, brushless DC servo motor

2015年1月14日,

2015年2月15日 作者简介:潘元璋,男,硕士,助理工程师,研究方向:水下靶标技术。赵龙龙,男,硕士,高级工程师,研究方向:水下靶标技术。

U226.8

10.3969/j.issn1672-9730.2015.07.023