应用频谱图的机织物纹理分析
2015-03-10李立轻
薛 乐,李立轻,2,3,汪 军,2
(1.东华大学纺织学院,上海 201620;2.东华大学纺织面料技术教育部重点实验室,上海 201620;3.东华大学产业用纺织品教育部工程研究中心,上海 201620)
应用频谱图的机织物纹理分析
薛 乐1,李立轻1,2,3,汪 军1,2
(1.东华大学纺织学院,上海 201620;2.东华大学纺织面料技术教育部重点实验室,上海 201620;3.东华大学产业用纺织品教育部工程研究中心,上海 201620)
利用傅里叶变换技术将空间域的纹理图像变换到频率域中,采用频谱图对机织物纹理信息进行分析。通过傅里叶变换技术得到机织物图像的频谱图,利用阈值分割曲线选取合适的阈值对频谱图进行分割,然后用邻域最大值的方法找到织物纹理的特征坐标点。根据坐标点与实际频率的关系计算机织物纹理的频率范围。实验结果表明,随着密度的增大织物纹理的频率增加,斜纹和缎纹的频率范围比平纹织物的大,常见机织物的纹理为中低频。
图像处理;傅里叶变换;织物纹理;频率
纹理是物体表面信息的反映,以彩色或灰度图像的分布形式反映了不同物体基本的视觉特征。纹理分析技术广泛应用于人脸识别、图像检索、遥感图像分析、医学图像处理等方面。机织物是由经纱和纬纱按照一定规律垂直交织而成的,其纹理呈现出一定的周期性。
李静等[1]用灰度共生矩阵对织物试样进行纹理分析,提取不同方向的特征参数来表征织物试样的纹理特征。祝双武等[2]用自相关函数的方法得到纹理基元模板来表征织物纹理,然后利用纹理基元与基元模板间的差,突出疵点信息进行疵点检测。Ajay Kumar等[3-4]用 Gabor变换分析织物纹理,并提取特征值对织物疵点进行检测。姚芳等[5]用自适应小波对纹理图像进行特征提取,并将这种方法应用于织物疵点检测。
在对织物起毛起球和织物褶皱的自动等级评定、织物疵点检测以及图像分割的分析中,织物纹理的基础分析起着关键的作用。傅里叶变换的频谱能够反映图像的周期性和方向性信息,也能够反映图像纹理的粗糙度。辛斌杰等[6-7]采用傅里叶变换对织物组织结构和织物密度进行了分析。本文利用傅里叶变换技术将空间域的纹理图像变换到频率域中,采用频谱图对机织物纹理信息进行分析。
1 傅里叶变换原理
傅里叶变换可将纹理信息从空间域转换到频率域,利用频谱图的能量分布分析织物纹理。图像是由颜色或灰度组成的二维离散数据矩阵,对它进行频域转换的方法是离散傅里叶变换。
令f(x,y)表示一幅大小为M×N图像中(x,y)的灰度,则f(x,y)的二维离散傅里叶变换为

式中 u=0,1,2,…,M -1;v=0,1,2,…,N -1,其逆变换为

式中 x=0,1,2,…,M -1;y=0,1,2,…,N -1。
2 织物频率信息提取的方法
2.1 基于快速傅里叶变换的频谱图
对尺寸为 512像素 ×512像素,分辨率为600 dpi的机织物图像进行快速傅里叶变换,得到频谱图,如图1、2所示。机织物频谱图为明暗不一的亮点,中心点代表图像的低频信息,其余亮点(特征坐标点)代表周期性结构的频率成分即织物经纬纱纹理,随机点(雪花状背景点)代表周期性不是很强的频率信息。

图1 织物图像Fig.1 Fabric image

图2 频谱图Fig.2 Spectrum image
2.2 特征坐标点的提取
首先去除图像中心的最亮点(原点),然后选取合适的阈值消除雪花状背景点,如果图像中某像素的灰度值大于该阈值则该像素的灰度值不变,否则灰度值设为0,结果如图3所示。令g(x,y)为原始图像傅里叶变换后的频谱图,阈值分割后的频谱图定义为


图3 阈值分割后频谱图Fig.3 Spectrum after threshold segmentation
常见的阈值选取方法包括:迭代法、OTSU法、一维最大熵法和双峰法,但由于图像的差异,因此没有一种方法适合所有的图像。辛斌杰等[6]通过观察功率谱图的灰度分布,取最高点的灰度值做为阈值。王庆涛等[7]通过大量的阈值选取,得到阈值分割曲线,并根据曲线得到织物图像的动态阈值。
本文首先作出织物图像的三维频谱图,如图4所示,图像以原点为中心对称分布着明显的峰值。观察三维频谱图,人工选取合适的阈值对频谱图进行分割。通过20幅织物图像的阈值选取实验,发现对每幅图像采用T=0.5×Tmean+0.5×Tmax(Tmean为三维频谱图幅值的均值,Tmax为三维频谱图幅值的最大值)得到的阈值能替代人工选取阈值的方法。
2.3 峰点滤波

图4 三维频谱图Fig.4 Three dimensional spectrum image
阈值分割后的频谱图存在亮点集中的区域,在计算织物的实际频率时会大大增加计算量。峰点是某个局域内灰度值最高的像素点,因此可以用邻域最大值的方法确定峰点。根据图像的大小与亮点的分布情况,令T'max为阈值分割后频谱图g(x,y)的32×32区域内的最大值,则:

峰点滤波后的图像如图5所示。为了显示清楚,图中每个亮点表示以峰点为圆心,16邻域内的多个像素点。
2.4 基于图像的机织物频率的计算

图5 峰点滤波后频谱图Fig.5 Spectrum after peak filtering

为了分析不同分辨率的织物图像,统一对纹理进行表征,本文对织物纹理的频率进行如下定义:式中:F为频谱图频率表示每毫米的周期数;d为频谱图中某个峰点与中心点的距离;r为图像的分辨率;D为频谱图上的点与中心点的最大距离,D=(M/2)2+(N/2)2,M和N分别为织物图像的经向像素数和纬向像素数。
2.5 织物的频谱图像处理
对织物图像进行FFT变换得到频谱图,根据阈值分割曲线选取合适的阈值,保留表征织物纹理的特征坐标点,通过峰点滤波确定峰点,计算纹理的频率范围。本文对斜纹和缎纹进行了分析,结果如图6所示。

图6 织物处理流程图Fig.6 Fabric and spectra.(a)Twill fabric image;(b)Twill spectrum image;(c)Twill spectrum after threshold segmentation;(d)Twill spectrum after peak filtration of twill fabric;(e)Satin fabric image;(f)Satin spectrum image;(g)Satin spectrum after threshold segmentation;(h)Satin spectrum after peak filtration of satin fabric
3 机织物纹理与频率关系分析
频谱图中有规律的亮点代表周期性明显的纹理,随机点代表杂质或噪声,因此通过提取亮点信息可以将纹理和疵点分离,有利于检测疵点[8]。根据傅里叶逆变换的特性,验证了通过上述方法选取的亮点代表了织物的纹理信息,然后根据不同亮点代表的具体含义讨论了频率的影响因素,通过对多幅织物图像的分析,得到了织物纹理的频率范围。
本文实验所用织物为20块不同规格的素色织物(平纹10块、斜纹6块、缎纹4块);图像是分辨率为600 dpi,尺寸为512像素×512像素的灰度图像。
3.1 织物纹理信息的确定
将仅保留亮点区域的频谱图进行傅里叶逆变换,如图7(d)~(f)所得到的图像仅保留了织物的纹理信息;将频谱图的亮点区域消除后,进行傅里叶逆变换,如图7(g)~(i)的原图像的纹理信息被消除,则选取的亮点区域代表了织物的纹理信息。

图7 傅里叶逆变换Fig.7 Inverse Fourier transform.(a)Plain fabric;(b)Twill fabric;(c)Satin fabric;(d)Plain inversion after highlights preservation;(e)Twill inversion after highlights preservation;(f)Satin inversion after highlights preservation;(g)Plain inversion after highlights elimination;(h)Twill inversion after highlights elimination;(i)Satin inversion after highlights elimination
3.2 图像分辨率对频率的影响
将不同分辨率的图像进行傅里叶变换得到频谱图,如图8所示。频谱图关于原点对称,不同分辨率的频谱图分布规律一致,随着图像分辨率增加,频谱图最亮点与原点距离减小。本文用最亮点的频率分析分辨率对频率的影响,根据式(5)计算相同织物不同分辨率(300、600、900 dpi)图像的频谱图中最亮点的频率,结果相同,所以分辨率对频率无影响。
3.3 织物密度对频率的影响

图8 不同分辨率的织物图像及频谱图Fig.8 Fabric images of different resolutions and corresponding spectra.(a)300 dpifabric;(b)600 dpi fabric;(c)900 dpi fabric;(d)300 dpi frequency spectrum;(e)600 dpifreqaency spectrum;(f)900 dpifrequency spectrum
织物的频谱图中,在中心处的不同方向都存在较亮的点,其中接近水平和垂直方向的亮点代表经纬向的频率[9],如图9、10所示。将20块织物按经纬密排列,经纬密和频率之间是线性关系,从图中可以看出,随着经纬密的增大,经纬向频率增大,这是因为密度增加,纱线间排列紧密,图像的灰度梯度大,频谱图中的亮点与中心距离增加。

图9 经密和经向频率的关系图Fig.9 Relationship between warp density and frequency
3.4 织物纹理的频率范围
织物是由经纱和纬纱按照一定规律垂直交织而成,平纹织物的主纹理在水平或垂直轴上,斜纹和缎纹的主纹理不在轴上,而是有一定的角度[10]。织物纹理的最低频率对应距离中心点最近的点,最高频率对应距中心点最远的点。图11、12分别示出3种织物密度和频率的关系。图11、12中横坐标为织物经纬密的平方和的根,纵坐标为织物纹理的频率范围,竖线长度为每幅织物纹理的频率范围,圆圈所示为图像最亮点的频率。

图10 纬密和纬向频率的关系图Fig.10 Relationship between weft density and frequency
图11为平纹织物密度与频率的关系图,代表织物主要纹理的最亮点在水平或垂直线上,处于最低频率和最高频率之间。图中密度为400和450根/10cm附近的3块织物,由于经纬密度相差较大,所以最亮点处于密度最小位置附近。图12为斜纹和缎纹织物密度与频率的关系图。可以看出最亮点频率为最低频率或接近最低频率,这是因为斜纹和缎纹的纹理有一定角度的方向性,最亮点频率对应织物主对角线上最接近中心点的点。这也是相同经纬密度下,斜纹和缎纹的最亮点频率比平纹低的原因。
从图11、12中可以看出,1)随着密度的增大织物纹理的频率增加;2)斜纹和缎纹纹理的频率分布范围比平纹织物的大,斜纹和缎纹为3~6次/mm,平纹为2~3次/mm;3)常见机织物的纹理频率为中低频,范围为2~8次/mm。
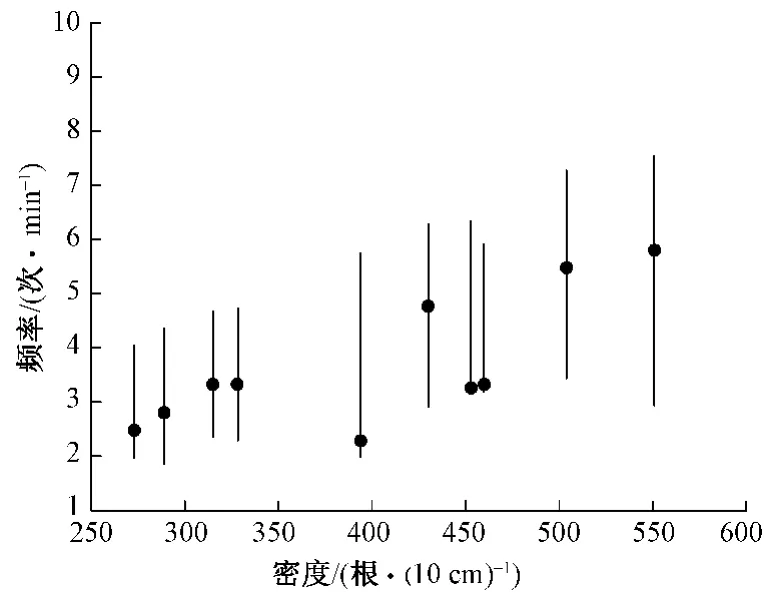
图11 平纹织物密度和频率的关系Fig.11 Relationship between plain density and frequency

图12 斜纹和锻纹织物密度和频率的关系Fig.12 Relationship between twill and satin density and frequency
4 结论
本文通过大量的阈值选取实验,找到了一条阈值分割曲线可以有效地消除频谱图雪花状背景点,找到表征织物纹理的特征坐标点。进而通过计算最亮点的频率,得出分辨率对织物纹理频率无影响。根据经纬向的频率,得出经纬向频率随着经纬密度的增加而增大。最后分析了平纹、斜纹和缎纹最亮点频率与频率范围的关系,并分别给出平纹、斜纹和缎纹的纹理频率范围。
[1] 李静,杨玉倩,沈伟,等.基于灰度共生矩阵的织物纹理研究[J].现代纺织技术,2013(3):12-16.LI Jing,YANG Yuqian,SHEN Wei,et al.Research on fabric texture based on gray level co-occurrence matrix[J].Advanced Textile Technology,2013(3):12-16.
[2] 祝双武,郝重阳.基于纹理周期性分析的织物疵点检测方法[J].计算机工程与应用,2012,48(21):163-166.ZHU Shuangwu, HAO Chongyang. Fabric defect detection approach based on texture periodicity analysis[J].Computer Engineering and Applications,2012,48(21):163 -166.
[3] AJAY Kumar, GRANTHAM K H Pang. Defect detection in textured materials using Gabor filters[J].IEEE Transactions on Industry Applications, 2002,38(2):425-440.
[4] LIU Yanbei,XIAO Zhitao,ZHANG Fang.Fabric defect detection method based on Gabor filters[J].Advanced Material Research,2011,301 -303:229 -234.
[5] 姚芳.织物纹理的表征和自动识别的研究[D].上海:东华大学,2010:29-42.YAO Fang.Study on fabric texture representation and automatic identification[D]. Shanghai:Donghua University,2010:29 -42.
[6] 辛斌杰,余序芬,吴兆平.应用图像分析技术自动识别织物的组织结构[J].东华大学学报:自然科学版,2011,37(1):35 -41.XIN Binjie, YU Xufen, WU Zhaoping. Automatic identifying the woven fabric pattern by image analysis technique[J].Journal of Donghua University:Natural Science Edition,2011,37(1):35 -41.
[7] 王庆涛,马崇启,高雨田,等.基于频域特征点提取的素色机织物密度识别算法[J].纺织学报,2014,35(4):47-51.WANG Qingtao,MA Chongqi,GAO Yutian,et al.Identification algorithm of plain woven fabric density via feature point extraction in frequency domain[J].Journal of Textile Research,2014,35(4):47 -51.
[8] XU Bugao. Identifying fabric structures with Fast Fourier Transform Techniques[J].Textile Research Journal,1996,66(8),496 -506.
[9] 孙亚锋,陈霞,王新厚.机织物密度的计算机自动识别[J].东华大学学报:自然科学版,2006,32(2),83-88.SUN Yafeng,CHEN Xia,WANG Xinhou.Automatic recognition of the density of woven fabrics[J].Journal of Donghua University:Natural Science Edition,2006,32(2):83-88.
[10] 管声启.方向性纹理织物疵点检测方法研究[J].计算机工程与科学,2011,33(3),73 -76.GUAN Shengqi.A detection method of directional texture fabric defects[J].Computer Engineering &Science,2011,33(3),73 -76.
Study on woven fabric texture using frequency spectrum
XUE Le1,LI Liqing1,2,3,WANG Jun1,2
(1.College of Textile,Donghua University,Shanghai 201620,China;2.Key Laboratory of Textile Science &Technology,Ministry of Education,Donghua University,Shanghai201620,China;3.Engineering Research Center of Technical Textiles,Ministry of Education,Donghua University,Shanghai 201620,China)
In order to analyze the texture information of woven fabric,the woven fabric image was converted from the spatial domain to the frequency domain using the Fourier transform.The spectrum of the woven fabric was obtained by using the Fourier Transform method.The appropriate threshold was selected from the threshold segmentation curve to segment the spectrum and the feature points containing the fabric texture were found by the maximum of neighborhood method.Based on the relationship between the feature points and the real frequency,the frequency range of woven fabric texture was obtained.The experiment result shows that the frequency of fabric texture increase with the increase of density and the frequency range of twill and satin is larger than the plain weave and the frequency of common woven fabric texture is low and medium.
image processing;Fourier transform;fabric texture;frequency
TS 101.9
A
10.13475/j.fzxb.20140702806
2014-07-14
2014-11-18
国家自然科学基金资助项目(61271006,61379011);中央高校基本科研业务费专项资金资助(14D110130)
薛乐(1988—),女,硕士生。主要研究方向为数字化纺织品。李立轻,通信作者,E-mail:liliqing@dhu.edu.cn。
