应用CHES-FY系统的织物硬挺度测试

孙 草，杜赵群

(东华大学纺织面料技术教育部重点实验室，上海 201620)

织物硬挺度为织物的基本风格之一，是决定织物造型美和消费者喜好的关键指标之一，如西服的挺括、针织内衣的贴身柔软、非织造布的硬挺等。织物硬挺度的客观实验测试［1－3］可有效评价其使用，如皮革类非织造布的硬挺度测试能更好地指导其在服用、家纺上的应用，针织物测试可以使其在内衣上达到更好的舒适度，机织物测试使其在西服、西裤等选材上更具指导意义。

织物硬挺度风格的测试方法常见的为KES、FAST、PhabrOmeter等［4－6］，以上基本上为小应力下的织物硬挺度定量测试，对于非织物、大衣等硬挺试样的测试就变得较为困难，且分析繁琐、仪器价格昂贵，而未能得到广泛应用，因此，国内外企业所常采用简易的斜面法测试仪分析织物硬挺度［4］，依据标准GB/T 18318.1—2009《纺织品 弯曲性能的测定第1部分:斜面法》和GB/T 18318.2—2009《纺织品弯曲性能的测定第2部分:心形法》。该方法测试简易，成本低，但织物试样制备过程中一端由于拆纱差异对结果影响较大，对刚硬的非织物和柔软的针织物而言其测试亟待解决;基于此类原理的心形法测试织物的硬挺度，是将织物弯成心形形状，测试弯曲刚度和长度，但对于柔软织物而言，造型接近，分辨率低。

据此，本文基于纺织品性能测试仪(CHES-FY)对织物硬挺度进行测试［7－8］，探索其在测试织物柔软硬挺度方面的实用性，选用针织布、机织布、非织造布和复合材料等柔软、硬挺显著差异，测试指标值为宽范围的试样进行测试，并与斜面法和心形法进行对比测试，验证该系统测试的可适性。

1 实验部分

1.1 CHES-FY系统弯曲性能测量基本原理

CHES-FY系统及主要机构［9］如图1(a)所示，由托针、双U形针、夹头、主机和控制器构成。实验时将试样夹持在夹头上，由托针完成试样的抽拔。

托针抽拔织物的抽拔力由与托针相连的力传感器获得，抽拔距离由托针移动速度和采样频率计算获得，所得抽拔力-位移曲线如图1(b)所示。根据织物的抽拔变形形态与抽拔力-位移曲线形态，可知曲线特征值与织物的弯曲性能存在相关性。原因在于试样在抽拔过程中存在弯曲变形，当托针托起试样至双U形针间的织物试样为水平直线形态，托针和双U形针构成三点梁结构［10］对试样实施弯曲变形，为弯曲阶段的开始位置，终止于抽拔力达到最大力值开始下降位置。可从弯曲阶段的抽拔力-位移曲线提取左斜率k、峰值力Y和左面积S，因此，左斜率、峰值力和左面积用于CHES-FY系统评价织物的弯曲性能。

实验样品规格:机织物经纬向尺寸分别为200mm×20mm;针织物、非织造布、复合材料尺寸为200mm×20mm。所有试样在温度为(20±2)℃，湿度为(65±3)%的条件下平衡24 h。实验测试中的仪器参数设置为:定夹头距离60mm，夹头到双压针的距离60mm，压针直径2mm，压针间距离10mm。

1.2 斜面法实验

根据斜面法弯曲性能测试标准(如图2所示)，将矩形试样放在水平平台上，试样长轴与平台长轴平行，沿平台长轴方向推进试样，使其伸出平台并在自重下弯曲，伸出端悬空，由尺子压住平台上试样的另一部分。当试样的头端通过平台的前缘达到与水平线呈41.5°倾角斜面时，可得弯曲长度。

图1 CHES-FY系统示意图和典型曲线图Fig.1 System diagram of CHES-FY system and typicalcurve.(a)System diagram of CHES-FY system;(b)Typical pulling-out force＆displacement curve

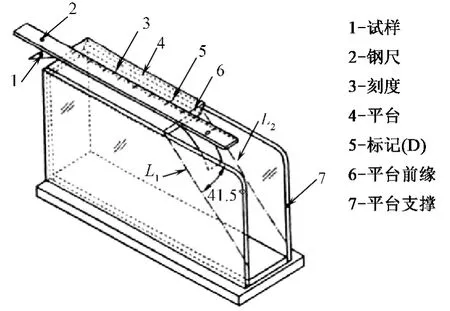
图2 斜面法示意图Fig.2 Schematic of Cantilever bending meter

实验样品规格:机织物经、纬向尺寸分别为250mm×25mm;针织物、非织造布、复合材料尺寸为250mm×25mm。所有试样在温度为(20±2)℃、湿度为(65±3)%的条件下平衡24 h。

1.3 心形法

心形法测试原理如图3所示，把长方形试样两端反向叠合后夹在试验架上，试样呈心形悬挂，测定心形环的高度，依此评定织物的弯曲性能。

图3 心形法试样及试样夹持Fig.3 Schematic diagram of Heart Loop test

实验样品规格:机织物经、纬向尺寸分别为250mm×20mm;针织物、非织造布、复合材料尺寸为250mm×20mm。所有试样在温度为(20±2)℃，湿度为(65±3)%的条件下平衡24 h。

1.4 织物试样规格

实验共选择20块织物试样，其中1号～3号为非织造布，4号为复合材料，5号和6号为针织布，7号为超高分子量聚乙烯纤维布，8号～20号为机织布。试样的厚度和面密度如表1所示。

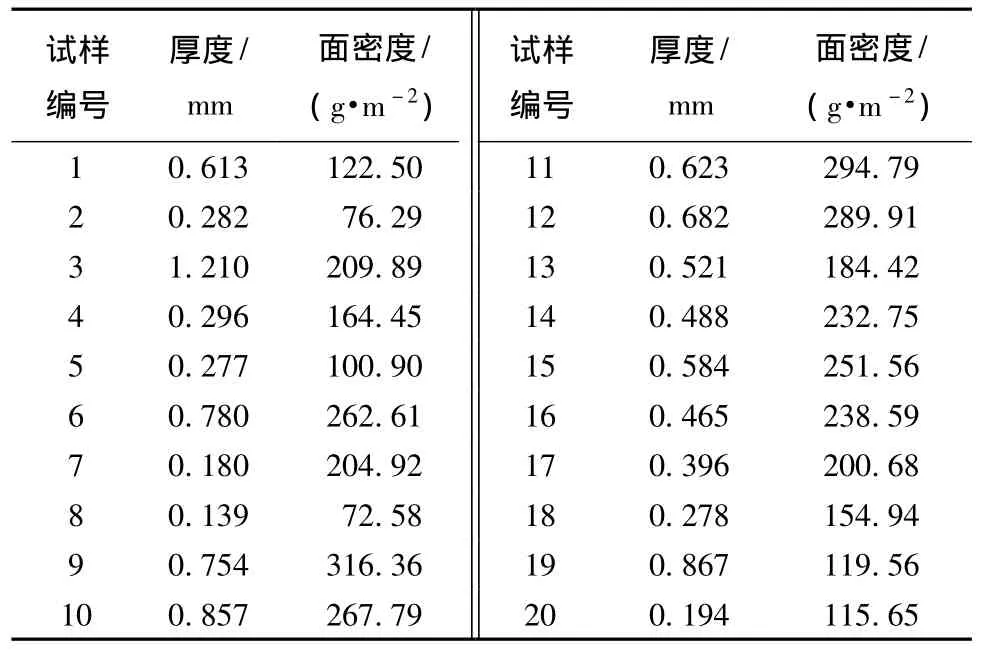
表1 20种试样的规格Tab.1 Specifications of 20 samples

2 结果与分析

2.1 测试结果分析

分别采用CHES-FY系统、斜面法、心形法对织物进行弯曲性能测试，测试结果如表2所示。从表2的测试结果可知:由于1号试样很硬，伸出的长度超过仪器范围，故斜面法对1号试样无法进行测试;心形法测试的弯曲长度数值很接近，由于误差的存在可能无法进行弯曲性能测试。而CHES-FY系统能测试上述20种试样，且测试指标结果对于柔软和硬挺的织物存在明显差异，较斜面法和心形法而言，可清晰地表达织物弯曲硬挺度的差异。

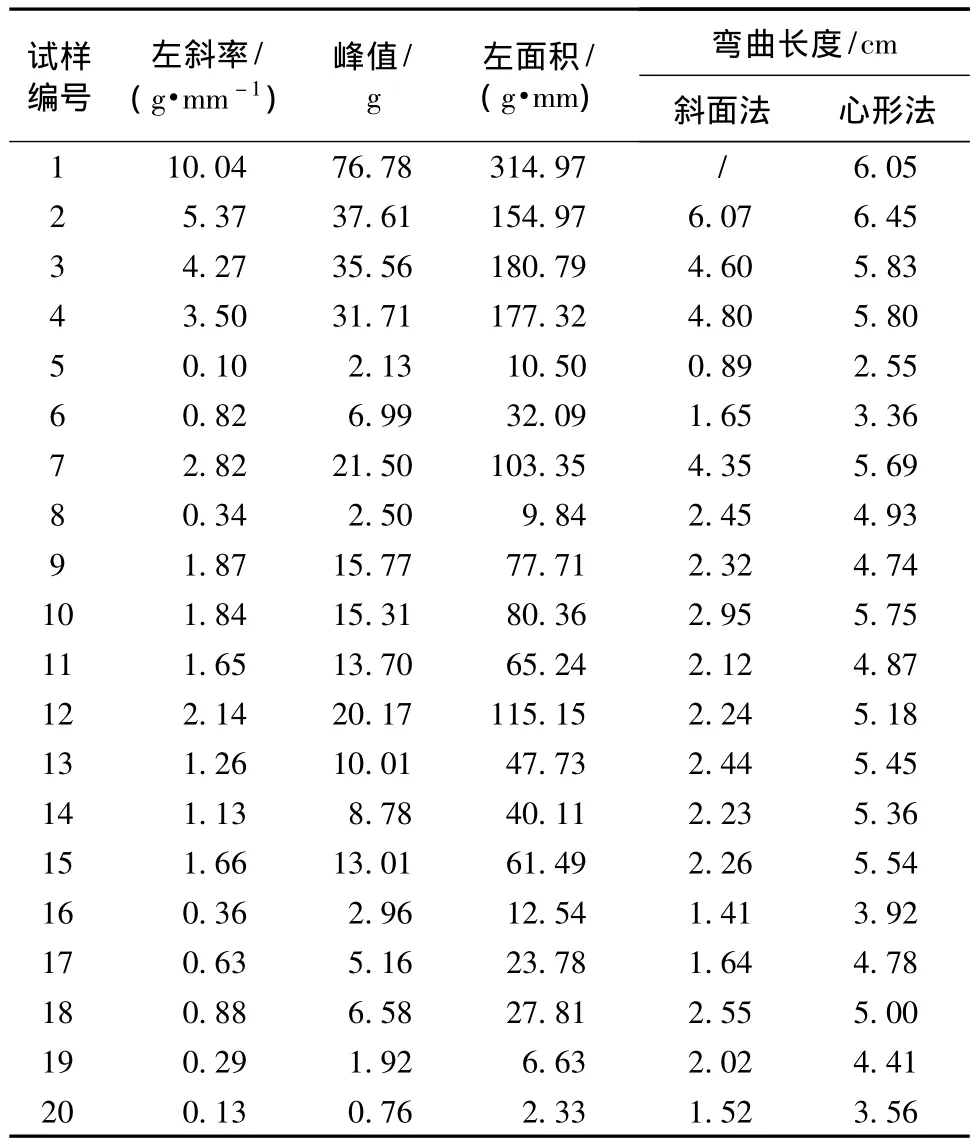
表2 20种试样的测试结果Tab.2 Experimental results of 20 samples

2.2 CHES-FY系统测试与斜面法相关性

基于对CHES-FY系统测试的实验分析，首先分别作每个变量与织物斜面法的弯曲长度的线性回归分析，结果如图4～6所示。可以看出，3个变量与织物斜面法的弯曲长度L之间有较好的线性关系。分析三者与斜面法弯曲长度的相关性知，三者与斜面法的相关系数分别为 0.934、0.905、0.858，说明用CHES-FY系统测试与斜面法的弯曲长度有较好的相关性，CHES-FY系统可准确地测量织物的弯曲性能。

图4 左斜率k与斜面法弯曲长度的线性回归分析Fig.4 Linear regression analysis of left slope k and bending length of Cantilever test

图5 峰值Y与斜面法弯曲长度的线性回归分析Fig.5 Linear regression analysis of peak Y and bending length of Cantilever test

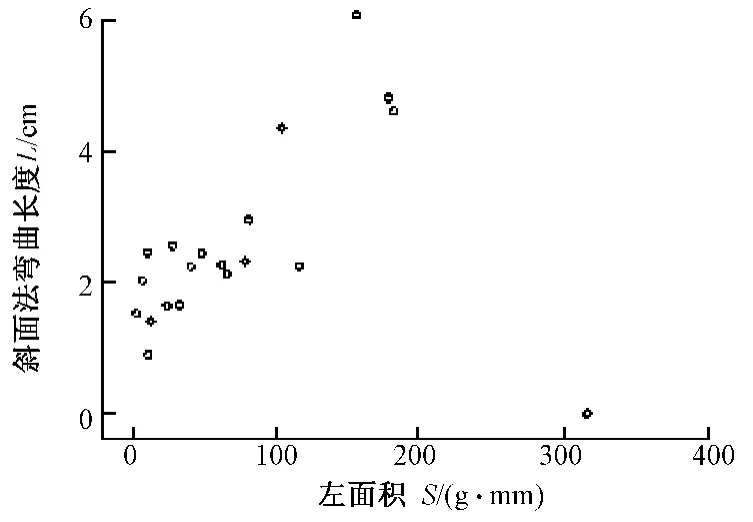
图6 CHES-FY的左面积S与斜面法弯曲长度的线性回归分析Fig.6 Linear regression analysis of left area S and bending length of Cantilever test

CHES-FY系统测试曲线特征值中的左斜率k、峰值Y和左面积S与织物弯曲性能相关，利用SPSS软件将CHES-FY系统测试中的3个相关特征值与斜面法测得弯曲长度作多元线性回归分析，可更优地表征织物的弯曲性能。

采用SPSS相关性分析中的进入法对提取特征指标:左斜率k、峰值Y和左面积S(自变量)与斜面法测试时的弯曲长度(因变量)进行多元线性回归分析。由于采用进入法，没有剔除变量，保留了全部3个变量，其多元回归结果如表3所示。

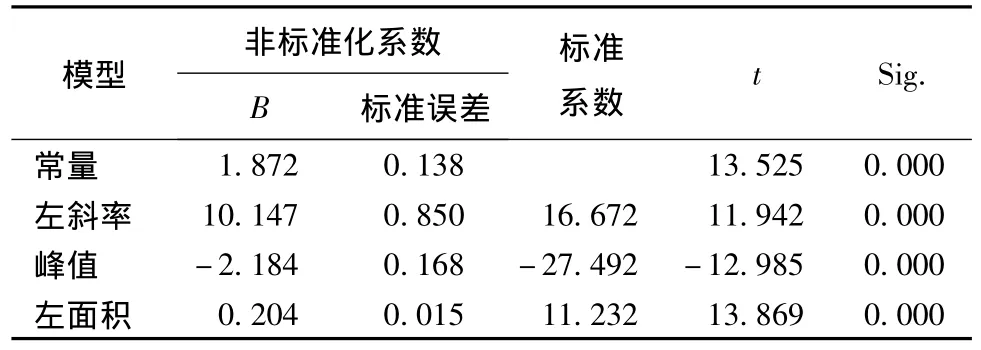
表3 回归方程中的回归系数(斜面法)Tab.3 Regression coefficient of regression equation(cantilever test)

多元线性回归系数R为0.926，说明回归方程建立的比较好，所以回归方程可满足线性与方差齐性的假设且拟合效果好。方差分析结果表明，当回归方程包含3个不同自变量时，其显著性概率小于0.001，即拒绝总体归回系数为0的假设，因此，最终方程应包含着3个变量。

由表3中回归结果分析得出其多元线性回归方程为L=1.872+10.147k－2.184Y+0.204S。

2.3 CHES-FY系统测试与心形法相关性

为了分析CHES-FY系统测试实验过程中提取的曲线特征值(左斜率k、峰值Y和左面积S)与心形法测得的弯曲长度的关系，首先分别作每个变量与心形法的弯曲长度的线性回归分析，结果如图7～9所示。可以看出，3个变量与织物心形法的弯曲长度之间有较好的线性关系，CHES-FY系统的左斜率k、峰值Y和左面积S与心形法的弯曲长度的相关系数分别为 0.646、0.642、0.648，说明用 CHES-FY系统与心形法测试的弯曲长度具有很好的相关性，CHES-FY系统能较为准确地测量织物的弯曲性能。

图7 CHES-FY系统测试的左斜率k与心形法弯曲长度的线性回归分析Fig.7 Linear regression analysis of left slope k and bending length of Heart Loop test

对于CHES-FY系统测试曲线特征值中的左斜率k、峰值Y和左面积S，采用SPSS软件分析与心形法测得弯曲长度的多元线性回归关系，采用SPSS相关性分析中的进入法分析左斜率k、峰值Y和左面积S(自变量)与心形法测试时的弯曲长度进行多元线性回归分析，结果如表4所示。

由表4可知，多元线性回归系数R为0.838，说明回归方程建立的比较好。方差分析结果表明，当回归方程包含3个不同自变量时，其显著性概率小于0.001，即拒绝总体归回系数为0的假设，因此，最终方程应包含3个变量，其方程拟合效果较好。

图8 CHES-FY系统测试的峰值Y与心形法弯曲度的线性回归分析Fig.8 Linear regression analysis of peak Y and bending length of Heart Loop test

图9 CHES-FY系统测试的左面积S与心形法弯曲长度的线性回归分析Fig.9 Linear regression analysis of left area S and bending length of Heart Loop test

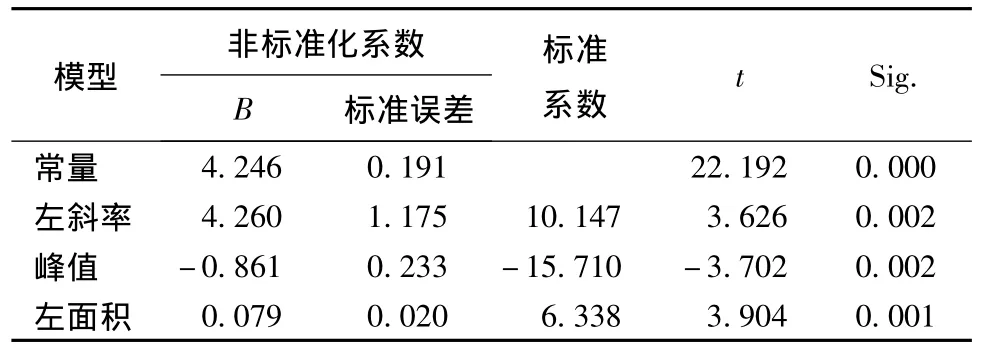
表4 回归方程中的回归系数(心形法)Tab.4 Regression coefficient of regression equation(heart loop test)

表4为回归结果分析表，其多元线性回归方程为L=4.246+4.26k－0.861Y+0.079S。

2.4 仪器特征值的分辨率和重现性

在分析了CHES-FY系统测试特征值与斜面法、心形法测试结果的相关性之后，为了进一步确定CHES-FY系统测试是否能有效地表征织物弯曲性能，对当前条件下的测试结果进行了灵敏度(对不同硬挺度织物的区分和硬挺测试数据的范围作为本次测量的灵敏度)和重现性分析。

2.4.1 CHES-FY系统测试特征值的灵敏度

为了定量表征CHES-FY系统测试的优越性，采用左斜率、峰值和左面积的灵敏度［9］作为评价指标，对20组CHES-FY系统测试的曲线特征值和斜面法、心形法的弯曲长度进行灵敏度分析，结果如表5所示。

表5 CHES-FY系统测试和斜面法、心形法灵敏度分析Tab.5 Sensitivity analysis of CHES-FY system test，Cantilever test and Heart Loop test

由表5知，CHES-FY系统测试的曲线3个特征值的 CV值和极差分别是 1.15、2.93，1.09、2.71，1.03、2.11，而斜面法和心形法的CV值和极差分别为 0.23、0.62;0.2、－0.19，CHES-FY 系统特征值的CV值和极差比斜面法和心形法的测试值的CV值和极差都高，说明CHES-FY系统能更好地区分不同硬挺度的织物及更广泛的测试数据范围，表明CHES-FY系统有更高的灵敏度，能区分明显差异的柔软和硬挺织物，也能区分硬挺度较为接近的织物。

斜面法测试弯曲长度中1号试样无法进行测量，心形法测试结果非常接近，表明难以区分硬挺接近的织物试样;而CHES-FY系统不仅定量测试了其弯曲性能，而且能较大地区分硬挺度接近的织物，表明其测试灵敏度高，测试试样的适用性更广。

2.4.2 3台仪器测试的重现性

在相同实验条件下，用CHES-FY系统对20种试样进行了3次重复测试，在测试曲线中分别提取左斜率、峰值和左面积，并根据已经分析出来的斜面法弯曲长度与3个指标的方程关系:L=1.872+10.147k－2.184Y+0.204S，将3个指标带入方程，得到理论弯曲长度值;然后，计算试样3次重复测时所得的弯曲长度的CV值;同时计算斜面法和心形法的弯曲长度的CV值，其结果见表6。

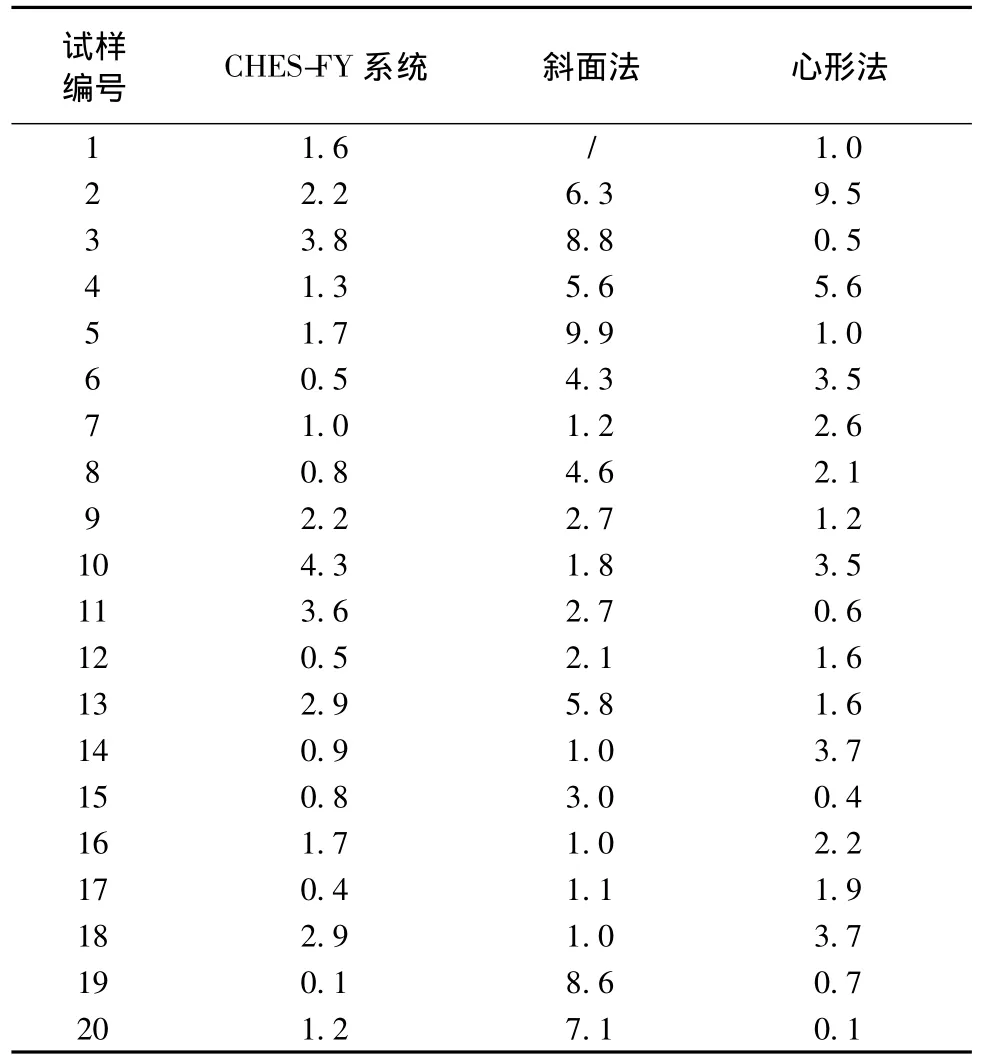
表6 20组试样的CV值Tab.6 CV of 20groups of sample

从表6可以看出，所测织物试样的弯曲长度的CV值全部小于5%，说明在本文实验参数组合下，CHES-FY、斜面法和心形法的测试结果稳定，重复性好，可有效地用于测试试样的弯曲性能。

基于CHES-FY系统测试的弯曲阶段的特征值较为稳定，并能高灵敏度地鉴别硬挺度接近的织物和宽范围的适用性，表明仪器在测试非织造、复合材料、针织、机织等织物弯曲性能的稳定性较好，可以比较稳定、真实地反映织物的弯曲性能。

3 结论

本文在相同实验条件下采用CHES-FY系统对20组织物试样(包含非织造布、复合材料、针织物、机织物)进行了测试，从抽拔力-位移曲线上提取左斜率、峰值和左面积3个特征值;采用SPSS对3个特征值与斜面法、心形法的弯曲长度进行了相关性分析，结果表明相关性较好。同时，对CHES-FY系统的灵敏度和实验重现性进行了分析，其灵敏度远高于斜面法和心形法测试弯曲性能，实验重现性稳定。CHES-FY系统能较为准确清晰地反映织物的弯曲性能，并且有很好的灵敏度和实验重现性，因此，能客观准确地表达织物的硬挺性能。

［1］PARK J W，OH A G.Bending rigidity of yarns［J］.Textile Research Journal，2006，76(6):478 －485.

［2］VASSILIADIS S，KALLIVRETAKI A，DOMVOGLOU D，et al.Mechanical analysis of woven fabrics:the state of the art［J］.Advances in Modern Woven Fabrics Technology，2011，27(7):41 －64.

［3］KANG T J，JOO K H，LEE K W.Analyzing fabric buckling based on nonlinear bending properties［J］.Textile Research Journal，2004，74(2):172 －177.

［4］ABBOTT N J.The measurement of stiffness in textile fabrics［J］.Textile Research Journal，1951，21(6):435－441.

［5］PAN N，YEN K C.Physical interpretations of curves obtained through the fabric extraction process for handle measurement［J］.Textile Research Journal，1992，62(5):279－290.

［6］PAN N.Quantification and evaluation of human tactile sense towards fabrics［J］.International Journal of Design and Nature，2007，1(1):48－60.

［7］MINAZIO P G.FAST-fabric assurance by simple testing［J］.International Journal of Clothing Science and Technology，1995，7(2/3):43－48.

［8］DU Z Q，ZHOU T，YAN N，et al.Measurement and characterization of bending stiffness for fabrics［J］.Fibers and Polymers，2011，12(1):104 －110.

［9］SUN C，GAO R，DU Z，et al.Determination of optimal system parameters to measure bending property of fabric based on the CHES-FY system［J］.Fibers and Polymers，2014，15(4):874 －881.

［10］DU Z，GAO R，ZHOU T，et al.Effects of parameters on mass index of the CHES-FY system［J］.Fibers and Polymers，2014，15(1):175 －180.