350 MW级蓄能机组可倾瓦导轴承流体动力润滑计算

范寿孝,全日光,朱亲林

(哈尔滨电机厂有限责任公司, 哈尔滨 150040)

350 MW级蓄能机组可倾瓦导轴承流体动力润滑计算

范寿孝,全日光,朱亲林

(哈尔滨电机厂有限责任公司, 哈尔滨 150040)

为了解决大型抽水蓄能机组可倾瓦导轴承性能计算的问题,笔者根据流体润滑理论,建立了大型可倾瓦导轴承的流体动力润滑数学模型,设计了计算程序,并以此程序对某350 MW级抽水蓄能机组的导轴承润滑性能进行了计算分析和研究。其结果表明,大型可倾瓦导轴承的流体动力润滑计算程序运行稳定可靠,导轴承的动力润滑性能会受到轴承负荷、机组转速、油槽进油温度等因素的影响,最高油膜温度、最小油膜厚度是制约轴承运行工况参数变化范围的关键因素。

350 WM级;抽水蓄能机组;可倾瓦导轴承; 流体动力润滑

目前,抽水蓄能电站起到了优化电源结构、实现电力系统节能减排和资源节约利用的作用[1]。大型抽水蓄能机组的导轴承主要承受机组转动部分的机械径向不平衡力和电磁不平衡力,使机组轴系的临界转速和摆度满足相关标准要求。若轴承设计不当,则会增加轴承系统的损耗,降低机组效率,甚至影响机组的安全运行和使用寿命。随着循环泵、抽水蓄能机组等向着高速、大容量发展[2-3],对可倾瓦导轴承的润滑性能提出了更高要求。因此,本文针对350 MW级抽水蓄能机组可倾瓦导轴承动力润滑计算的问题,通过分析其结构特点并依据流体润滑理论,建立了大型可倾瓦导轴承的流体动力润滑模型,并开发了计算程序,对某350 MW级抽水蓄能机组的导轴承动力润滑性能进行计算分析和研究。

1 导轴承计算模型及程序建立

抽水蓄能机组的可倾瓦导轴承由若干块导瓦组成,导瓦的支撑点为导瓦中心处,通过支撑结构固定在机架上,从而满足机组的双向运行要求。对于一般的抽水蓄能机组,上导轴承为单独油槽,下导轴承与推力轴承共用油槽。

油膜的压力、温度、厚度以及轴承损耗等参数充分体现了可倾瓦导轴承性能的优劣。而这些性能参数与转速、负荷、进油温度、润滑油粘度、轴承的结构尺寸等密切相关。只有联立润滑油膜的动压方程(Reynolds方程)、热能量方程、油膜厚度公式、润滑油温度——粘度公式等组成的方程组才可以准确的描述轴承润滑的过程,通过联立相关方程并进行迭代求解,可计算出导轴承的润滑性能参数[4-7]。

1) Reynolds方程为

(1)

边界条件:沿瓦面周边压力为0。

2) 能量方程为

(2)

边界条件:入油边为润滑油温度,上下端面为绝热边界。

3) 油膜厚度方程为

hi=c-(c-c′)cos(βi-φi)+ecos(φi-θ)+rδisin(βi-φi)

(3)

4) 润滑油温度与粘度关系为

μ=μ0×f(T,T0)

(4)

式中:P为油膜压力;T为油膜温度;x,z为坐标;h为油膜厚度;B为轴承宽度;r为轴颈半径;c为轴承间隙;c′为装配间隙;δ为预负荷系数;μ为润滑油粘度;cν为润滑油比热容;θ为偏位角;ρ为润滑油密度;u为线速度;β为各瓦的支点位置角;φi为计算点位置角;μ0为参考点润滑油粘度。可倾瓦导轴承流体动力润滑计算程序流程如图1所示。根据计算流程,编制开发了计算程序。

2 导轴承动力润滑计算结果分析

本文以某抽水蓄能机组下导轴承为例进行计算,参数如表1所示。

2.1 进油温度对轴承性能的影响

当轴承负荷36 kN、机组转速400 r/min不变时,轴承进油温度由30 ℃变化到50 ℃,轴承润滑性能参数的变化如图2～5所示。

从图2～5可以看到,随着进油温度的升高,最小油膜厚度由58 μm减小到48.7 μm;最高油膜温度由85.6 ℃升高至96.3 ℃;轴承损耗由301.6 kW下降到250 kW;油膜压力有一定波动,波动范围在0.12 MPa范围内;最小油膜厚度、最高油膜温度是限制轴承进油温度变化的主要因素。而随着进油温度的升高,润滑油温度也会升高,致使参与润滑的油液粘度降低,从而减小油膜厚度,降低油膜损耗。

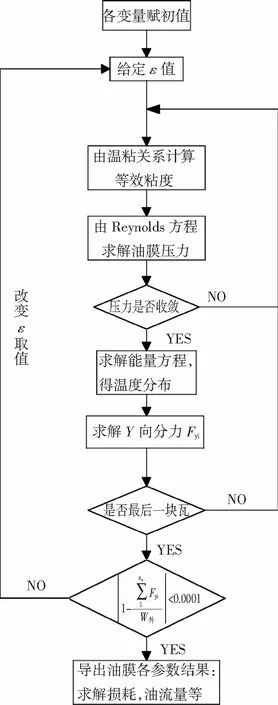
图1 计算程序流程图

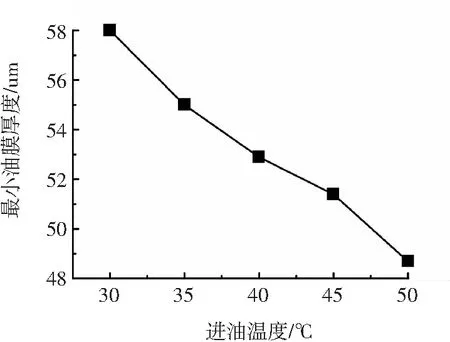
图2 最小油膜厚度随进油温度变化

Fig.2 The minimum oil film thickness varies with inlet oil temperature

表1 某蓄能机组下导轴承设计参数

图3 最高油膜温度随进油温度变化

Fig.3 The maximum oil film temperature varies with inlet oil temperature

图4 最大油膜压力随进油温度变化

Fig.4 The maximum oil film pressure changes with inlet oil temperature

图5 轴承损耗随进油温度变化

Fig.5 Change of bearing loss with inlet oil temperature

2.2 转速变化对轴承性能的影响

当轴承负荷36 kN、进油温度40 ℃不变时,不同转速工况下导轴承润滑性能如表2所示。

由表2可以看出,随着转速由200 r/min增至600 r/min,最小油膜厚度增加了6.4 μm;最大油膜压力变化不明显,其主要原因是转速增大会引起润滑油剪切力增大,但同时油膜厚度的增大会导致油膜压力下降,两者综合作用最终致使最大油膜压力基本不变。

第四，“互联网+养老”模式有助于丰富养老服务的内容和产品种类，提高老年人的生活质量，实现老有所养，老有所医，老有所乐，老有所享。在人口老龄化的带动下，我国老年人的养老需求也在日趋多样化，从过去单纯的生存需求逐步扩展到医疗保健、精神慰藉、社会交往等方面。“互联网+”利用大数据和网络传播等技术能提供服务平台，与医疗、旅游、交通、网络交流等紧密联系在一起，可以为老年人提供内容更为丰富、种类更为多样的养老服务。这将大大提高老年人的生活质量，减轻家庭中年轻一代的养老负担。更可以成为银发经济产业，扩大内容，成为可持续的经济增长突破口。

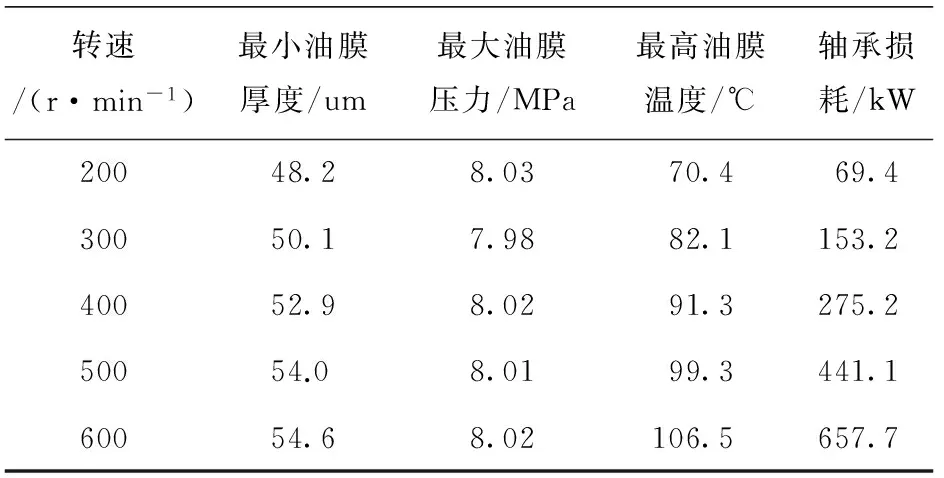
表2 转速变化对轴承性能的影响

由于转速增大直接影响到了轴承损耗和最高油膜温度,轴承损耗由70 kW上升至650 kW,最大油膜温度由70.4 ℃升高至106.5 ℃,增加了旋转部件的搅拌损耗,增大了油膜温度。因此,最高油膜温度和轴承损耗是限制转速变化的关键因素,在设计轴承润滑冷却系统时,必须考虑飞逸工况下轴承损耗增大的影响,以保障润滑冷却系统具有足够的余量,确保轴承各工况下安全运行。

2.3 轴承负荷变化对轴承性能的影响

当转速600 r/min、进油温度40 ℃不变时,不同轴承负荷工况下导轴承润滑性能如表3所示。

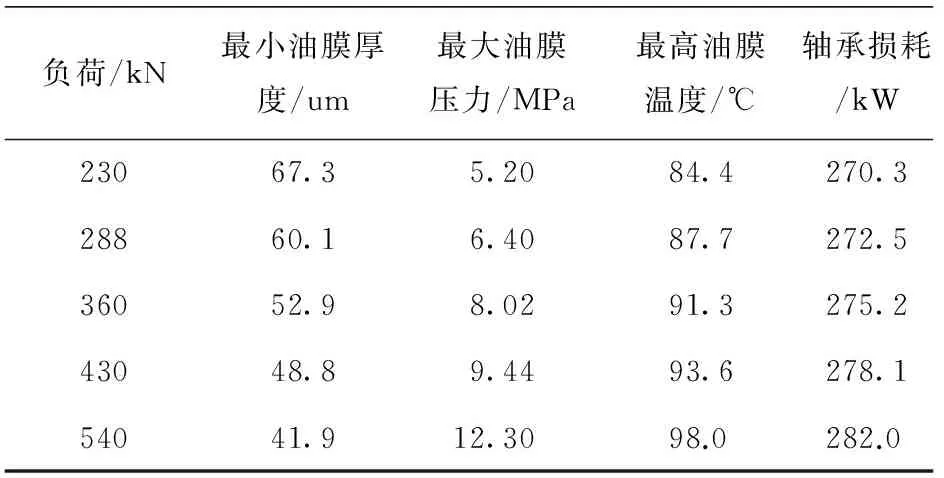
表3 负荷变化对轴承性能的影响

由表3可以看出,随着轴承负荷的增加,最小油膜厚度由67.3 μm迅速下降至41.9 μm,最大油膜压力由5.2 MPa升至12.5 MPa,最高油膜温度由84.4 ℃升至98 ℃,但轴承损耗变化不明显。由此可以看出,轴承损耗与负荷的关系不大。由于最小油膜厚度和最高油膜温度为轴承润滑性能的重要指标,因此它也成了限制轴承负荷增大的因素。

3 结 论

通过利用流体动力润滑理论对350 MW蓄能机组可倾瓦导轴承的润滑性能进行计算分析与研究,得到了以下结论:

1) 350 MW蓄能机组可倾瓦导轴承的润滑计算程序运行稳定、可靠。

2) 进油温度的升高会导致导轴承的最小油膜度和轴承损耗减小,使最高油膜温度升高。

3) 转速变化对轴承润滑性能有一定的影响,轴承损耗随着转速的增加呈倍数级增加。

4) 随着轴承负荷的增加,最高油膜温度增大,最小油膜厚度减小,从而成为制约轴承承载力的关键因素。

[1] 曹明良.抽水蓄能电站在我国电力工业发展中的重要作用[J].水电能源科学,2009,27 (2):212-214. CAO Mingliang. Important role of pumped storage power station in power system development of China [J]. Water Resources and Power, 2009,27 (2):212-214.

[2] 田树棠. 大型抽水蓄能机组发展动向与比转速选择[J]. 陕西水力发电,1995(4):46-52. TIAN Shutang. Development trend of large-scale pumped storage unit and selection of specific speed [J]. Journal of Shanxi Water Power, 1995(4):46-52.

[3] 戴庆忠. 日本抽水蓄能机组技术发展近况[J]. 东方电机,2008(1):9-29. DAI Qingzhong. Recent development of pumped-storage units in Japan [J]. Oriental, 2008(1):9-29.

[4] 孟繁娟. 径向滑动轴承油膜压力分析[J]. 轴承,2008(1):25-32. MENG Fanjuan. Analysis of film pressure of radial sliding beari-ng [J]. Bearing, 2008(1):25-32.

[5] 马希直. 导轴承性能热流体动力分析[J]. 润滑与密封,2000(3):12-14. MA Xizhi. Thermohydrodynamic analysis of properties of guide bearing [J]. Lubrication Engineering, 2000(3):12-14.

[6] 张直明. 滑动轴承的流体动力润滑理论[M].北京:高等教育出版社, 1986. ZHANG Zhiming. Theory of hydrodynamic lubrication of sliding bearing [M]. Beijing: Higher Education Press, 1986.

[7] 吕延军,虞 烈,刘 恒. 基于Reynolds边界的滑动轴承动力学系数的计算及应用[J]. 摩擦学学报,2004,24(1):61-65. LV Yanjun, YU Lie, LIU Heng. Calculation of dynamic coefficients of a journal bearing based on Reynolds boundary and its application [J]. Tribology, 2004,24(1):61-65.

(责任编辑 侯世春)

Calculation of hydrodynamic lubrication of tilting pad guide bearing for 350 MW pumped-storage units

FAN Shouxiao, QUAN Riguang, ZHU Qinlin

(Harbin Electrical Machinery, Harbin 150040,China)

In order to solve the calculation problem of the tilting pad guide bearing for large pumped-storage units, according to hydro lubricating theory, the author established the hydrodynamic lubricating mathematical model of the tilting pad guide bearing and analyzed and studies the hydrodynamic lubrication of a 350 MW pumped-storage unit by the designed calculation program. The result shows that the calculation program operates stably and reliably. Besides, the lubricating character of guide bearing is affected by factors including bearing load, unit speed and inlet oil temperature of oil tank. The maximum oil film temperature and the minimum oil film thickness become the critical factor restricting the variation range of operating parameters.

350 WM; pumped-storage unit; tilting pad guide bearing; hydrodynamic lubrication

2015-03-17。

范寿孝(1984—),男,工程师,硕士,研究方向为大型发电机轴承技术研究与设计。

TM303 TH133.3

A

2095-6843(2015)05-0433-03