基于动态NW小世界量子粒子群算法的电力系统无功规划优化

陈志江, 彭祖群，陈育成

(广东工业大学 自动化学院 广州 510006)

●学术研究●

基于动态NW小世界量子粒子群算法的电力系统无功规划优化

陈志江, 彭祖群，陈育成

(广东工业大学 自动化学院 广州 510006)

为了解决电力系统无功规划优化问题，提出一种动态NW小世界量子粒子群算法(NWQPSO)，改善了传统量子粒子群算法易陷入局部最优的缺点。将NW小世界的动态拓扑结构应用到粒子进化公式中，增加了迭代过程中粒子多样性，使其多局部搜索和全局性搜索。利用电压稳定裕度指标，寻找系统电压稳定性较薄弱节点，将其作为无功补偿安装点，以无功补偿装置投资和网损综合费用为目标函数，通过IEEE30节点系统的仿真，验证了该规划方法和算法的有效性。

无功规划优化；静态电压稳定裕度指标；NW小世界；量子粒子群

无功规划优化是一个多变量、多约束的混合非线性规划问题，是保持电力系统无功平衡、降低网损并保证电力系统安全运行的重要措施，是电力系统规划的重要组成部分。求解方法主要有数学规划法和各种智能算法，其中包括遗传算法(GA)、粒子群算法(PSO)、量子粒子群算法(QPSO)。GA、PSO的初始值选取不当和进化方式规范化容易出现陷入局部最优解的问题, 而QPSO可使粒子在整个可行解空间中搜索寻求全局最优解，使算法在收敛性能上得到一定程度的提高[1]。然而由于其以概率收敛的进化方式，导致粒子不可避免地丢失多样性，使得后期收敛速度变慢，同时算法收敛到一定精度时无法继续优化，进而陷入局部最优解。因此针对这个问题有学者提出了诸多解决方法，如带极值扰动的QPSO算法[2]、采用混沌序列初始化量子的初始角位置的混沌QPSO算法[3]、带自适应变异算子的AMQPSO算法[4]、协同量子粒子群ICQPSO算法[5]等改进方法。文献[6]利用柯西分布比较高的两翼概率的特性使QPSO能更快跳出局部最优值法。文献[7]用Sobol序列对平均最好位置进行随机扰动，增加迭代过程中粒子多样性。文献[8-9]将环形拓扑结构和小世界网络引入PSO，获得更好的搜索能力法。基于此，本文在总结上述方法优缺点的基础上，提出一种基于动态NW小世界网络的量子粒子群算法(Dynamic NW Samall World Quantum particle Swarm Algorithm, NWQPSO)，利用电压稳定裕度指标Ivs[10]寻找系统薄弱的负荷节点，将这些节点作为无功规划节点，把NW小世界网络引入QPSO算法中，利用此算法寻找各待规划节点的无功规划容量，并通过对电力系统IEEE30节点的仿真计算，验证了该算法在无功规划优化问题的良好效果。

1 无功规划数学模型

1.1 电压稳定裕度指标

文献[10]从某一负荷节点出发将系统等效为戴维南等效模型，并将系统阻抗模值与该负荷等效阻抗模值之比定义为电压稳定裕度指标。当这一比值大于某一标准值时，系统电压将可能出现不稳定。以负荷节点i为例，其计算方法如下:

1) 输入线路和节点数据，形成节点导纳矩阵，求逆获得节点阻抗矩阵，其对角线元素Zbus.i.i即为该节点i的戴维南等效阻抗。

2) 用潮流计算得到节点i的电压Vi，通过下式得到节点i的阻抗值：

Zload.i=Vi2/Si

式中，Si、Vi为节点i的复功率和电压幅值。

3) 计算电压稳定裕度指标Ivs：

1.2 目标函数

以无功补偿装置投资和网损综合费用为目标函数，追寻目标函数的最小值。

式中：c1为电价，元/kWh；c2为无功补偿设备每年折合投资单价，万元/MVA；Pagoloss为进行无功规划前的有功网损， MW；Pnowloss为无功规划后的有功网损, MW；Qi为节点i处电容器总补偿容量， MVA；M为补偿点的集合；f1为由于网损引起的运行费用，万元；f2为由于网损和无功补偿装置装设引起的费用，万元；tmax为最大负荷损耗小时数；F为目标函数值。

1.3 约束条件

1) 潮流方程约束为：

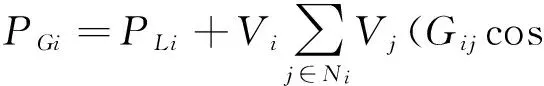
式中：PGi、PLi分别为节点i的有功注入和有功负荷；QGi、QCi、QLi分别为节点i的无功注入、无功补偿容量及无功负荷;Gji、Bij、θij分别为节点i、j之间的电导、电纳及电压相角差。

2) 状态变量的不等式约束为：

Vimin≤Vi≤Vimax

QGjmin≤QGj≤QGjmax

式中：Vimin，Vimax分别表示节点电压上下限；QGjmin，QGjmax分别为发电机无功输出功率上下限。

3) 控制变量的不等式约束为：

VGjmin≤VGj≤VGjmax

QCi≤QCimax

Timin≤T≤Timax

式中：VGjmin，VGjmax分别为PV节点电压上下限；QCimax为第i个待选补偿节点所允许安装电容器组的容量上限；Timin，Timax为分别为第i个变压器变比上下限。

2 基本量子粒子群算法(QPSO)

文献[1]以DELTA势阱为基础，认为粒子具有量子的行为，提出了量子粒子群算法。在量子空间中，不能同时确定粒子速度和位置。通过波函数来描述，并以求解薛定谔方程的方式得到粒子出现在空间某点的概率密度函数。随后通过蒙特卡罗(Monte Carlo)模拟的方式得到粒子的位置方程为

式中：u为[0,1]上的均匀分布随机数，L(t+1)=2β|mbest-X(t)|。

最后得到QPSO算法的进化方程为:

(1)

式中：M为种群中粒子数目；D为粒子维数；φ为[0,1]上服从均匀分布的量子粒子学习因子；mbest(t)为第t次迭代的种群中全部粒子平均最佳位置；Pi(t)，Pg(t)，Pid(t) 分别为第t次迭代时第i个粒子的当前最佳位置(pbest)、全局最优位置(gbest)和两个最优位置之间的随机点。β为收缩扩张系数，其计算表达式为一般按照下式取值：

β=m-(m-n)×t/MaxTimes

(2)

式中： 随着迭代线性地从m递减到n，通常取m=0.9,n=0.5；MaxTimes为最大迭代次数。

3 基于动态NW小世界的量子粒子群算法(NWQPSO)

3.1 动态NW小世界网络拓扑结构

动态NW 小世界网络模型：首先构造一个含有N个节点的最近邻耦合网络,其中每个节点都与它左右相邻的各k/2个节点相连而围成环,k是偶数,即节点的度；然后以概率P随机选取一对节点之间加上一条边，其中任意两个不同节点之间最多一条边, 并且节点与自身不能相连。

根据文献[11]用matlab软件平台构造NW小世界网络模型，网络的连接用邻接矩阵anxn表示，其中n表示网络的节点数(在本文中表示粒子数)。aij=1表示节点i(在本文中表示粒子i)和节点j(在本文中表示粒子j)有边连接；aij=0 表示节点i和节点j无边相连。产生随机加边概率P的方法和随机选择节点编号的方法是利用均匀随机数产生器产生连续的及离散的随机数来代替。为了增加信息的流通渠道，随机加边概率P随着算法迭代次数的改变而变大，更新公式如下：

(3)

式中：t为第t次迭代,maxtimes表示最大迭代次数，P为随机概率。

3.2 NWQPSO算法的Pid(t+1)更新方式

在基本量子粒子群中，Pid(t+1) 使用第t代的第i个粒子的pbest和gbest更新位置信息，是一种全连接的拓扑结构。信息传播的单一性使得收敛过程迅速，逐渐丢失多样性，并容易陷入局部最优。这是因为一旦当前全局最优信息为局部最优值时，其余粒子受其牵引，并且以概率收敛的进化方式的粒子丢失了多样性，迅速陷入局部最优位置，造成算法的早熟收敛。为此，使用NW小世界网络的动态拓扑结构来改造Pid(t+1) 的更新方式，增加粒子进化的多样性，改善量子粒子群的收敛性能。

在NWQPSO算法中，Pid(t+1) 使用的是NW小世界网络的动态拓扑结构，所以粒子仅使用自身和邻域中所包含的信息进行更新，更新方式为

(4)

式中：r1、r2为[0,1]上的随机数；c1、c2为权重系数，可调整Pid(t+1) 偏向个体还是领域信息，本文中保守设置c1、c2都为1.5，避免因分母太小而出现错误；Plgd(t) 为在第t次迭代时与第i个粒子有连接的粒子中适应度最好的粒子lgbest，此种粒子连接方式改变了信息更新方向。

在第t次迭代中NW小世界动态拓扑结构中的粒子，每个粒子的邻域均唯一，其Pid(t+1) 信息更新方式由邻域内的局部最优位置和个体历史最优位置决定。每个粒子使用其邻域内的信息，为整个粒子群拓扑内所包含的一小部分信息，而每个粒子所使用的邻域信息均不一样，增加了粒子的多样性，进而得到更好的优化效果。

4 无功规划优化步骤

1) 输入原始数据，输出潮流计算结果，根据潮流结果计算系统各个负荷节点的电压稳定裕度指标Ivs, 并按照从大到小排序。

2) 选择Ivs指标较大(即静态电压稳定裕度较小)的前m个节点或大于某一定值的节点作为无功补偿规划点。

3) 生成初始种群，并计算每个粒子的适应度值，生成pbest、gbest。

4) 生成NW小世界网络拓扑结构，随机加边概率P由式 (3) 决定，生成并更新lgbest。

5) 由式 (1)、(2)、(4) 来更新粒子的速度与位置。注意式 (1) 中的Pid(t+1) 由式 (4) 代替。优胜劣汰更新 pbest、gbest。

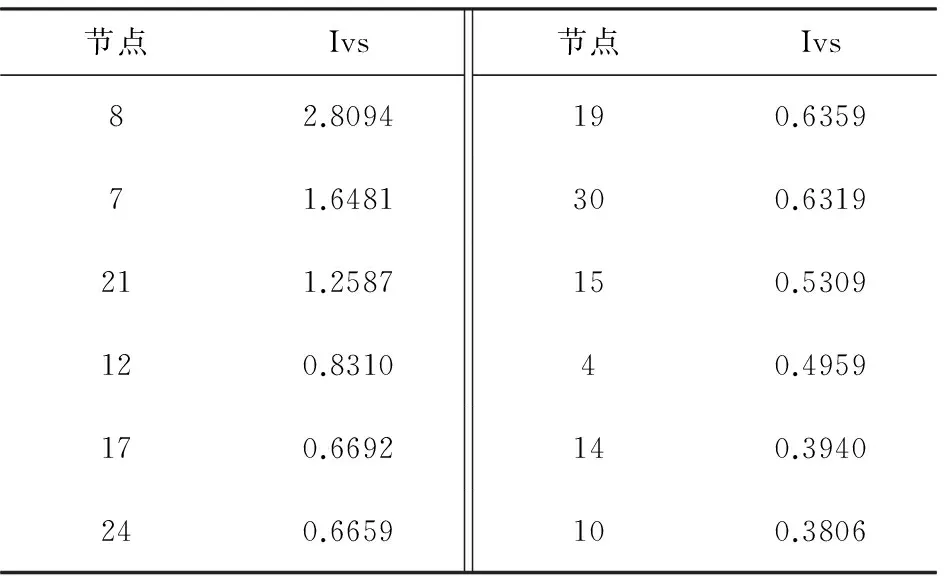
6) 判断停止准则，如果迭代次数t

7) 输出各待规划节点的无功装置规划容量，算法停止。

5 算例分析

5.1 规划效果分析

将本文提出的规划方法运用于matlab matpower文件包的 IEEE30节点系统，6台发电机，20个负荷节点，电压设置为0.97～1.07。每个节点最大规划电容量为 50 MVA。参数tmax设置为8760 h,电价c1为0.5元/kWh；c2为0.3万元/MVA。

计算了该IEEE30节点系统中各个负荷节点的静态电压稳定裕度指标Ivs，并列举了12个负荷点的Ivs值，并按从大到小排序，如表1所示。

负荷节点的Ivs指标值越大，表示该节点的电压稳定性越差。为留有一定的裕度，选择表1中大于0.5的9个点作为无功规划补偿点，应用NWQPSO算法对IEEE30节点系统进行了无功规划计算，NWQPSO参数设置为种群大小100，迭代次数150，NW小世界网络k=6。规划结果如表2所示。

表1 负荷节点的Ivs指标

表2 IEEE30节点系统的变量控制范围和规划结果

通过无功规划后发电机的无功出力在允许范围内，所有节点的电压合格，网损从2.444 MW降到1.8239 MW，降幅达25.37%，运行综合费用从1070.5万元降到819万元，降幅达23.49%，系统运行更加经济。并且所选中的规划节点的Ivs指标都有大幅度减小，提高了系统的电压稳定性，具体结果如表3所示。

5.2 算法对比分析

采用QPSO和NWQPSO算法对IEEE30节点系统进行无功规划优化仿真，规划模型如上设置，算法测试参数设置如下：

表3 规划节点的Ivs指标对比

1) QPSO参数设置为种群大小100，迭代次数150；

2) QPSO参数设置为种群大小100，迭代次数300；

3) NWQPSO参数设置为种群大小100，迭代次数150，k=6；

4) NWQPSO参数设置为种群大小100，迭代次数300，k=6。

为避免偶然误差,各算法均独立运行30次，统计结果如表4所示。取QPSO和NWQPSO算法的最优结果得出的收敛特性曲线如图5所示。

表4 算法性能比较

图5 收敛特性曲线

从图5可看出，QPSO迭代到75代左右已收敛，而NWQPSO则在110代还具有较强搜索能力并且向最优值又迈进了一步，这正是NW小世界动态拓扑结构运用于该算法使粒子信息传输多向性的作用。从表4可看出， NWQPSO的稳定性也比QPSO好：在迭代150次时，NWQPSO适应度值一直稳定在0.766左右，而QPSO稳定在0.767左右并经常陷入局部最优0.78左右的值；在迭代300次时，两种算法最优值精度都有提高，但平均值QPSO远远大于NWQPSO，且QPSO的平均值与最优值的差值甚大，随着迭代次数的增加QPSO依然陷入局部最优0.7817，而NWQPSO的最差值已接近于平均值。这又充分证明了NWQPSO算法强大的搜索能力。

5 结 语

运用电压稳定裕度指标Ivs，寻找系统电压稳定性较薄弱节点，并选其为无功补偿装置安装点，以无功补偿装置投资和网损综合费用为目标函数，采用基于动态NW小世界网络的量子粒子群算法对无功规划问题进行求解。通过对IEEE30节点系统的仿真验证了该方法的有效性，而且NWQPSO不易陷入局部最优，算法的搜索能力比QPSO更强。

[1] SUN J，FENG B，XU W B．Particle Swarm Optimization with Particles Having Quantum Behavior[C]//Proceedings of 2004 Congress on Evolutionary Computation.2004:325-331．

[2] 阳成虎，杜文．基于改进QPSO算法的逢低买入最优定价研究[J]．计算机工程与应用，2008(8)：210-211． YANG Chenghu, DU Wen. Optimal pricing with group-buying auction based on modified QPSO [J]. Computer Engineering and Applications, 2008(8)：210-211．

[3] 黄宇,韩璞,刘长良,等. 改进量子粒子群算法及其在系统辨识中的应用[J]. 中国电机工程学报,2011,31(20):114-120.HUANG Yu, HAN Pu, LIU Changliang, et al. An improved quantum particle swarm optimization and its application in system identification [J]. Proceedings of the CSEE, 2011,31(20):114-120.

[4] 葛洪伟，靳文辉．变异量子粒子群优化算法在系统辨识中的应用[J].计算机工程与应用，2007，43(29)：222-224． GE Hongwei, JIN Wenhui. Application of quantum-behaved PSO algorithm with mutation operator in system parameters identification [J]. Computer Engineering and Applications, 2007，43(29)：222-224．

[5] 相荣荣. 协同量子粒子群优化及其应用研究[D].西安：西安电子科技大学,2012. XIANG Rongrong. Cooperative quantum particle swarm optimization and its application [D]. Xi’an: Xidian University, 2012.

[6] 余许磊. 基于量子粒子群算法的电力系统经济调度仿真研究[D].西安：西安科技大学,2013. YU Xulei. A simulation study on economic dispatch of electrical power system based on the quantum-behaved particle swarm optimization [D]. Xi’an: Xi’an University of Science and Technology, 2013.

[7] 张兰. 基于Sobol扰动的量子粒子群算法的电力经济调度[J]. 计算机与现代化,2013(9):195-198. ZHANG Lan. Power economic dispatch of quantum-behaved particle swarm optimization based on school disturbance [J]. Computer and Modernization , 2013(9):195-198.

[8] 何占琦,孟安波,陈育成,等. 基于环形拓扑的粒子群优化算法在无功优化中的应用[J]. 广东电力,2014,32(2):56-59. HE Zhanqi, MENG Anbo, CHEN Yucheng, et al. Application of particle swarm optimization algorithm based on ring topology in reactive power optimization [J]. Guangdong Electric Power, 2014,32(2):56-59.

[9] 唐京瑞,毕贵红,王曦. 基于小世界网络的PSO算法在电力系统中的应用[J]. 中北大学学报：自然科学版,2012,32(2):135-140. TANG Jingrui, BI Guihong, WANG Xi. Application of small world network PSO algorithm in power system [J]. Journal of North University of China (Natural Science Edition), 2012,32(2):135-140.

[10] MANJURE D P, MAKRA E B. Steady state stability assessment using the bus impedance matrix[C]//2001 Large Engineering Systems Conference on Power Engineering. 2001: 153-157.

[11] 王波,王万良,杨旭华. WS与NW两种小世界网络模型的建模及仿真研究[J]. 浙江工业大学学报,2009,37(2):179-182. WANG Bo, WANG Wanliang, YANG Xuhua. Research of modeling and simulation on WS and NW small-world network mod-el [J]. Journal of Zhejiang University of Technology, 2009,37(2):179-182.

(责任编辑 郭金光)

Optimization of power system reactive power planning based on dynamic NW small world quantum particle swarm algorithm

CHEN Zhijiang, PENG Zuqun, CHEN Yucheng

(Faculty of Automation , Guangdong University of Technology ,Guangzhou 510006 , China)

The paper proposed a dynamic NW small-world quantum particle swarm algorithm (NWQPSO) to solve problems in the optimization of power system reactive power planning. The NW small-world dynamic topological structure was applied to the particle formula of evolution, increasing the diversity of particles in the iterative process, which enabled local search and global search. The voltage stability margin index was used to search for the nodes of system with relatively weak voltage stability, where reactive power compensation would be installed. Taking reactive power compensation device investment and the network loss comprehensive cost as objective function, the effectiveness of planning method and the algorithm is verified through IEEE30 nodes system optimization simulation.

reactive power planning optimization; static voltage stability margin index; NW small-world; quantum particle swarm

2015-08-21。

陈志江(1990—)，男，硕士研究生，研究方向为智能算法在电力系统中的应用。

广东省自然科学基金项目(S2013040013776)

TM714.3

A

2095-6843(2015)05-0390-05