基于改进云自适应遗传算法的无功优化

徐刚刚

(国网河南省电力公司洛阳供电公司,河南 洛阳 471023)

基于改进云自适应遗传算法的无功优化

徐刚刚

(国网河南省电力公司洛阳供电公司,河南 洛阳 471023)

遗传算法存在着早熟的现象,易陷入局部最小点,为了克服这个缺点,笔者提出改进云自适应遗传算法(improved cloud adaptive genetic algorithm,ICAGA),即将云模型引入遗传算法,由X条件发生器自适应调整交叉变异概率,使交叉变异概率既具有传统自适应遗传算法的趋势性,满足快速寻优,又具有随机性,改善避免陷入局部最优能力,然后用模拟农夫捕鱼算法(SFOA)中的收缩搜索来对云自适应遗传算法进行修正,以获全局最优解。以网损最小为目标函数,对标准IEEE 14和IEEE 30节点系统进行仿真计算,结果表明该算法能够获得更好的优化解。

云理论; 网损最小; 云自适梯度遗传算法; 无功优化

电力系统的无功优化是指在网络结构参数及负荷给定的情况下,通过调节控制变量(发电机的端电压、有载调压变压器变比、无功补偿装置的档位)及充分利用电力系统的无功电源,改善电压质量,减小网络损耗。无功优化是典型的非线性规划问题,具有非线性、多目标、多约束、同时含有连续变量和离散变量等特点。传统的无功优化算法有:线性规划法(LP)、非线性规划法(NLP)、动态规划法(DP)等,但是传统的算法具有很大的局限性,对离散变量的处理也有些不当,所以近年来出现了很多智能算法,如模拟退火算法(SA)[1]、免疫算法(IA)[2]、混沌优化理论、遗传算法(GA)[3]、粒子群优化算法(PSO)[4]等。大家知道传统的遗传算法因为交叉和变异概率是定值,所以有很多缺点,如早熟收敛,易陷入局部最优,而且若要取得较好的解需要经过反复的试验来设定这两个参数；自适应遗传算法(AGA)虽然交叉变异概率自适应产生,在收敛速度上比遗传算法要好,但是易陷入局部极值。而云理论是对模糊控制理论隶属函数概念的创新和发展,已成功用于智能控制[5]、数据挖掘[6]等领域。因此,本文提出了改进云自适应遗传算法,即将云模型引入遗传算法,利用了云滴的随机性和稳定倾向性的特点,由云模型的X——条件云发生器,根据适应度函数值的大小自适应产生交叉变异概率,使概率值满足两种特性:一是具有AGA算法的趋势性,满足快速寻优能力；二是具有云模型的随机性,在适应度值最大时不取绝对的零值,从而大大的改善了避免陷入局部寻优的能力,然后用模拟农夫捕鱼算法[7](SFOA)中的收缩搜索对CAGA算法进行修正,以获全局最优解。通过算例分析，验证了该方法可行性。

1 无功优化的数学模型

本文从经济性角度出发,以系统的有功网损最小作为优化目标,其优化模型可表示为

(1)

式中:NK为支路集合;Gk(i,j)为支路k的电导;θij为节点i与节点j之间的电压相角差。

等式约束条件为:

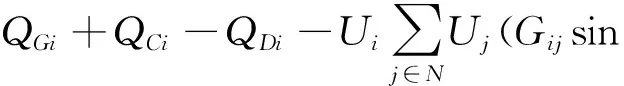
i∈NPQ

(2)

式中:QGi、QCi、QDi分别为发电机节点注入无功功率、负荷节点无功功率和补偿节点的补偿无功功率;NPQ为PQ节点的集合;Gij和Bij为节点导纳阵的系数;θij同式(1)。

不等式约束条件:

1) 控制变量约束有:

(3)

式中:UGi、UGimax、UGimin分别为发电机的端电压及上、下限;QCi、QCimax、QCimin分别为无功补偿容量及上、下限;Tki、Tkimax、Tkiminx分别为变压器分接头的位置及上、下限;NG、NC、NT、N分别为发电机节点数、补偿电容器节点数、变压器支路数和总的节点数。

2) 状态变量约束有:

(4)

式中:QGi、QGimax、QGimin分别为发电机无功出力及上、下限;Ui、Uimax、Uimin分别为负荷节点i的电压及上、下限;NG、N分别为发电机节点数和总的节点数。

在不等式约束中,状态变量不等式约束以惩罚项形式处理,则目标函数式(1)构成一个新的目标函数f,可表示为

(5)

(6)

(7)

2 改进云自适应遗传算法

2.1 基本遗传算法

遗传算法的基本流程如下:

1) 初始化种群,设置相关参数,对个体进行编码;

2) 设计一个适应度函数,对种群中的个体进行评估;

3) 进行选择、交叉和变异等遗传操作;

4) 判断是否到达最大进化代数,如到达,则停止进化,输出最优解,否则转到步骤(2),继续进化。

2.2 云理论

2.2.1 云模型

云模型由李德毅等人提出[5],是一种定性知识描述和定型概念与其定量数据之间的不确定性转换模型,主要反映客观世界、人类知识等领域中概念的模糊性和随机性。

定义1:云和云滴[6]，设U为用数值表示的定量论域,C是U上的定性概念,映射u:U→[0,1],∀x∈U,x→u(x),其中,定量值x∈U是定性概念C的一次随机实现,u(x)∈[0,1]是x对C的确定度,它是一个随机数,具有稳定倾向性,则x在论域U上的分布称为云,记为云C(x),x就称为一个云滴。

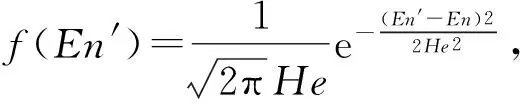
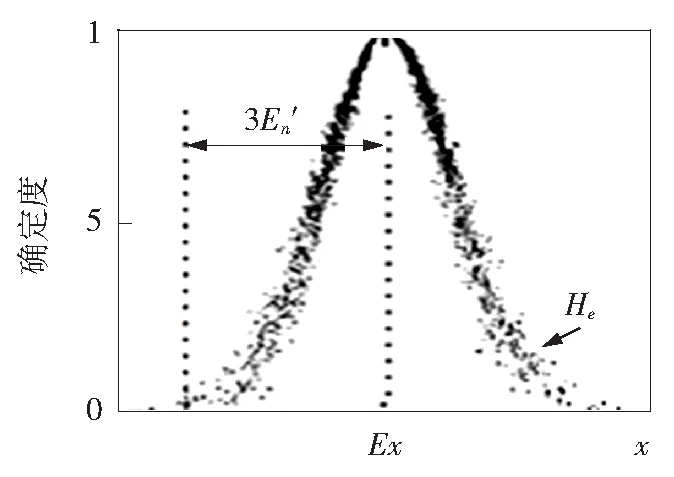
图1 正态云模型的三个参数

2.2.2 云发生器

本文要用到的云发生器是X-条件云发生器[8]。

X-条件云发生器是指给定云的三个参数(Ex,En,He)和论域U上的某个值x0产生云滴(x0,u)的云发生器。

input: {ExEnHe},n,x0//参数和云滴数

output: {(x0,u1),…(x0,un)}://生成符合条件的云滴

fori=1 ton

drop(x0,u)

2.2.3 云自适应遗传算法的步骤

云自适应遗传算法的具体步骤如下:

1) 云自适应交叉概率新算法步骤:

He=En/c2

En′=RANDN(En,He)

2) 云自适应变异概率新算法步骤:

Ex=f

En=(fmax-f)/c3

He=En/c4

云自适应交叉和变异概率如图2所示。

2.3 收缩搜索

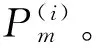
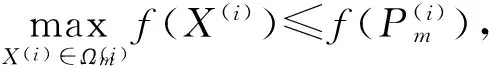
式中:

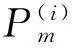
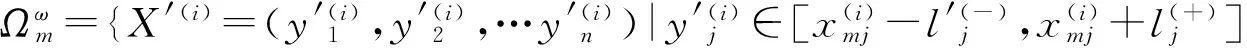
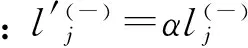
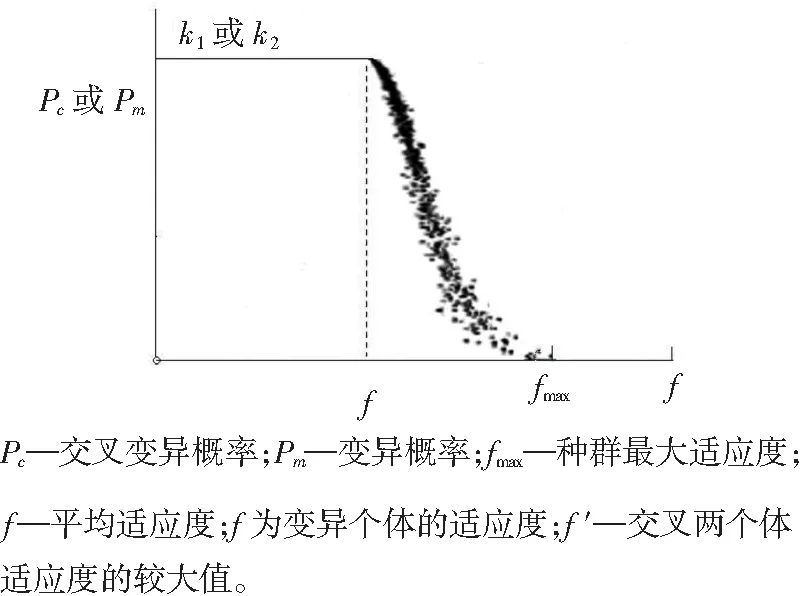
图2 云自适应交叉率Pc、变异率Pm

2.4 改进云自适应遗传算法的流程图

把收缩搜索的思想引入云自适应遗传算法,从而提出改进云自适应遗传算法,其流程如图3所示。

图3 改进云自适应遗传算法的流程图

Fig.3 Flow chart improving cloud adaptive

genetic algorithm

3 算例分析

3.1 典型函数优化仿真

3.1.1 测试函数

验证算法的性能,本节选取4个典型的函数进行仿真测试,验证算法的有效性和优越性。

f1:Ackley函数

-15≤xi≤30；i=1,2,…,n.

函数f1的最优状态和最优值分别为点X*=(0,0,…,0)和f1(X*)=0

f2:Beale函数

-4.5≤xi≤4.5；i=1,2

函数f2的最优状态和最优值分别为点X*=(3,0.5)和f2(X*)=0

f3:Branin函数

-5≤x1≤10, 0≤x2≤15

函数f3的最优状态和最优值分别为点X*=(-π,12.275),(π,2.275),(9.424 78,2.475)和f3(X*)=0.397 887

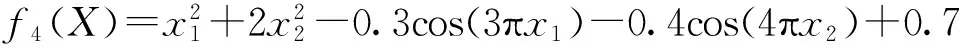
-100≤xi≤100；i=1,2；f4(X*)=0

函数f4的最优状态和最优值分别为点X*=(0,0)和f4(X*)=0

3.1.2 仿真结果

对以上4个典型测试函数分别用GA算法和ICAGA算法进行10次函数优化实验,并对实验结果进行分析。算法参数分别设为:种群规模均为100,最大进化代数也均为100,终止条件是最大进化代数;其中GA的Pc=0.9,Pm=0.1。仿真结果的两种算法性能对比如表1所示。函数仿真对比如图4—图7所示。

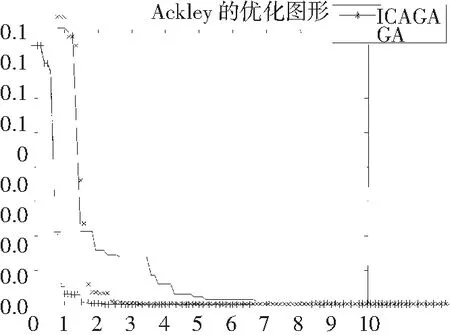
图4 Ackley函数仿真对比图

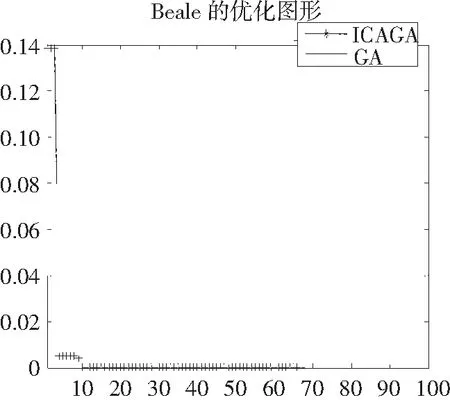
图5 Beale函数仿真对比图

图6 Bohachevsky函数仿真对比图

图7 Branin函数仿真对比图

Fig.7 Branin function simulation comparison chart

从表1和图4～7可以看到,对f1和f3,ICAGA在计算精度上要优于GA,ICAGA在收敛速度上也要优于GA;对于f2,ICAGA算法依然表现了良好的收敛性能;对于f3,在仿真实验中,GA完全不能收敛;此时ICAGA在精度和跳出局部搜索能力上的优势明显得以体现,几乎达到了零误差,取得了非常好的收敛速度和计算精度。

3.2 IEEE-14和IEEE30节点系统仿真

在相同条件下,分别在IEEE14和IEEE30节点系统运行标准GA(遗传算法)、AGA(自适应遗传算法)、CAGA(云自适应遗传算法)和ICAGA(改进云自适应遗传算法),网损优化曲线如图8、图9所示。

图8 IEEE14节点系统GA、AGA、CAGA和ICAGA算法优化曲线比较

Fig.8 IEEE14 node system GA, AGA, CAGA and algorithm optimization curve ICAGA

从图8、图9可以看出,ICAGA算法的收敛速度和收敛精度都优于另外3种算法,ICAGA算法的收敛性更佳,能够跳出局部最优解,比另外3种算法更加接近全局最优解。电压曲线比较如图10和图11所示。

从图10和图11可以看出ICAGA算法的电压曲线更趋合理,没有电压越限。

对4种算法分别进行10次计算,得到目标函数的优化解如表2和表3所示。表中网损数据为标幺值,基准功率为100 MVA。

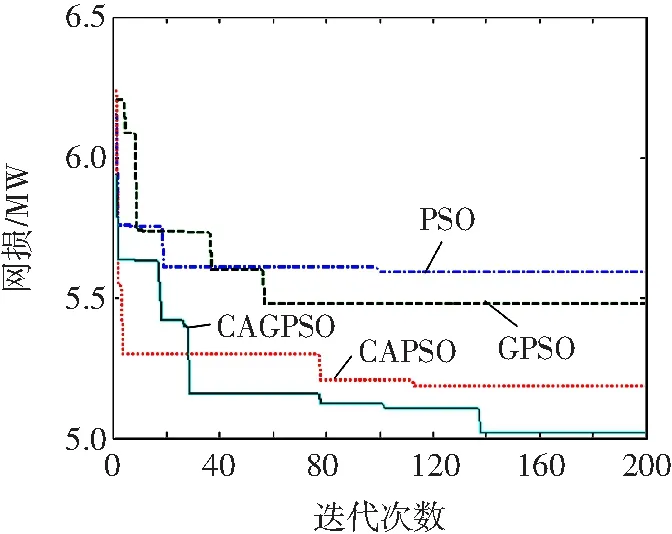
图9 IEEE30节点系统GA、AGA、CAGA和ICAGA算法优化曲线比较

Fig.9 IEEE30 node system GA, AGA, CAGA and algorithm optimization curve ICAGA

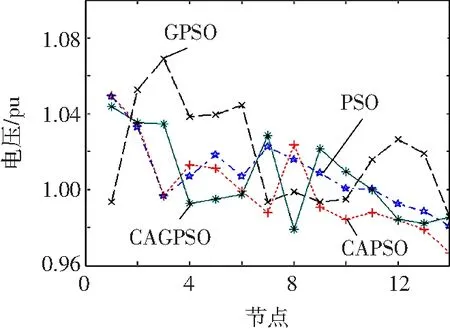
图10 IEEE14节点系统GA、AGA、CAGA和ICAGA算法电压曲线比较

Fig.10 Comparison voltage curve of AGA GA CAGA and ICAGA algorithm in IEEE14node system

图11 IEEE30节点系统GA、AGA、CAGA和ICAGA算法电压曲线比较

Fig.11 Comparison voltage curve of GA CAGA AGA, and ICAGA algorithm in IEEE30node system

从表2、表3可以看到,ICAGA计算得到的平均网损小于另外3种算法,能够跳出局部最优解,更加接近目标函数的全局最优解。

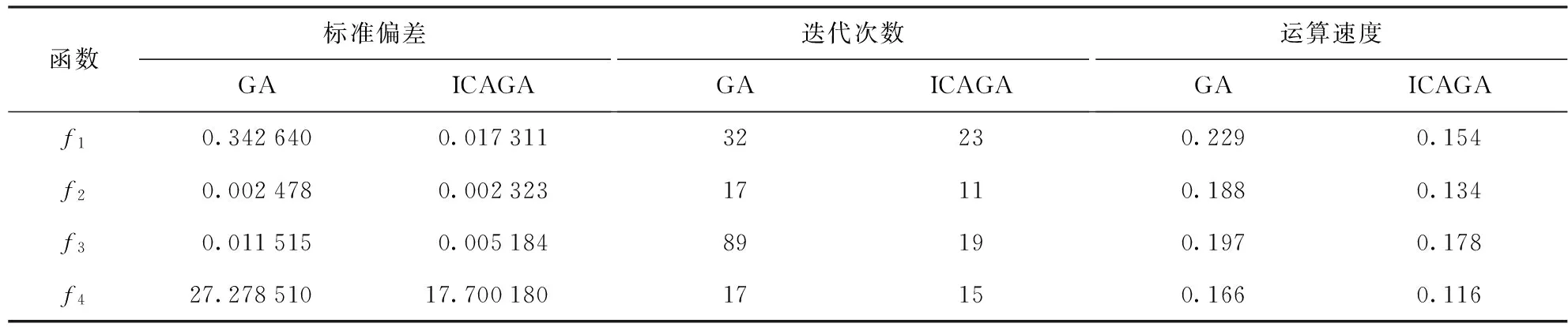
表2 IEEE-14节点系统4种算法网损计算结果对照

Tab.2 Comparing calculating results of network loss by 4 algorithms in IEEE-14 node system

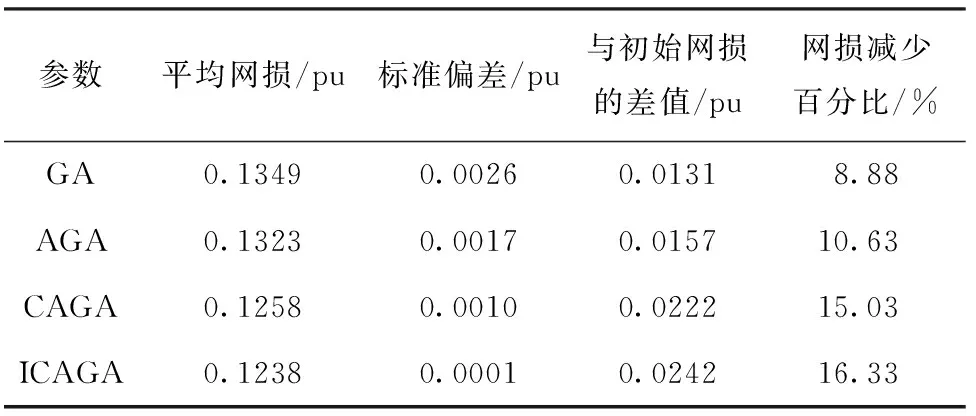
参数平均网损/pu标准偏差/pu与初始网损的差值/pu网损减少百分比/%GA0.13490.00260.01318.88AGA0.13230.00170.015710.63CAGA0.12580.00100.022215.03ICAGA0.12380.00010.024216.33

表3 IEEE-30节点系统4种算法网损计算结果对照

Tab.3 Comparing calculating results of network loss by 4 algorithms in IEEE-30 node system

参数平均网损/pu标准偏差/pu与初始网损的差值/pu网损减少百分比/%CA0.55400.00040.00183.18AGA0.05120.00050.006010.46CAGA0.05330.00040.00396.80ICAGA0.05030.00050.006912.09

4 结 论

1) 改进云自适应遗传算法(ICAGA)是在传统的遗传算法的基础之上引入云理论,由X条件发生器自适应调整交叉变异概率,使交叉变异概率既具有传统AGA的趋势性,满足快速寻优,又具有随机性。当种群适应度最大时并非绝对的零值,有利于提高种群多样性和改善避免陷入局部最优的能力,然后用模拟农夫捕鱼算中的收缩搜索来对云自适应遗传算法进行改进。

2) 通过4个典型测试函数,及以网损最小为目标函数,对标准IEEE14节点系统和IEEE30节点系统进行仿真计算,结果表明ICAGA算法在跳出局部最优解,寻找更好的全局最优解方面有很大的优势,收敛性能好,解的质量高,较稳定。同时在进一步降低网损方面,具有很强的实用性和可行性。

[1] 白云,徐刚刚,宋阳. 基于改进社会认知算法的电力系统多目标无功优化[J].黑龙江电力,2012,12(1):21-24. BAI Yun, XU Ganggang, SONG Yang. Multi-objective reactive power optimization based on modified society cognitive optimization for electric power system [J]. Heilongjiang Electric Power, 2012, 12(1):21-24.

[2] 祝洪博,徐刚刚,海冉冉，等.基于云自适应梯度粒子群算法的无功优化 [J].电网技术,2012,31(2):51-56. ZHU Hongbo, XU Ganggang, HAI Ranran, et al. Reactive power optimization based on cloud adaptive gradient particle swarm optimization [J]. Power System Engineering, 2012,31(2):51-56.

[3] 海冉冉.《基于云自适应遗传算法的优化问题研究》[M]. 吉林：东北电力大学,2013. HAI Ranran. Research on the optimization based on cloud adaptive genetic algorithm [M]. Jilin:Northeast Dianli University, 2013.

[4] 袁晓辉,王乘,张勇传,等.遗传优化算法在电力系统中的应用[J].电网技术,2004,28(19):14-19. YUAN Xiaohui, WANG Sheng, ZHANG Yongchuan, et al. Application of genetic algorithm in power system [J]. Power System Engineering, 2004,28(19):14-19.

[5] 李德毅,杜鹢.不确定性人工智能[M].北京:国防工业出版社,2005. LI Deyi, DU Yi. Artificial intelligence with uncertainty [M]. Beijing: National Defend Industry Press, 2005.

[6] 李德毅,孟海军,史雪梅.隶属云和隶属云发生器[J].计算机研究与发展1995(6):15-20. LI Deyi, MENG Haijun, SHI Xuemei. Membership clouds and membership cloud generators [J]. Computer R&D, 1995(6):15-20.

[7] 陈建荣. 群智能优化算法研究及其应用[D], 广西：广西民族学院,2009. CHEN Jianrong. Study and application of warm intelligence optimization [D]. Guangxi:Guangxi University for nationalities, 2009.

[8] ZHU Yunfang,DAI Chaohua,CHEN Weirong,et al.Adaptive probabilities of crossover and mutation in genetic algorithm based on cloud generators[J].Journal of Computational Information Systems,2005,1(4):671-678.

(责任编辑 郭金光)

Reactive Power Optimization Based on ICAGA Algorithm

Xu Ganggang

(Luoyang Power Supply Company of State Grid Henan Electric Power Company, Luoyang 471023, China)

Genetic algorithm (GA) has the defect of prematurity during the optimization process which makes it easy to fall into the local minimum. To cope with this defect, the author proposes improved cloud adaptive genetic algorithm (ICAGA). Bying applying GA in the cloud model, the adaptive adjustment of the crossover and mutation probability can be done by X condition generator, which enjoys both traditional AGA trend and the fast optimization with randomness. The algorithm can aslo improve the capacity to avoid falling into local optimal. Then the idea of shrinking search in the Simulating Fisher fishing Optimization Algorithm (SFOA) is brouhgt in to obtain the global optimaization. Taking the minimum network loss as objective function, the simulation for the proposed ICAGA algorithm by standard IEEE 14-bus system and IEEE 30-bus system are performed. The simulation results show that the better optimal solution can be attained by the proposed ICAGA algorithm.

cloud theory; minimum network loss; cloud adaptive genetic algorithm; reactive power optimization

2015-02-23。

徐刚刚(1985—),男,硕士，工程师,研究方向为电力系统优化、继电保护。

TM714

A

2095-6843(2015)04-0347-06