无线传感器与执行器网络基于邻居信息的割点检测算法*

李修琪，杨 杰，冯 勇，王 翊

（昆明理工大学云南省计算机技术应用重点实验室，昆明650500）

无线传感器与执行器网络WSANs（Wireless Sensor and Actuator Networks）是在无线传感器网络WSNs的基础上发展起来的一种新型的无线自组织网络［1-2］。WSANs拥有一定数量的可自主移动的执行器，具有可作用于环境、能够实时响应环境变化等传统无线传感器网络并不具备的优点。

WSANs中普通传感器节点能量、计算、存储和通信能力都有限且节点不可移动，而执行器节点则是可移动的，具有更多的能量，更强的计算、存储和通信能力［3］。WSANs中可以通过执行器节点的移动来实现网络的最佳性能［4］，也可以在传感器节点出现问题的时候将执行器节点移动到问题节点处进行拓扑修复，以提高网络的鲁棒性、保证网络的性能。

割点（cut vertex），是无线传感器与执行器网络中一旦失效就会引起网络分割的关键节点，是因为网络中节点随机分布可能产生的瓶颈节点［5］。割点的失效可能会引起无线传感器网络区域性的通信中断，影响网络的信息收集和传送功能。而且由于无线传感器网络中的节点能量有限，一旦割点失效还将影响到传感器的能量优化从而增加整个网络的能量消耗，缩短WSANs的生命周期［6］。因此，在WSANs中，准确的割点检测机制是实现拓扑修复以增强网络鲁棒性的重要基础。

本文提出了一种基于邻居信息进行割点检测的分布式算法，该算法中每个节点通过与距离自身至多两跳邻居节点进行信息交换建立局部的网络拓扑信息并分析WSANs网络拓扑中的环和折线，然后根据判定规则判断节点是否为割点。试验模拟发现DCVN能很好的完成割点检测的任务，相较之前的几种割点检测算法，准确率有所提高。

1 相关工作

早在2004年，割点的定义首先被Milenko Jorgic'等人提出［7］，此后的十多年中人们尝试利用图论，连通支配集，关键点等各种各样的工具来寻找割点，但是割点检测的准确率和命中率仍有待提高。

Muhammad Imran等人提出的DCR算法［8］中，每个执行器节点通过邻居节点的位置信息来判断自身是否为割点。根据节点位置计算节点间距离来判断两个节点是否相邻。最后，如果节点的所有一跳邻居节点都能相互连通，则该节点为普通节点，否则就是割点。该方法实现简单，但是判断是割点的条件比较苛刻，会有一部分割点无法检测出来。割点判别的准确率高但是漏检率也较高。

文献［9］提出了一个构造连通支配集来寻找割点的算法。首先介绍了形成连通支配集的算法，然后提出了一个减小支配集的支配集修剪规则。文献［10-11］把属于连通支配集的节点称为支配者，把与连通支配集相邻的节点称作被支配者。根据支配者与被支配者的关系来判定是不是割点，但是该割点检测算法的准确率还有待提高。

文献［12］提出了一个基于有限拓扑信息的关键节点和非关键节点的分离算法（LASCNN）。每个节点创建并维护一个k跳连接列表，列表包含了k跳内的所有节点。每个节点顺次反复遍历自己的连接列表，最后创建一个k跳连接的邻居列表。如果k跳连接邻居列表包含所有的k跳邻居节点，则该节点是普通节点，否则为割点。该算法已经能够做到对割点比较准确的检测。

DCVN算法采用了根据邻居信息进行拓扑匹配的割点判决思路。首先，我们将无线传感器与执行器网络划分成5种基本的拓扑结构并总结出割点的判定规则。然后，在权衡准确性与算法复杂度的基础之上取了至多两跳的邻居信息来进行割点的检测。

2 对网络拓扑的基本划分

在WSANs中，相邻节点之间通过定期发送“心跳”消息［13］来交换彼此的状态信息（路由信息，能量状态，地理位置等）。一旦不能收到某个邻居节点的“心跳”消息，我们就认为该节点因为某些原因失效。据此我们可以判断节点是否正常工作。

图1是一个无线传感器与执行器网络拓扑图，图中连线表示两节点能够正常交流“心跳”信息，互为邻居关系。

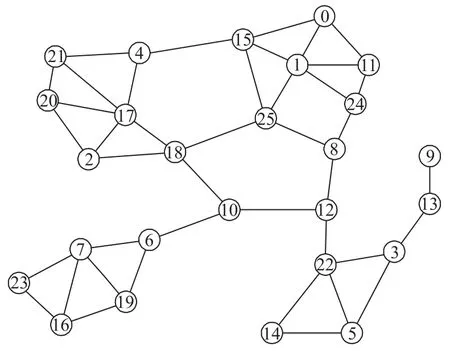
图1 一个WSANs的拓扑结构

对图1的拓扑结构进一步分析，我们可以得出以下结论：无论网络中节点数量有多少，网络拓扑由三种最基本的元素构成，就是环、折线和孤立节点。环是指由两个以上节点所组成的起点和终点相同的结构。折线是指两个及以上节点组成的线型结构。孤立节点是指没有邻居节点的单独节点。

我们将环、折线、孤立节点这三种元素的所有组合方式概括为5种：环组合方式，折线组合方式，孤立节点组合方式，环与环相交的组合方式，环与折线的组合方式，如图2所示。

图2 网络拓扑的5种基本划分

根据割点的定义可知：环上的节点都是普通节点；折线上的节点除了叶子节点之外都是割点；叶子节点和孤立节点是普通节点；环与环相交处的节点以及环与折线相交处的节点是割点。

3 割点的判定规则

结合上述5种组合方式以及文献［14］和［15］中的割点判别方法，本文总结出如下割点判定规则：

①如果Ai是叶子节点或者孤立节点，则Ai是普通节点（如图2（C）中节点6，图1中节点9）。

②如果Ai与他所有的一跳邻居节点能够形成一个环，或者Ai的所有一跳邻居能够自己组成一个环，则Ai是普通节点（如图2（A）中节点2，图1中节点1）。

③如果Ai与他的部分一跳邻居节点能够形成一个环，与部分的邻居节点连成折线，这些环和折线包含了所以的一跳邻居，并且这些折线中至少有一条折线的一跳或二跳邻居节点是叶子节点或割点，则Ai是割点（如图2（E）中节点0）。

④如果Ai能够组成两个或两个以上的环，这些环包含了所有的一跳邻居节点并且环与环之间没有公共节点，则Ai是割点（如图2（D）中节点2）。

⑤如果Ai能够组成两个或两个以上的环和若干条折线，所有的一跳邻居节点不能组成环，折线中至少有一条折线的一跳或二跳邻居节点是叶子节点或割点，则Ai是割点（如图1中的节点22）。

⑥如果Ai与一跳邻居不能组成环，但是Ai有若干条折线，并且存在至少一条折线的一跳或二跳邻居节点是叶子节点或割点，则Ai是割点（如图2（E）中节点3，图1中节点12）。

4 算法的具体实现

DCVN中节点分别对收集到的距自身两跳和四跳之内的邻居列表顺次遍历得出相应的环、折线和孤立节点进而判断自己是割点还是普通节点。DCVN算法分为三步：第一步，收集两跳邻居列表；第二步，挖掘本地信息做判断，第三步，询问邻居节点做判断。

4.1 收集两跳邻居列表

用到的节点命名规则：

Ai：需要判断自身是否为割点的节点。

AiNj_1hop：距Ai一跳的邻居节点。

AiNj+1_1hop：距Ai的不同于AiNj_1hop的其他一跳邻居节点。

AiNjNk_2hop：距AiNj_1hop一跳的邻居节点（即距Ai两跳的邻居节点）。

AiNj+1Nk_2hop：距AiNj+1_1hop一跳的邻居节点（即距Ai两跳的邻居节点）。

我们知道，相邻的节点可以通过发送“Hello”消息来收集彼此包括ID在内的状态信息。DCVN的两跳邻居列表收集可以分为两步：

①节点Ai发送“Hello”消息给一跳范围内所有邻居节点，收到消息的一跳邻居节点AiNj_1hop返回一条ACK消息给节点Ai。

这一步可以收集节点Ai的一跳邻居列表，然后保存到一跳邻居列表listAi_1hop中。

例如，图1中节点A12有三个邻居节点：A8、A10、A22，则A12可收集一跳邻居列表如表1所示。

表1 节点A12的一跳邻居列表listA12_1hop

②节点Ai的一跳邻居节点AiNj_1hop也广播“Hello”消息来收集自身的一跳邻居列表。然后Ai与AiNj_1hop交换自己的一跳邻居列表。这样，Ai能收集到距自身两跳的邻居节点信息，AiNj_1hop能收集到距自身一跳的部分邻居节点信息。

经过这两步，节点Ai就在本地存储了距自身一跳和两跳的节点列表，DCVN就是利用这些信息实现割点检测。

表2 节点A10的两跳邻居列表listA10_2hop

下面以图1中的节点A10为例来进行说明。首先，A10发送“Hello”消息给一跳邻居节点A6、A12、A18，这三个一跳邻居节点收到“Hello”消息后返回ACK消息。与此同时，A6、A12、A18等节点也会发送它们自己的“Hello”消息来收集它们自己的一跳邻居列表。接下来第（2）步中，A10与A6、A12、A18交换自身的一跳邻居列表。经过这两步之后A10就收集到了距自身两跳的邻居节点列表（A10删除与自身ID相同的两跳节点），如表2所示。

节点Ai收集到自身的两跳邻居列表后，通过挖掘这些邻居列表获得拓扑中的环与折线，然后依照割点判定规则判断自己是割点还是普通节点。

4.2 挖掘本地信息做判断

挖掘本地信息是指节点依次遍历自身的一跳和两跳邻居列表，并寻找列表中具有相同ID的节点，从而找出拓扑结构中由3个或4个节点组成的环和由3个节点组成的折线。具体的步骤如下：

（1）节点Ai先读取自己的一跳邻居节点列表做判断。

①如果Ai没有一跳邻居节点，则Ai是孤立节点，非割点。

②如果Ai有唯一的一跳邻居节点，则Ai是叶子节点，非割点。

③如果Ai有两个或两个以上的一跳邻居节点。则取一跳邻居节点AiNj_1hop，将AiNj_1hop的一跳邻居AiNjNk_2hop的ID依次与Ai的其他一跳邻居AiNj+1_1hop进行对比。如果ID相等，说明Ai、AiNj+1_1hop、AiNjNk_2hop3个节点组成一个环，将组成环的节点ID存储到环列表中，跳转到第（3）步。如果ID不相等，则将节点ID存储到表示折线的列表中，跳转到第（2）步。

（2）将AiNj_1hop的一跳邻居AiNjNk_2hopID依次与AiNj+1_1hop的一跳邻居AiNj+1Nk_2hopID进行对比。如果ID相等，则Ai、AiNj_1hop、AiNjNk_2hop、AiNj+1_1hop4个节点组成一个环，将组成环的节点ID存储到表示环的列表中，并跳转到第（3）步。如果ID不相等，就将节点ID存储到表示折线的列表中，也跳转到第（3）步。

（3）继续用AiNj_1hop的一跳邻居AiNjNk_2hop执行第（2）步，直到AiNj_1hop的一跳邻居列表遍历完毕。在Ai重复执行上述步骤时，如果AiNjNk_2hop的ID与Ai或AiNj_1hop的ID相等则直接跳过（1）（2）步，继续遍历下一个节点，因为该环已经被遍历记录过。

（4）继续用Ai剩余的一跳邻居节点执行上述三步，直到Ai的一跳邻居节点遍历完毕。

（5）将前面四步得到的环的节点ID相互进行对比。如果环包含了折线的所有点，则删掉该折线；如果环与环之间有两个及两个以上的公共节点，则两个环合并为同一个环。

经过以上五步，节点Ai依个点判定规则能够判断出由3个或4个节点组成的环和不超过3个节点的折线中的节点是割点还是普通节点。如果仍旧无法判断出自己是否是割点则继续执行后续的询问邻居节点部分。

挖掘本地信息是DCVN最基本最重要的一步，此处以图1中节点A25为例说明挖掘本地信息的过程。首先，A25读取两跳邻居信息，得到自己及一跳邻居的一跳邻居列表（表3）。首先，A25读取第一个一跳邻居节点A1所对应的一跳邻居列表中的A0，再将A0的节点ID分别与A25的其余的一跳邻居节点A8、A18、A15的ID进行对比，ID不相等，此时第一步执行完毕。第二步，A25将A0的节点ID分别和A8、A18、A15的一跳邻居列表（即A25的二跳邻居节点ID）进行对比，发现A0的ID和A15的一跳邻居列表中的某个节点的ID相等而其他A25的两跳邻居列表中没有与A0相同的节点，所以判定只有A25、A1、A15、A0这4个节点组成环并记录到环的列表中。接下来执行第三步，A25读取A1所对应的一跳邻居节点A11，并重复执行第一步和第二步。由于没有节点与A11的ID相等，所以A25保存A25、A1、A11这3个节点组成的折线到折线列表中。

按以上方法遍历A15、A1、A8、A18，能够得到表4。在遍历完所有的一跳邻居之后，A25对得到的环和折线进行合并处理最后，A25得到的挖掘本地信息表如表5所示。

表3 A25、A1、A15、A8、A18的一跳邻居列表

表4 节点A25合并之前构成的环与折线

表5 节点A25合并之后构成的环与折线

根据表4的信息，A25暂时不能判断自己是割点还是普通节点，所以A25继续执行DCVN算法后面的询问邻居节点部分的算法。

在执行完毕挖掘本地信息的过程后，虽然A25还不能推断出自己是否是割点，但是有一部分节点已经可以判断出自己是割点还是普通节点。图1所示的拓扑结构在执行完挖掘本地信息过程后，得到的拓扑结构如图3所示，黑色填充节点是割点，灰色填充节点是暂时不能做出判断的节点。

4.3 询问邻居节点做判断

假如Ai经过上一步还不能判断自己究竟是割点还是普通节点则Ai继续向自己的部分第二跳邻居节点AiNjNk_2hop发送请求消息，请求AiNjNk_2hop发送自身的两跳邻居列表给Ai。Ai根据收到的消息进一步判断自己是否为割点。询问两跳邻居节点其实就是要分析得出大于4个节点组成的环。Ai的询问两跳邻居节点部分分为以下4步：

①Ai发送请求消息，获取Ai的两跳节点AiNjNk_2hop的两跳邻居列表（也就是距Ai三跳或四跳的邻居列表）。

我们把Ai的一跳邻居节点AiNj_1hop分成两类，一类AiNj_1hop是组成环的一部分。另一类AiNj_1hop不是环的一部分（即是折线的一部分）。Ai只向第二类AiNj_1hop的一跳邻居AiNjNk_2hop发送请求，获得AiNjNk_2hop的两跳邻居列表，但是这两跳邻居不能包括回溯的点，即AiNjNk_2hop的一跳邻居需要把AiNj_1hop排除在外。

例如，图3中的节点A25发送请求消息给A2、A17、A10，请求A2、A17、A10发送两跳邻居列表给A25。但是A25不发送请求消息给A11、A12、A4，因为A11、A12、A4所对应的A1、A8、A15已经是上一步中挖掘本地信息部分得到的环的组成部分。

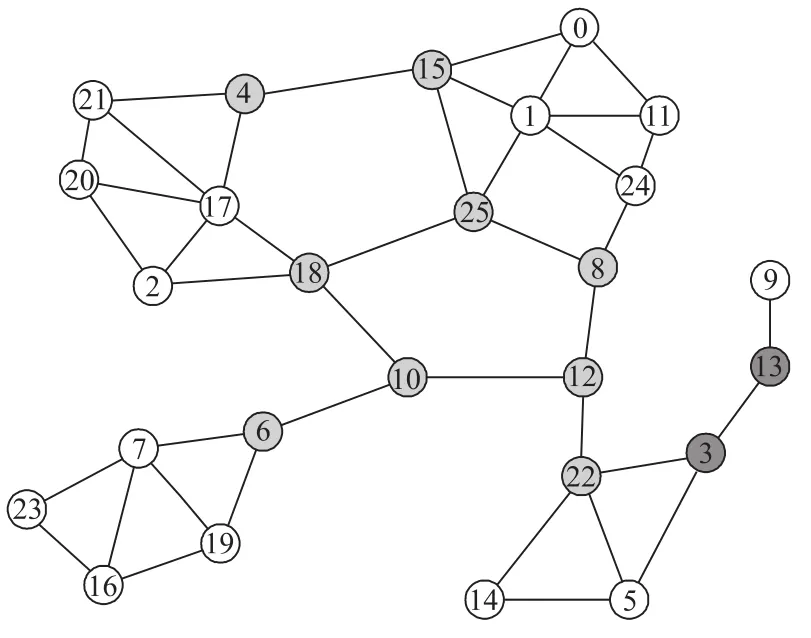
图3 DCVN挖掘本地信息后的割点分布

②）Ai根据收到的AiNjNk_2hop两跳内的邻居节点信息，分析已知信息中是否还有环存在。Ai首先将第一步得到的两跳邻居AiNjNk_2hop中的一跳和二跳节点ID与挖掘本地信息部分得到的折线的第三个节点（即Ai的二跳邻居节点）ID进行对比，如果相等，说明相关联的这些节点能组成一个环将他们存入Ai的环列表，否则，转到第（3）步。

③Ai将第一步得到的两跳邻居AiNjNk_2hop中的一跳和二跳节点ID相互对比，也与其他的两跳邻居AiNjNk+1_2hop的一跳和两跳邻居进行对比。如果有相等的节点就说明Ai、AiNj_1hop、AiNjNk_2hop这条折线之后有环存在；如果不相等的节点就认为此条折线之后是叶子节点。依次遍历对比Ai的所有两跳节点的后续两跳节点。

④将的Ai环列表中的环与环进行对比，折线与折线进行对比。如果有重复的环则删掉多余的；如果环与环之间有两个或两个以上的公共节点，则这两个环合并为一个环。如果有能覆盖短折线的更长折线则取最长的那条折线。

经过以上三步节点Ai能够得到节点数量超过4个少于9个的环，此时可以再次根据割点判定规则进行判断。此次判断能够判断出由5到8个节点组成的环和4个节点组成的折线中的节点是割点还是普通节点。

经过询问邻居节点的以上四步，对于超过8个节点组成的环和超过5个节点组成的折线我们还是不能得出来，对于依旧不能判断自身是否是割点的DCVN默认为割点。首先，超过8个节点的折线中的节点本来就是割点，所以我们直接判定其为割点。而对于超过8个节点组成的环，首先该节点无法判断出自身是否处于一个环网中。即使该节点处于一个环网中（超过8个节点组成），假如这个节点失效，那么这个环中其他节点间的通信就可能需要迂回很长的距离来实现，在该迂回距离较长的时候会加快该通信路线上节点的能量消耗［16］，所以我们也将这样的节点视为割点。割点判定的整个过程如图4中流程图所示。

例如，图5（A）中，A0能够通过询问邻居节点得到由A0、A1、A2、A3、A4、A5、A6、A7这8个节点组成的环，我们能够判断出A0不是割点。图5（B）中，A0通过询问邻居节点执行DCVN算法，无法判断自身是否处于环中，即A0无法判断自身是不是割点。此时即使A0处于环中，由于环路可能较长（环中节点数大于等于9个）一旦A0断开，其他节点的通信代价较大，需要消耗较多的能量来进行信息的交换，此时我们也将A0看作割点。

图4 割点检测流程图

图5 8个及8个以上节点组成的环

在执行完DCVN算法后，网络拓扑中的节点都能够判断出自己是割点还是普通节点。图3中的拓扑结构执行完DCVN算法后，到的结果如图6所示。其中，白色节点是普通节点，阴影填充节点是割点在算法的成功率方面，除非拓扑结构中存在8个以上节点组成的环，否则DCVN都能够准确的判断出节点到底是割点还是普通节点。

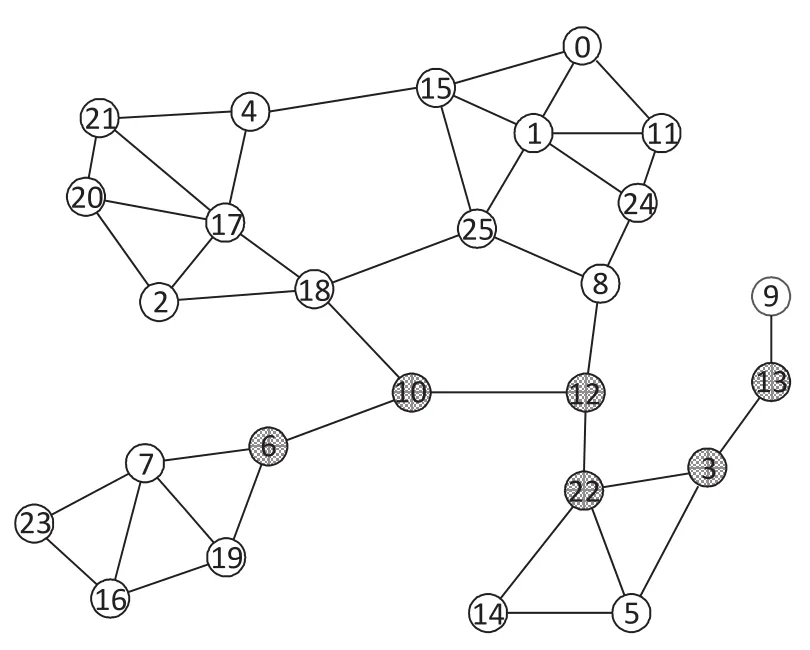
图6 执行完DCVN算法后的割点分布

5 实验模拟及分析

我们在实验中引入了几个指标来衡量DCVN算法性能：

割点占比（Critical Node Ratio）：代表算法检测出的割点的数量占总节点数量的百分比。用于近似衡量网络的连接性和易损坏性，占比越大表明网络的连接性越差，越容易损坏。其中Critical node表示算法成功检测出的割点。由于检测准确率通常不能达到百分之百，因此Critical Node数目小于等于网络中实际存在的割点（cut vertex）数目。

割点检测准确率（Detection Ratio）：代表网络中被正确识别为割点的节点数量占割点实际总数量的百分比。表明了DCVN算法的识别准确率。

部署节点数量（Number of Nodes）：整个网络区域中组成网络的节点数量，反映网络的规模，同时因为实验区域一定，所以网络中节点的密度也在增加。

通信半径（Communication Range）：两个相邻节点能够相互通信的最大距离。网络中的所有节点设为相同的通信半径。

实验模拟在NS-2.35软件上进行，无线传感器与执行器的部署区域设定为1 000 m×1 000 m，节点数量取50、100、150、200、250共五种情况。节点的通信半径设为100、125、150、175、200、225、250共七种情况。节点个数默认150个，节点通信半径默认150 m。

5.1 割点占比

图7中，最大通信半径150 m保持不变。随着网络区域中节点数量的增加，割点占比呈下降趋势。在节点数量从50个增加到150个的过程中，割点占比下降速度较快。对比其他几种割点检测算法，DCVN检测的割点占比较低。随着节点数量的增加，割点占比呈下降趋势。这是因为，随着网络中节点数量的增加，网络中的通信冗余链路必然会越来越多，网络中的割点必然逐渐减少。另外，随着节点数量的增加，在仿真实验的环境中，节点的密度也在增加，即节点之间的平均距离是减少的，节点和节点之间能够相互通信的概率也随之增加，所以割点占比在变小。

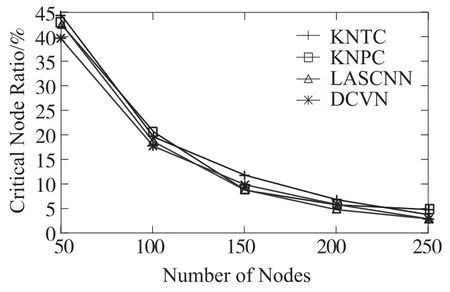
图7 割点占比与节点数量的关系

在图8中，网络区域中节点的数量150保持不变，横坐标是相邻节点之间能够通信的最大半径，纵坐标是割点所占总节点数量的百分比。可以看到，随着最大通信半径的增加，网络中割点所占的比重也越来越小。这是因为随着最大通信半径的增加，原本不能够通信的两节点开始变成邻居节点，就是说就节点的一跳以及两跳的邻居变多了，节点之间能够通信的概率越来越大，通信瓶颈变小，所以网络中的割点数量不断减少，割点占比呈下降趋势。

图8 割点占比与最大通信半径的关系

5.2 割点检测准确率

图9中，最大通信半径保持150 m不变，横坐标表示区域中节点数量，从50个以50为步长逐次增加到250个，纵坐标是割点检测的准确率。割点检测率的变化趋势较复杂，先略微下降再呈缓慢上升趋势。可以看到，DCVN的割点检测率在这几种割点检测算法中是最高的，表明我们的算法可以很好的完成割点检测任务。

图10显示的是在节点数量保持150不变的前提下，割点检测的准确率随着最大通信半径的变化趋势。可以看出，随着通信半径的增加，这4种算法对割点的检测率都是逐渐增大的，DCVN算法只有在通信半径最短的情况下检测率较低，随着最大通信半径的增大，DCVN算的检测率一直是这几种算法中最高的。

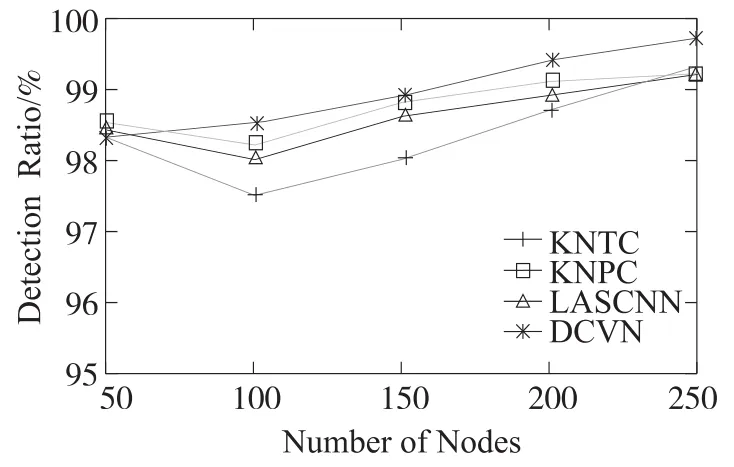
图9 割点检测准确率与节点数量的关系

图10 割点检测准确率与最大通信半径的关系

DCVN是一种分布式算法，收敛速度较快。在通常情况下节点只与其一跳邻居交换信息，此时DCVN算法的时间复杂度为T(n)=O(n2)。在最坏的情况下节点需要与其两跳邻居进行交互，此时DCVN算法的时间复杂度为T(n)=O(n4)。因此DCVN检测准确率的提高是以部分增加算法的时间复杂度为代价的。

6 总结

WSANs不仅能够监测环境中的事件信息而且能够主动改变环境状态以满足用户需求，从而大大拓展了无线传感器网络的能力和应用范围。有效的割点检测算法能够为拓扑修复提供准确的数据，对于提高拓扑修复的效率增强WSANs的鲁棒性有着重要意义。本文提出了一种基于邻居信息进行割点检测的分布式算法DCVN，该算法建立了割点的判别准则，每个节点通过与距离自身至多两跳的邻居节点进行信息交换来建立局部的网络拓扑信息，并基于这些准则分析网络拓扑中的环和折线从而实现割点的检测。仿真实验表明，该算法能够准确识别网络中的割点，与现有几种有代表性的割点检测算法相比DCVN的检测准确率较高。

［1］Melodia T，Pompili D，Gungor V C，et al.Communication and Coordination in Wireless Sensor and Actor Networks［J］.Mobile Computing，IEEE Transactions on，2007，6（10）：1116-1129.

［2］魏春娟，杨俊杰，张志美.一种分布式能量有效的无线传感器网络分簇路由协议［J］.传感技术学报，2013，26（7）：1014-1018.

［3］Amiya Nayak，Ivan Stojmenovic.Wireless Sensor and Actuator Networks Algorithms and Protocols for Scalable Coordination and Data Communication［M］.New Jersey：John Wiley&Sons，2010：15-20.

［4］Wu X，Liu M，Wu Y.In-situ Soil Moisture Sensing：Optimal Sen⁃sor Placement and Field Estimation［J］.ACM Transactions on Sensor Networks（TOSN），2012，8（4）：33.

［5］Xiong S，Li J.An Efficient Algorithm for Cut Vertex Detection in Wireless Sensor Networks［C］//Distributed Computing Systems（ICDCS），2010 IEEE 30th International Conference on.IEEE，2010：368-377.

［6］Liu X，Xiao L，Kreling A.A fully Distributed Method to Detect and Reduce Cut Vertices in Large-Scale Overlay Networks［J］.Computers，IEEE Transactions on，2012，61（7）：969-98

［7］Jorgic M，Hauspie M，Simplot-Ryl D，et al.Localized Algorithms for Detection of Critical Nodes and Links for Connectivity in Ad Hoc Networks［C］//Mediterranean Ad Hoc Networking Workshop，2004：12.

［8］Imran M，Younis M，Said A M，et al.Localized Motion-Based Con⁃nectivity Restoration Algorithms for Wireless Sensor and Actor Networks［J］.Journal of Network and Computer Applications，2012，35（2）：844-856.

［9］Dai F，Wu J.An Extended Localized Algorithm for Connected Dominating Set Formation in Ad Hoc Wireless Networks［J］.Par⁃allel and Distributed Systems，IEEE Transactions on，2004，15（10）：908-920.

［10］Akkaya K，Thimmapuram A，Senel F，et al.Distributed Recovery of Actor Failures in Wireless Sensor and Actor Networks［C］//Wireless Communications and Networking Conference，2008.WCNC 2008.IEEE.IEEE，2008：2480-2485.

［11］Zamanifar A，Sharifi M，Kashefi O.A Hybrid Approach to Actor-Actor Connectivity Restoration in Wireless Sensor and Actor Net⁃works［C］//Networks，ICN’09，2009.

［12］Alnuem M，Zafar N A，Imran M，et al.Formal Specification and Validation of a Localized Algorithm for Segregation of Critical/Noncritical Nodes in MAHSNs［J］.International Journal of Dis⁃tributed Sensor Networks，2014，19：1167-1172.

［13］Zhang Y，Zhang X，Wang Z，et al.Virtual Edge Based Coverage Hole Detection Algorithm in Wireless Sensor Networks［C］//Wire⁃less Communications and Networking Conference（WCNC），2013 IEEE.IEEE，2013：1488-1492.

［14］Gary Chartrand，Ping Zhang著.图论导引.范益政，汪毅，龚世才，朱明，译.人民邮电出版社，2007：93-94.

［15］Xiong S，Li J.An Efficient Algorithm for Cut Vertex Detection in Wireless Sensor Networks［C］//Distributed Computing Systems（ICDCS），2010 IEEE 30th International Conference on.IEEE，2010：368-377.

［16］王越，万洪.一种节能的无线传感器网络多跳自适应时间同步算法［J］.传感技术学报，2013，26（11）：1557-1563.