拟线性抛物方程解的爆破时间下界
2015-03-10卢静
卢 静
(1. 天津大学 理学院 数学系,天津 300072;2. 天津大学 应用数学中心,天津 300072)
拟线性抛物方程解的爆破时间下界
卢 静1,2
(1. 天津大学 理学院 数学系,天津 300072;2. 天津大学 应用数学中心,天津 300072)
研究了下面的方程
ut=Δum+up-uqin Ω×(0,t*),
u(x,t)=0 on ∂ Ω×(0,t*),
u(x,0)=u0(x) in Ω,这里Ω⊂RN是一个光滑有界的开区域且N≥3. 可以得到方程解的爆破时间下界.
拟线性抛物方程;有限时间爆破;爆破时间下界
ut=Δum+up-uqin Ω×(0,t*),
u(x,t)=0 on ∂Ω×(0,t*),
u(x,0)=u0(x) in Ω,
Where Ω⊂RNwas a smooth bounded open domain andN≥3. Obtained the lower bound for the blow-up time of the solution.
本文主要研究的是如下方程解的爆破时间下界,
ut=Δum+up-uqin Ω×(0,t*),
u(x,t)=0 on ∂Ω×(0,t*),
u(x,0)=u0(x) in Ω,
(1)
这里Ω⊂RN(N≥3)是一个光滑有界开区域 ,p,q≥0其中u代表热传导模型中物质的温度.
本文受到了文献[1]的启发而加以延伸.但是我们所研究的是非线性项被吸收的情况. 关于抛物方程解的爆破时间下界有很多相关的结果,可以查阅文献[2-7].
定义
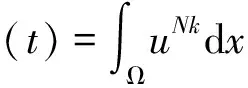
(2)
其中
利用格林公式,得到

(3)
利用Hölder不等式和Yong不等式,我们有

(4)
且0<α<1.利用施瓦兹不等式,得到
(5)
利用Sobolev不等式(见文献[8]),有


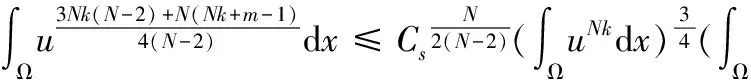
再次利用Yong不等式,得到


(6)
最后得到

其中,
(7)
(8)
(9)
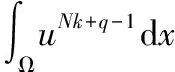
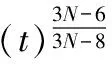
(10)
将式(10)从0到t*进行积分,有
(11)
其中
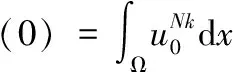
[1] BAO A G, SONG X F. Bounds for the blowup time of the solutions to quasi-linear parabolic problems [J]. Z. Angew. Math. Phys., 2014, 65: 115-123.
[2] LV X ,SONG X . Bounds of the blowup time in parabolic equations with weighted source under nonhomogeneous Neumann boundary condition [J]. Math. Meth. Appl. Sci., 2014, 37: 1019-1028.
[3] PAYNE L E, PHILIPPIN G A, SCHAEFER P W. Blow-up phenomena for some nonlinear parabolic problems [J]. Nonlinear Anal., 2008, 69: 3495-3502.
[4] PAYNE L E, PHILIPPIN G A, SCHAEFER P W.Bounds for blow-up time in nonlinear parabolic problems [J]. J. Math. Anal. Appl., 2008, 338: 438-447.
[5] PAYNE L E, SCHAEFER P W. Lower bounds for blow-up time in parabolic problems under Dirichlet conditions [J]. J. Math. Anal. Appl., 2007, 328: 1196-1205.
[6] L E PAYNE, J C SONG. Lower bounds for the blow-up time in a nonliner parabolic problem [J]. J. Math. Anal. Appl., 2009, 354, 394-396.
[7] SONG X F, LV X S. Bounds for the blowup time and blowup rate estimates for a type of parabolic equations with weighted source [J]. Appl. Math.Comput., 2014, 236: 78-92.
[8] TALENTI G. Best Constant in Sobolev Inequality [J]. Ann. Mat. Pura Appl., 1976, 110: 353-372.
Lower bound for blowup time of solution to quasilinearparabolic equation
LU Jing1, 2
(1. Department of Mathematics, School of Science, Tianjin University, Tianjin 300072, China;2. Center for Applied Mathematics, Tianjin University, Tianjin 300072, China)
In this paper,the following problem were diseussed
quasilinear parabolic equation; blow up in finite time; lower bound for blow-up time
2014-09-17.
卢 静(1988-),女,硕士,研究方向:应用数学.
O175
A
1672-0946(2015)06-0751-02
