应用三阶力梯度辛算法求解纯Kepler二体问题

李 荣

(安阳师范学院数学与统计学院，河南安阳 455000）

辛几何最早可以追溯到19世纪，英国天文学家哈密顿为了研究牛顿力学，引进了广义坐标和广义动量来表示系统的能量，称为哈密顿函数。辛几何应用于数值方法，最早出现于20世纪80年代初的文献。我国数学家冯康院士［1－2］于1984年首次提出了求解哈密顿系统的隐式辛算法，他指出:“传统的数值方法，除了极少数的例外，都不可避免的带有人为耗散性等歪曲体系特征的缺陷”。而辛算法弥补了这一缺陷，是一种具有高保真性算法。隐式辛算法主要运用正则变换的隐式生成函数从事辛算法的研究，优势在于适用范围广，它适用于几乎任何形式的哈密顿函数，但由于在计算中要使用迭代方法，而使得它的计算效率大大降低。同一时期，Ruth［3－4］建立了求解哈密顿系统需要分解为动能T部分和势能V部分的显式辛算法。考虑到显式辛算法的计算效率比隐式辛算法高，当哈密顿系统能分解时，显式辛算法是更好的选择。

力梯度显式辛算法［3］是一种独特的辛算法，它与非力梯度显式辛算法同时出现。通过力实现力梯度的计算，力梯度显式辛算法可以做到只含有正积分步长，这满足了在求解时间不可逆的方程时对正积分步长的需求［5－6］。Chin 和合作者［7－9］给出了满足算子形式对称的力梯度算法并把它扩展到四阶。本文构造了一系列算子形式不对称的三阶力梯度辛算法，并把它应用到求解纯Kepler二体问题［10－12］的轨道长半径中去，表明其具有很高的误差精度。

1 三阶力梯度显辛算法的构造

下表中，我们列举出几种满足条件的辛算法。

表1.1算子型三阶力梯度显辛算法的时间系数表

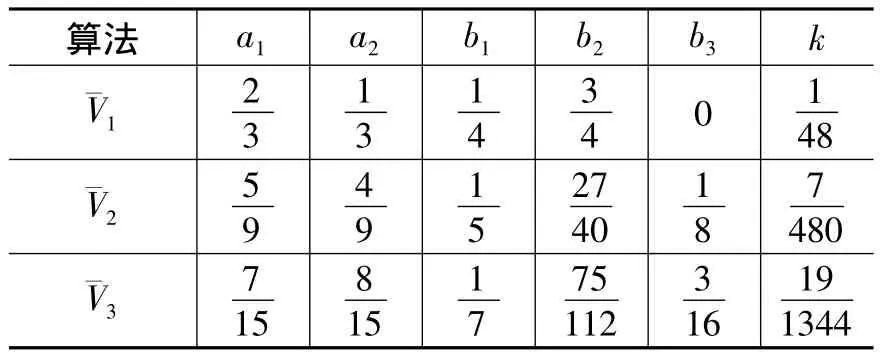
表1.1算子型三阶力梯度显辛算法的时间系数表

算法 a1 a2 b1 b2 b3 k1 23 13 14 3 4 0 1 482 59 49 15 27 40 18 7 4803 7 15 8 15 17 75 112 3 16 19 1344

表1.2 算子型三阶力梯度显辛算法得时间系数表

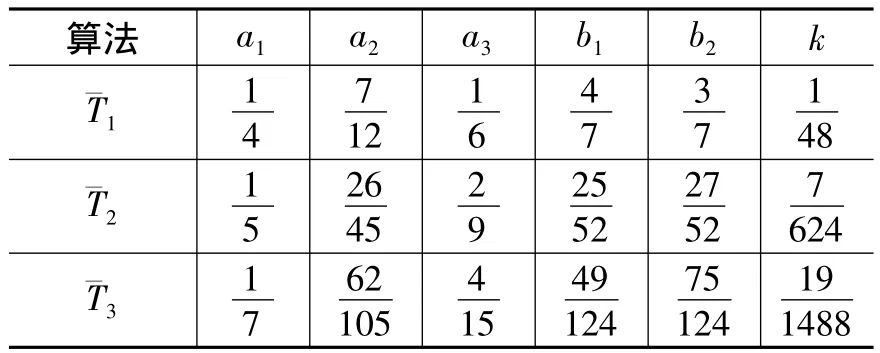
表1.2 算子型三阶力梯度显辛算法得时间系数表

算法 a1 a2 a3 b1 b2 k1 14 7 12 16 47 37 1 482 15 26 45 29 25 52 27 52 7 6243 17 62 105 4 15 49 124 75 124 19 1488

2 数值模拟

Kepler二体问题［5－6］是天体动力学中最基本的模型之一，是研究天体精确运动的理论基础，具有重要的研究意义。在零阶近似下，天体对外的引力场可被看做质量集中于质心的质点所产生的引力场，所以两天体的运动问题就可以近似视为两质点在其相互之间的万有引力作用下的动力学问题。哈密顿函数为

图2.1中，选取一条坐标和动量的初始条件分别选择 1，0，0，1的运动轨道，步长为周期的1/20。通过观察可知，每一种算法都能够很好的保持了辛算法的优势，即轨道长半径随时间周期型变化。同时，每一种算法的误差精度都能够达到10－7左右，表明这些三阶力梯度辛算法非常适用于计算天体力学中轨道参数问题。由于轨道长半径的相对误差和能量的相对误差具有正比例关系，这是因为Kepler能量E和轨道长半径a具有如下关系E－μ/2a，此处μ为引力常量。所以图2.1也可以反映系统的能量误差精度。2.1(a）、(b）、(c）图对应算子型力梯度辛算法，(d）、(e）、(f）图对应算子型力梯度辛算法。总体来说，算子型力梯度辛算法的误差精度相较于算子型要高一个数量级左右，其中以算法最优。

3 小结

在研究哈密顿系统的动力学性质时，传统的数值方法由于存在人为耗散性等歪曲体系特征导致系统能量得不到保持，这将使得数值解法产生失真。本文构造了一系列算子形式不对称的三阶力梯度辛算法，并通过求解纯Kepler二体问题的轨道长半径来验证了其有效性。

［1］Feng K.Beijing Symposium on Differential Geometry and Differential Equations［M］.Beijing:Science Press，1985.

［2］冯康，秦孟兆.Hamilton动力系统的 Hamilton算法［J］.自然科学进展 －国家重点实验室通讯［J］，1991，(2）:102 ～112.

［3］Ruth R D.A canonical integration technique［J］.IEEE Transactions on Nuclear Science，1983，NE － 30(4）:2669～2671.

［4］Forest E，Ruth R D.Fourth －order symplectic integration［J］.Phys.D，1990，43:105 ～117.

［5］Rong Li，Xin Wu.A symmetric product of two optimal third－order force gradient symplectic algorithms［J］.ACTA PHYSICA SINICA，2010，59(10），7135 ～7143.

［6］Rong Li，Xin Wu.Optimized third－order force－gradient symplectic algorithms［J］.SCIENCE CHINA，2010，53(9），1600～1609.

［7］Chin S A.Symplectic integrators from composite operator factorizations［J］.Phys.Lett.A，1997，226:344 ～348.

［8］Chin S A，Chen C R.Forward symplectic integrators for solving gravltational fewbody problems［J］.Celestial Mechanics and Dynamical Astronomy，2005，91:301 ～322.

［9］Chin S A.Physics of symplectic integrators:Perihelion advances and symplectic corrector algorithms［J］.Physical Review E，2007，75:036701

［10］刘福窑，伍歆，陆本魁.几类辛方法的数值稳定性研究［J］.天文学报，2006，47(4）:418－431.

［11］徐佳.含力梯度显辛算法拓广于摄动二体问题［J］.江西科学，2009，27(4）:506－509.

［12］Jia xu and Xin Wu.“Several fourth－order force gradient symplectic algorihhms”.Research in Astronomy and Astrophysics 2010，10(2）:173.