FitenBLAS:面向FT1000微处理器的高性能线性代数库*
2015-03-09迟利华晏益慧谢林川甘新标胡庆丰李胜国
迟利华,刘 杰,晏益慧,谢林川,甘新标,胡庆丰,蒋 杰,李胜国
(国防科技大学 并行与分布处理重点实验室,湖南 长沙 410073)
FitenBLAS:面向FT1000微处理器的高性能线性代数库*
迟利华†,刘 杰,晏益慧,谢林川,甘新标,胡庆丰,蒋 杰,李胜国
(国防科技大学 并行与分布处理重点实验室,湖南 长沙 410073)
BLAS库是基本线性代数子程序库,是许多大型科学与工程计算的核心计算程序,FitenBLAS库是在多核多线FT1000微处理器上开发的基本线性代数库,其研制对FT1000微处理器在科学与工程计算中的应用具有重要意义.根据多级存储结构和寄存器的数目,设计了向量与向量、矩阵与向量和矩阵与矩阵运算的多级循环展开方法,采用指令调度、数据预取等通用优化技术,优化BLAS库串行程序.对于BLAS3子程序,设计了矩阵乘无冗余数据拷贝分块算法,采用指令重排、访存与计算的重叠、分块等技术优化矩阵乘子程序,基于矩阵乘子程序实现了其他BLAS3子程序.研制了汇编线性代数程库FitenBLAS,其核心子程序矩阵乘的双精度计算性能达到6.91Gflops,是峰值性能的86.4%.
FT1000微处理器;BLAS库;性能优化
基本线性代数子程序BLAS(Basic Linear Algebra Subroutines)库,提供最基本的线性代数函数接口[1],分为三级:BLAS 1(Level 1)包括向量与向量操作子程序,如点积、向量相加等.BLAS 2(Level 2)包括矩阵与向量操作子程序,如矩阵向量相乘等.BLAS 3(Level 3)包括矩阵与矩阵操作子程序,如矩阵与矩阵相乘等.
BLAS库是每款微处理器要移植和优化的数学库,是许多大型科学与工程计算的核心计算模块,同时BLAS库子程序可以反映许多应用程序的计算特点,如果BLAS库可以在微处理器上获得高性能,同样的应用程序也可以获得好的性能,BLAS库程序可以验证微处理器的功能和计算性能.因此各个厂家在新型号微处理器推出时,都会配套针对微处理器特点研制、优化和推出高性能BLAS库,BLAS库已经成为微处理器的必备数学库之一.
Intel公司针对通用CPU开发了MKL基本数学运算库[2],包含采用多线程进行并行计算的函数库,可以在结点内实现高性能;AMD公司针对通用CPU开发了ACML基本数学运算库[3],具有MKL类似的特点;IBM公司开发了ESSL基本数学运算库[4].上述厂商开发的基本数学运算库,均包含了使用汇编语言手工优化的高性能BLAS库.GotoBLAS[5-6]是开源的针对不同类型的微处理器开发的BLAS库,提供了OpenMP多线程并行版本,是性能最好的BLAS库之一,2008后不再更新,不支持最新推出的微处理器;ATLAS[7-8]针对不同的微处理器提供可以自动优化的BLAS库.OpenBLAS是针对龙芯等微处理器开发的高性能BLAS库[9-10].
FT1000是由国防科学技术大学研制的单芯片多线程(CMT)处理器,是天河-1A计算结点采用的微处理器之一[11].BLAS库在FT1000上获得高性能是需要研究的重要问题,目前没有可以在FT1000上运行的高性能BLAS库,本文结合FT1000多核多线微处理器特点,设计了并行计算方法和数据结构,研制了手工汇编子程序,进行了针对性的性能优化,研制了高性能线性代数库FitenBLAS.
1 FT1000微处理器
FT1000微处理器包含8个处理器核,每核包含8套硬件现场,支持8个线程.每个线程有1个完整的寄存器文件,大部分ASI,ASR和特权寄存器都是每个线程1份.
每个核包含2条整数流水线、1条浮点流水线和1条存储流水线.8个线程共享浮点流水线和存储流水线.8个线程分成2组,每组4个线程,共享1条整数流水线.虽然8个线程同时运行,但是在任意时刻,最多两个线程是活跃的,这两个线程发射的指令只可能是下面的组合:1对整数操作、1个整数和1个浮点、1个整数和1个存储、1个浮点和1个存储.每个组内的线程按照LRU算法每个周期进行切换.
每个核内有独立的一级数据cache和一级指令cache.L1I Cache大小为 16 kB,8路组相联,块大小32字节.L1D Cache大小为8 kB,4路组相联,块大小32字节.指令TLB为64项全相联,数据TLB为128项全相联.8个线程共享L1I,L1D和TLB,通过TLB中的自动释放机制使多个线程更新TLB.
FT1000微处理器采用SPARC V9指令集,现有的BLAS线性代数库不能直接运行,需要重新设计.
2 程序优化方法
2.1 循环展开方法
循环展开可以减少循环体的循环次数,减少分支执行的时间,为流水线提供更多的并行机会,是一种通用的程序优化方法,是手工汇编优化BLAS子程序的主要方法.在循环展开中,展开因子的选择是核心问题,目前的编译器一般只对循环体很小的循环进行循环展开,且使用的展开因子是很小的常数,这可能损失一些计算性能,特别是对于多层嵌套循环,编译器的优化效果不明显,只能采用手工的循环展开优化.
BLAS 1(Level 1)包括向量与向量操作子程序,包含SUM,DOT,AXPY,COPY,SCAL等子程序.当跨步为1时,BLAS1程序中的计算操作针对一维数据进行连续访问,具有良好的空间数据局部性,可以采用手工循环展开来优化性能.采用汇编编程时寄存器的数目限制了展开次数,为此,本文根据寄存器的数目进行多级展开,展开因子可以随意调节,在展开循环体内,循环使用寄存器.以AXPY为例来说明多级展开方法,图1给出了多级展开循环体,双精度浮点寄存器的数目为n,涉及2个向量运算,平均使用向量寄存器,每个向量使用的寄存器最大数目为n/2,循环展开因子可以取为m“*”n/2.ldd,fmuld,faddd和std是汇编指令,分别表示取数、相乘、相加和存数.为了表示方便,图1中使用了循环控制变量,在实际展开的循环体中,没有循环控制变量,而将图1中的循环体重复m“*”n/2次.
AXPY使用寄存器的多级展开循环体:
浮点寄存器数目为n,令k=n/2
循环展开因子为m*k
数组a(*)和b(*)表示不同的寄存器
alpha为寄存器,保存标量值
for i ← 0 to m*k-1 step k do
for j ← 0 to k -1 do
ldd x[m*i+j], a[j];
fmuld a[j], alpha, a[j];
ldd y[m*i+j], b[j];
faddd a[j], b[j], b[j];
std b[j], y[m*i+j];
endfor
endfor
图1 BLAS1子程序AXPY多级展开循环体
Fig.1 Multi-level loop unrolling for subroutine AXPY of BLAS1
根据寄存器数目,图1中给出的是AXPY多级循环展开的一般方法,BLAS1其它子程序中可以根据图1中给出的展开方法,进行多级循换展开.针对FT1000微处理器,双精度寄存器数目为32,对于AXPY子程序,每个向量至多使用16个寄存器.使用16个寄存器时,循环展开因子就是16的倍数,同样地循环展开因子可以是12,13,14和15等数的倍数,可以根据实际测试情况,进行调整,以找到最佳的循环展开因子.
BLAS2包括矩阵与向量操作子程序,如矩阵-向量乘、rank-1和rank-2矩阵校正等,涉及二维数组A和一维数组x和y间的计算操作,计算结果为一个一维数组.以矩阵向量乘GEMV子程序为例进行说明,为了复用一维数组x,对数组x进行分段,对数组A进行分块.在分配寄存器时,二维数组A,一维数组x和y以及保存临时变量的一维数组z给分配寄存器总数的1/4.针对FT1000微处理器,双精度寄存器数目为32,对于GEMV子程序,数组A至多使用8个寄存器,一维数组x和y分别使用8个寄存器.使用8个寄存器时,循环展开因子就是8的倍数,同样地循环展开因子可以是4,5,6和7等数的倍数,可以根据实际测试情况,进行调整,以找到最佳的循环展开因子.图2给出了BLAS2子程序GEMV多级展开循环体.
GEMV使用寄存器的多级展开循环体:
浮点寄存器数目为q,令k=q/4
循环展开因子为m*k和n*k
数组M(*,*)、a(*)和b(*)表示不同的寄存器
alpha为寄存器,保存标量值
for i ← 0 to m*k-1 step k do
for j ← 0 to n*k -1step k do
for v ←0 to k-1 do
ldd x[n*j+v], a[v];
fmuld a[v], alpha, a[v];
for u ←0 to k-1 do
ldd A[m*i+u, n*j+v], M[u,v];
ldd y[m*i+u], b[u];
fmuld M[u,v], a[v], c[u];
faddd b[u], c[u], b[u];
endfor
endfor
endfor
for u ←0 to k-1 do
std b[u], y[m*i+u];
endfor
endfor
图2 BLAS2子程序GEMV多级展开循环体
Fig.2 Multi-level loop unrolling for subroutine GEMV of BLAS2
BLAS 3(Level 3)包括矩阵与矩阵操作子程序,包含GEMM,SYMM,SYRK,SYR2K,TRMM和TRSM等子程序.矩阵乘GEMM子程序是BLAS3的核心,其它BLAS3子程序可以基于GEMM来实现.下面以GEMM子程序为例来进行说明.所要求解的矩阵乘形式如下:
C=βC+αA×B
其中A∈Rm×k,B∈Rk×n,C∈Rm×n,α和β是实数.
矩阵乘在多级存储结构上获得高性能的基本方法是分块算法,将A,B和C划分成如下子矩阵:
其中Aip∈Rmc×kc,Bpj∈Rkc×nr,Cij∈Rmc×nr.
原矩阵乘算法转化为多个子矩阵相乘,根据Cache和TLB的大小来选择子矩阵的大小.具体实现时选取Aip的大小为L2Cache大小的一半,同时保证不发生TLB失效,并驻留在二级Cache中,直到不再使用为止,即完成如下操作:
计算时,子矩阵Bp,j(j=1,…,N)以流水的方式进入L1DCache.Ci,j的数据不重用,不必长时间保存在L1D和L2Cache中.
把寄存器总数的一半分配给矩阵C使用,另一半寄存器被矩阵A,矩阵B和临时变量平均使用.针对FT1000微处理器,双精度寄存器数目为32,对于GEMM子程序,数组C至多使用16个寄存器,数组A和B分别使用4个寄存器,剩下的作为临时变量寄存器使用.图3给出了BLAS3子程序GEMM按照4*4*4展开的循环体.
通过指令的合理调度、数据的预取和寄存器的合理使用,当Ai,p,Bp,j和Ci,j在Cache中时,可以发挥CPU的峰值性能.
GEMM_kernel使用寄存器的循环展开体:
浮点寄存器数目为q,令t=4
循环展开因子为m*t、n*t和k*t
数组D(*,*)、a(*)和b(*)表示不同的寄存器
for j ← 0 to n*t-1 step t do
for i ← 0 to m*t-1 step t do
for k ← 0 to q*t-1 step t do
for u ←0 to t-1 do
for v ←0 to t-1 do
for w ←0 to t-1 do
ldd A[t*i+u, t*j+w], a[w];
ldd B[t*i+w, t*j+w], b[w];
fmuld, a[w], b[w] , tmp;
faddd M[u,v], tmp, M[u,v];
endfor
endfor
endfor
endfor
endfor
endfor
图3 BLAS3子程序GEMM按照4*4*4展开循环体
Fig.3 Multi-level loop unrolling for subroutine GEMM of BLAS3
2.2 数据预取
矩阵和向量是存放于内存中的,计算过程中,通过多级存储结构,将数据取到寄存器中开始运算,数据的预取可以很好地实现数据传输和计算的重叠,是提高数据空间局部性的性能优化方法.开始执行计算时,参与运算的矩阵和向量存放在内存中,开始的取数不会命中Cache,FT1000上从内存中取数到二级Cache的延迟大于100拍(即100个CPU时钟周期),Cache块大小为32字节,每次内存访问,同时会把内存中连续的32字节分别存放到二级Cache和一级数据Cache中.
数据预取就是将后面要用的数据提前取到L2 Cache中,将访存的数据传输操作和乘加计算操作重叠起来,如果计算时间大于数据传输时间,那么整个计算就可以得到CPU的峰值性能,如矩阵相乘.通过参数可以调整数据预取的间隔,获得最佳性能.
BLAS1,BLAS2和BLAS3均用到数据预取,本文仅以双精度AXPY为例来说明数据预取方法,图4给出了带数据预取的展开循环体.
AXPY带数据预取的展开循环体:
令k=8,PREFECHSIZE=8,SIZE=8
循环展开因子为m*8
数组a(*)、b(*)和c(*)表示不同的寄存器
for i ← 0 to m*8 step 8 do
for j ← 0 to 4 do
ldd x[m*i+j], a[j];
fmuld a[j], alpha, a[j];
ldd y[m*i+j], b[j];
faddd a[j], b[j], b[j];
std b[j], y[m*i+j];
endfor
prefetch [&x[m*i]+PREFETCHSIZE * SIZE], 0
prefetch [&y[m*i]+PREFETCHSIZE * SIZE], 0
for j ← 5 to 8 do
ldd x[m*i+j], a[j];
fmuld a[j], alpha, a[j];
ldd y[m*i+j], b[j];
faddd a[j], b[j], b[j];
std b[j], y[m*i+j];
endfor
prefetch [&x[m*i+4]+PREFETCHSIZE * SIZE], 0
prefetch [&y[m*i+4]+PREFETCHSIZE * SIZE], 0
endfor
图4 BLAS1子程序AXPY带数据预取的展开循环体
Fig.4 Multi-level loop unrolling with the prefetching data for subroutine AXPY of BLAS1
FT1000通过预取指令对内存数据进行操作,SIZE表示一个数据所占的内存字节数,PREFECHSIZE表示提前预取数据间隔,可以根据需要改变大小.图4中,预取的数据提供给下一次循环体使用,将数据从内存中,取到二级Cache中,预取数的时间和图4中的两个小循环进行时间重叠,用计算重叠数据传输.
3 多线程并行计算方法
对BLAS1采用向量一维平均划分的方式组织并行计算.对BLAS2中涉及的二维矩阵采用按行或按列一维划分.对BLAS3中涉及的二维矩阵采用按行和按列二维划分.
下面重点对BLAS3中的矩阵乘并行计算方法展开讨论.
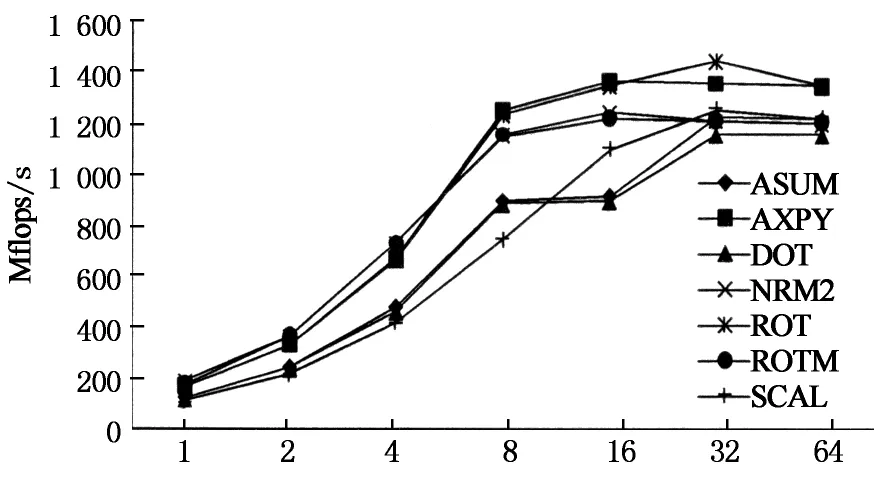
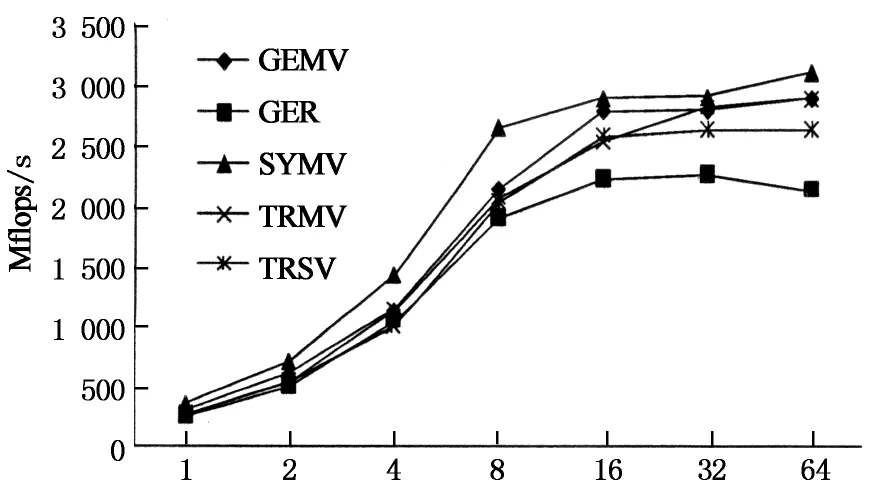
P个线程按pr×pc划分成二维拓扑结构, 满足P=pr×pc.假设P(r,c) (0≤r 多线程矩阵乘并行算法: 全局数组 局部数组 r,c, 每一个线程P(r, c),其中 ,执行: for i→r×mrto r×mr+mrdo for l←0 to k-1 do 第r行线程中的任一线程将子矩阵 拷贝到 for j←c×ncto c×nc+ncdo end for end for end for 图5 避免重复拷贝A子矩阵的多线程矩阵乘并行算法 Fig.5 Multi-thread parallel matrix multiplication algorithm avoiding the redundant packing ofA BLAS3中的SYMM,SYR2K,SYRK,TRMM和TRSM子程序并行算法均基于GEMM实现,参考文献[12]. 测试环境的硬件平台为8核FT1000微处理器,主频为1 GHz,双精度浮点性能8Gflops.操作系统为银河麒麟操作系统,编译器为gcc-4.5.1. 图6给出了BLAS1的双精度性能测试结果,固定向量的长度n不变,统一取为256 000 000.从图6可以看出,从1线程到8线程各BLAS1程序具有明显的加速效果,各程序在16或32线程时,达到最高性能,64线程时性能略有下降.造成32或64线程性能下降的主要原因是:1)BLAS1程序的计算访存比是1或2,受限于访存;2)BLAS1程序访存有空间局部性,没有时间局部性,也就是不存在数据的复用;3)FT1000微处理器的访存带宽在16或32线程时达到最大. No of threads 图7给出了BLAS2的双精度性能测试结果,固定矩阵的长度n不变,统一取为16 000.从图7可以看出,浮点性能明显高于BLAS1的性能,性能最好的SYMV在64线程时达到最高性能,3.11Gflops/s,是峰值性能的38.8%,SYMV的计算访存比是6,存在空间和时间局部性.BLAS2中的其他子程序的计算访存比是3,只有空间局部性,不存在时间局部性. No of threads BLAS3双精度浮点性能测试结果由图8给出,由于BLAS3的计算访存比大,对于阶为N的方阵,计算量为2N3,访存量为3N2,在64线程时获得最高性能,对不同的计算规模展开测试.从图8中可以看出,矩阵乘GEMM的最高性能达到6.91Gflops,是峰值性能的86.4%.SYMM,SYR2K,SYRK,TRMM和TRSM子程序的最高性能分别达到6.75,6.73,6.74,6.75和6.69Gflops,和矩阵乘GEMM的性能接近. 影响矩阵乘GEMM性能的主要因素包括:1)数据拷贝开销.为了充分发挥多级Cache的性能,采用了分块算法,分块子矩阵在内存中的存储是不连续的,为了减少对TLB冲突,需要将矩阵A和B的数据预先拷贝到一个连续的内存空间.2)数据延迟时间.每个子矩阵块相乘前,每个线程需要进行数据的填充,数据需要从内存中传输到L2 Cache,从L2 Cache到L1 Cache,从L1 Cache到寄存器,每个数据大概需要150拍,150拍过后,每拍可以取一个双精度数据.3)数据对存储带宽的竞争.64线程并行计算时,需要同时从内存中取数,数据带宽成为影响性能的因素.4)计算不能全覆盖数据的存取.FT1000微处理器中每核启动8线程,8线程共享一套硬件计算资源,靠多线程的切换来屏蔽访存延迟.这种情况主要存在每个循环展开启动阶段,8线程需要同时取数,此外循环展开计算完成后,需要把计算结果保存到矩阵C中,此时存取数据量和计算量处于相同量级. M=N=K 相对于其他X86微处理器,FT1000是多核多线体系结构,每8线程共享一个计算核,通过线程切换来屏蔽访存延迟,相对而言更难发挥其峰值性能,我们认为矩阵乘GEMM双精度能发挥峰值性能的86.4%已经是能达到的最好浮点性能. 提炼共性基础数值算法,研制高性能计算库,统一编程接口,是用户充分发挥微处理器峰值性能的重要手段.BLAS库是基础线性代数库,需要根据CPU的具体特点,设计高性能的算法和数据结构,经过高度的手工汇编优化,其中的BLAS3可得到接近峰值的浮点性能,满足用户的性能要求. 本文基于国防科学技术大学研制的多核多线FT1000微处理器,研制了基本线性代数汇编子程序库FitenBLAS,根据寄存器的数目,设计了向量与向量、矩阵与向量、矩阵与矩阵运算的多级循环展开方法,采用计算指令流水线调度、数据预取等通用优化技术,优化BLAS库串行程序.对于BLAS3子程序,设计了矩阵乘无冗余数据拷贝分块算法,采用指令重排、访存与计算的重叠、分块等技术优化矩阵乘子程序,基于矩阵乘子程序实现了其他BLAS3子程序.其核心子程序矩阵GEMM乘的双精度计算性能达到6.91Gflops,是峰值性能的86.4%. 下一步,面向短向量飞腾微处理器,研制支持向量优化运算的BLAS库,吸收并行编程框架底层调用的矩阵向量运算和稀疏线性数值算法,完善FitenBLAS库,支持更加广泛的数值模拟运算. [1] DONGARRA J. Basic linear algebra subprograms technical forum standard [J]. International Journal of High Performance Applications and Supercomputing, 2002, 16(1): 1-111. [2] Intel MKL homepage. http://software.intel.com/zh-cn/intel-mkl/ [3 AMD ACML homepage. http://developer.amd.com/cpu/ libraries/acml/ [4] IBM ESSL homepage. http://www-03.ibm.com/systems/software/essl/ [5] GotoBLAS homepage. http://www.tacc.utexas.edu/tacc-projects/gotoblas2 [6] GOTO K, VAN DE GEIJN R. Anatomy of high-performance matrix multiplication [J]. ACM Transactions on Mathematical Software, 2008, 34(3): 1-25. [7] ATLAS homepage. http://math-atlas.sourceforge.net/ [8] WHALEY R, PETITET A, DONGARRA J. Automated empirical optimizations of software and the ATLAS project [J]. Parallel Computing, 2001, 27(1): 3-35. [9] OpenBLAS homepage. http://xianyi.github.com/ OpenBLAS [10]张先轶,王茜,张云泉. OpenBLAS:龙芯3A CPU的高性能BLAS库 [J]. 软件学报, 2011, 22(zk2): 208-216. ZHANG Xian-yi, WANG Qian, ZHANG Yun-quan. OpenBLAS: a high performance BLAS library on Loongson 3A CPU [J]. Journal of Software, 2011, 22(zk2): 208-216. (In Chinese) [11]About FT1000 processor, http://www.nscc-tj.gov.cn/ resources/resource_1.asp, 2010-11-17. [12]GOTO K, VAN DE GEIJIN R. High performance implementation of the level-3 BLAS[J]. ACM Transactions on Mathematical Software, 2008, 35(1): 1-14. FitenBLAS: High Performance BLAS for a Massively Multithreaded FT1000 Processor CHI Li-hua†, LIU Jie, YAN Yi-hui, XIE Lin-chuan, GAN Xin-biao,HU Qin-feng, JIANG Jie, LI Sheng-guo (National Laboratory for Parallel and Distributed Processing, National Univ of Defense Technology,Changsha,Hunan 410073,China) BLAS library is the fundamental linear algebra library and plays an important role in many large scientific applications. This paper developed a linear algebra library named FitenBLAS on a massively multithreaded FT1000 processor. Based on the hierarchical storage system and the number of registers, multilevel loop unrolling methods were developed for vector-vector, matrix-vector and matrix-matrix linear operations. The codes of FitenBLAS were optimized with instruction layout and data prefetching technology. An avoiding redundant packing method was proposed for parallel matrix-matrix multiplication, and the parallel code was developed. The kernel matrix-matrix multiplication code was optimized with instruction layout, time overlapping of data access and computation, and data blocking. The other BLAS3 subroutines were designed on the matrix multiplication code. The kernel codes of FitenBLAS were developed in assembly language. The performance for the key subroutine of the matrix multiplication reaches 6.91Glops/s, nearly 86.4% of the peak performance of the FT1000. FT1000 Processor; BLAS; code performance optimization 1674-2974(2015)04-0100-07 2014-10-16 国家自然科学基金资助项目(60970033),National Natural Science Foundation of China(60970033) ;国家高技术研究发展计划(863计划)资助项目(2012AA01A301) 迟利华(1970-),女,山东威海人,国防科技大学副研究员,博士 †通讯联系人,E-mail:chilihua@nudt.edu.cn TP332.2 A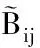
4 性能测试与分析

5 结论与展望
