非线性温度梯度作用下水泥混凝土路面力学分析*

颜可珍, 沈光辉, 游凌云

(湖南大学 土木工程学院，湖南 长沙 410082)

非线性温度梯度作用下水泥混凝土路面力学分析*

颜可珍†, 沈光辉, 游凌云

(湖南大学 土木工程学院，湖南 长沙 410082)

为合理评价水泥路面温度沿深度方向的非均匀性分布对水泥混凝土板的应力和变形的影响，利用有限元软件模拟非线性温度梯度荷载；为分析不同程度非线性温度梯度对板的应力响应引入了非线性温度分布指数.研究结果表明：以线性温度梯度计算非线性温度梯度应力时，正温度梯度的应力偏大，负温度梯度的应力偏小.非线性温度梯度时板的变形和线性温度梯度板产生的变形则基本相同.负非线性温度梯度分布时：随着板厚和板弹性模量的增加，非线性温度梯度对板顶的应力影响增大；增加地基反应模量可以减小非线性温度梯度影响.并通过大量数据回归分析得出负温度梯度时板顶下最大应力计算公式.

水泥混凝土路面；非线性温度梯度；非线性温度分布指数；温度应力

Westergaard采用Winkler 地基推导出水泥混凝土路面温度翘曲应力公式[1]，之后的研究者大多假设温度梯度沿板厚呈线性分布[2].而Teller的研究表明水泥混凝土面板深度范围内的温度场分布事实上是高度非线性的[3]，Choubane通过大量的分析实测数据证明非线性温度沿着板厚的分布可以很好地拟合为二次多项式[4]，国内的温度场的研究也证明了水泥路面温度场分布的非线性[5-6].已有的研究结果表明忽视了温度梯度的非线性分布, 计算结果显然与实际路面的温度应力值不符[6-8].现行规范《公路水泥混凝土路面设计规范》[9](JTGD40—2011)在计算路面板温度应力时，考虑了温度非线性分布引起的内应力，并给出了综合温度翘曲应力和内应力的修正系数计算公式，但以正温度梯度为主，并未考虑正负非线性温度梯度对路面板应力影响的区别.Hiller的研究表明以线性温度梯度计算非线性温度应力的影响时，正温度梯度时应力结果偏大，负温度梯度时应力偏小[10].而且正温度梯度时最大温度应力出现在板底，负温度梯度时最大温度应力出现在板顶， 田波的研究中提到，板内负温度梯度引起的板顶拉应力值也很大，与不利荷位组合时将引起板的top-down开裂[5]，负温度时非线性温度梯度对板应力的影响同样不能忽略[11].此外此前的研究大多以一天内不同时刻的温度分布作为非线性温度荷载，对不同程度非线性温度梯度的研究则较少.因此对不同程度非线性温度梯度对板的应力响应进一步分析仍有积极意义，负温度梯度时尤为重要.

基于此，本文通过有限元软件Everfe2.25模拟温度梯度沿板厚的非线性分布，分析非线性温度梯度应力和变形的影响以及不同程度非线性温度梯度对板应力的影响.引入了非线性温度分布指数的概念，在此基础上分析负非线性温度梯度时，不同参数对板顶应力的影响规律和板顶最大应力计算公式.

1 有限元模型建立

1.1 EverFe软件简介

Everfe是由美国华盛顿大学开发，用于模拟有接缝的水泥混凝土路面(PJCP)在轮载及温度作用下的力学响应.软件可以沿板厚定义线性温度梯度、双阶线性温度梯度、三阶线性温度梯度，根据温度变化及用户输入的温度膨胀系数，模拟温度的影响和收缩.本文采用三阶线性温度梯度模拟板的非线性温度梯度，如图1所示.

图1 三阶线性温度梯度

1.2 有限元模型建立和基本假设

本文采用Winkler地基单块板模型，不计板的自重.不考虑基层影响，水泥路面板直接置于地基之上，面板四边均自由，板尺寸为5 m×5 m，如图2所示.

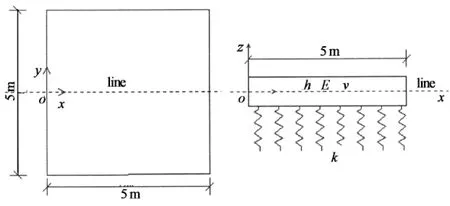
图2 模型示意图

本文所选单块板模型，面板、基层和底基层均被视为3维、线弹性、各向同性并且连续.温度只沿路面厚度方向变化，等深度下路面内部任一位置温度值相同.混凝土温度收缩系数不随温度变化，混凝土线膨胀系数取α=1.0×10-5/℃.路面结构层参数如表1所示.

表1 路面各结构层参数

2 非线性温度梯度对板应力变形影响

2.1 温度场分布规律

根据胡昌斌等在福州所测温度场数据，不同时刻路面内部温度沿深度分布如图3所示[6].

图3 不同时刻路面温度随深度变化曲线

从图3可看出温度沿着路面板厚度方向呈非线性分布，随着路面深度的增加，温度的变化趋势越来越小，路面达到一定深度后，路面内部温度基本保持不变.本文选1∶00的温度荷载为负非线性温度荷载，13∶00的温度荷载为正非线性温度梯度荷载.

2.2 非线性温度梯度对板应力的影响

H= 24 cm，E= 30 000 MPa，K= 0.05 MPa/mm时，分别计算1∶00和13∶00时考虑非线性温度影响和不考虑非线性温度影响板中X方向应力沿板厚度范围内的变化情况如图4，规定拉应力为正.

应力/MPa(a)负温度梯度

应力/MPa(b)正温度梯度

由图4(a)可知，负温度梯度时，非线性温度梯度时板底压应力相较与线性时有所减小甚至由压应力变为拉应力，板中一段的压应力相比线性有所增加，板顶拉应力则明显增加，从0.610 MPa增加到0.911 MPa，增加了49.34%.板最大拉应力出现在板顶.

由图4(b)可知,正温度梯度时，非线性温度梯度时板底拉应力相较与线性时减小，由2.446 MPa减小到0.724 MPa，减小了70.40%.板中一段的拉应力相比线性有所增加，最大拉应力出现在板中靠近板底侧，且小于线性温度梯度时板底的最大拉应力.板顶压应力则明显增加.

2.3 非线性温度梯度对板变形的影响

路面板参数不变，取板长边中线(如图2所示虚线line)为研究对象，分别计算距板边不同距离(板竖向中点)处的板的竖向位移如图5所示，规定板向上位移为正.

距板边距离/m(a)负温度梯度

距板边距离/m(b)正温度梯度

负温度梯度时板变形如图5(a)，板两边向上翘曲，板中向下翘曲，水泥混凝土板的变形沿着板中对称成凹字形.正温度梯度板变形如图5(b)，板两边向下翘曲,板中向上翘曲，水泥混凝土板的变形沿着板中对称成凸字形.非线性温度梯度作用下板的变形曲线和线性温度梯度作用时板的变形曲线基本重合.

从以上分析结果可以得出，以线性温度梯度计算非线性温度梯度应力时，正温度梯度时结果偏大负温度梯度时应力偏小.以本文所选温度场为例，虽然正温度梯度远大于负温度，考虑非线性温度分布影响时，二者所引起的板的最大应力并无太大差别.非线性温度梯度时板的变形和线性温度梯度板产生的变形则基本相同.

3 不同程度负温度梯度对板应力影响

3.1 4组负温度梯度的分布

为进一步研究负非线温度梯度对板的应力的影响，选取板温度差相同的4组温度梯度分布情况如图6所示，从case1到case4非线性越来越明显.4组温度梯度可以由式(1)表示，其中case1为线性温度梯度，其余3组为非线性温度梯度，参数见表2.

(1)

其中z为路面深度；a，b，c为相关回归系数.

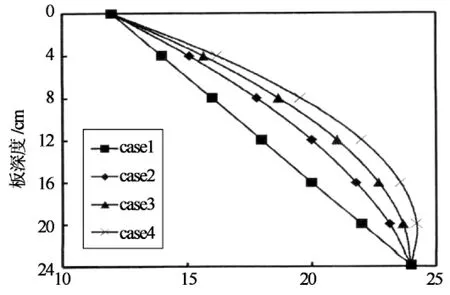
温度/℃

表2 4种温度梯度表达式的参数

3.2 负非线性温度对板应力的影响

模型其他参数不变，选取板长方向的中线(如图2示虚线line)为研究对像，4种温度梯度分布情况下，板顶X方向的应力随距板边的变化如图7(a)所示，板底应力变化如图7(b)所示.

距板边距离/m(a) 顶板

距板边距离/m(b) 板底

由图7可知，当温度梯度为线性温度梯度时，距板边距离相同时，板顶和板底的温度应力相同，在板中达到最大值(板顶为拉应力，板底为压应力).由图7(a)知，随着非线性分布程度的增加，板顶的拉应力增加.线性梯度时板顶中点应力为1.780 MPa，3种不同程度非线性温度相对应的应力分别为：2.222 MPa,2.447 MPa,2.667 MPa.相比较于线性温度梯度时分别增加了24.8%,37.4%,49.8%.由图7(b)知，随着非线性分布程度的增加，板底的压应力减小，部分位置由压应力变为拉应力.

由以上分析结果可知，板的温度差相同时，不同程度负非线性温度分布对板应力的影响较大，且板的最大应力出现在板顶中点，设计和分析时必须予以考虑.

3.3 非线性温度分布指数和验证

Hiller提出了非线性温度影响区域(NOLA)的概念，见式(2)，研究结果表明通过NOLA计算板的应力和实际情况较为接近[10].为近一步研究不同程度非线性温度梯度对板应力的影响，本文在前者的研究基础上提出线性温度影响区域LA，和非线性温度梯度分布指数Rn，见式(3)和(4).线性影响区域和非线性影响区域如图8所示.

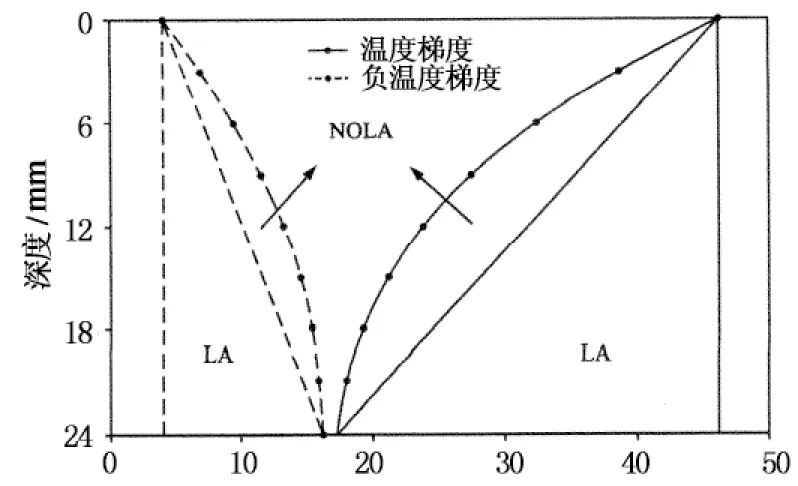
温度/℃

(1)

(2)

(3)

为验证Rn提出的合理性其他参数不变，选取板厚24cm，温度梯度ΔT=0.5 ℃.Rn相同时，不同温度梯度分布，板顶中点应力的变化如表3.

表3 相同Rn下板顶最大拉应力

注：当Rn=0时σ=1.780MPa，σ1,σ2,σ3,σ4为相同Rn下不同温度分布下对应的板顶最大拉应力.

从表3的计算结果可知，当Rn相同时，不同的温度场分布对板顶最大拉应力的影响最大不超过5%，基本可以忽略不计，故Rn可以较好地表征非线性温度梯度对板顶拉应力的影响规律.当Rn从0增大到0.4时，板顶最大拉应力从1.780MPa增加到2.674MPa，增大了49.8%,Rn与最大拉应力呈明显的单调关系.

4 参数敏感性分析

分析表明，板自重、板宽对温度应力的影响很小，通常不到0.5%，可忽略不计[12].影响路面板温度翘曲应力的主要因素有E，h，K，Δt等.为分析各因素在负非线性温度梯度对板顶中点拉应力的影响，引入任意Rn下板顶最大拉应力σRn和Rn=0即线性温度分布时板顶最大拉应力σ0的比值σRn/σ0.

4.1 板弹性模量的影响

h=24 cm，K= 0.03 MPa/mm，ΔT=0.4 ℃/cm时，E从25 000 MPa增加到40 000 MPa时，不同E对板顶最大拉应力的影响结果如图9所示.

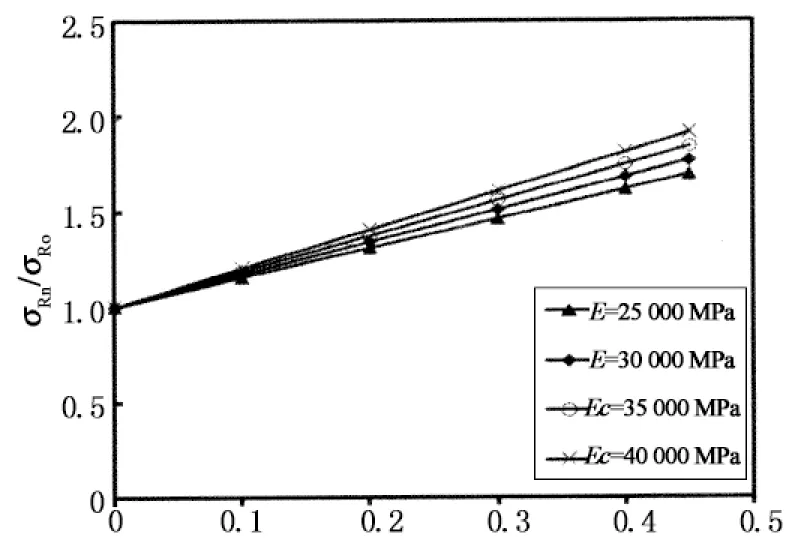
非线性温度分布指数Rn

从图中可以看出，当E为固定值时，板顶中点最大拉应力基于Rn正线性相关.随着E的增加，相同Rn下σRn/σ0的增加较为明显.即板弹性模量增加，非线性温度梯度对板顶最大拉应力的影响增大.

4.2 地基反应模量的变化

h= 24 cm，E= 30 000 MPa，ΔT=0.4 ℃/cm时，K从0.02 MPa/mm变化到0.20 MPa/mm，K对板顶最大拉应力的影响结果如图10.

非线性温度分布指数Rn

当K为固定值时，板顶中点最大拉应力基于Rn正线性相关.随着K的增加，相同Rn作用下板σRn/σ0减小；当K大于0.10 MPa/mm时，σRn/σ0的值则无明显变化.即随着地基反应模量的增加，非线性温度分布对板顶最大拉应力的影响减小，当K大于某一临界值K0时，增加地基反应模量，非线性温度分布对板顶最大拉应力的影响则不再变化.蒋应军的研究表明临界值K0与板厚度有关[12].

4.3 板厚度的影响

E=30 000 MPa,ΔT=0.4 ℃/cm,K=0.03 MPa/mm,h从18 cm增加到27 cm，不同h对板顶最大拉应力的影响结果如图11所示.

非线性温度分布指数Rn

从图中可以看出，当h为固定值时，板顶中点最大拉应力基于Rn正线性相关.随着h增加，相同Rn下的σRn/σ0增加较为明显.即板厚增加，非线性温度梯度对板顶最大拉应力的影响增大.

4.4 温度梯度的影响

h=24 cm，E=30 000 MPa，K=0.03 MPa/mm时，ΔT从0.4 ℃/cm变化到0.8 ℃/cm，ΔT对板顶拉应力的影响结果如图12所示.

非线性温度分布指数Rn

从图12中可以看出几种温度梯度作用下σRn/σ0几乎完全重合.在考虑非线性温度梯度对板的应力影响时，Rn相同时各温度梯度对板拉应力的影响基本相同.

5 负非线性温度应力拟合计算式

根据上述参数影响分析，非线性温度应力受E，K，h，以及Rn影响较大.本文板尺寸选为5m×5m，ΔT=0.4 ℃/cm，其它参数范围为：E=25 000～40 000 MPa，h=18～30 cm；K=0.01～0.1 MPa/mm，Rn=0～0.45.在以上参数范围内取值排列组合计算得出的384组板顶温度应力数据，并进行回归分析，得出负温度梯度时单层板板顶最大温度应力计算式(5)：

σRn=1.002σ0+4.50810-5×E+

0.019h+0.028/k-5.027Rnσ0

(5)

为了验证温式(5)的可靠性及精度问题，将本文公式计算结果值和文献[11]中温度应力值作对比，结果详见表4.文献[11]中E=27 500 MPa，K= 0.054 3 MPa/mm，h= 25.4 cm.分别按本文公式和文献[11]求解板顶最大拉应力结果见表4.

表4 不同方法计算温度应力

由表4结果可知，公式(5)的计算结果基本上接近于文献[11]值，误差不超17%，精度能满足工程计算的需要.

6 结 论

1)本文通过实测温度场数据，选择典型的正负非线性温度荷载，分析非线性温度分布对板应力和变形的影响.研究结果表明：以线性温度梯度计算非线性温度梯度应力时，正温度梯度时结果偏大负温度梯度时应力偏小；非线性温度梯度时板的变形和线性温度梯度板产生的变形则基本相同.

2)分析了负温度梯度时不同程度非线性温度梯度分布对板的温度应力影响.发现随着非线性分布程度的增加，板顶的拉应力增加，板底的压应力减小.

3)引入非线性温度分布指数概念，模拟分析不同程度的非线性温度梯度分布.研究表明负非线性温度分布时，随着板厚和板弹性模量的增加，非线性温度梯度对板顶的应力影响增大；增加地基刚度可以减小非线性温度梯度影响.并拟合出负非线性温度情况下板顶最大拉应力计算公式.

4)本文仅研究了尺寸为5 m×5 m单层板时非线性温度应力变化规律.需要进一步研究不同面板尺寸与结构组合的非线性温度应力变化规律以及车辆荷载和温度荷载共同作用时混凝土板的应力响应规律，建立考虑多因素的回归公式.

[1] WESTERGAARD H M. Analysis of stresses in concrete pavements due to variations of temperature [C]// Proceedings of the Highway Research Board 6. Washington D C: Highway Research Board,1927:201-215.

[2] 谈至明,姚祖康, 刘伯莹. 双层水泥混凝土路面板的温度应力[J]. 中国公路学报, 2003, 16(2): 10-12.

TAN Zhi-ming, YAO Zu-kang, LIU Bo-ying .Thermal stress analysis of two-layered concrete slabs [J]. China Journal of Highway and Transport, 2003, 16(2): 10-12. ( In Chinese)

[3] TELLER L W, SUTHERLAND E C. The structural design of concrete pavements, Part 2: Observed effects of variations in temperature and moisture on the size, shape and stress resistance of concrete pavement slabs[J]．Public Roads,1935, 15(9):169-197.

[4] CHOUBANE B, TIA M. Analysis and verification of thermal-gradient effects on concrete pavement [J]. Journal of Transportation Engineering, 1995, 121(1): 75-81.

[5] 田波,权磊, 牛开民. 不同基层类型水泥混凝土路面温度翘曲结构试验与理论分析[J]. 中国公路学报, 2014, 27(6): 17-26.

TIAN Bo, QUAN Lei, NIU Kai-ming.Structural experiment and theoretical analysis of thermal curling in JPCP with different base types [J]. China Journal of Highway and Transport, 2014, 27(6): 17-26. (In Chinese)

[6] 涂慕溪,林国仁,胡昌斌.福建省公路水泥混凝土路面[M]. 北京:人民交通出版社, 2010:82-84.

TU Mu-xi, LIN Guo-ren, HU Chang-bin.Joint plain concrete pavement in Fujian province [M].Beijing: China Communications Press,2010: 82-84. ( In Chinese )

[7] 谈至明,姚祖康. 非线性温度场下的水泥混凝土路面温度应力[J]. 中国公路学报, 1993, 6(4):9-17.

TAN Zhi-ming,YAO Zu-kang. Thermal stress in cement concrete pavements with non-linear temperature regime[J].China Journal of Highway and Transport, 1993, 6(4):9-17. (In Chinese)

[8] 李嘉, 朱伟平, 黄新颜. 非均布温度条件下 CRCP+ AC 复合式路面温度应力分析[J]. 湖南大学学报: 自然科学版, 2009, 36(10): 13-18.

LI Jia, ZHU Wei-ping , HUANG Xin-yan . Thermal stress analysis of CRCP+AC composite pavement under non- uniform temperature distribution[J]. Journal of Hunan University: Natural Sciences, 2009,36(10): 13-18. (In Chinese)

[9] 中华人民共和国交通部.JTGD40—2011 公路水泥混凝土路面设计规范[S].北京:人民交通出版社, 2011：40-43.

The People's Republic of China Ministry of Communications.JTGD40—2011 Specifications of cement concrete pavement design for highways [S].Beijing: China Communications Press, 2011：40-43. (In Chinese)

[10]HILLER J E, ROESLER J R. Simplified nonlinear temperature curling analysis for jointed concrete pavements[J].Journal of Transportation Engineering, 2009, 136(7): 654-663.

[11]ZOKAEI-ASHTIANI M A, TIRADO C, CARRASCO C,etal. Modeling of sab-fundation fiction in jinted cncrete pvements uder nlinear termal gadient or taffic lads[J]. Transportation Research Record: Journal of the Transportation Research Board, 2013, 2367(1): 123-131.

[12]蒋应军, 戴经梁. 刚性路面中关于温度应力计算问题[J]. 岩土工程学报, 2007, 29(6): 837-842.

JIANG Ying-jun, DAI Jing-liang.Computation of thermal stresses in rigid pavement[J]． Chinese Journal of Geotechnical Engineering, 2007, 29(6): 837-842. (In Chinese)

Mechanical Analysis of Cement Concrete Pavement on Nonlinear Temperature Profile

YAN Ke-zhen†, SHEN Guang-hui, YOU Ling-yun

(College of Civil Engineering, Hunan Univ, Changsha, Hunan 410082, China )

To evaluate the deformation and stress distribution of cement-concrete pavement under no-uniform temperature distribution along the depth direction, finite element analysis method was used in this research to simulate nonlinear temperature gradient load， and the nonlinear temperature distribution index was adopted to represent the degree of nonlinear distribution and to evaluate its effect on stress distribution. Models with different nonlinear temperature index parameters were constructed. The results indicate that, although the deformation caused by linear temperature gradient models was almost identical with that from nonlinear temperature gradient models, the linear temperature gradient models have overestimated bottom-up stresses and underestimated top-down stresses. When the nonlinear temperature gradient is negative, the influence of nonlinear temperature gradient on slab stress increases with the increase of slab thickness and elastic modulus. Besides, the effect of nonlinear temperature gradient is reduced with the increase of the base reaction module. What is more, based on the regression analysis of a large database, the formula of maximum tensile stress of the slab top was obtained.

cement-concrete slab; nonlinear temperature gradient; nonlinear temperature distribution index; temperature stress

1674-2974(2015)07-0074-07

2014-10-07

国家自然科学基金资助项目(51278188，50808077), National Natural Science Foundation of China(51278188，50808077)；湖南大学"青年教师成长计划"资助项目；湖南省普通高校青年骨干教师培养计划资助项目

颜可珍(1975-)，男，湖南桃江人，湖南大学教授，博士

†通讯联系人，E-mail: yankz2004@163.com

U411

A