不同交通方式的道路利用效率测度方法

蒋 芃，贾晓峰，柏章明

(天津市公用事业设计研究所天津300100)

0 引言

城市交通问题中，道路交通拥堵问题最为突出，其根本原因之一是交通量与道路面积之间的矛盾[1-3]。不同交通方式的运载量、道路占用面积、运行速度等不同，因此道路利用效率也各异，若采用道路利用效率高的交通方式，则完成相同运输量所占用的道路面积和时间更少，可降低道路交通拥堵程度。因此，如何科学、全面地评价各种交通方式、不同交通状态下的道路利用效率，便成为缓解交通拥堵问题的基础工作。

目前城市交通规划、管理中的综合评价[2-6]，多是从宏观角度对规划管理方案进行考评；偏重于以机动车效率为主、以道路通行能力为追求目标，对其他交通影响因素考虑不足。在理论研究方面，已有道路利用效率测度分析[1-3,5-6]多聚焦于宏观政策或具体道路，有关公共交通效率的研究[4-5,7-8]也多为宏观、定性评价为主，均不涉及具体交通方式运输过程或不同状态的道路利用效率测度方法。虽然业内公认公共交通运输效率高、小汽车运输效率低，但如何从微观角度对不同交通方式的道路利用效率进行定量测度、评价，尚没有成熟、公认的方法。城市道路交通中，客运交通量占主要部分且出行方式复杂，是造成道路交通拥堵的主要原因，本文从城市道路客运交通的运输效果与运输过程占用道路面积的需求关系入手，建立一种适用于不同交通方式的道路利用效率定量分析方法，并以天津市为例进行道路利用效率计算。

1 道路利用效率基本测度方法

交通运输的目的是将一定量人(或物体)，从出发地运送至目的地。在这一过程中需要占用道路资源，若选用的交通方式运载量越大、速度越快、运输时间越短，则运输同样人(或物体)所占用道路的时间和面积越少，即道路利用效率高，而道路利用效率越高，则越不易造成道路拥堵。

对不同客运交通方式的道路利用效率计算方法定义如下：

1）某交通方式的客运周转量

式中：F为客运周转量/(人∙m)；M 为某交通方式在运输过程中的有效载客量/人，出租汽车驾驶人不记为有效载客量；L为有效运输距离/m，即将载客量M从出发地运输至目的地的最短可行距离(绕行距离属于无效运输距离，不计入)。

2）某交通方式在完成客运周转量F的过程中所占用的道路面积

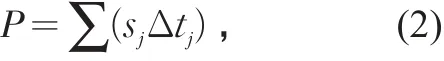
式中：P为道路占用面积/(m2·s)；sj为某交通方式在行驶状态 j时刻的道路占用面积/m2，不同交通方式的sj各异，且随速度v的不同而不同，一般表示为s(v)；Δtj为sj状态下的行驶时间/s。

3）将某交通方式在单位时间使用单位道路面积所完成的客运周转量定义为该交通方式的道路利用效率 η1/((人·m)·(m2·s)-1)：

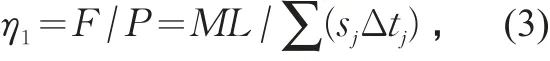
sj不变时(如车辆匀速行驶)，

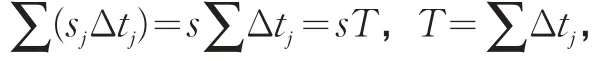
则有

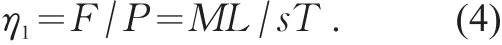
对于一个交通瞬间状态，可认为sj不变，此时该交通方式的道路利用效率

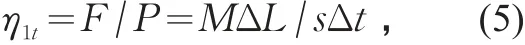
因为ΔL∕Δt=v，所以有

式中：v为瞬间状态的行驶速度/(m·s-1)；s为某交通方式在行驶状态v时的道路占用面积/m2。

例如，某自行车(载客量为1人)以11km·h-1(3.06 m·s-1)的速度行驶时，其最小安全车头间距为6 m，最小安全侧距为1.3 m(含车宽)，此时自行车的道路占用面积s=6×1.3=7.8 m2，此状态自行车的道路利用效率ηt=Mv ∕s=(1×3.06)/7.8=0.39(人·m)·(m2·s)-1。

一般情况，某交通方式在行驶状态 j时刻的道路占用面积

式中：hj为某交通方式在行驶状态 j时的最小安全车头间距/m；aj为某交通方式在行驶状态 j时的最小安全侧距/m。一般地，h和a随行驶速度v改变，有h=h(v)和a=a(v)，则

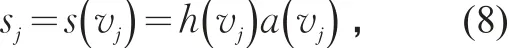
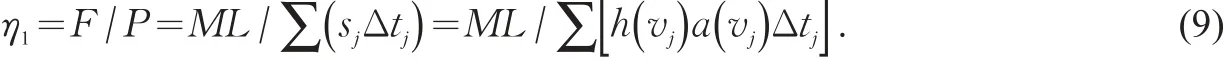
若某一交通方式的行驶过程连续，且行驶速度v可以表示为时间t的函数，即v=v(t) ，则h(v)，a(v)可表示为h(v)=h(t)，a(v)=a(t)，则s(v)=s(t)=h(t) a(t)。因此，连续行驶过程的道路利用效率

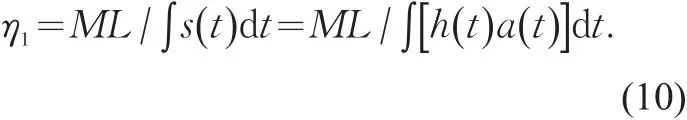
2 多方式出行道路利用效率测度方法

上述道路利用效率测度方法是针对单一出行方式进行计算，而实际中经常出现多方式出行的情况。例如公共交通出行，往往是步行与乘坐公共交通的组合过程，由于步行“载客量”为1人，而公共交通的载客量是多人，因此不能直接采用上述道路利用效率计算公式。根据道路利用效率的基本思想和式(3)，多方式出行的道路利用效率计算方法为

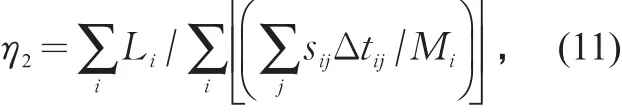
式中：η2为多方式出行的道路利用效率/((人·m)·(m2·s)-1)； Li为交通方式 i的有效运输距离/m；sij为交通方式i在行驶状态j时刻的道路占用面积/m2；Δtij为交通方式i在行驶状态 j下的行驶时间/s；Mi为交通方式i的有效载客量/人。

以“步行+公交”为例说明其道路利用效率的计算方法。该出行过程可分解为步行过程(含换乘步行)、等车过程(含换乘等车)和乘车过程；其中乘车过程还可分解为行驶过程和停车过程。因此其道路利用效率

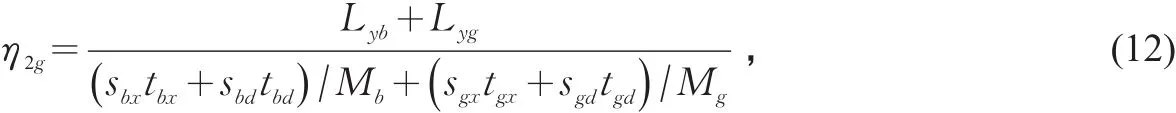
式中：Lyb为步行有效距离/m，Lyb=平均接驳距离×2×寻站接驳距离的有效系数+平均换乘接驳距离×(平均换乘系数-1)×换乘接驳距离的有效系数；Lyg为乘坐公交的有效运距/m，Lyg=公交乘行距离×乘行距离有效系数；sbx，sbd分别为步行和等车时的瞬间状态道路占用面积/m2；tbx，tbd分别为步行时间/s和等车时间/s，tbx=[平均接驳距离×2+换乘接驳距离×(换乘次数-1)]/步行速度，tbd=平均等车时间×平均换乘系数；Mb为步行载客量/人；sgx，sgd分别为公交行驶和停车状态下的瞬间状态道路占用面积/m2；tgx，tgd分别为公交行驶时间/s和停车时间/s，乘车过程道路占用总面积为Mg为公交平均载客量/人。

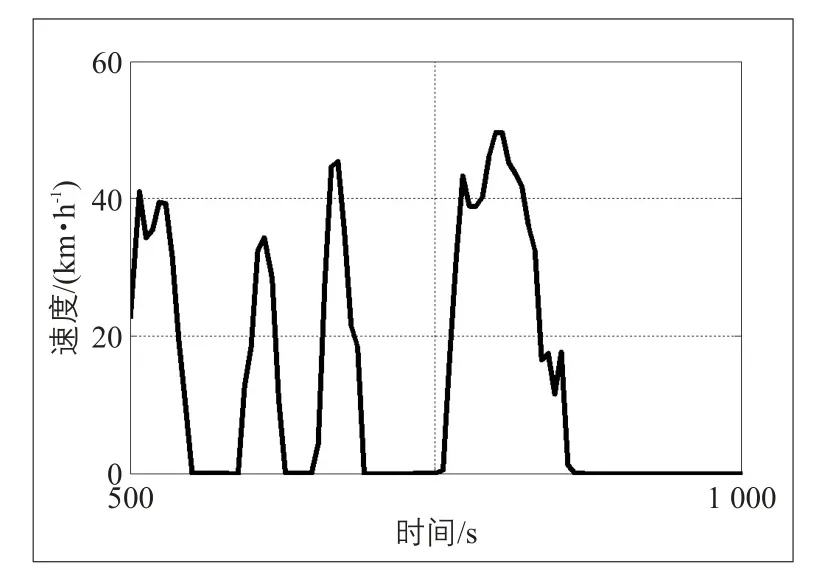
图1 小汽车行驶过程速度—时间曲线Fig.1 Speed-time curve of traveling cars

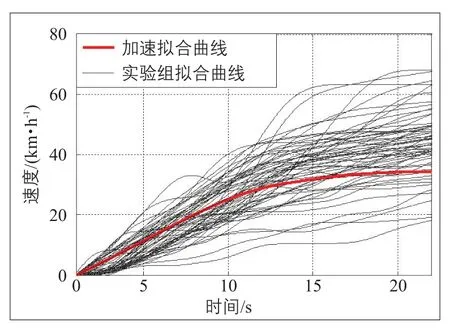
图2 小汽车加速过程路谱曲线Fig.2 Spectrum curve of acceleration process of cars

上述各变量可通过公交出行调查和公交行驶调查得到。

3 应用分析

以天津市区道路为例，应用上述方法对不同客运交通方式的道路利用效率进行测度。首先，为各采样用的车辆安装GPS和行车记录仪，使采样车辆的位置、车速等信息以1次∙s-1的频率发送至数据库服务器。车辆行驶数据采自2013年1—5月，其中小汽车行驶调查的抽样率为2‰，公交行驶调查抽样率为0.5%，电动车、自行车行驶调查抽样率为1‰。经统计分析得到不同交通方式的道路行驶规律，简称为该交通方式的“路谱”。

3.1 小汽车道路利用效率

借助采样车辆的GPS，得到小汽车在天津市外环区域内6:30—21:00的行驶数据，其行驶的速度—时间分布见图1。可以看出，小汽车在市区内呈现脉动式行驶特性，其脉动行驶过程分为4个部分：加速、稳速、减速和停车过程。基于脉动行驶过程的统计分析，得到小汽车在市区内脉动行驶的平均周期为129 s：其中行驶时间71 s，停车时间58 s，脉动周期的平均行驶距离为526 m。

本文将小汽车脉动行驶的平均周期规律称为小汽车行驶路谱。在小汽车行驶路谱中，加速过程的平均时间为22 s，拟合函数(见图2)

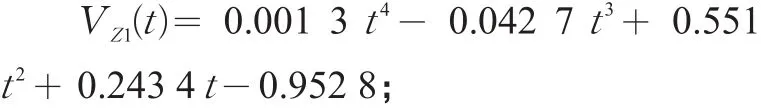
行驶路谱中平稳行驶过程的平均时间为24 s，近似匀速过程拟合函数(见图3)

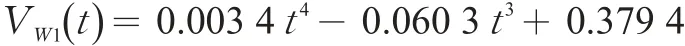
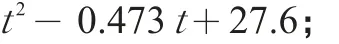
路谱中减速行驶过程的平均时间为25 s，减速过程拟合函数(见图4)

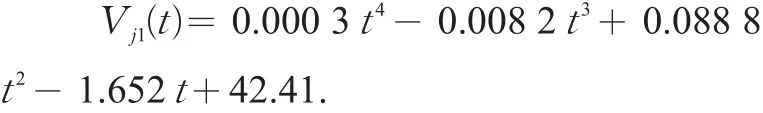
综合上述分析，得到天津市区小汽车行驶平均一个路谱周期的拟合曲线(见图5)，即路谱函数。路谱函数为计算小汽车行驶过程的道路占用面积提供依据，若按小汽车行驶时的最小安全车头时距ta=2s、小汽车平均车长4.5 m计算，则安全车头间距hx=2V(t)+4.5；市区行驶的小汽车受车道标线约束，小汽车的安全侧距ax取车道宽度(3.75 m)。由此得到小汽车行驶过程瞬间状态的道路占用面积

小汽车行驶一个路谱距离(526 m)的道路占用面积 pxlp为行驶过程与停车过程的道路占用面积之和，行驶过程是加速、稳速、减速过程之和，因此使用行驶路谱函数VZ1(t)，VW1(t)，Vj1(t)替代V(t)。则一个路谱周期中小汽车行驶过程道路占用面积

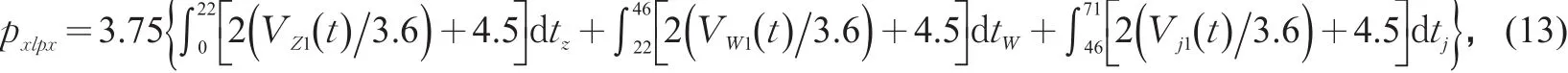
将VZ1(t)，VW1(t)，Vj1(t)函数式代入式(13)，计算得到 pxlpx=5 144m2·s。同时在一个路谱周期中，小汽车停车状态为58 s，根据调查，小汽车停车状态的平均车头间距ht=5.3m，侧距at=3.75m，则小汽车停车状态道路占用面积 pxlpt=htatt=1 153m2·s。由此得到小汽车一个路谱周期的道路占用总面积 pxlp=pxlpx+pxlpt=6 297m2·s。

通过抽样调查，得到天津市区内小汽车平均载客量为1.3人·辆-1，因此一个路谱周期的客运周转量Fxlp=ML=1.3×526=683.8人·m。

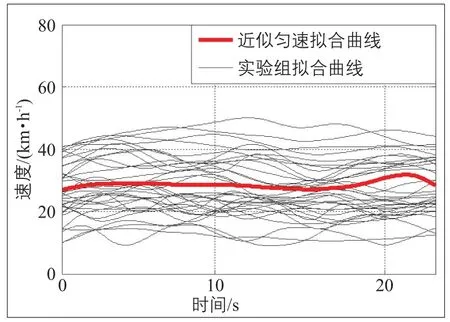
图3 小汽车近似匀速过程路谱曲线Fig.3 Spectrum curve of cars traveling in a constant speed

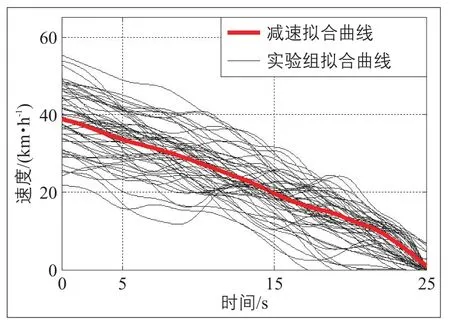
图4 小汽车减速过程路谱曲线Fig.4 Spectrum curve of deceleration process of cars

由公式(3)得到小汽车的道路利用效率

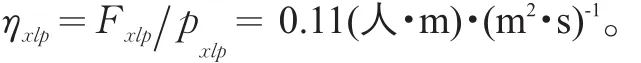
由于小汽车在城市道路按路谱周期脉动行驶，无论行驶距离多少，均为路谱距离的倍数，因此小汽车不同出行距离的道路利用效率与其路谱道路利用效率相同。由此得到天津市区内小汽车道路利用效率为0.11(人·m)·(m2·s)-1。

3.2 “步行公交”道路利用效率

通过调查得到天津市“步行+公交”出行的有关参数：平均接驳距离为340 m，寻站接驳与换乘接驳距离的有效系数均为0.7，平均换乘接驳距离为80 m，平均换乘系数为1.4，单次公交乘行平均距离为4 950 m，公交乘行有效系数为0.78，平均载客量Mg=33人。得到

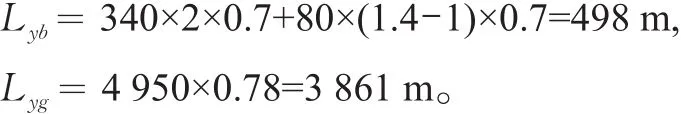
对天津市部分公交线路车辆的GPS数据进行分析，得到公交行驶路谱函数(见图6)。行驶一个路谱周期的平均行驶距离为322 m，周期为106 s。其中，加速过程平均时间20 s、稳速行驶过程26 s、减速行驶过程16 s，停车过程平均时间44 s。公交加速行驶过程拟合函数

公交平稳行驶过程拟合函数

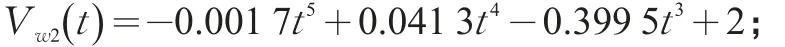
公交行驶过程减速拟合函数j2

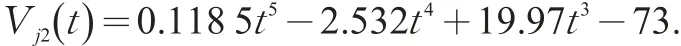
按公共汽车行驶时最小安全车头时距ta=3s，公交车辆平均车长10 m计算，得到公交安全车头间距hgx=3v(t)+10；公交安全侧距agx取车道宽度(3.75 m)。由此得到公交行驶过程瞬间状态道路占用面积则一个周期中公交行驶过程道路占用面积

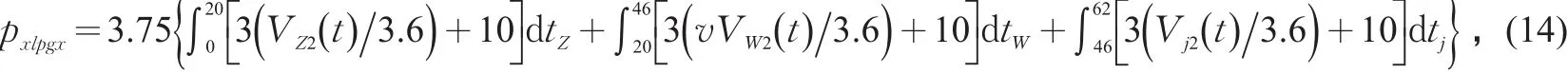
经调查得到，步行平均速度为4.3 km·h-1(1.2m·s-1)，此步行速度下行人前后的平均安全距离为2.6 m、安全侧距为1 m，因此步行瞬间状态的道路占用面积sbx=2.6m2；乘客等车状态(最低舒适)的道路占用面积sbd=0.66 m2；步行时间 tbx=[340×2+80×(1.4-1)]/1.2=593 s；平均等车时间为8.9 min(534 s)，因此 tbd=534×1.4=748 s。

将上述各值代入式(12)，得到“步行+公交”道路利用效率

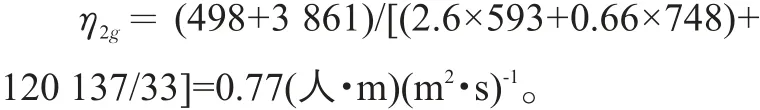
3.3 小结

利用此方法同理可得到天津市区内电动车道路利用效率为0.38(人·m)·(m2·s)-1，自行车为0.34(人·m)·(m2·s)-1，步行为0.48(人·m)·(m2·s)-1。

在天津市区目前的道路条件下，公共汽车道路利用效率为0.77(人·m)·(m2·s)-1，而小汽车道路利用效率仅为0.11(人·m)·(m2·s)-1，即完成同样运输量，小汽车出行道路占用面积是公共汽车的7倍、电动自行车出行的近4倍。载客量小、道路占用面积大的小汽车出行大量增加，严重挤占了原本十分稀缺的道路资源，势必造成道路交通拥堵，且导致空气严重污染。

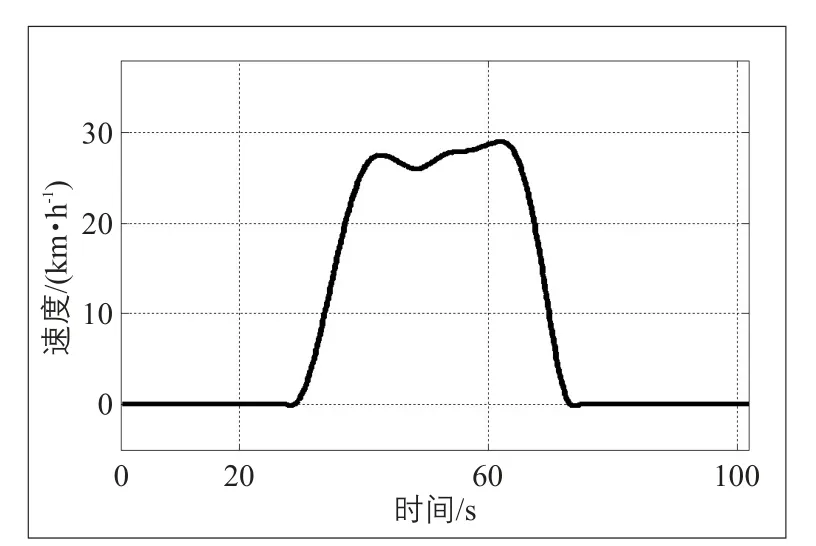
图5 小汽车行驶平均一个路谱周期的拟合曲线Fig.5 Fitted curve of cars driving in an average road spectrum cycle

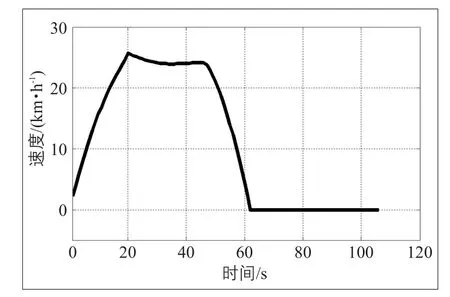
图6 公交行驶平均一个路谱周期的拟合曲线Fig.6 Fitted curve of buses driving in an average road spectrum cycle

4 结语

本文提出一种计算不同交通方式道路利用效率的理论与方法，从机理上反映不同交通方式的载客量、运输距离、运输速度、运输过程的占路面积和占路时间等交通要素对交通运输效率的影响，并将各种交通方式、交通状态、交通过程在统一的测度单位和测度模型中进行道路利用效率的定量分析，使它们具有可比性，以此定量鉴别优劣，为解决交通拥堵问题以及交通规划、管理、控制等提供定量分析手段，并可用于交通方案的定量评价和交通动态仿真分析。值得一提的是，本文提出的方法不仅可用于测度客运交通方式的道路利用效率，还可用于货运交通，以及轨道交通、航空等其他交通领域的交通资源利用效率的测度。

[1]魏立夏.城市路网交通运行效率评估研究[D].长沙：长沙理工大学，2012.Wei Lixia.Urban Road Network Traffic Opertaing Efficiency Assessment[D].Changsha:Changsha University of Science&Technology,2012.

[2]Gonzalez Guzman,Carlos Alberto,Robuste Francesc.Road Space Reallocation According to Car Congestion Externality[J].Journal of Urban Planning and Development,2011,137(3):281-290.

[3]Zhang Xiaoli,Chen Jun,Wang Wei,Jiang Dazhi.Efficiency and Equity Comparison of Urban Road Space Reallocation Schemes[C]//Peng Qiyuan,Kelvin C P Wang,Qiu Yanjun,Pu Yun,Luo Xia,Shuai Bin.Proceeding of the Second International Conference on Transportation Engineering (ICTE2009).USA:American Society of Civil Engineerings Press,2009:159-164.

[4]Sampaio B R,Neto O L,Sampaio Y.Efficiency Analysis of Public Transport Systems:Lessons for Institutional Planning[J].Transportation Research PartA,2008,42(3):445-454.

[5]吴世江，史其信，陆化普.基于交通效率的城市公共交通路网布局模型[J].土木工程学报，2005，38(1)：117-120.Wu Shijiang,Shi Qixin,Lu Huapu.Traffic Efficiency:Based Urban Public Traffic Network Distribution Model[J].China Civil Engineering Journal,2005,38(1):117-120.

[6]Mehar A,Chandra S,Velmurugan S.Passenger Car Units at Different Levels of Service for Capacity Analysis of Multilane Interurban Highways in India[J].Journal of Transportation Engineering,2014,140(1):81-88.

[7]Sheth C,Triantis K,Teodorovic D.Performance Evaluation of Bus Routes:A Provider and Passenger Perspective[J].Transportation Research Part E,2007,43(4):453-478.

[8]Holmgren J.The Efficiency of Public Transport Operations:An Evaluation Using Stochastic Frontier Analysis[J].Research in Transportation Economics,2013,39(1):50-57.