钢轨扣件减振橡胶阻尼耗能特性分析

王书卫

(铁道第三勘察设计院集团有限公司,天津　300251)



钢轨扣件减振橡胶阻尼耗能特性分析

王书卫

(铁道第三勘察设计院集团有限公司,天津300251)

摘要：为了掌握钢轨扣件减振橡胶中阻尼的分布及其随振幅和频率的变化规律,对减振橡胶元件受压和受剪两种扣件进行了试验研究。建立钢轨扣件减振橡胶非线性弹性力和混合阻尼叠加的动力学模型,完成模型参数识别及结果检验。根据所建立的动力学模型计算各试验工况下的弹性变形能、阻尼耗能和结构损耗因子。分析发现：压缩和剪切两种扣件减振橡胶的阻尼参数随振幅和频率的变化规律相似,弹性变形能、阻尼耗能和结构损耗因子均随振幅的增大而显著增大,而受频率的影响较小。相同工况下,压缩型扣件减振橡胶的结构损耗因子远大于剪切型扣件,说明压缩型扣件在发挥减振功能时,其耗能特性优于剪切型扣件,而隔振特性劣于剪切型扣件。因此,在钢轨扣件创新设计时,可以通过控制减振橡胶压-剪组合变形,来实现扣件隔振和衰减振动能量两功能的均衡发挥,将结构损耗因子作为设计过程中的控制指标。

关键词：钢轨扣件；橡胶；阻尼；结构损耗因子

钢轨扣件是现代轨道结构的重要组成部分，是降低轨道结构刚度的主要部件，其弹性及阻尼主要由其中的减振橡胶元件提供[1]。钢轨扣件的减振功能主要通过隔振和耗能两种途径实现，具体表现为扣件的弹性和阻尼。扣件的弹性能够缓冲列车振动通过道床向周围环境的传播，在一定程度上将振动能量隔离；扣件的阻尼能够消耗列车振动能量，在一定程度上将振动能量衰减。在工程实践中，需要均衡地发挥扣件的弹性和阻尼性能。如果阻尼过小，则不能有效地衰减列车振动能量；而如果阻尼过大，则减振橡胶会因为温度升高而造成老化加速，影响扣件寿命。因此，研究钢轨扣件减振橡胶每个振动周期阻尼耗能数量及所占振动能量的比重对扣件的优化创新设计具有重要意义。

研究表明，橡胶材料的阻尼耗能特性与材料的配方、振动幅值和振动频率等因素有关[2-4]；且橡胶材料在压、剪不同的受力状态下物理力学特性有较大的不同，使得由橡胶材料受压为主提供弹性的扣件与由橡胶材料受剪为主提供弹性的扣件在阻尼耗能特性方面也存在明显的差异。钢轨扣件的弹性主要由橡胶元件受压和受剪切两种方式来提供。由一定厚度的橡胶层的压缩变形为主来提供弹性的扣件称为压缩型扣件；由橡胶元件的剪切变形为主来提供弹性的扣件称为剪切型扣件。对压缩型和剪切型两种钢轨扣件进行了动态试验研究，分析钢轨扣件减振橡胶材料的阻尼耗能特性的影响因素和变化规律，以及阻尼耗能和弹性变形能分布规律，用以指导钢轨扣件的创新设计。

1钢轨扣件减振橡胶动力学模型

作为钢轨扣件减振元件的橡胶材料，由于其特殊的微观结构而兼具粘性液体和弹性固体的特性，在承受动态荷载时，其应变滞后于应力，即应力与应变之间存在一个相位差，使得一个周期内的应力-应变曲线呈一个闭合环，即所谓的应力应变迟滞曲线。目前对橡胶减振元件的动态建模，学者们普遍认为将橡胶材料非线性本构关系分解为非线性弹性恢复力和非线性阻尼力的耦合是合理的。恢复力的表达式可简单表示为

(1)

1.1非线性弹性恢复力

非线性弹性恢复力FK只是迟滞曲线的基架线，不消耗能量，可以用位移的奇次幂函数来表示[5，6]

(2)

其中，K2i-1(A，ω)为刚度系数；n为奇数，实际应用表明，n取3即可满足精度要求[7]。

1.2非线性阻尼力

1.2.1粘性阻尼

实际工程系统中的阻尼大多不是以单一形式存在，而是各种类型阻尼的非均质混合。为便于分析计算，在工程振动分析中通常将所讨论的阻尼划分为粘性阻尼和非粘性阻尼两大类。

其中粘性阻尼是最简单的一种阻尼形式，在线性振动系统的研究中讨论的多是粘性阻尼，即假定阻尼力的大小与振动速度成正比，方向与振动速度方向相反

(3)

其中，Fd为粘性阻尼；c为粘性阻尼系数。

为评价阻尼性能的优劣，通常用一个振动周期内阻尼所耗散的能量来表示。对于谐振系统x=Asinωt来说，一个振动周期内阻尼所耗散的能量为

(4)

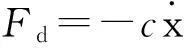
(5)

当振动系统有弹性力存在时，迟滞回线以弹性力曲线为长轴线，弹性力不消耗能量，迟滞回线面积不变。

1.2.2干摩擦阻尼

非粘性阻尼中最常见的是干摩擦阻尼，常用的干摩擦阻尼模型由Den Hartog提出，干摩擦力总是阻碍运动，与运动方向相反，其数学表达式为[8]

(6)

式中，μ为接触面的滑动摩擦系数；N为接触面正压力；Vret为两接触面的相对速度。

1.2.3混合阻尼

为扩大阻尼模型的描述范围，更加准确地拟合橡胶材料中实际存在的阻尼，拟采用一种包含粘性阻尼、干摩擦阻尼和高阶阻尼的模型，将阻尼描述为振幅A和圆频率ω的函数，则迟滞非线性阻尼力FC的表达式为

(7)

其中，C(A，ω)为阻尼系数；m(A，ω)为阻尼成分函数。m(A，ω)=0时，系统中阻尼为干摩擦阻尼；m(A，ω)=1时，阻尼为粘性阻尼，当01时，系统中阻尼为高阶阻尼。

(8)

将非线性弹性力与非线性阻尼力相叠加，可得钢轨扣件减振橡胶的数学模型为

(9)

2钢轨扣件减振橡胶动态特性试验

试验在SOS-200电液伺服动静试验机上进行。钢轨扣件在使用状态下，减振橡胶材料始终承受钢轨载荷及扣压件的扣压力，在列车荷载作用下产生动态应力-应变，整个过程减振橡胶始终处于受压状态，故在试验中对扣件施加一个预压力并采用正弦波位移激励法对扣件减振橡胶进行动态测试。试验中分别选用压缩型和剪切型两种扣件进行动态试验。橡胶材料为氯丁橡胶，硬度为邵氏70度，扯断强度为13 MPa。

在进行动态试验前，先对试验系统进行调试，并进行系统误差测试。然后根据扣件工作载荷范围测试选用的试验扣件的静刚度[9,10]，测得压缩型扣件的静刚度为27 kN/mm，剪切型扣件的静刚度为8.5 kN/mm。

根据减振橡胶实际工作条件下的受力情况，试验中设置初始预压力20 kN，动态载荷采用正弦位移激励函数x(t)=Asin(ωt+θ)+x0，A和ω分别为激励振幅和频率。由于钢轨扣件实际工作条件下承受的振动主频率在10 Hz左右[9]，故试验中选用激振频率范围为2～12 Hz，振幅范围为0.4～1.0 mm，可以得到不同工况下的恢复力-时间、位移-时间历程曲线。

剪切型扣件由于静刚度相对较小，允许变形量较大，试验中振幅分别取0.4，0.5，0.6，0.75，1.0 mm；频率分别取2，4，6，8，10，12 Hz。压缩型扣件静刚度较大，允许变形量较小，试验中振幅分别取0.4，0.5，0.6，0.7 mm；频率分别取2，4，6，8，10，12 Hz。将不同工况的恢复力时程曲线和位移时程曲线叠加就可得到力-位移迟滞回线。以压缩型扣件为例，相同振幅不同频率和相同频率不同振幅下的试验曲线如图1所示。

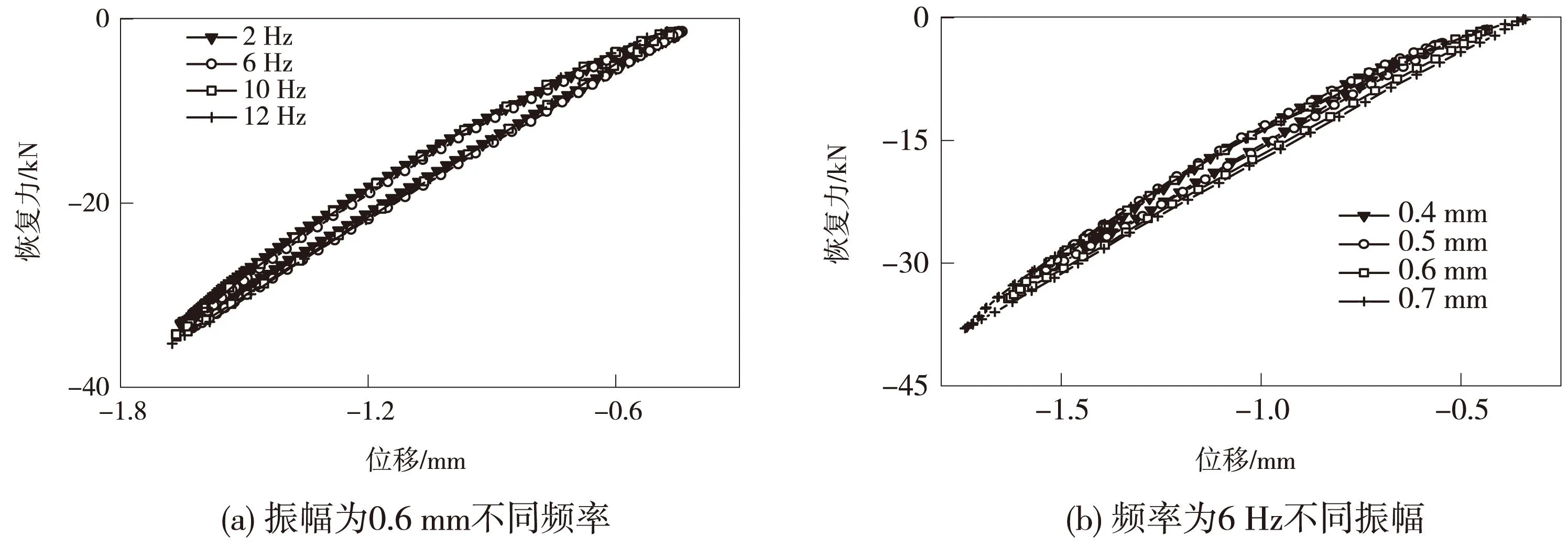
图1　压缩性扣件动态试验迟滞曲线

3试验结果与分析

3.1动力学模型参数识别及检验

将动态试验所得试验数据代入所建立的数学模型，采用曲线拟合的最小二乘法对各试验工况下的迟滞曲线进行参数识别，得到式(9)中相应的刚度系数、阻尼系数和阻尼成分函数的值。本文重点研究扣件减振橡胶阻尼耗能特性，部分工况的阻尼参数如表1、表2所示。

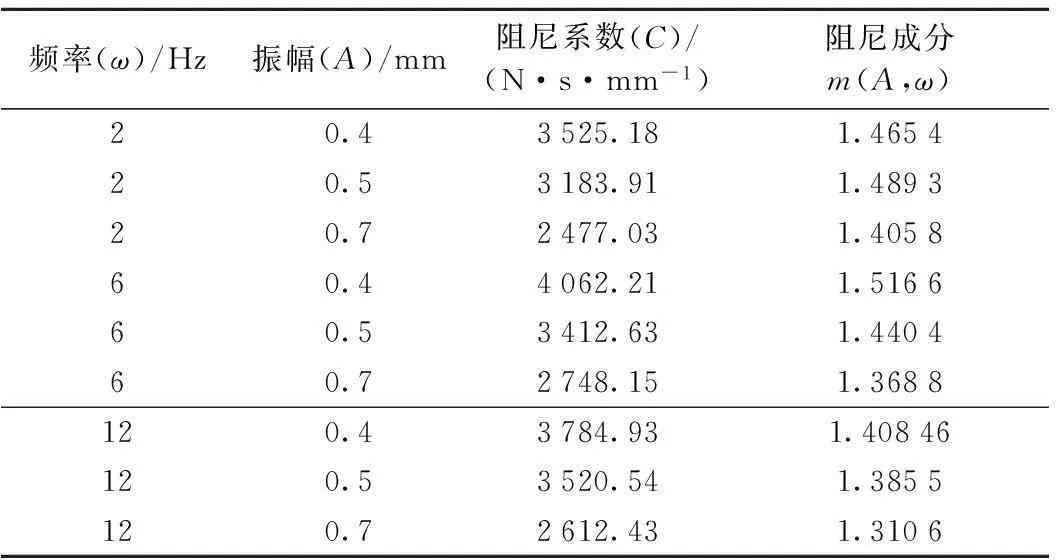
表1　压缩型扣件减振橡胶不同工况下的阻尼

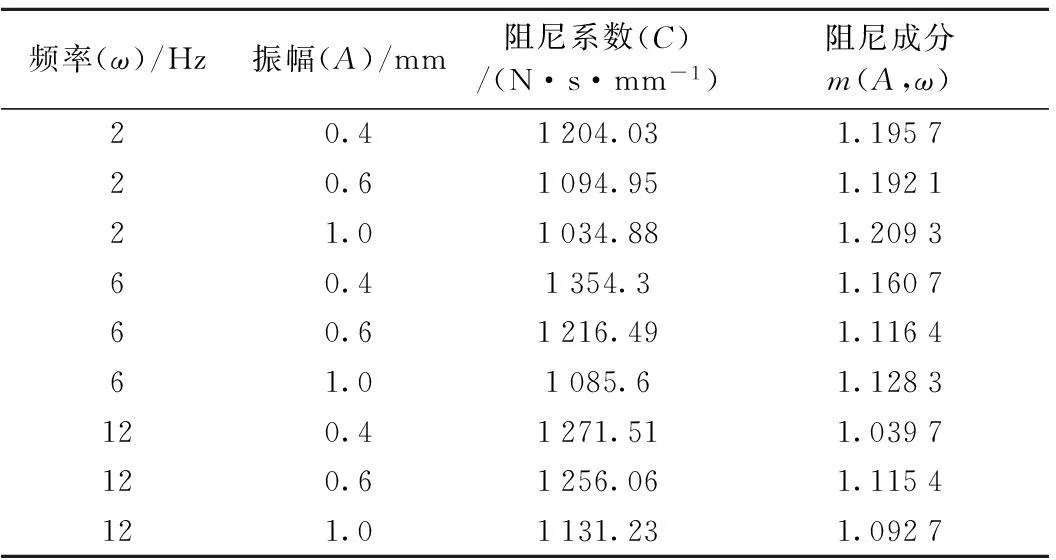
表2　剪切型扣件减振橡胶不同工况下的阻尼

根据非线性参数识别理论，基于Matlab平台进行曲线拟合，可得各阶刚度随振幅和频率变化曲线的表达式[7]，完成模型参数的识别。

为了验证参数识别的可靠性，根据参数识别结果，重构恢复力-位移迟滞曲线，与试验曲线作对比，以单一工况下压缩型扣件为例，检验结果如图2所示。结果显示，试验曲线和模型曲线能够很好地吻合，从而验证了所建立的钢轨扣件减振橡胶动力学模型的正确性。

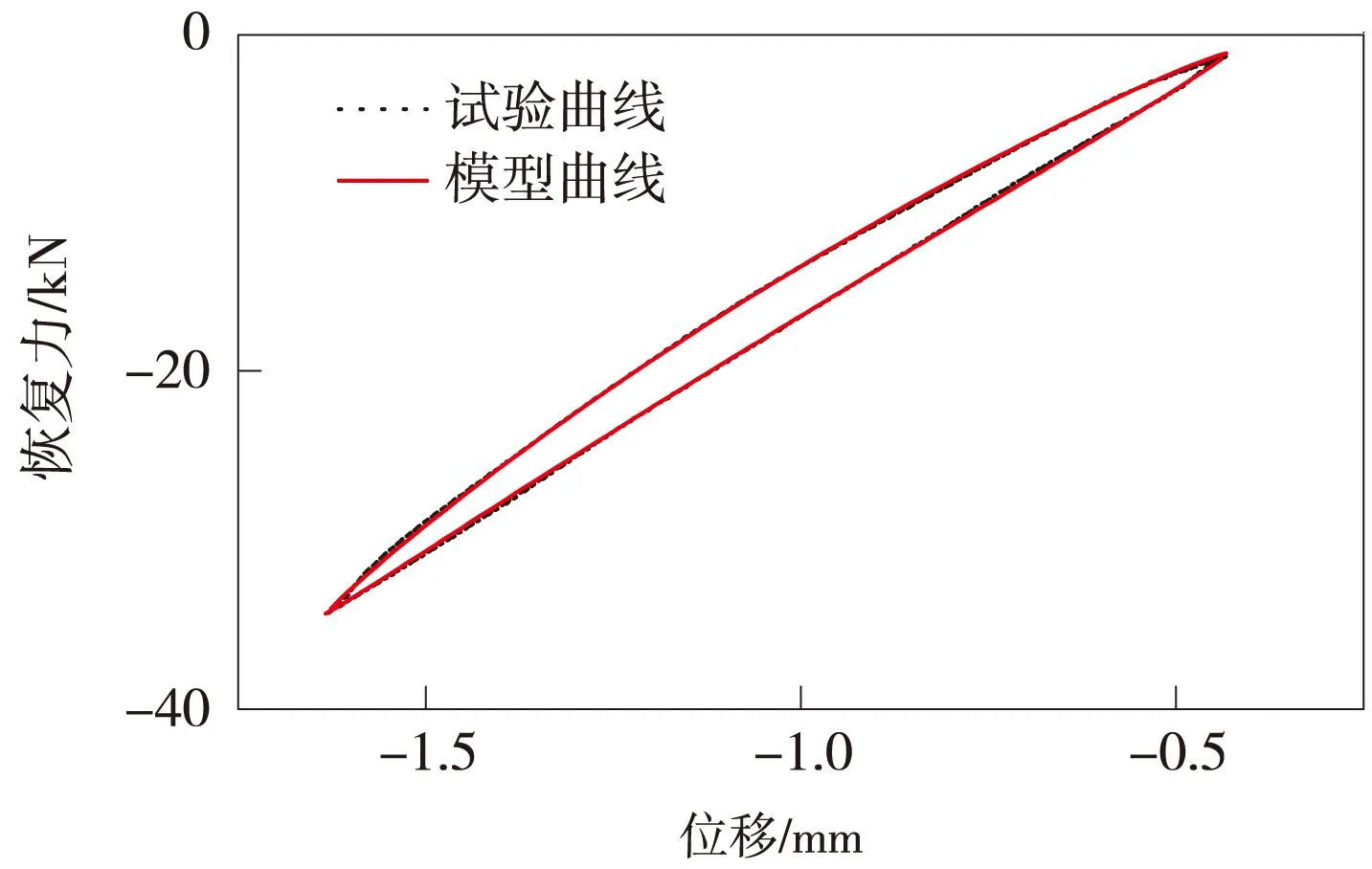
图2　模型曲线与试验曲线对比结果

3.2结构损耗因子的计算

由式(8)可知，阻尼系数是一个与纯阻尼迟滞环的长轴与短轴之比成正相关的函数，而纯阻尼迟滞环的长轴即为振幅，短轴取决于材料阻尼特性。表明阻尼系数不能很好地表征扣件减振橡胶随振幅的变化而发生的阻尼耗能特性的变化。且阻尼系数只能定性地表征结构的耗能性能，不能对扣件减振橡胶在动态激励下的能量损耗作定量分析。为了定量分析扣件减振橡胶的耗能，充分地描述两种不同类型扣件的阻尼性能并描述其振幅相关性，在此引入结构损耗因子。

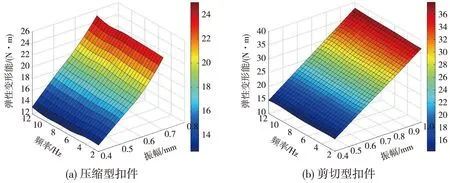
图4　弹性变形能随振幅和频率变化的三维图

用结构系统中耗损的能量与其弹性变形能的比值来描述阻尼，可以恰当地体现阻尼的物理本质，定义这一无量纲的比值为阻尼的损耗因子。用能量耗损的观点对机械结构的阻尼耗能量作定量分析，即为结构损耗因子[11]，如图3所示。

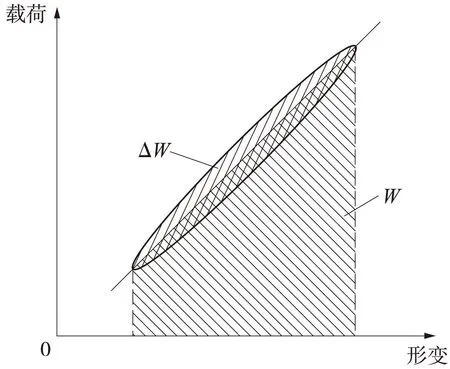
图3　结构耗损因子计算示意

结构耗损因子可由下式计算

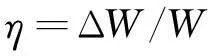
(10)

式中ΔW——阻尼耗能(迟滞环包围的面积)；

W——弹性变形能。

在MATLAB平台上对各工况下拟合所得的非线性弹性力和非线性阻尼力的曲线在振幅范围内进行积分，可得动态激励下每个振动周期的弹性变形能和阻尼耗能。进而由式(10)计算出各工况下的结构损耗因子。

3.3阻尼耗能特性分析

表1和表2中的拟合结果显示，阻尼系数随振幅的增大而减小，随频率的增大有增大的趋势。阻尼成分系数随振幅和频率的变化很小，且规律性不明显，压缩型扣件阻尼成分系数值在1.45左右，而剪切型扣件为1.2左右。两种扣件中的阻尼均为高阶阻尼，即动态激励作用下纯阻尼环较标准椭圆更为“尖细”。相同工况下的压缩型扣件的阻尼系数大于剪切型扣件，说明相同振幅和频率下，压缩型扣件的阻尼力大于剪切型扣件，每个振动周期会消耗更多的能量。

为了定量分析扣件减振橡胶每个振动周期的弹性变形能和阻尼耗能以及两者的分布状态和变化规律，必须对各工况的弹性变形能和阻尼耗能及结构损耗因子进行具体分析，此三参数各工况下的计算结果如图4～图6所示。

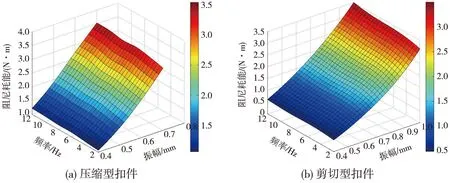
图5　阻尼耗能随振幅和频率变化的三维图

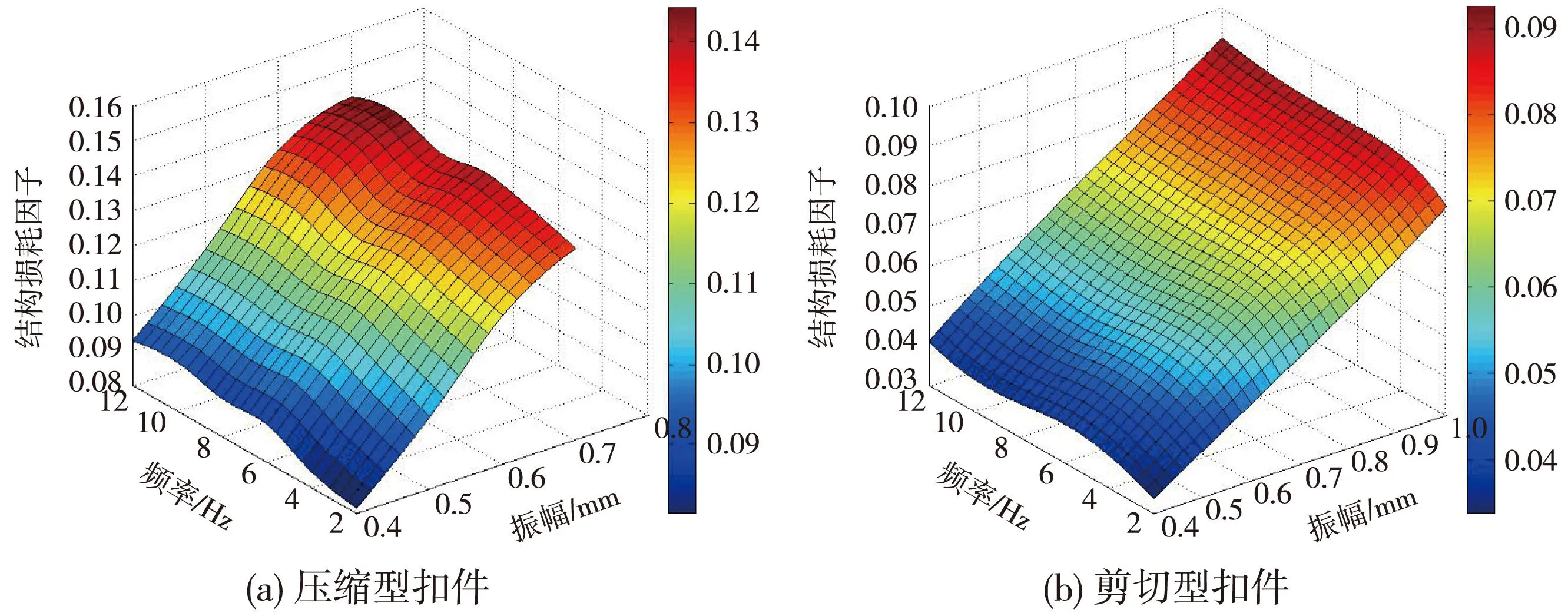
图6　结构损耗因子随振幅和频率变化的三维图

由图4可见，两种扣件减振橡胶在动态力作用下的弹性变形能随振幅的增大而显著增大。对比两种扣件减振橡胶的弹性变形能的变化曲线发现，随着振幅的增大，压缩型扣件减振橡胶弹性变形能的增大趋势逐渐增大；剪切型扣件减振橡胶弹性变形能随振幅的增大几乎呈线性增长。两种扣件减振橡胶在不同振幅下的弹性变形能随频率的变化十分微弱，可以认为其弹性变形能不受频率的影响。相同工况下，剪切型扣件减振橡胶的弹性变形能比压缩型扣件稍大。

由图5可见，两种扣件减振橡胶的阻尼耗能随振幅的增大而显著增大。对比两种扣件的阻尼耗能曲线发现，随着振幅的增大，压缩型扣件阻尼耗能的增大趋势有微弱的增加，而剪切型扣件阻尼耗能的增大趋势增加的较为明显。两种扣件阻尼耗能随频率的增加均有微弱的增大的趋势。相同工况下，压缩型扣件减振橡胶的阻尼耗能明显大于剪切型扣件。

由图6可见，两种扣件橡胶的结构损耗因子均随振幅的增大而显著增大。对比两种扣件橡胶的结构损耗因子随振幅的变化曲线发现，随着振幅的增大，压缩型扣件橡胶结构损耗因子的增大趋势逐渐减缓；而剪切型扣件橡胶结构损耗因子随着振幅的增大呈近似线性增长。两种扣件橡胶的结构损耗因子随频率的增大有微弱的增大的趋势，但变化并不单调。相同工况下，压缩型扣件减振橡胶结构损耗因子明显大于剪切型扣件。

计算结果显示结构损耗因子对振幅很敏感，受频率的影响很微弱，在此忽略频率的影响，将结构损耗因子表示成振幅的函数，其函数关系表示为

(11)

用非线性参数拟合的最小二乘法，对压缩型和剪切型两种扣件橡胶结构损耗因子的计算结果进行数据拟合，可得结构损耗因子与振幅关系的表达式

(12)

(13)

4结论

钢轨扣件减振橡胶中阻尼系数随振幅的增大而减小，随频率的增大有增大的趋势；压缩型扣件减振橡胶阻尼系数大于剪切型扣件。其中阻尼为高阶阻尼，相比压缩型扣件，剪切型扣件减振橡胶中阻尼更接近粘性阻尼。对扣件减振橡胶中阻尼耗能进行定量分析有如下结论。

(1)压缩型和剪切型扣件减振橡胶弹性变形能随振幅的增大而显著增大；频率的变化对其影响十分微弱，可忽略。相同工况下，剪切型扣件减振橡胶的弹性变形能比压缩型扣件稍大。

(2)两种扣件减振橡胶的阻尼耗能随振幅的增大而显著增大，且随着振幅的增加，阻尼耗能的增幅有增大的趋势，剪切型扣件的这种趋势更为明显；两种扣件的阻尼耗能随频率的增加均有微弱的增大的趋势，但变化不单调。相同工况下，压缩型扣件减振橡胶的阻尼耗能明显大于剪切型扣件。因此在钢轨扣件设计时应控制减振橡胶材料的变形幅度，避免因追求低刚度使橡胶材料变形幅度过大，造成阻尼耗能的大幅度增加，加速橡胶老化。

(3)两种扣件减振橡胶的结构损耗因子均随振幅

的增大而显著增大，随着振幅的增加，压缩性扣件减振橡胶结构损耗因子的增大趋势逐渐减缓，而剪切型扣件几乎呈线性增长；两种扣件的结构损耗因子随频率的增加均有微弱的增大的趋势，但变化不单调。相同工况下，压缩型扣件减振橡胶的结构损耗因子远大于剪切型扣件，说明在工作条件下，压缩型扣件在发挥减振功能时，其耗能特性优于剪切型扣件，而其隔振特性劣于剪切型扣件。

减振型钢轨扣件多采用压-剪组合变形来提供弹性，在对钢轨扣件进行低刚度[12]设计时，为了在增大减振橡胶材料变形幅度的同时不使阻尼耗能大幅增加，可增加橡胶材料剪切变形提供弹性的比例，同时应将变形幅度控制在阻尼耗能不至影响橡胶寿命范围以内。而钢轨扣件设计刚度相对较大时，可增加压缩变形提供弹性的比例，保证系统振动能量的有效衰减。总之，在钢轨扣件设计过程中，通过控制减振橡胶不同的压-剪变形组合，可实现钢轨扣件隔振与衰减振动能量两功能的均衡发挥，而结构损耗因子可作为设计过程中的控制指标。

参考文献：

[1]Xiao Xinbao, Jin Xuesong， Wen Zefeng.Effect of disabled fastening systems and ballast on vehicle derailment[J]. Journal of Vibration and Acoustics， 2007，129(2):217-229．

[2]韩德宝，宋希庚.橡胶减振器非线性动态特性的试验研究[J].振动工程学报，2008，2(21):102-106．

[3]胡振娴，顾亮.汽车减振器橡胶连接件动态特性实验研究[J].北京理工大学学报，2010，30(4):410-414．

[4]Tian Ran Lin， Nabil H Farag， Jie Pan. Evaluation of frequency dependent rubber mount stiffness and damping by impact test[J]. Applied Acoustics， 2005，66:829-844．

[5]Dong X， Hougbton J R. Structural damping measurement under random excitation[C]∥Proceedings of the 15th International Modal Analysis Conference. Japan， Tokyo， 1997:497-503．

[6]李莉，王书卫，吕英康，刘艳.钢轨扣件减振橡胶动态刚度特性分析[J].同济大学学报：自然科学版，2013，41(2):208-212．

[7]刘艳，罗雁云.钢轨扣件减振橡胶动态特性分析[J].中南大学学报：自然科学版，2011，42(9)：2875-2880．

[8]J.P.DenHartog. Forced vibration with combined coulomb and viscous friction[J]. Trans. ASME，1931:52-55.

[9]瞿连辉.城市轨道交通用减振扣件的试验方法[J].橡胶工业，2009(56):250-255．

[10]张健，王书卫，罗雁云.不同受力环境下的钢轨扣件减振橡胶动态特性[J].铁道科学与工程学报，2013，10(4):52-58．

[11]戴德沛.阻尼技术的工程应用[M].北京：清华大学出版社,1990:34-40．

[12]王其昌.无砟轨道钢轨扣件[M].成都：西南交通大学出版社，2006:115-116.

Analysis of Structural Damping Property of Rail Fastening Rubber Absorber WANG Shu-wei

(The Third Railway Survey and Design Institute Group Corporation, Tianjin 300251, China)

Abstract：To understand the rules of damping distribution and changes in amplitude and frequency of rubber absorber of rail fastening, two kinds of rail fastenings with compressed and sheared rubber absorbers respectively are tested. A nonlinear dynamic model of rubber absorber coupled with nonlinear elastic force and mixed damping in rail fastening is established with model parameters identified and results verified. Elastic deformation energy, damping dissipation energy and structural loss factors are calculated based on the proposed model. The results show that calculated damping parameters of the two rubber absorbers follow the similar rules, the elastic deformation energy, damping dissipation energy and structural loss factor increase rapidly with the increasing of amplitude, and are affected less by frequency. Structural loss factor of the compressed rubber absorber is much bigger than that of sheared rubber absorber under the same experimental condition, which indicates that the compressed rubber absorber has a better damping capacity than that of the sheared rubber absorber, but the sheared rubber absorber has a better capacity of vibration isolation. As a result, vibration isolation and energy dissipation can be balanced through combined deformation of compressed and sheared rubber absorbers to design new rail fastenings, and structural loss factor taken as a control index.

Key words：Rail fastening; Rubber; Damping; Structural loss factor

中图分类号：U213.5

文献标识码：A

DOI:10.13238/j.issn.1004-2954.2015.01.009

文章编号：1004-2954(2015)01-0037-05

作者简介：王书卫(1988—)，男，助理工程师，2013年毕业于同济大学轨道工程专业，工学硕士，E-mail：xianwangshu@sina.com。

收稿日期：2014-11-03