被动微波遥感积雪参数反演方法进展

孙知文， 于鹏珊， 夏浪， 武胜利， 蒋玲梅， 郭镭

(1.航天恒星科技有限公司，北京 100086；2.北京神舟航天软件技术有限公司，北京 100094；3.农业部资源遥感与数字农业重点开放实验室，北京 100081；4.国家卫星气象中心，北京 100081；5.北京师范大学遥感科学国家重点实验室，北京 100875)

被动微波遥感积雪参数反演方法进展

孙知文1， 于鹏珊2， 夏浪3， 武胜利4， 蒋玲梅5， 郭镭1

(1.航天恒星科技有限公司，北京 100086；2.北京神舟航天软件技术有限公司，北京 100094；3.农业部资源遥感与数字农业重点开放实验室，北京 100081；4.国家卫星气象中心，北京 100081；5.北京师范大学遥感科学国家重点实验室，北京 100875)

雪深(snow depth，SD)和雪水当量(snow water equivalent，SWE)是气候水文研究中的重要参数，在雪灾监测中尤为重要。首先,简要介绍了被动微波遥感SD和SWE反演算法的物理基础——积雪微波辐射传输模型，分析了不同微波频段、不同特点的积雪微波辐射和散射特性。然后，根据前人的研究从数学角度将反演算法分为线性亮温梯度法和基于先验知识法，总结了2类算法的优势和局限性： 线性亮温梯度法相对简单、速度快，一般只适用于特定的研究区；先验知识法需要获取研究区的样本数据，并反复训练才能达到较好的精度，但对样本的独立性及其均值差异显著性的要求较高。最后，重点介绍了我国风云三号微波成像仪(FY-3 MWRI)的全球SD和SWE反演算法和针对中国区域的改进算法，并对未来的研究热点进行了展望。

被动微波遥感；微波辐射计；雪深(SD)；雪水当量(SWE)；反演算法

0 引言

积雪是地球表面最活跃的气象要素之一，影响着区域乃至全球的能量和水汽平衡。积雪参数是中长期气候数值预报模式和陆表水文模型中的重要参数，在气候模式、径流预报、水资源管理、雪灾和洪涝监测中有重要应用。遥感技术能快速有效、大范围地监测积雪[1-12]。国内外积雪遥感监测主要有光学雪覆盖监测及微波反演雪深(snow depth，SD)和雪水当量(snow water equivalent，SWE)，光学传感器能够监测季节性积雪的覆盖面积，但不能有效估算SD和SWE；微波则能够穿透雪层、探测雪层信息，弥补了光学遥感的不足，是大范围、全天候监测SD和SWE的重要手段[13-17]。

自1978年起，经过30余a星载被动微波辐射计的设计和工艺水平的不断提高，由早期的低时空分辨率、单频率、单极化的探测方式，逐渐发展为高时空分辨率、多频率、多极化的探测方式，使积雪参数的估算精度也随之提高。国内外业务化运行的星载被动微波辐射计包括Nimbus-7 SMMR[18]，DMSP-SSM/I[19]，AQUA AMSR-E[20]，FY-3 MWRI[21]和GCOM-W1 AMSR2等，能定量估算区域和全球的积雪储量及其变化趋势，为全球用户提供积雪监测数据的业务化服务。

本文简要介绍了被动微波积雪参数反演的理论基础和模型；讨论了不同反演算法的优点和不足；最后介绍我国极轨气象卫星风云三号微波成像仪(FY-3 MWRI)的SD和SWE的反演算法，为被动微波遥感数据在积雪参数反演中的深入应用提供参考。

1 积雪反演理论基础

1.1 被动微波反演理论基础

如图1所示，被动微波辐射传输模型描述了微波通过粗糙地表、非均匀致密介质(如积雪)和大气之间的辐射和散射过程[22]，是被动微波积雪反演的基础。

(Z为深度；ε为介电常数；μ为介质磁导率；θ为入射角；φ为出射角；T+,T-分别为雪层上、下行辐射强度)图1 来自地表和雪层的微波发射Fig.1 Microwave emissivity from land surface and snowpack

由于雪层为非均匀介质层，微波要经过多次散射和吸收过程。雪层界面的上行和下行辐射可用2个方程表示为

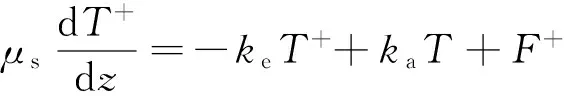
(1)

(2)

式中：μs为介质向上的总辐射；z为深度；T+,T-分别为雪层上、下行辐射强度；ke为雪层衰减系数；T为雪层温度廓线；ka为雪层吸收系数；F±分别为雪颗粒的向上和向下的散射项。用于迭代求解的辐射传输方程为

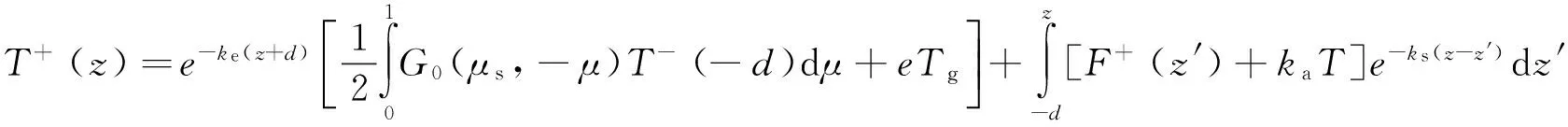
(3)

(4)

式中：G0(μs,-μ)为下表面散射相位阵的零阶傅立叶项；S0(μs,-μ)为上表面散射相位阵的零阶傅立叶项；e为下边界辐射率；z′为深度；Tg为下层介质半空间温度。

利用式(3)可计算出z=0处的上行辐射亮温。上述方程无解析解，通常采用数值方法求解，求解过程中需要使用积雪模型描述地表辐射、雪层的消光和发射以及各介质层之间的边界条件等物理过程。积雪的微波辐射模型主要有： 早期的散射层微波发射模型[23]、赫尔辛基大学积雪微波发射模型(HUT snow emission model，HUT)[24]、积雪多层微波辐射传输模型(microwave emission model of layered snowpacks，MEMLS)[25]和基于致密介质辐射传输(dense medium radiative transfer，DMRT)理论的积雪模型[26-28]。上述模型在很多专著和文献中都有详细的论述[5-8]。

1.2 积雪参数对微波信号影响分析

大量研究[9-11]表明，干雪的微波辐射随雪的深度、颗粒大小、密度和结构的变化而变化；低频微波对地面参数较为敏感，高频微波则对体散射内的颗粒大小、形状等较为敏感；当存在液态水时，地表和冰之间存在介电常数差异，积雪的微波辐射得到增强[29]。

建立积雪反演算法需要考虑的因子包括雪密度、颗粒大小、雪深、微波频率、极化方式和入射角等。蒋玲梅[9]使用改进的积分方程模型(advanced integrated equation model，AIEM)模拟积雪的结果表明： 在入射角为45°、积雪平均粒径为0.3 mm、频率为18.7 GHz时，亮温随雪深的增加而略有增加；但在频率为36.5 GHz时，无论是什么样的颗粒大小，当雪深增加时亮温值都下降，而且很快饱和。在积雪粒径很小时，雪深与亮温差之间存在线性关系；但在积雪粒径较大时，随着积雪厚度的增加，雪深与亮温差之间存在非线性关系。高频89 GHz由于散射作用，密度与 89 GHz 的极化比的对数成线性关系。除此之外，积雪地表的含水量及其上覆的植被和积雪的介电常数、雪层的不均一性等都会影响积雪参数的反演精度。

因此，SD和SWE的反演非常复杂，需要在必要的前提条件和假设下，建立辐射计探测得到的微波亮温与SD和SWE的数学关系。在算法中综合考虑不同的影响因子是准确估算SD和SWE的关键。

2 SD和SWE反演算法

研究人员发展了大量基于被动微波遥感数据的SD和SWE反演算法，本文从数学方法的角度将这些反演方法分为2类： 线性亮温梯度法和基于先验知识法。

2.1 线性亮温梯度法

微波亮温是积雪后向散射系数的函数。后向散射系数与微波频率成正比，导致积雪的亮温梯度为负。假定积雪为均一、单层的干雪，雪密度为常数，雪的颗粒大小不变，雪深不超过1 m，由于雪颗粒对来自地表的高频或低频的微波散射强度不同，因而造成不同频段的微波辐射亮温存在差异，并且随着积雪深度的增加亮温梯度增大。通常可将微波亮温与SD和SWE之间的关系描述成线性关系。

在实际应用中,使用星载微波辐射计反演全球或区域积雪参数时，不同的研究人员根据不同微波频段和/或不同研究区特点，给出不同的系数。不同反演算法的差异主要是由于系数获取方式的不同和考虑了植被、雪颗粒大小等参数的影响造成的。根据系数获取方法的不同，线性亮温梯度法可分为3种： 静态算法、动态算法和静态与动态结合的算法。

2.1.1 静态反演算法

针对裸地上的积雪反演算法是静态算法中较为经典的算法，最初由Chang等[30]建立，计算式为

SD=k0+k1·△Tb，

(5)

或

SWE=k0+k1·△Tb。

(6)

式(5)(6)中：SD为雪深，cm；SWE为雪水当量，mm；△Tb为不同频率、不同极化下的亮温差；k0和k1为常数，由研究人员根据研究区域给出。SWE与SD的换算关系为

SWE=10ρ·SD，

(7)

式中ρ为积雪密度。

对于星载微波辐射计而言，△Tb大多采用K和Ka波段同极化的亮温差，如 AMSR-E和FY-3 MWRI分别使用频率为18.7 GHz和36.5 GHz时的水平极化亮温差。

森林地区的植被削弱了下伏雪盖的微波辐射，而植被冠层自身的发射则增加了星载辐射计接收到的微波辐射；若不考虑植被，反演算法会低估森林地区的SWE[31]，可将式(6)修订为

(8)

式中fc是像元内的森林覆盖率。森林覆盖率可通过高分辨率光学传感器观测到的植被指数百分比或反照率计算得出。

2.1.2 动态反演算法

自然积雪在演变过程中，其物理特性都会随着时间和空间动态变化[32]，而静态算法未考虑积雪的年际变化特性。动态算法则考虑了积雪内部特性随时间和空间变化而发生的变化，尤其是颗粒大小的变化。Josberger等[16]利用积雪的热辐射梯度来描述积雪随时空变化的质变过程，用热辐射指数(thermal gradient index，TGI)来表示积雪层内热温度梯度，作为衡量颗粒增长的指标，即

(9)

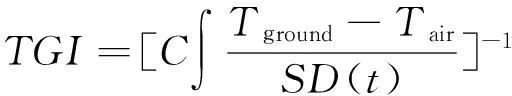
(9)

式中：C为临界温度梯度值，是一个常数(C=20 ℃/m)；Tground为下垫面地表-雪界面温度；Tair为空气-雪界面温度；SD(t)为雪深。

研究过程中发现，亮温梯度SG与热辐射指数TGI之间存在很好的线性关系，即

SG=α·TGI+β,

(10)

式中α，β为经验系数。

对式(10)取导数，则SD(t)可表示成

(11)

该动态算法假设地表温度接近于0℃，通过研究区密集气象台站数据来验证卫星反演的雪深，在美国北部大平原中精度比静态算法高，但在针叶林和极地地区不适用。

另外一类动态算法同时考虑植被覆盖度和积雪物理特性。如Kelly等[33]在静态算法基础上，综合考虑植被覆盖度、积雪颗粒大小和密度在时间和空间上的动态变化，采用基于辐射传输的半经验模型来描述积雪颗粒大小和密度随时空变化的演变过程。利用气象台站连续日积雪测量值与SSM/I数据,建立了动态反演算法，即

SD=k0(△Tb)2+k1·△Tb,

(12)

式中：k0和k1分别为与积雪粒径大小和密度相关的气候参数。

2.1.3 静态与动态结合反演算法

大范围地区内的积雪在空间上的变化会很大，加之冬季北半球大部分冻土区的地表空气温度非常低，永冻层的存在强烈影响着地表温度，因而积雪的颗粒大小随着温度的下降而增长，而且随着温度梯度变大很容易形成霜壳。动态反演算法考虑了这些因素的影响，因而在冬初反演精度较好，而在冬末由于颗粒增长缓慢会使反演精度较差。

Grippa等[34]把动态和静态算法相结合，用每月的气象雪深数据来调整静态算法中的系数；当亮温梯度变化不大时则采用静态算法，而亮温梯度变化较大时则采用动态算法。静态与动态结合的反演算法在长时间气候变化的情况下应用效果较好，因而在研究气候和生态系统变化时经常使用。

2.2 基于先验知识法

2.2.1 神经网络法

当雪深超过1 m、积雪粒径较大时，用线性关系并不能准确描述SD和SWE与微波亮温之间的非线性关系。人工神经网络模型被广泛用于解决各类非线性问题。通常使用神经网络法反演地表参数的步骤如下： 将采集的样本数据随机分成2组，一组为训练数据，另一组为测试数据；在反复训练和测试评估过程中，使用不同极化和频段的组合使得SWE反演最稳定且精度最高，最终将微波亮温与SWE进行神经网络建模。训练过程中使用的通道越多，就越容易克服积雪物理特性、地表粗糙度和植被的影响。Choudhury等[35]用神经网络技术反演积雪层的3个参数： 平均颗粒大小、积雪密度和温度。Tedesco等[19]使用水文模型作为边界限定，将神经网络与耦合水文模型相结合进行积雪参数反演。

2.2.2 贝叶斯反演法

把模糊的前向模型(前向算法)转化为数据驱动的前向模型作为贝叶斯模型的驱动条件，将先验知识如地面实测数据、先验概率、噪声分布等信息作为贝叶斯迭代法的限制条件，使得迭代解很快收敛，反演出结果。Davis等[36]对微波前向模型使用贝叶斯迭代反演积雪参数，使用Nimbus-7 SMMR数据作为算法输入，经验证表明，反演结果优于线性亮温梯度法。

2.2.3 其他反演法

除神经网络法和贝叶斯法外，Durand等[37]利用马尔科夫链蒙特卡罗方法反演SWE。雪层的数量由选定模型的判据创建的一系列马尔科夫链确定，在每一个马尔科夫链中模拟积雪层的厚度、密度、颗粒度大小和温度。结果表明，该方法对于浅雪反演效果较好，RMSE<18.2 mm；对于深雪则误差较大，需要在算法中引入更多的先验参数。

2.3 反演方法小结

线性亮温梯度法是基于前向模型的经验、半经验算法，具有算法形式简单、计算速度快、可对卫星数据实时处理等特点。研究人员根据研究区内积雪和其他影响因素的特征，将这些影响归一化到2个回归系数k0，k1中，在研究区内的反演精度较好，基本上能满足大尺度气候和水文模式的精度要求。但同时也存在着一些问题，如算法的区域性较强，为保证精度，需要对系数经常更新；在机理上还没有完全搞清辐射计探测到的亮温与地表辐射的复杂关系，尚没有一个适用性很强的模型实现SD和SWE的高精度估算。

基于先验知识训练的反演模型能较好地描述微波亮温与积雪参数之间的非线性关系，所建立的模型在应用于实际反演时，不再需要地表的任何先验知识，克服了经验、半经验算法应用于不同研究区时的局限性，是解决反演问题的一个强有力的工具。但同时此类算法也存在一定的局限性： 模型建立时需要积累大量的训练样本，输入参数必须是相关性小的独立参数，否则训练结果误差大；训练算法和结构也是模型成功的关键[38]，该算法虽然适用范围广泛、精度高，但在反演机理上无实际的物理意义。上述因素都限制了神经网络反演算法的应用。因此，该方法常用于科学研究中，在实际卫星业务运行中基本不使用。

3 FY-3 MWRI的SD和SWE算法

我国星载被动微波辐射计起步较晚，2008年发射的风云三号(FY-3)A星搭载的微波成像仪(microwave radiation imager，MWRI)是我国首个获取SD和SWE的业务化运行的有效载荷，它能够提供全球和中国区的积雪参数产品[39]。MWRI的各项性能指标见表1。

表1 FY-3微波成像仪性能指标Tab.1 Performance index of FY-3 MWRI

FY-3 MWRI 的SD和SWE反演算法有2种： 全球算法和中国区域算法。

3.1 全球算法

FY-3 MWRI的积雪参数全球算法在AQUA/AMSR-E的全球算法[40]的基础上针对MWRI仪器特性发展而来。该算法考虑了以下因素：

1)植被。对有森林覆盖的积雪区，使用森林覆盖率和森林密度对亮温进行校正；

2)降雨。对降雨的判别可用散射指数的阈值进行，同时将质量标志标识为降雨；

3)湿雪。湿雪的介电常数较大，致使微波信号急剧变化。计算过程中遇到湿雪则不反演，将质量标志标识为湿雪，供用户酌情使用；

4)高海拔山区。由于受地表粗糙度、冻土、山地湖泊等的影响，加上卫星升降轨的观测方向不同，山地地区SD和SWE的反演变得更加复杂，SWE精度的可信度将会下降。计算过程中将质量标志标识为山区，供用户酌情使用。

FY-3 MWRI的积雪参数全球算法的核心公式为

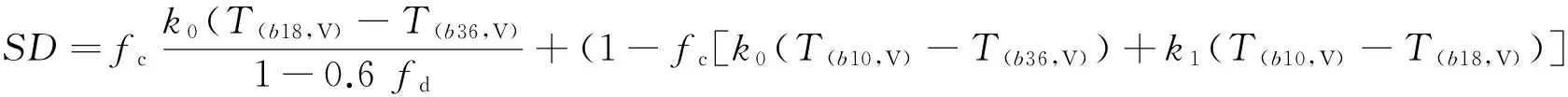
(13)

式中：SD为雪深，cm；fc为森林覆盖率；fd为森林密度；k0和k1分别为中心频率在18 GHz和36 GHz的极化修正系数；T(b10,V)，T(b18,V)和T(b36,V)分别为10 GHz，18 GHz和36 GHz通道的垂直极化亮温。使用式(7)计算SWE。

具体的算法流程如图2所示。

图2 FY-3 MWRI的SD和SWE反演算法流程Fig.2 Flow chart of SD and SWE inversion algorithm for FY-3 MWRI

3.2 中国区域算法

与全球算法不同的是在中国季节性降雪区内，中国区域积雪参数反演算法考虑了4种类型的积雪覆盖地表： 森林、草地、裸地和耕地，针对这4种类型的地表覆盖给出了一组经验公式。SD是不同地表特征下雪深的加权和，权重系数是不同地表各自占陆地的百分比。计算SD的基本公式为

SD=fbarrenSDbarren+fgrassSDgrass+fforestSDforest+

ffarmSDfarm,

(14)

式中：f为不同类型地表覆盖所占陆地的百分比；SD为不同地表类型上的雪深。

SWE依据式(7)、通过使用气象台站观测数据回归建立的经验算法计算得到。与实测数据的对比结果表明，FY-3 MWRI的区域算法在中国区域内的SWE反演精度优于AMSR-E的全球算法，而AMSR-E的全球算法会高估中国区域内的SWE[41]。

4 结论

被动微波遥感反演雪深(SD)和雪水当量(SWE)依然是当前研究的难点。全球范围业务化运行的星载微波辐射计反演算法以线性亮温梯度法为主。利用微波辐射计监测积雪的业务化运行的星载辐射计主要有： 搭载在Nimbus-7上的SMMR是单极化5个频率(6～37 GHz之间)的辐射计，从1978年起SMMR业务化获取SD和SWE等参数，一直运行至1987年。1987年美国国防气象卫星(DMSP)携载SSM/I升空，SSM/I是H和V极化7个频段的辐射计。2002年AQVA上的AMSR-E开始工作，仪器性能的改进使得被动微波遥感的低空间分辨率得到很大改进。2011年10月起AMSR-E停止工作，由日本AMSR2接替。中国的风云三号微波成像仪器(FY-3 MWRI)自2008年起开始业务化服务。

经过30余a的研究，被动微波遥感反演SD和SWE取得了很大进展，但后续研究更应关注以下几个方面的问题：

1)雪层中的含水量是影响被动微波遥感反演SD的重要因素，也是反演的难点。特别是在积雪融化时，表面介电常数显著改变[42]，表面含水量每增加1%，19 GHz频率的微波穿透深度减小10 cm, 37 GHz的微波穿透深度更小。可见对湿雪SD的反演依然存在技术上的缺陷。

2)反演精度验证方法的改进也是反演算法改进的重点之一。被动微波遥感的空间分辨率低，K波段和Ka波段的地面分辨率只有25 km，难以准确获取如此大尺度的积雪空间信息对算法进行验证。

3)星载微波辐射计C波段和X波段受地面通讯干扰，使观测亮温受到污染。主流的星载被动微波辐射计(如DMSP-SSM/I，AQUA AMSR-E，FY-3 MWRI等)的星载微波辐射计的不同通道都会受到地面通讯不同程度的影响。

4)随着陆表数据同化研究的兴起，对星载辐射计积雪反演产品进行同化也将是积雪研究的一个重要方向。使用同化方法将积雪前向模型与微波观测数据结合，用数据同化方式解决反演本身存在的缺陷，可为提高SD和SWE的反演精度提供新途径。

[1] Hall D K,Riggs G A,Salomonson V V.MODIS/AQUA snow cover 8-day L3 global 0. 05deg CMG Version 5[DB/OL].Boulder, Colorado USA: National Snow and Ice Data Center.Digital media,2007,updated daily.http://nsidc.org/data/myd10c2.html.

[2] 王世杰.利用NOAA/AVHRR影像资料估算积雪量的方法探讨[J].冰川冻土,1998,20(1):68-73. Wang S J.Exploring the estimation of snowpack volume with NOAA/AVHRR satellite data[J].Journal of Glaciology and Geocryology,1998,20(1):68-73.

[3] Hall D,Riggs G,Salomonson V V.Development of methods for mapping global snow cover using moderate resolution imaging spectroradiometer data[J].Remote Sensing of Environment,1995,54(2):127-140.

[4] 周咏梅,贾生海,刘萍.利用NOAA-AVHRR资料估算积雪参量[J].气象科学,200l,21(1):117-121. Zhou Y M,Jia S H,Liu P.The method of snowcover parameters estimation using NOAA-AVHRR data[J].Scientia Meteorologica Sinica,2001,21(1):117-121.

[5] (美)乌拉比F T,穆尔 R K,冯建超.微波遥感[M].北京:科学出版社,1986. Ulaby F T,Moore R K,Fung J C.Microwave Remote Sensing:Active and Passive[M].Norwood, MA:Artech House,1986.

[6] 金亚秋.电磁散射和热辐射的遥感理论[M].北京:科学出版社,1993. Jin Y Q.Remote Sensing Theory of Electromagnetic Scattering and Thermal Emission[M].Beijing:Science Press,1993.

[7] (美)霍尔 D K,马丁内克 J.冰雪遥感[M].顾钟炜,陈贤章,冯学智,等译.兰州:甘肃科学技术出版社,1991. Hall D K,Martinec J.Remote Sensing of Ice and Snow[M].London:Chapman and Hall,1985.

[8] Tsang L,Kong J A,Shin R T.Theory of Microwave Remote Sensing[M].New York:Wiley,1985.

[9] 蒋玲梅.被动微波雪水当量研究[D].北京:北京师范大学,2005. Jiang L M.Passive Microwave Remote Sensing of Snow Water Equivalence Study[D].Beijing:Beijing Normal University,2005.

[10]Tsang L,Kong J A.Multiple scattering of electromagnetic waves by random distribution of discrete scatterers with coherent potential and quantum mechanical formalism[J].Journal of Applied Physics,1980,51(7):3465-3485.

[11]Armstrong R L,Brodzik M J.Recent northen hemisphere snow extent:A comparison of data derived from visible and microwave satellite sensors[J].Geophysical Research Letters,2001,28(19):3673-3676.

[12]车涛,李新,高峰.青藏高原积雪深度和雪水当量的被动微波遥感反演[J].冰川冻土,2004,26(3):363-368. Che T,Li X,Gao F.Estimation of snow water equivalent in the Tibetan Plateau using passive microwave remote sensing data(SSM/I)[J].Journal of Glaciology and Geocryology,2004,26(3):363-368.

[13]Martinec J.Expected snow loads on structures from incomplete hydrological data[J].Journal of Glaciology,1978,19:185-195.

[14]Bernier P Y.Microwave remote sensing of snowpack properties:Potential and limitations[J].Nordic Hydrology,1987,18(1):1-20.

[15]Rango A,Chang A T C,Foster J L.The utilization of spaceborne microwave radiometers for monitoring snowpack properties[J].Nordic Hydrology,1979,10(1):25-40.

[16]Josberger E G,Mognard N M.A passive microwave snow depth algorithm with a proxy for snow metamorphism[J].Hydrological Processes,2002,16(8):1557-1568.

[17]Goodison B E,Walker A E.Use of snow cover derived from satellite passive microwave data as an indicator of climate change[J].Annals of Glaciology,1993,17:137-142.

[18]Chang A T C,Foster J L,Hall D K.NIMBUS-7 SMMR derived global snow cover parameters[J].Annals of Glaciology,1987,9:39-44.

[19]Tedesco M,Pulliainen J,Takala,et al.Artificial neural network-based techniques for the retrieval of SWE and snow depth from SSM/I data[J].Remote Sensing of Environment,2004,90(1):76-85.

[20]Kelly R.The AMSR-E snow depth algorithm:Description and initial results[J].Journal of the Remote Sensing Society of Japan,2009,29(1):307-317.

[21]孙知文,施建成,杨虎,等.风云三号微波成像仪积雪参数反演算法初步研究[J].遥感技术与应用,2007,22(2):264-267. Sun Z W,Shi J C,Yang H,et al.A study on snow depth estimating and snow water equivalent algorithm for FY-3 MWRI[J].Remote Sensing Technology and Application,2007,22(2):264-267.

[22]Ulaby F T,Moore R K,Fung A K.Microwave Remote Sensing:Active and Passive.Volume I:Microwave Remote Sensing Fundamentals and Radiometry[M].Reading,Massachusetts:Addison-Wesley,Advanced Book Program,1981:1-456.

[23]England A W.Thermal microwave emission from a scattering layer[J].Journal of Geophysical Research,1975,80(32):4484-4496.

[24]Pulliainen J T,Grandell J,Hallikainen M T.HUT snow emission model and its applicability to snow water equivalent retrieval[J].IEEE Transactions on Geoscience and Remote Sensing,1999,37(3):1378-1390.

[25]Wiesmann A,Mätzler C.Microwave emission model of layered snowpacks[J].Remote Sensing of Environment,1999,70(3):307-316.

[26]Tsang L.Dense media radiative transfer theory for dense discrete random media with spherical particles of multiple sizes and permittivities[J].Progress in Electromagnetics Research,1992,5(6):181-230.

[27]Tsang L,Chen C T,Chang A T C,et al.Dense media radiative transfer theory based on quasicrystalline approximation with applications to passive microwave remote sensing of snow[J].Radio Science,2000,35(3):731-749.

[28]Fung A K.Microwave Scattering and Emission Models and Their Applications[M].Boston:Artech House,1994:1-573.

[29]Armstrong R L,Rango A,Chang A T C,et al.Snow depths and grain size relationships with relevance for passive microwave studies[J].Annals of Glaciology,1993,17:171-176.

[30]Chang A T C,GIoersen P,Schmugge T,et al.Microwave emission from snow and glacier ice[J].Journal of Glaciology,1976,16(74):23-39.

[31]Langlois A,Royer A,Dupont F,et al.Improved corrections of forest effects on passive microwave satellite remote sensing of snow over boreal and subarctic regions[J].IEEE Transactions on Geoscience and Remote Sensing,2011,49(10):3824-3837.

[32]Sturm M,Holmgren J,Liston G E.A seasonal snow cover classification system for local to global applications[J].Journal of Climate,1995,8(5):1261-1283.

[33]Kelly R E,Chang A T,Tsang L,et al.A prototype AMSR-E global snow area and snow depth algorithm[J].IEEE Transactions on Geoscience and Remote Sensing,2003,41(2):230-242.

[34]Grippa M,Mognard N,Toan T L,et al.Siberia snow depth climatology derived from SSM/I data using a combined dynamic and static algorithm[J].Remote Sensing of Environment,2004,93(1-2):30-41.

[35]Goodison B,Walker A.Canadian development and use of snow cover information from passive microwave satellite data[M]//Choudhury B,Kerr Y H,Njoku E G,et al.Passive Microwave Remote Sensing of Land-Atmosphere Interactions.Utrecht:VSP International Science Publishers,1995:245-262.

[36]Davis D T,Chen Z X,Tsang L,et al.Retrieval of snow parameters by iterative inversion of a neural network[J].IEEE Transactions on Geoscience and Remote Sensing,1993,31(4):842-852.

[37]Durand M,Liu D S.The need for prior information in characterizing snow water equivalent from microwave brightness temperatures[J].Remote Sensing of Environment,2012,126:248-257.

[38]杨虎,郭华东,王长林,等.基于神经网络方法的极化雷达地表参数反演[J].遥感学报,2002,6(6):451-455. Yang H,Guo H D,Wang C L,et al.Polarimetric SAR surface parameters inversion based on neural network[J].Journal of Remote Sensing,2002,6(6):451-455.

[39]孙知文.风云三号微波成像仪(FY-3 MWRI)积雪参数反演算法研究与系统开发[D].北京:北京师范大学,2007. Sun Z W.Estimate Snow Depth and Snow Water Equivalent Algorithm for FY-3 MWRI and Development of System[D].Beijing:Beijing Normal University,2007.

[40]Chang A T C,Rango A.Algorithm Theoretic Basis Document(ATBD) for the AMSR-E Snow Water Equivalent Algorithm,Version 3.1[R].USA:NASA,2000.

[41]杨虎,李小青,游然,等.风云三号微波成像仪定标精度评价及业务产品介绍[J].气象科技进展,2013,3(4):136-143. Yang H,Li X Q,You R,et al.Environmental data records from Feng Yun-3B mircowave radiation imager[J].Advances in Meteorological Science and Technology,2013,3(4):136-143.

[42]Hallikainen M T,Ulaby F,Abdelrazik M.Dielectric properties of snow in the 3 to 37 GHz range[J].IEEE Transactions on Antennas and Propagation,1986,34(11):1329-1340.

(责任编辑： 刘心季)

Progress in study of snow parameter inversion by passive microwave remote sensing

SUN Zhiwen1， YU Pengshan2， XIA Lang3， WU Shengli4， JIANG Lingmei5， GUO Lei1

(1.SpaceStarTechnologyCo.，Ltd. ,Beijing100086，China；2.BeijingShenzhouAerospaceSoftwareTechnologyCo.,Ltd.,Beijing100094,China; 3.KeyLaboratoryofResourceRemoteSensingandDigitalAgriculture，Beijing100081，China；4.NationalSatelliteMeteorologicalCenter，Beijing100081，China；5.StateKeyLaboratoryofRemoteSensingScience，BeijingNormalUniversity，Beijing100875，China)

Snow depth(SD)and snow water equivalent(SWE)are key parameters in hydrology and climate research，especially in the snowstorm monitoring. In this paper，the authors first provided a brief background of the physical basis of the SD and SWE inversion algorithm，i.e., the snow microwave radiative transfer model，and discussed the snow microwave radiation and scattering in different microwave frequencies. After that, the former snow estimation inversion algorithms were reviewed, which can be categorized into two types: linear brightness temperature gradient and prior knowledge-based from mathematical methods. The advantages and limitations of the two algorithms were summarized. The linear brightness temperature gradient method is easier and runs faster，but it only suits specific study areas. For the establishment of a prior knowledge-based model，researchers need to obtain the sample data and repeated training so as to achieve higher accuracy. However, the model requires the independence and significant mean difference of the samples. The SD and SWE inversion algorithms for Fengyun-3 microwave radiation imager (FY-3 MWRI) were described，which are composed of global business algorithm and improved regional algorithm for China. Finally, the research focuses in this aspect were predicted.

passive microwave remote sensing；microwave radiometer；snow depth(SD)；snow water equivalent(SWE)；inversion algorithm

2013-11-05；

2014-01-15

10.6046/gtzyyg.2015.01.02

孙知文，于鹏珊，夏浪，等.被动微波遥感积雪参数反演方法进展[J].国土资源遥感，2015，27(1)：9-15.(Sun Z W，Yu P S，Xia L，et al.Progress in study of snow parameter inversion by passive microwave remote sensing[J].Remote Sensing for Land and Resources，2015，27(1)：9-15.)

TP 79

A

1001-070X(2015)01-0009-07

孙知文(1983-)，男，工程师，主要从事微波遥感、微波辐射定标等方向的研究。Email： sunzhiwen503@163.com。