II／III期无缝设计二分类变量效应的估计*

南京医科大学流行病与卫生统计教研室（210029） 王冠融 邵 方 刘丽亚 陈 峰 柏建岭 于 浩

II／III期无缝设计二分类变量效应的估计*

南京医科大学流行病与卫生统计教研室（210029） 王冠融 邵 方 刘丽亚 陈 峰 柏建岭 于 浩△

目的针对二分类结果变量，探索II／III期无缝设计的效应估计。方法期中分析选择疗效最优的一个试验组进入二阶段，考虑早期无效终止，研究试验进入二阶段条件下的疗效无偏估计。本文基于二分类资料推导出疗效的一致最小方差无偏估计法，并比较该法与极大似然估计法及二阶段估计法的偏性和均方误差。结果就偏性而言，二阶段估计法最小，极大似然估计法最大，一致最小方差无偏估计法稍高于二阶段估计法；就均方误差而言，极大似然估计法最小，二阶段估计法最大，一致最小方差无偏估计法稍高于极大似然估计法。结论针对二分类资料，一致最小方差无偏估计法的偏性及均方误差相对较小，在可接受范围内，故推荐该法作为二分类资料无缝设计的效应估计方法。

II／III期无缝设计 二分类资料 效应估计 一致最小方差无偏估计法

近几年，由于II／III期无缝设计可以节约研发时间和成本而被大家广泛关注［1－2］。无缝设计根据一阶段的结果指导期中分析决策，判定试验是否进入下一个阶段，若试验可以继续，则筛选出最有前途的试验组（或剂量组），与对照组一起进入二阶段，试验完成后进行最后分析［3］。II／III期无缝设计在确证性分析时也利用了探索阶段的数据，因此它是一种高效率的设计，但同时也给统计推断带来许多挑战［4］。目前，人们关注较多的是如何进行有效的组别筛选，并控制好整个试验的I类错误，对点估计这一统计学性质关注较少。本研究关注于如何综合两阶段的数据对药物疗效进行无偏估计。

由于期中分析一般选择估计疗效最好的处理组进入下一阶段研究，因此无缝设计的效应估计结果往往会超过实际的效应值。目前，Cohen等［5］对无缝设计效应估计进行研究，并提出一致最小方差条件无偏估计方法。Peter等［2］与Bowden等［6］学者对上述方法针对定量结果变量进行了更深层次的研究。本文针对二分类资料，推导出一致最小方差无偏估计的公式，并与其他方法进行比较。

原理与方法

根据观察到的两个阶段的数据估计药物疗效。假定期中分析时选择疗效最优组进入下一阶段研究，考虑早期无效终止的情形。以有效率为终点指标，本文考虑一阶段试验组数为k（≥2）个，对照组数为1个，并假设同一阶段每组样本量相同，第一阶段样本量记为nI，第二阶段样本量记为nII。假定第i（i＝0，1，…，k）组有效人数服从B（ni，πi），i＝0表示对照组。一阶段样本有效率记为pIi。将选择出的试验组记为S（S∈｛1，…，k｝），S与对照组同时进入二阶段，二阶段各组有效人数服从B（nII，πi）。根据二阶段样本得到的有效率记为pIIi。提前终止试验标准为：一阶段结束时若pIS－pI0≤b0，则试验无效终止，这里b0称作无效界值。本研究的目的是试验结束后对两组真实有效率差Δs＝πs－π0进行估计。

1．极大似然估计法（maximum likelihood，MLE）

我们将nI／（nI＋nII）记作期中分析信息时间t，试验完成后根据样本得到对照组的有效率为p0，MLE＝tpI0＋（1－t）pII0，筛选组有效率为ps，MLE＝tpIS＋（1－t）pIIS，此时利用筛选组与对照组的极大似然估计，可以得到两组的率差估计公式如下：

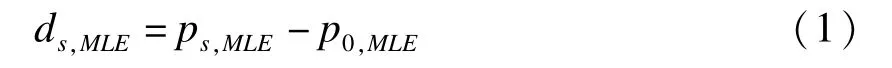
由于选择疗效估计最大的试验组进入下一阶段研究，故这种估计方法往往会高估疗效。

2．二阶段估计法（stage 2 estimator）

若疗效估计以试验继续进入二阶段为条件，那么pII0和pIIS就是π0和πS的无偏估计，此时两组率差为

公式（2）是Δs的无偏估计，称作二阶段估计方法。此法虽然无偏，但是只利用了二阶段的数据，因此不够稳定。

3．一致最小方差无偏估计法（uniform ly minimum variance unbiased estimation，UMVUE）

本文基于Rao-Blackwell定理，推导出基于二分类资料的一致最小方差无偏估计（UMVUE）方法。Rao-Blackwell定理是以一个无偏估计为起点，寻找其最小方差无偏估计量。无论真实参数值是多少，最小方差无偏估计都比其他无偏估计有更小或至多相等的方差。由上述可知，pIIS是πS的无偏估计，根据Rao-Blackwell定理，pIIS的条件期望就是πS的最小方差无偏估计。同理，pII0的条件期望就是π0的无偏估计。一阶段结束后对各试验组疗效排序，记为pI（1）＞pI（2）＞…＞pI（k），其中pIS＝pII（1）。对于筛选组，用pS，MVE表示疗效的一致最小方差无偏估计，根据推导，得到的公式如下：

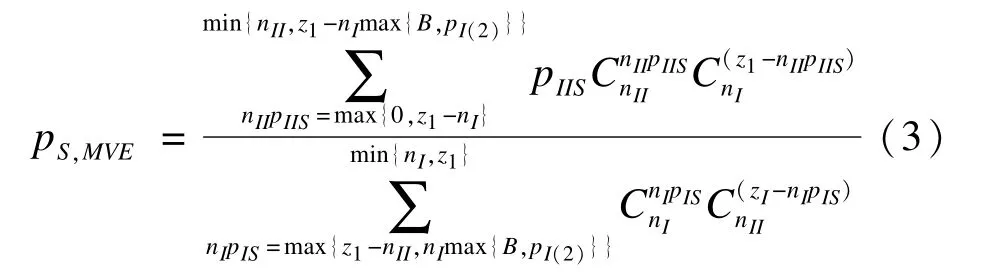
用p0，MVE表示对照组的疗效一致最小方差无偏估计，根据推导，得到的公式如下：

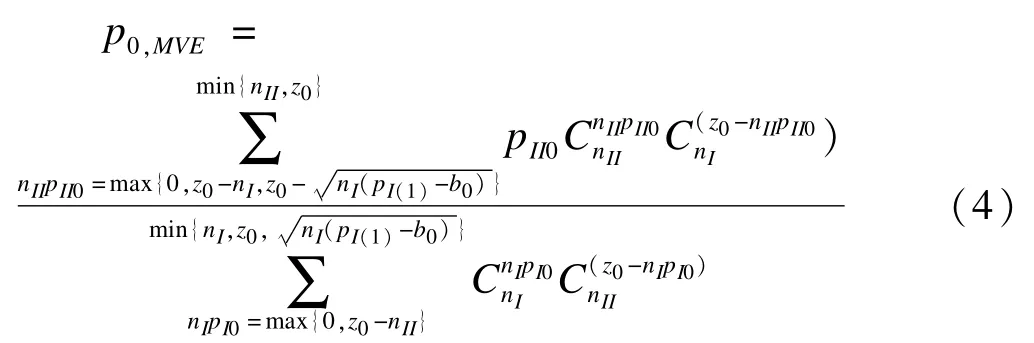
其中，z1＝nIpIS＋nIIpIIS，z0＝nIpI0＋nIIpII0，B＝b0＋pI0。由于pS，MVE，p0，MVE分别是πS和π0的无偏估计，那么ΔS的无偏估计为

模拟试验

根据Stallard和Todd［7］的研究，极大似然估计法的偏性取决于处理组数k，期中分析时间点t，无效界值b0，筛选组与对照组的真实率差ΔS。故本文考察以下几种参数设置对偏性（bias）和均方误差（rootmean square error，RMSE）的影响。具体参数设置见表1、2。

表1 模拟试验参数含义

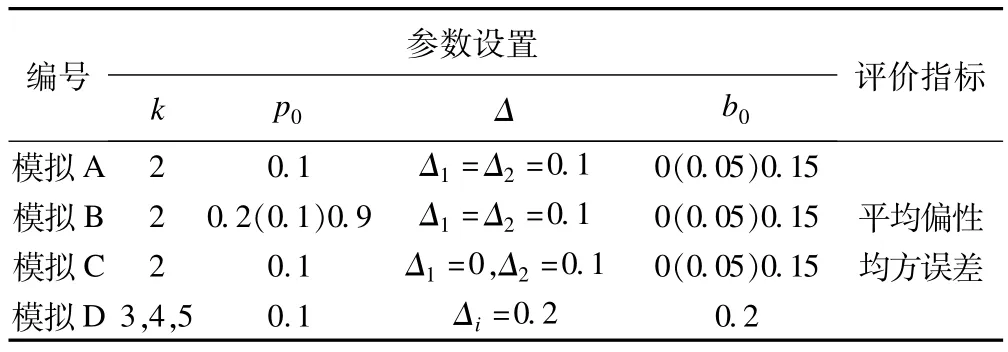
表2 模拟试验设置的基本情况

在上述参数设置下，每一次模拟中，根据公式（1）、（2）、（5）计算分别得到极大似然估计法、二阶段估计法、一致最小方差无偏估计法疗效差别的效应估计。若将估计值统一用dS，est表示，则偏性为Bias＝（dS，est－Δs），对10000次模拟求平均即得到平均偏性；均方误差为

1．模拟A

此种模拟情境设定试验中有两个试验组和一个对照组，两个试验组的效应相同且都为0．2，即Δ1＝Δ2＝0．1。模拟结果见图1、2。

图1 四种无效界值下3种估计方法的偏性，k＝2，Δ1＝Δ2＝0．1

从图1中可以看出，极大似然估计法是偏性的，且随着期中分析信息时间t后移而增加，也随着无效界值b0的增加而增加；二阶段估计法一直都是无偏的，不随t和b0的增加而改变；UMVUE法的偏性在b0较小时控制的很好，几乎可以忽略不计。随着b0增大，UMVUE法的偏性增加，但仍远远低于极大似然法的偏性。从图2前三幅图中可以发现，极大似然估计法的RMSE最小；二阶段估计法的RMSE最大；UMVUE法的RMSE稍高于极大似然法。但当b0＝0．15时，极大似然估计法的RMSE明显增加，二阶段估计法的RMSE依然很大，此时UMVUE法的RMSE最小。这说明极大似然估计法的RMSE容易受无效界值b0的影响，而UMVUE法相对稳定很多。

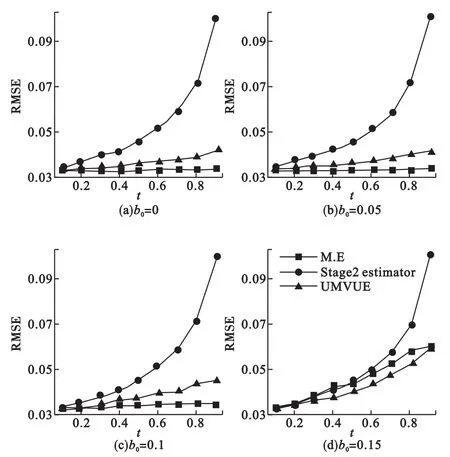
图2 四种无效界值下3种估计方法的RMSE，k＝2，Δ1＝Δ2＝0．1

我们在保持上述四个无效界值b0下，改变Δ1＝Δ2＝0．2，Δ1＝Δ2＝0．3，Δ1＝Δ2＝0．6，结论同前，此处不再列出图形。同时我们发现，极大似然估计的偏性随着Δ的增加而减少，并且当Δ1＝Δ2＝0．6，四种b0取值下极大似然估计的偏性几乎完全相同。这主要是由于每一次模拟处理组效应都超过了无效界值，偏性主要由组别筛选产生，因此极大似然估计的偏性是相同的。

模拟B的结果与模拟A结果几乎相同，p0由0．1增加至0．5时，极大似然估计法的偏性和均方误差都轻微增加（1%以内），p0由0．5增加至0．9时，极大似然估计法的偏性和均方误差都逐渐减小，即p0＝0．5，偏性和均方误差最大。UMVUE法和二阶段估计法的偏性和均方误差几乎不受p0的影响。

2．模拟C

此种模拟情境表示试验中有两个试验组和一个对照组，设定两个试验组的效应不同Δ1＝0，Δ2＝0．1。模拟结果见图3、4。

由图3、图4可知，模拟C的结论与模拟A相似，这里不再赘述。唯一的区别是，当b0取值较小时，偏性不随着期中分析信息时间t的后移而增加，这是由于当两组差别不等时，随着t的增加，选错组别的机会减少，因此偏性减少。

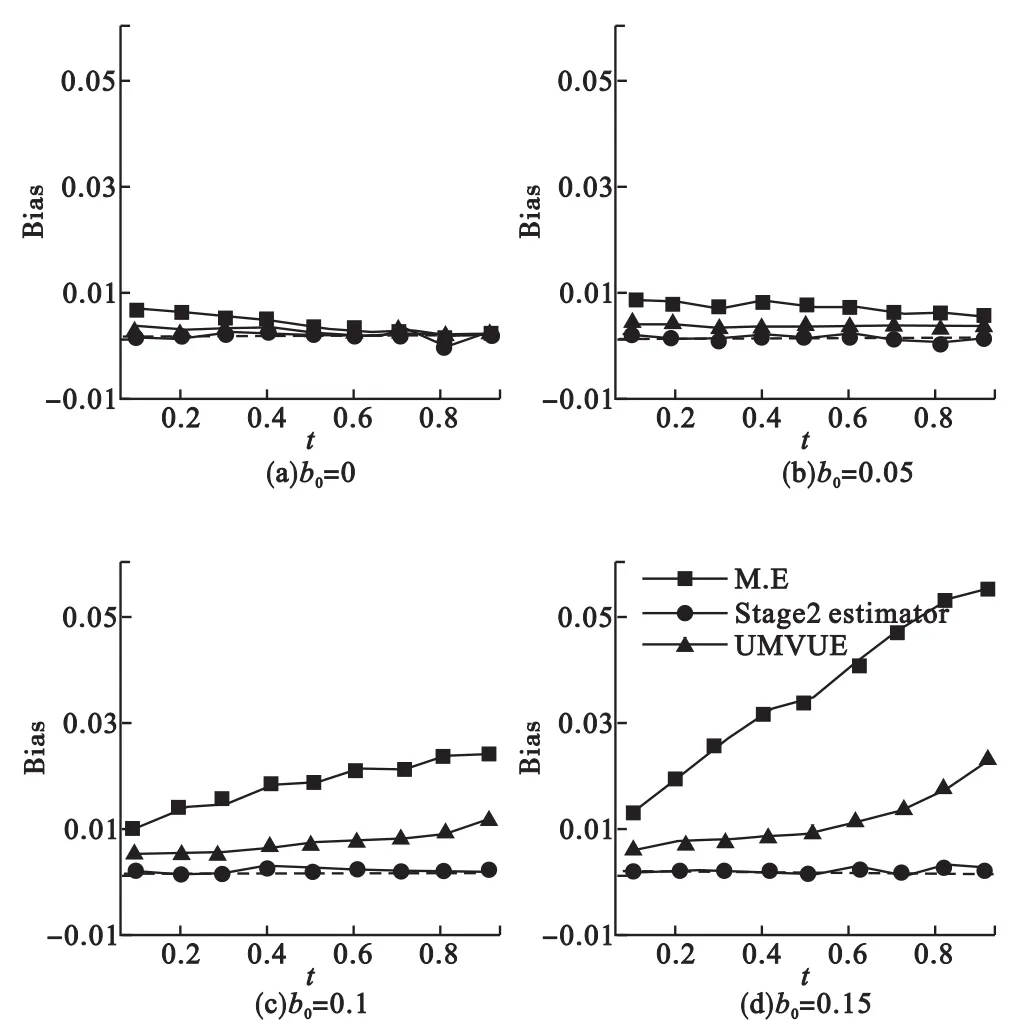
图3 四种无效界值下3种估计方法的偏性，k＝2，Δ1＝0，Δ2＝0．1

3．模拟D

我们模拟了k取3，4，5的情形，一般结果同上，这里不再列出。图5显示了k对各方法的偏性和均方误差的影响。

由图5可见，随着k的增加，极大似然估计法的偏性和均方误差都轻微增加，而二阶段估计法和UMVUE估计法基本不受k的影响。

实例分析

实例为一项关于艾迪康唑乳膏治疗足癣的多中心、随机、双盲、阳性药物平行对照的临床试验。其研究目的是探索最佳给药浓度，主要效应指标为停药2周后真菌清除率。其中，一阶段样本量为72，二阶段样本量为120，因此期中分析信息时间t＝0．375。我们只利用部分的研究数据（见表3），介绍如何使用3种效应估计方法。

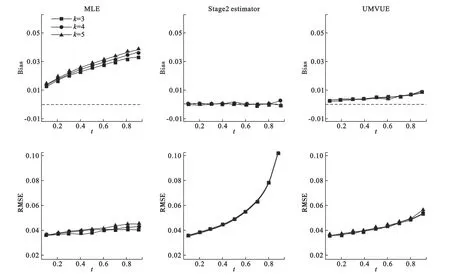
图5 3种估计方法的偏性和均方误差与组数k的关系，Δ1＝Δ2＝0．2，b0＝0．2

表3 各组足癣病人停药后2周真菌清除率

我们设定当一阶段筛选组与对照组疗效差别大于0时，则试验继续进入二阶段，即无效界值b0＝0。根据表3中的数据，计算得到p0，MLE＝0．8056×0．375＋0．8235×0．625＝81．68%，pS，MLE＝0．9028×0．375＋0．8914×0．625＝89．57%，此时用极大似然估计效应差别为7．89%；直接用二阶段估计法得到效应差别为6．79%；B＝0＋0．8056＝0．8056，

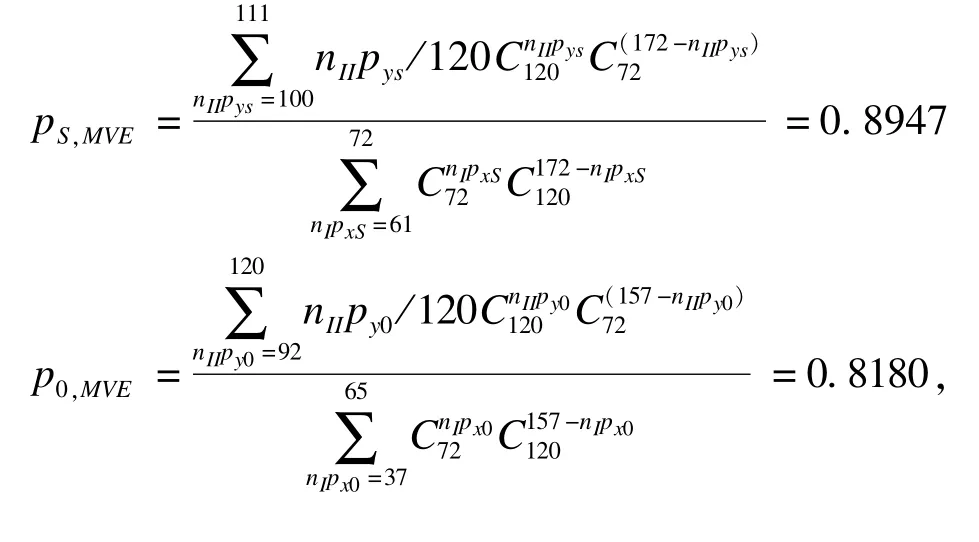
因此用一致最小方差无偏估计法估计的效应差别为7．67%。

讨 论

在药物研发过程中，缩短研发时间和降低研发成本的需求促使了适应性无缝设计的出现。适应性无缝设计将一个临床试验分为几个阶段逐步实施，与传统方法相比，统计学面临了许多新的挑战。Cohen和Sackrow itz［5］、Shen［8］针对定量资料研究了试验总是进入二阶段条件下效应的无偏估计，Stallard和Todd［7］在2005年也提出一种针对上述条件的无偏估计法，Peter K等人［2］对上述方法进行扩展，使其可用于早期无效终止的情形。本文针对二分类资料，以II／III期无缝设计为例，在期中分析时选取疗效最优的组别与对照组同时进入第二阶段，其中考虑早期无效终止，研究试验进入二阶段条件下的效应估计。

本文针对有效率为终点指标的情形，推导出试验效应的一致最小方差无偏估计，并评价其偏性和均方误差。该法基于Arthur Cohen和Harold B［4］给出的联合密度函数，根据Rao-Blackwell定理推导而得。模拟试验结果表明，极大似然估计法的偏性最大，二阶段估计法在任何条件下都是无偏的，一致最小方差无偏估计法的偏性稍高于二阶段估计法；二阶段估计法的均方误差最大，极大似然估计法的均方误差在无效界值较小时均方误差最小，当无效界值较大时极大似然估计法的均方误差明显增加，一致最小方差无偏估计法的均方误差稍高于极大似然估计法，且当无效界值较大时，一致最小方差无偏估计的均方误差最小。Arthur Cohen和Harold B［4］给出的联合密度函数针对定量资料（正态分布），定性资料（二项分布）在阳性数足够大时近似正态，在此方法的基础上扩展应用时具有一定的偏性，与模拟试验结果契合。

监管机构要求在对疗效进行点估计和区间估计时必须控制好I类错误［9］，并强调需要控制点估计的偏性［10］，综合上述三种方法，一致最小方差无偏估计法的偏性和均方误差均较小，在可接受范围内，故推荐使用该法作为二分类资料无缝设计的效应估计方法。可信区间提供效应估计的同时也提供了假设检验方面的信息，Shen在2001年提出针对二分类数据构造II／III期无缝设计可信区间的方法［8］。而基于本研究介绍的效应点估计原理构建各试验组的可信区间是一个待研究的问题。

［1］吴莹，侯艳，李康．适应性无缝设计在临床试验中的应用及研究进展．中国卫生统计，2013，30（1）：140-142．

［2］Peter K，Kimani，Susan Todd，etal．Conditionally unbiased estimation in phase II／III clinical trials with early stopping for futility．Statistics in Medicine，2013，32：2893-2910．

［3］Frank B，Heinz S，Franz K，et al．Confirmatory seam less phase II／III clinical trials with hypotheses selection at interim：general concepts．Biometrical Journal，2006，48（4）：623-634．

［4］Shein Chung Chow，Ralph Corey．Benefits，challenges and obstacles of adaptive clinical trial designs．Orphanet Journal of Rare Diseases，2011，6：79．

［5］Arthur Cohen，Sackrow itz HB．Two stage conditionally unbiased estimators of the selected mean．Statistics＆Probability Letters，1989，8：273-278．

［6］Jack Bowden，Ekkehard Glimm．Unbiased Estimation of selected treatmentmeans in two-stage trials．Biometrical Journal，2008，4：515-527．

［7］Stallard N，Todd S．Point estimates and confidence regions for sequential trials involving selection．Journal of Statistical Planning and Inference，2005，135：402-419．

［8］Shen L．Estimation follow ing selection of the largestof two normal means．Statistics in Medicine，2001，20：1913-1929．

［9］Food and Drug Adm inistration．Guidance for industry：adaptive design clinical trials for drugs and biologics＠ONLINE，11 February 2013．（Available from：http：／／www．fda．gov／downloads／Drugs／Guidance-ComplianceRegulatory Information／Guidances／UCM 201790．pdf）

［10］Chmp，Emea．Reflection paper onmethodological issues in confirmatory clinical trials planned with an adaptive design＠ONLINE，11 February 2013．（Available from：http：／／www．ema．europa．eu／docs／en＿GB／document＿library／Scientific＿guideline／2009／09／WC500003616．pdf）10

（责任编辑：郭海强）

Point Estimator in Seam less Phase II／IIIClinical Trials for Binary Data

Wang Guanrong，Shao Fang，Liu Liya，etal．（DepartmentofEpidemiology＆Biostatistics，NanjingMedicalUniversity（210029），Nanjing）

ObjectiveTo explore unbiased estimation of effects in seam less phase II／IIIdesign particularly for qualitative data．MethodsWe consider pointestimation of the treatmenteffect in which stage 1 is used to select themosteffective experimental group and to decide whether the trial should stop at stage 1 futility by comparing with the control group．We have developed a new estimator for the treatment difference，and compared it with other estimators by simulations．ResultsOn the whole，for biases，stage 2 estimator is an unbiased method；themaximum likelihood estimator always over-estimates；and the bias of the UMVUE is slightly higher than the stage 2 estimator．For MSE，the stage 2 estimator performsworst，while themaximum likelihood estimator performs best，and the UMVUE performs slightly better than themaximum likelihood estimator．ConclusionBased on binary data，the bias and MSE of the UMVUE are relatively small，within the acceptable range．Therefore，we recommend it as the point estimator of the treatment effect in seam less phase II／III clinical trials．

Seam less phase II／III clinical trials；Binary data；Estimation；UMVUE

*：国家自然科学基金（81273184）；国家自然科学青年基金（81302512）

△通信作者：于浩，E-mail：haoyu＠njmu．edu．cn