基于GA-BP网络的LFM信号脉冲压缩*

杨宁国，任新涛

(中国人民解放军63863部队，吉林 白城　137001)



基于GA-BP网络的LFM信号脉冲压缩*

杨宁国，任新涛

(中国人民解放军63863部队，吉林 白城137001)

摘要：为了改善线性调频 (linear frequency modulation，LFM) 信号脉冲压缩输出的性能，研究了误差反向传播(back propagation，BP)神经网络在线性调频信号脉冲压缩中的应用。采用遗传算法(genetic algorithm，GA)对BP神经网络的连接权值进行训练学习，该算法可克服BP网络容易陷入局部最优的缺点。仿真结果表明，GA-BP网络具有较快的收敛速度和较好的数值稳定性，在信噪比损失小于1 dB的条件下，可获得60 dB左右的输出主旁瓣比。

关键词：线性调频信号；脉冲压缩；遗传算法；GA-BP网络；主旁瓣比

0引言

现有雷达的发射信号大多采用大时带积的LFM(linear frequency modulation)信号和相位编码信号。为了提高作用距离、改善距离分辨率及抗干扰能力，雷达普遍采用脉冲压缩技术。LFM信号脉冲压缩时，为了抑制旁瓣电平，通常会在匹配滤波器后级联一个旁瓣抑制滤波器，构成一个失配滤波器。最具代表的有Ackroyd提出的基于积累旁瓣电平(integrated side-lobe level，ISL)最小的最小均方逆滤波法和Zoraster提出的基于峰值旁瓣电平(peak side-lobe level，PSL)最小的线性规划法[1]。旁瓣抑制滤波器的设计其实是在多个脉压输出指标之间折中取优的过程，付出的代价是信噪比损失和分辨力下降，而且滤波器的形式不具备可以灵活调节的参数(如Hanmming窗等)，或者虽然有可调节的参数，但是参数本身不具备明确的物理意义(如Taylor窗等)[2]。

20世纪90年代以后，学者们开始将神经网络技术应用于脉冲压缩的研究[3]，以便提高脉压的智能化水平，获得更好的效果。本文针对LFM信号，研究BP(back propagation)神经网络在其脉冲压缩中的应用，采用GA(genetic algorithm)算法对BP神经网络的权值进行训练学习，能够提高神经网络的收敛速度和学习能力，有效克服了网络容易陷入局部最优的缺点，并通过仿真验证了网络的能力。

1脉压输出信号的性能指标

设雷达的视频回波序列s(n)与失配滤波器系数序列h(n)进行脉冲压缩后的输出序列为{y1,y2,…,yn-1,yn,yn+1,…,y2n-1}，其中yn为期望的输出，其余都是不需要的旁瓣。对失配滤波器脉压输出信号的性能常用以下3个指标进行衡量。

(1) PSL

PSL是衡量脉压后输出信号最大旁瓣和峰值主瓣的比值[4-5]。

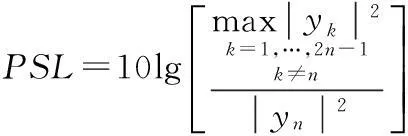
(2) ISL

ISL是衡量脉压后输出信号旁瓣能量和峰值主瓣能量的比值。

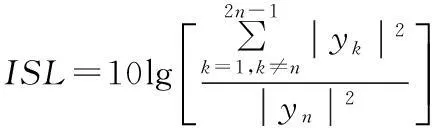
(3) 信噪比损失(signal-to-noise ratio loss,SNRL)

SNRL是衡量失配滤波器导致的信噪比损失[5-6]。

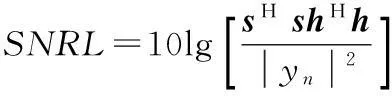
式中：信号序列s=(s1,s2,…,sn)T；失配滤波器序列h=(h1,h2,…,hn)T，上标T和H分别表示转置和共轭转置。

2基于GA-BP算法的失配滤波器设计

GA算法作为一种智能的全局搜索算法，将它应用于BP神经网络权值的训练学习，能克服BP神经网络算法中学习效率低、收敛速度慢、容易陷入局部最优等缺点。

应用GA-BP神经网络对线性调频信号进行脉冲压缩处理，输入向量前向传播，输出向量与期望响应的误差在迭代训练中不断从后向前反向传播。在传播过程中，应用GA算法逐层优化网络的权值和偏差，直到输出最优脉压结果。基于GA-BP算法的失配滤波器的结构框图如图1所示[7-8]。

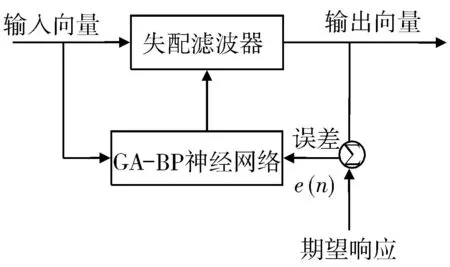
图1　失配滤波器结构框图Fig.1　Structure diagram of mismatched filter

GA-BP神经网络采用通用的三层结构。输入层神经元个数为视频回波序列s=(s1,s2,…,sn)的长度n。选择一层隐含层，为了恰当的检测，隐含层至少需要2个神经元，考虑到网络的鲁棒性，在隐含层中至少还需要1个神经元，所以隐含层设置为3个神经元。输出层神经元的个数为1个[3]。

网络的训练样本由回波序列s的转置sT循环移位所得[9]。

网络的期望输出为T=(0,0,…,1,…,0,0)，其中T的长度为l=2n-1，期望有用的结果1的位置在k=(l+1)/2处。

2.1GA算法[10-11]

GA算法是通过模拟自然界中生物的遗传进化过程，形成的一种全局自适应优化概率搜索算法。GA算法对最优解的搜索过程，是通过所谓的遗传算子作用于群体P(t)中，反复进行遗传操作，得到具有最大适应度群体的过程。GA算法的流程图如图2所示。

图2　GA算法的流程图Fig.2　GA flow chart

GA算法的运算步骤为

(1) 初始化

设置进化代数计数器t=0,设置最大进化代数T，随机生成M个个体作为初始化群体P(t)。

(2) 个体评价

计算群体P(t)中个体适应度。

(3) 选择

根据个体的适应度，按照一定的规则，从群体P(t)中选择出一些优良的个体遗传到下一代群体P(t+1)中。

(4) 交叉

将群体P(t)中的个体随机配对，对每一个个体，以交叉概率交换它们之间的染色体。

(5) 变异

将变异算子作用于群体P(t)，得到下一代群体P(t+1)。

(6) 结束条件

若t≤T，则t=t+1，转到步骤(2)。若t>T，则以进化过程中得到的具有最大适应度的个体作为最优解输出，终止计算。

2.2基于GA算法的BP神经网络优化算法

对一个三层BP神经网络，设Ik为第k个输入节点的输出；Hk为隐含层中第k个节点的输出；Ok为第k个输出节点的输出；WIHij为第i个输入节点与隐含层第j个节点的连接权值；WHOjk为隐含层第j个节点与第k个输出节点的连接权值。则基于GA算法的BP神经网络优化算法步骤为：

(1) 初始化

包括交叉规模、交叉概率、突变概率以及对任一WIHij和WHOjk初始化。

(2) 个体评价

计算每个个体的评价函数，按照下式概率值选择网络个体。

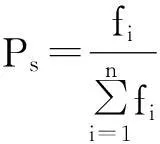
式中：i=1,2,…,n为染色体数；fi=1/E(i)为个体的适配值；E(i)为误差平方和。

(3) 交叉

以交叉概率对个体进行交叉操作产生新个体，没有进行交叉操作的个体直接进行复制。

(4) 变异

利用突变概率对个体进行处理，得到新个体。

(5) BP网络连接权值确定

在迭代范围内，如果找到了满意的个体，则终止，否则转到步骤(2)。超出迭代范围，则将进化过程中得到群体中的最优个体解码，即可得到优化后的网络连接权值。

3仿真结果

为了验证GA-BP神经网络在LFM信号脉冲压缩中的性能，在仿真时，将LFM信号匹配滤波输出结果、加汉明窗后输出结果和采用GA-BP神经网络输出结果进行对比。系统的部分仿真参数设置为：脉冲宽度τ=0.8 μs，采样频率fs=300 MHz，调频带宽B=100 MHz。在不加噪声和多普勒频移时，匹配滤波器的输出如图3所示，加汉明窗的脉冲压缩输出结果如图4所示。

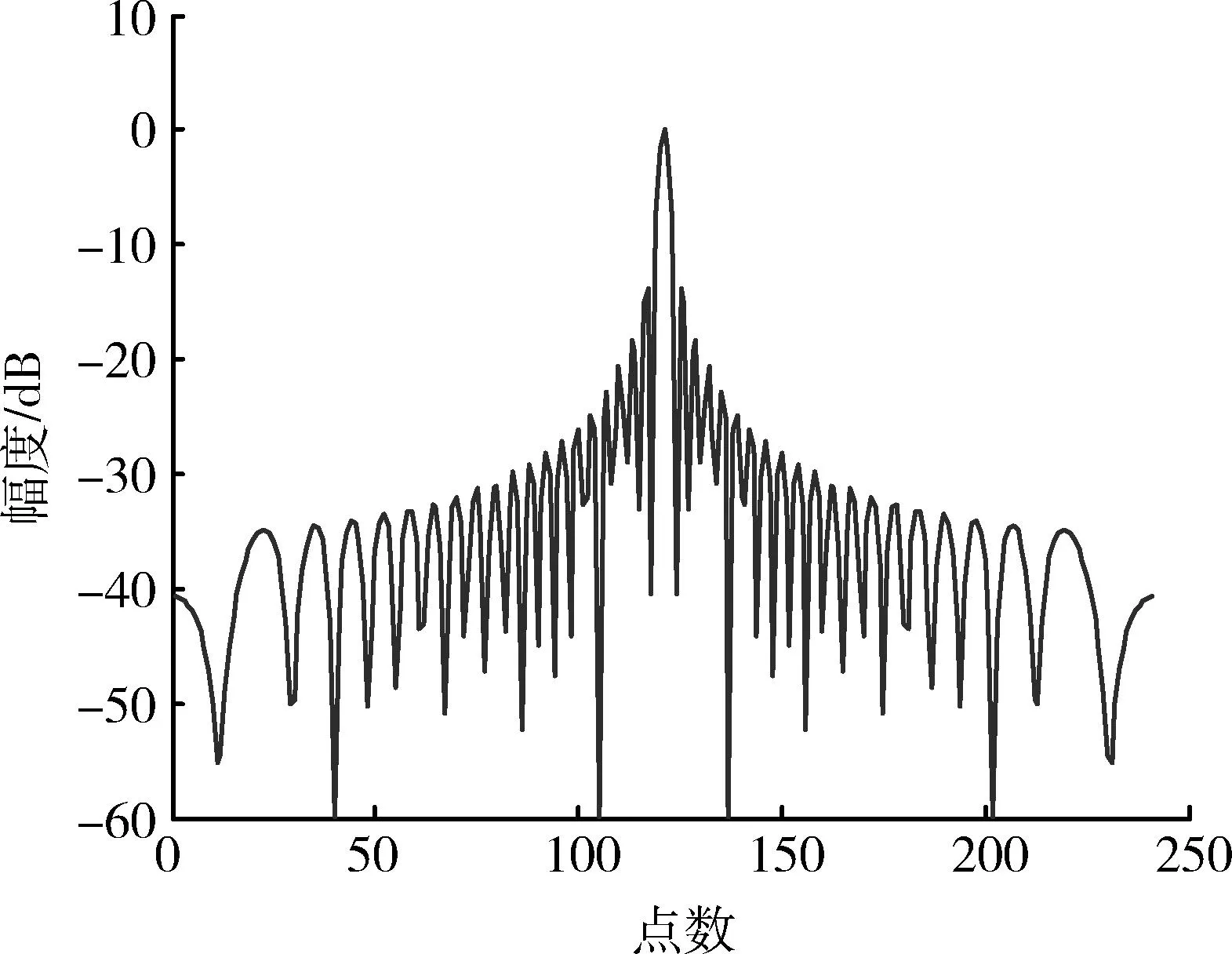
图3　匹配滤波脉压输出结果Fig.3　Matched filter pulse compression output result

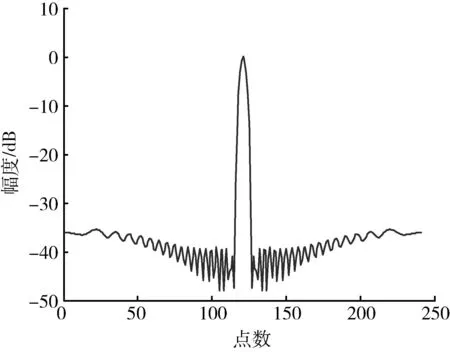
图4　加窗滤波脉压输出结果Fig.4　Windowed filter pulse compression　　　output result

一般雷达的旁瓣峰均值比达到30 dB以上即可满足要求，但有些雷达对旁瓣电平有更高的要求。如航空交通管制系统要求旁瓣电平高于55 dB，星载测雨雷达要求旁瓣电平高于60 dB[12]。从以上2图可以看出，直接进行匹配滤波处理的脉压输出信号的最大旁瓣为-13.2 dB，难以满足一般雷达的探测需求；而进行加窗处理后的脉压输出信号的最大旁瓣可达-35.5 dB左右，但也只能满足一般雷达的探测需求。图5～7为采用GA-BP神经网络进行脉冲压缩时的GA算法的误差变化曲线、适应度函数变化曲线和BP网络误差性能变化曲线，图8为脉冲压缩的输出结果。

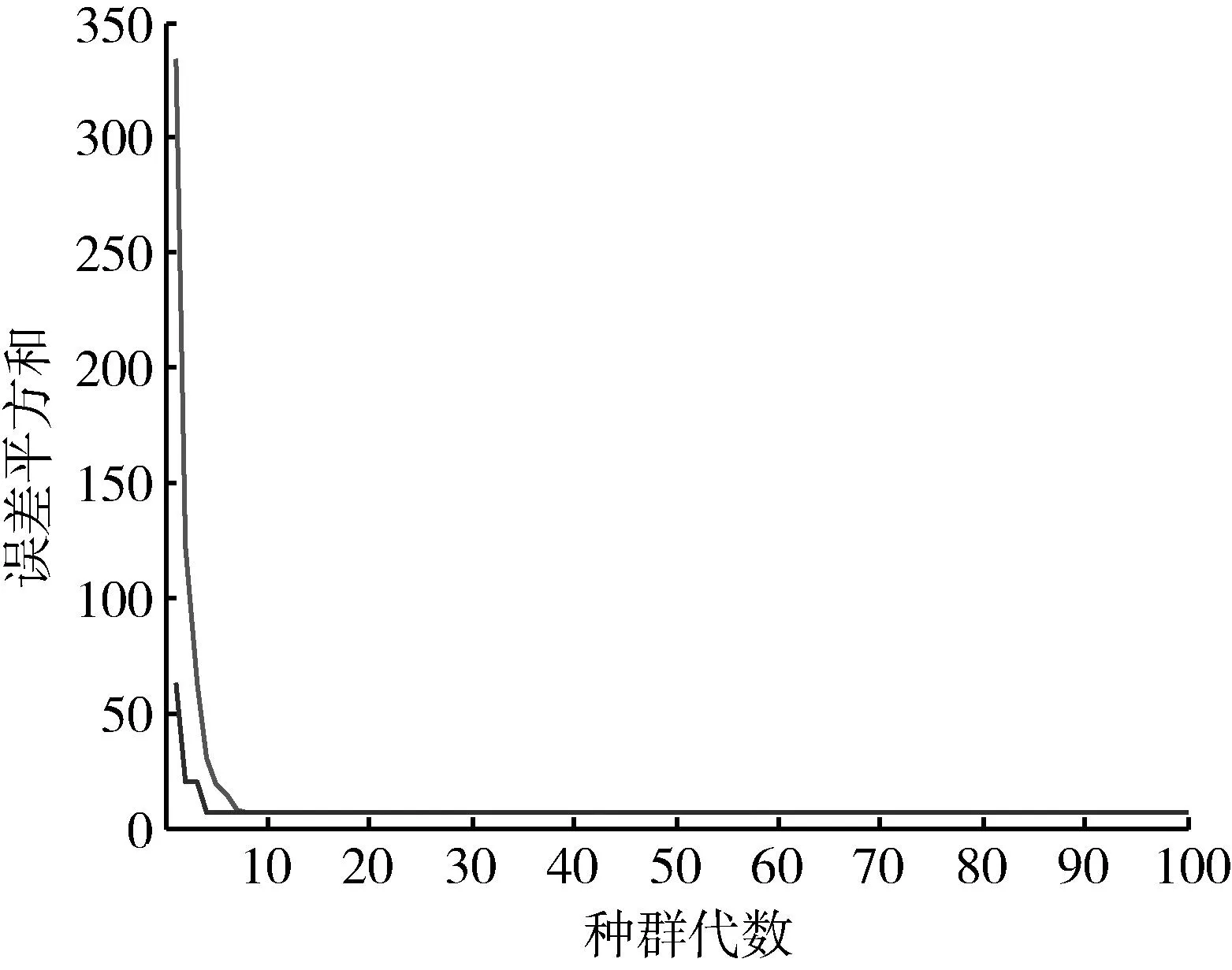
图5　误差变化曲线Fig.5　Error change curve

图6　适应度函数变化曲线Fig.6　Fitness function change curve

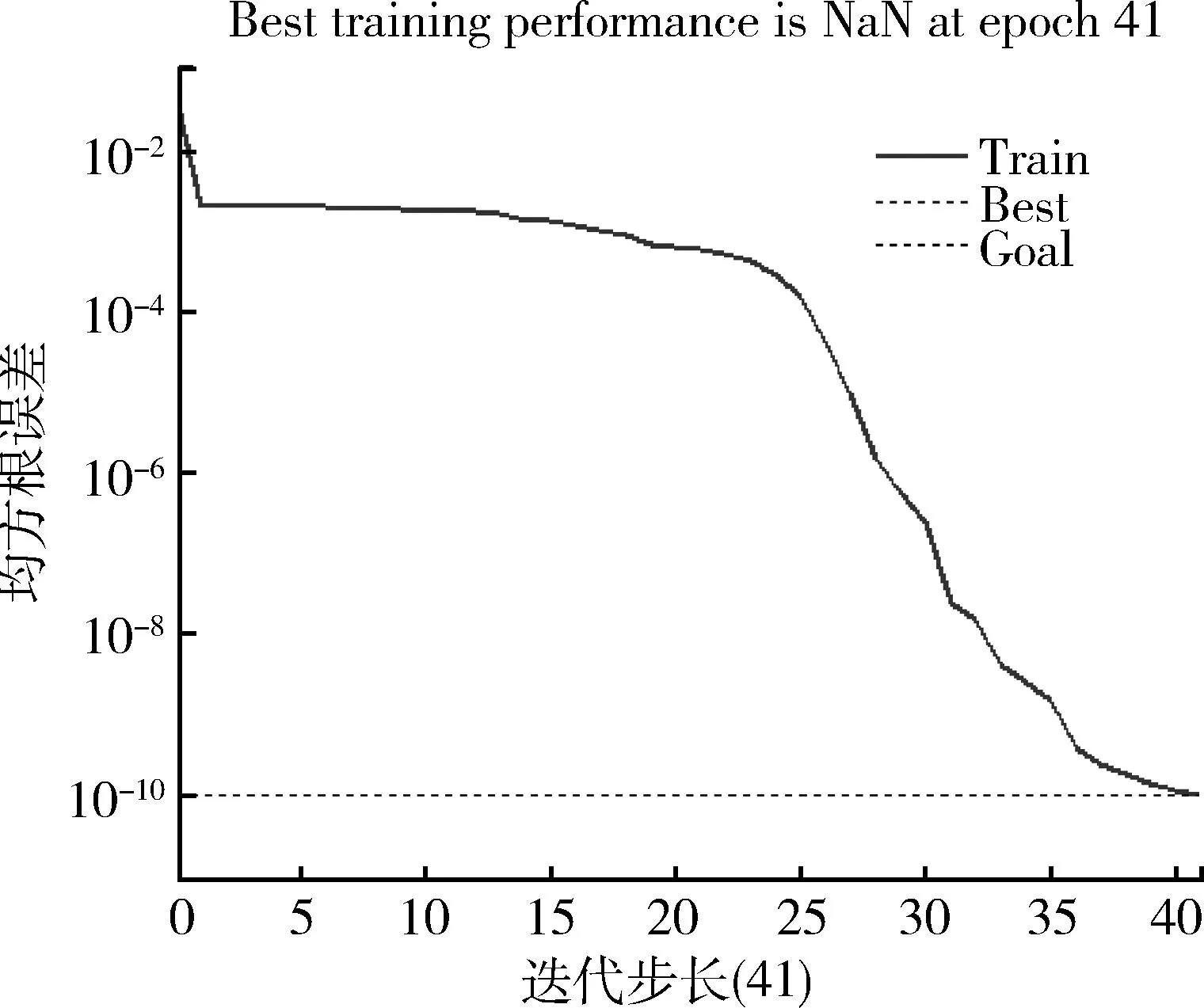
图7　网络误差性能变化曲线Fig.7　Network error performance change curve

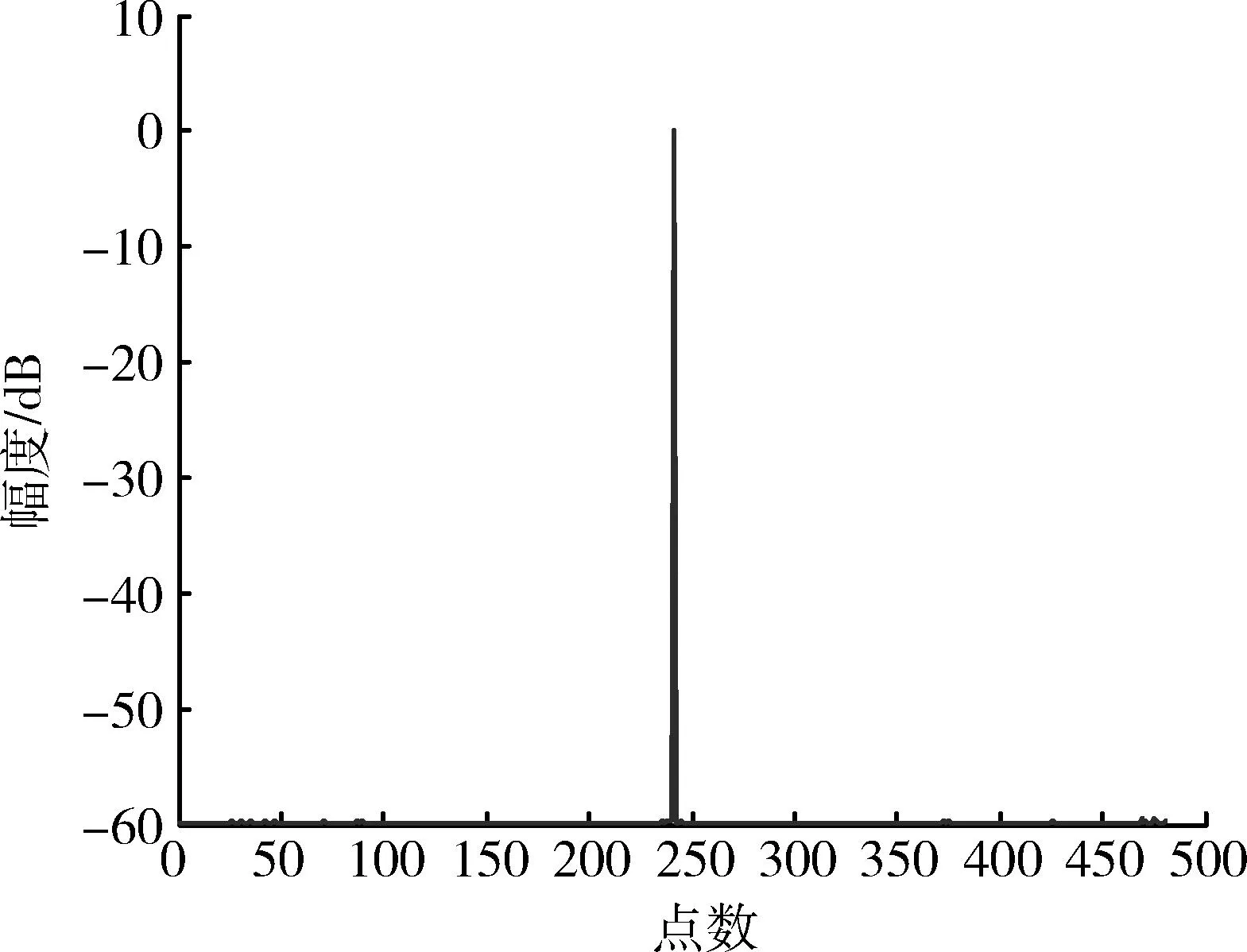
图8　脉冲压缩输出结果Fig.8　Pulse compression output result

从图8可以看出，采用GA-BP神经网络对LFM信号进行脉冲压缩处理，当网络误差目标设置为10-10时，输出的脉压信号最大旁瓣为-60 dB左右，满足了目前大部分雷达的探测需求。表1给出了在不同网络误差目标下，采用GA-BP神经网络脉压输出信号的统计性能指标。

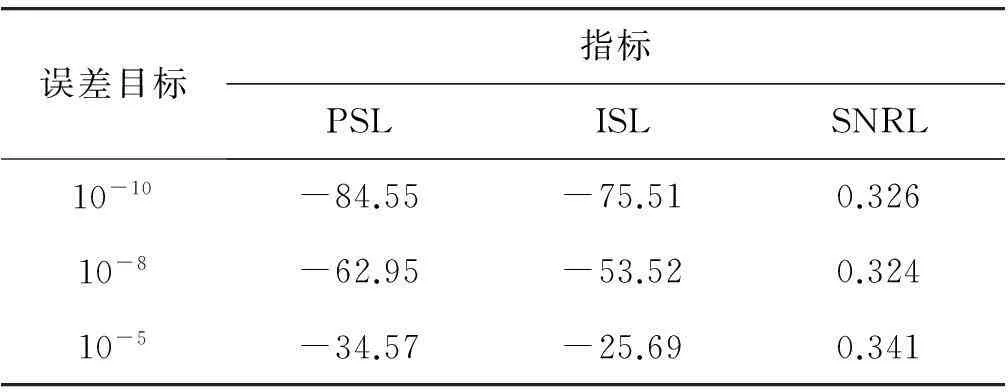
表1　GA-BP神经网络脉压输出信号的统计性能指标

从表1可以看出，在信噪比损失小于1 dB的情况下，采用GA-BP神经网络输出的脉压结果能较好地满足雷达的探测需求。

4结束语

本文将GA算法应用到BP神经网络的权值训练学习中，研究了GA-BP神经网络在LFM信号脉冲压缩中的应用。采用此种方法能克服BP算法中学习效率低、收敛速度慢、容易陷入局部最优等缺点。仿真结果表明，与匹配滤波器和加窗滤波相比，GA-BP神经网路在信噪比损失较小的条件下，能获得较高的脉压输出主旁瓣比。

参考文献：

[1]张仕元, 吴乐南. 基于RLS的脉压雷达数字旁瓣抑制滤波器设计方法[J]. 测控技术, 2006, 25(7): 79-82.

ZHANG Shi-yuan, WU Le-nan. Design of Digital Sidelobe Suppression Filter Based on RLS Method [J]. Measurement & Control Technology, 2006, 25(7): 79-82.

[2]丁淑娟, 刘子龙 孙广俊，等. 线性调频信号数字脉压滤波器优化设计[J]. 数据采集与处理, 2012, 27(5): 602-606.

DING Shu-juan, LIU Zi-long, SUN Guang-jun, et al. Digital Pulse Compression Filter Optimization Design for LFM Signal [J]. Journal of Data Acquisition & Processing, 2012, 27(5): 602-606.

[3]朱志宇, 王建华. RBF神经网络在二相编码雷达脉冲压缩中的应用[J]. 现代雷达, 2005, 27(3): 47-49.

ZHU Zhi-yu, WANG Jian-hua. Application of RBF Neural Network for Pulse Compression in Binary-Code Radar [J]. Modern Radar, 2005, 27(3): 47-49.

[4]郭靖. 基于小波神经网络的多相码雷达信号的旁瓣抑制[D].哈尔滨：哈尔滨工业大学, 2010.

GUO Jing. Sidelobes Suppression for Polyphase-Code Radar Signals Based on Wavelet Neural Network [D].Harbin:Harbin Institute of Technology, 2010.

[5]芮义斌, 魏广雷, 李鹏,等. 长二相码信号旁瓣抑制滤波器的设计[J]. 南京理工大学学报, 2012, 36(4): 685-689.

RUI Yi-bin, WEI Guang-lei, LI Peng, et al. Design of Sidelobe Suppression Filter for Long Biphase-Coded Signals [J]. Journal of Nanjing University of Science and Technology, 2012, 36(4): 685-689.

[6]张仕元, 桂佑林. 低信噪比损失的旁瓣抑制滤波器[J]. 测控技术, 2009, 28(8): 21-24.

ZHANG Shi-yuan, GUI You-lin. Side-Lobe Suppression Filter with Low Loss of Signal-Noise Ratio [J]. Measurement & Control Technology, 2009, 28(8): 21-24.

[7]谭覃燕, 宋耀良. 基于神经网络的混沌调频信号旁瓣抑制算法[J]. 兵工学报, 2010, 31(2): 177-183.

TAN Qin-yan, SONG Yao-liang. Sidelobe Suppression Algorithm for Chaotic FM Signal Based on Neural Network [J]. ACTA Armamentarh, 2010, 31(2): 177-183.

[8]张仕元, 吴乐南. 线性伸缩波形的雷达距离模糊特性及旁瓣抑制[J]. 电子与信息学报, 2006, 28(9):1611-1613.

ZHANG Shi-yuan, WU Le-nan. Radar Range Ambiguity Performance and Sidelobe Suppression of Linear Contracting Waveform [J]. Journal of Electronics & Information Technology, 2006, 28(9):1611-1613.

[9]ZHANG Dong-po, LIU Xing-zhao. A New Range Suppression Technique for Randomly Intermittent Spectra HF Radar Signal[J]. Journal of Shanghai Jiaotong University (Science), 2005, 10(2):112-116.

[10]朱凯, 王正林. 精通MATLAB神经网络[M]. 北京:电子工业出版社, 2010.

ZHU Kai, WANG Zheng-lin. Proficient in MATLAB Neural Network [M]. Beijing: Publishing House of Electronics Industry, 2010.

[11]张长胜. 多目标人工蜂群算法及遗传算法的研究与应用[M]. 沈阳:东北大学出版社, 2013.

ZHANG Chang-sheng. Research and Application of Multi-Objective Artificial Bees Colony Algorithm and Genetic Algorithm [M]. Shenyang: Press of Northeastern University, 2013.

[12]赵亮, 黄双华, 刘峰. 基于RBF神经网络的二相码旁瓣抑制[J]. 舰船电子对抗, 2010, 33(3):84-86.

ZHAO Liang, HUANG Shuang-hua, LIU feng. Binary-Coded Side-Lobe Suppression Based on RBF Neural Network [J]. Shipboard Electronic Countermeasure, 2010, 33(3):84-86.

LFM Signal Pulse Compression Based on GA-BP Network

YANG Ning-guo, REN Xin-tao

(PLA,No. 63863 Troop,Jilin Baicheng,137001 China)

Abstract:The application of error back propagation (BP) neural network to pulse compression of LFM (linear frequency modulation) is analyzed to improve the performance of pulse compression output of LFM. Genetic algorithm (GA) is utilized to conduct training study on the connection weight of BP neural network and such algorithm may overcome the defect that BP network easily falls into local optimum. The simulation result demonstrates GA-BP network features a faster rate of convergence and better numerical stability, and on the condition that the SNRL is less than 1 dB, the output main-to-side-lobe ratio of about 60 dB may be obtained.

Key words:linear frequency modulation(LFM); pulse compression; genetic algorithm(GA); GA-BP network; main-to-side-lobe ratio

中图分类号：TN958；TP183

文献标志码：A

文章编号：1009-086X(2015)-01-0076-05

doi:10.3969/j.issn.1009-086x.2015.01.013

通信地址：137001吉林省白城市108信箱23分队E-mail：renxintao2012@163.com

作者简介：杨宁国(1975-)，男，河北怀安人。工程师，硕士，研究方向为武器系统试验与鉴定。

收稿日期：2013-11-21；
修回日期：2013-12-31