助推-滑翔飞行器总体多学科设计优化研究*

范文锋，许波，郝昀

(北京机电工程总体设计部，北京　100854)



助推-滑翔飞行器总体多学科设计优化研究*

范文锋，许波，郝昀

(北京机电工程总体设计部，北京100854)

摘要：以助推-滑翔飞行器为研究对象，开展多学科设计优化在其总体设计过程中的应用研究。首先对助推-滑翔飞行器进行多学科设计优化任务分析、多学科建模，并建立了助推-滑翔飞行器总体多学科设计优化模型；其次对助推-滑翔飞行器总体设计学科间耦合特点进行分析，在此基础上提出了基于最优灵敏度方法的两层系统集成优化策略；最后通过数值优化算例验证了方法的有效性。优化结果表明，该方法具有较好的收敛速度，且使满载起飞质量减少9%，为高性能飞行器总体设计提供新的设计思路。

关键词：助推-滑翔飞行器；总体设计；多学科设计优化；最优灵敏度方法

0引言

临近空间通常指距离海平面20～100 km高度的空间范围。近年来，随着临近空间的拓展利用逐渐受到重视，助推-滑翔飞行器(boost-glide vehicle, BGV)成为国内外热点研究对象。典型包括俄罗斯的伊斯坎德尔战术导弹系统、美国的陆军战术导弹系统，其方案特点是采用固体火箭发动机快速助推爬升至弹道最高点，随后在临近空间内机动飞行直至命中目标；其总体特点是采用半弹道式飞行方案，大幅提升突防生存能力及精确打击能力，被誉为具有较高效费比的武器系统。

对BGV而言，其飞行弹道特征发生较大变化，由传统的弹道式轨迹转变为临近空间内的机动飞行轨迹，因而与总体性能相关的各专业学科之间设计关系发生较大变化，学科之间的耦合关系及设计矛盾更加突出。针对此类高性能飞行器总体设计，传统的串行设计方法已不能较好挖掘总体性能设计潜力，需要引入新的设计理念及思想进一步提升其总体设计水平[1]。多学科设计优化(multidisciplinary design optimization, MDO)自20世纪80年代初提出以来，已广泛应用于以飞行器为代表的复杂系统设计[2-5]，它是一种基于系统科学的思想，通过充分探索和利用复杂系统中相互作用的协同机制来进行优化设计[6]。将MDO应用于高性能飞行器总体设计过程，可以进一步挖掘总体设计的潜力，被认为是飞行器总体设计领域一次巨大的技术飞跃。

本文以BGV为研究对象，开展MDO在其总体设计过程中的应用研究。系统研究MDO任务规划及需求分析、多学科建模、系统分解与协调以及系统集成与求解等方面问题，为高性能飞行器总体设计提供新的设计思路。

1总体多学科设计优化任务分析

1.1基准方案及总体设计特点

本文BGV研究以国外某型飞行器总体方案为基准[7]，采用无翼式气动布局方案，在尾部布置空气舵实现姿态控制，通过单级固体火箭发动机助推爬升至弹道最高点，随后在临近空间机动滑翔飞行。

与传统弹道式飞行方案相比，BGV采用了临近空间机动滑翔的半弹道式飞行方案，与总体性能相关的各专业学科关系发生较大变化，耦合关系更加突出，其总体设计特点体现在以下几个方面：

(1) BGV最大射程除受到推重比的影响外，还受到气动升阻特性和弹道设计2种重要因素的影响，因此总体设计应重视发动机、质量、气动外形和弹道之间的耦合关系。

(2) 全程气动力控制方案要求气动外形设计应兼顾大范围飞行包络条件下的稳定性和操纵性，同时为满足射程指标又需兼顾发动机、质量优化的协调匹配关系，因此总体设计还应重视发动机、质量、气动外形和稳定控制之间的耦合关系。

1.2多学科设计优化任务

由BGV总体设计特点可知其MDO过程涉及外形、气动、质量、发动机、弹道和稳定控制共6个专业学科，通过学科之间的反复协调计算确定基准方案的具体参数，并使用寻优算法得到最优总体方案[4]。

BGV总体MDO的任务是将以上设计过程采用恰当的数学模型进行描述，根据总体设计耦合特点确定系统分解与协调策略，通过适当的系统集成并选用优化算法进行求解，充分挖掘BGV总体设计的潜力[5]。

2BGV多学科分析模型

2.1外形学科

外形学科分析模型的任务是对BGV的外形进行参数化建模，精确描述BGV的几何特征，并基于气动学科分析结果对BGV典型配平状态的升力特性、阻力特性以及配平特性进行分析，进一步对BGV的机动性、稳定性以及操纵性进行分析确认。

2.2气动学科

气动学科分析模型的任务是根据外形参数以及选定的飞行状态包络计算气动力数据。为确保气动计算的精确度和效率，文中采用气动工程估算软件DATCOM计算得到初步的气动数据，并采用基于CFD(computational fluid dynamics)的高精度修正方法进行修正，其修正公式为

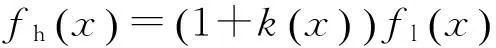
(1)

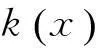
2.3发动机学科

发动机学科分析模型包括几何特性模型、质量特性模型以及性能分析模型。本文将发动机几何特性、质量特性模型分别划分至外形、质量学科，发动机学科重点突出性能分析模型。

固体火箭发动机性能分析模型中，推力系数为

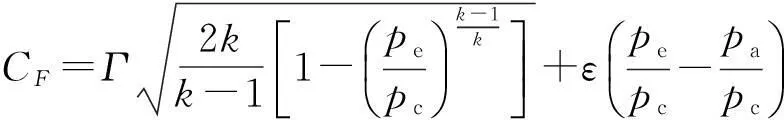
(2)

推力计算公式为

F=CFAtPc，

(3)

发动机比冲为

Is=c*CF,

(4)

2.4质量学科

质量分析模型包括导出型模型和展开型模型2种，其中展开型模型以飞行器各部件质量为基础，运用强度分析、几何尺寸和质量之间的关系建立模型，特点是过程繁琐但计算准确度高；导出型模型以设计参数和相对质量系数为基础，需要确定飞行器各基本参数间的关系式和相对质量系数，对工程经验依赖较多，特点是计算简单但准确度低。考虑到BGV多学科设计优化对质量学科的计算精度和效率需求，本文中质量学科分析模型综合应用导出型模型和展开型模型，其中发动机质量模型采用导出型模型，其他部分采用展开型模型。

BGV满载起飞质量计算公式为

m0=ms+mpl+mim+mf，

(5)

式中：m0为满载起飞质量；ms和mim分别为弹体结构质量和仪器设备质量，可根据统计经验给出；mpl为有效载荷质量，由战术技术要求给出；mf为固体火箭发动机质量。

固体火箭发动机质量计算公式为

mf=mp+mfs，

(6)

式中：mp为推进剂质量；mfs为发动机结构质量。

推进剂质量计算公式为

(7)

发动机结构质量计算公式为

mfs=mc+mn+mq，

(8)

式中：mn和mq分别为喷管和前、后裙的质量，可根据统计经验给出；mc为包含筒段、前后封头的壳体质量。

考虑前、后封头后的壳体质量计算公式为

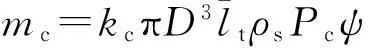
(9)

式中：kc为考虑前、后封头的质量系数；ρs为壳体材料密度；σ为壳体材料许用破坏应力；ψ为压强波动系数；φu为壳体材料安全系数。

2.5弹道学科

弹道分析是建立战术技术指标与总体参数之间关系的重要手段。弹道学科分析的任务是根据气动、发动机、质量等学科的分析结果，计算确定BGV的飞行特性，并为稳定控制学科分析提供相关数据支持。因此，弹道学科分析模型的准确性至关重要，本文中采用有控质点动力学模型描述BGV的飞行特性，其数学模型为[8]

(10)

根据BGV的弹道特点可将其飞行轨迹分为主动爬升段和再入滑翔段2部分。其中主动爬升段采用程序控制，通过程序角的控制实现飞行，依次为初始校正段、攻角转弯段、重力转弯段和瞄准段4部分[9]；再入滑翔段采用次优滑翔制导方法进行机动飞行[10]。

2.6稳定控制学科

稳定控制学科模型的任务是根据总体参数、弹道参数、气动参数以及各种偏差干扰，确定姿态角及角速度回路的控制参数，并得到系统能够达到的稳定裕度。通过稳定控制学科设计分析，可对弹体稳定性和操纵性给出定量评价，指导总体设计寻优过程。

3BGV总体MDO问题定义

3.1目标函数

根据BGV飞行任务特点及战术技术指标要求，本文中以给定射程指标条件下的满载起飞质量m0最小为优化目标。

3.2优化变量

BGV总体涉及外形、气动、质量、发动机、弹道及稳定控制共6个专业学科。根据各学科分析模型特点及数据流传递规律，可将外形、发动机及弹道3个学科的设计变量作为BGV总体多学科优化变量。

3.3约束条件

BGV总体MDO考虑的约束条件如下：

(1) 外形学科

(2) 发动机学科

喷管出口直径与发动机外径比值约束De/D≤0.7；

发动机质量比约束ηm>0.9；

(3) 弹道学科

驻点热流密度qws≤2 000 kW/m2；

终端速度约束vf≥400.0 m/s；

终端弹道倾角约束Θf≤-70°。

4总体设计的系统分解与协调策略

4.1BGV总体耦合特点分析

BGV总体涉及的6个专业学科之间的设计结构矩阵(design structure matrix, DSM)如图1所示。

图中矩形框代表不同的专业学科，黑色实心圆点表示数据流传递关系，矩阵左上三角部分表示学科之间的数据正馈，右下三角部分表示学科之间的数据反馈。

图1　BGV总体多学科设计结构矩阵Fig.1　DSM for BGV’s overall MDO

由图1分析BGV总体设计结构矩阵及数据传递关系，可知学科间存在以下耦合特点：

(1) 弹道学科是联系射程指标与总体设计参数之间的关键，直接确定外形、发动机与质量学科的设计指标；

(2) 弹道学科与其他5个学科两两之间均存在完整的数据正馈与反馈，因此弹道学科具有底层支撑作用；

(3) 气动、发动机与质量3个学科之间不存在反馈回路，各学科在优化过程中所需数据由其他学科提供，因此学科分析结果由其他学科设计变量确定。

4.2系统分解及协调策略

根据BGV总体设计的耦合关系特点，借鉴现有MDO优化策略[11]，提出适用于BGV总体MDO的两层系统集成优化(bi-level system integrated optimization, BLSIO) 策略，其原理结构如图2所示。

图2　基于最优灵敏度的两层系统集成优化策略Fig.2　Bi-level system integrated optimization　　　strategy based on OSM

BLSIO策略是从弹道学科在总体设计过程中的特殊作用以及BGV总体相关学科之间的耦合调用关系出发，其基本思想是将弹道学科作为内层进行优化，其他5个学科作为外层进行优化，内层对外层的影响通过最优灵敏度方法[12](optimal sensitivity method, OSM)进行处理。系统优化过程描述如下：

(1) 给定(外层)弹道学科和(内层)外形学科、发动机学科的优化设计变量初始值。

(2) 采用定点迭代法(fixed point iteration, FPI)进行外层多学科分析(multi-disciplinary analysis, MDA)。首先进行外形、气动、发动机和质量4个学科的分析计算，得到BGV的几何特性、气动特性、发动机推力特性和质量特性数据，为内层弹道优化提供所需数据；其次进行内层弹道优化计算，得到BGV飞行特性数据；最后基于弹道学科输出的动力系数等进行闭环稳定控制分析，得到BGV闭环稳定裕度。

(3) 进行系统灵敏度计算，将外层目标函数、约束函数值以及相关灵敏度信息传递给外层优化器进行寻优。

(4) 判断是否满足系统收敛准则，若满足则停止优化迭代，并输出系统优化变量和目标函数值，否则更新外层优化变量，返回步骤(2)进行下一轮优化迭代。

5优化算例

本文中优化算例以国外某型飞行器单级总体方案为基准，以某一给定射程为性能指标，采用第3节中的MDO模型，使用BLSIO策略进行系统分解与集成求解，其中内层和外层优化器均基于序列二次规划方法(sequential quadratic programming, SQP)实现。

优化过程经过23次系统迭代满足收敛准则而停止，优化结果如表1所示，归一化满载起飞质量收敛过程如图3所示。优化结果表明归一化满载质量结果为0.91，即通过系统优化使满载起飞质量减少9%。

此外，通过优化迭代收敛得到如下几点认识：

(3) 外形基本确定后，发动机的燃烧室压强Pc越高，则推力越大，对主动段控制特性有利，但同时降低了发动机质量比，不利于能量的利用，因此燃烧室压强的确定也需要仔细权衡处理。

(4) 增加喷管扩张比ε有利于提高比冲及总冲，对增加射程有利；但随着ε的增加，发动机质量比下降，又导致射程损失，同时使质心后移，对全程稳定控制不利，因此ε的确定需要考虑射程要求和稳定控制对质心位置的要求。

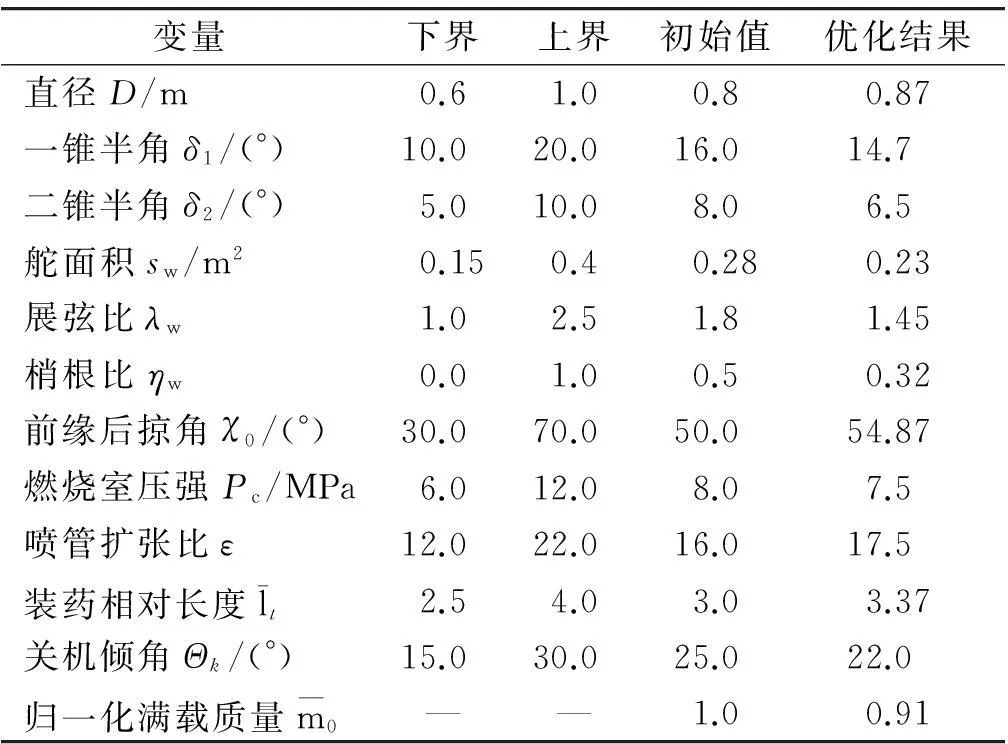
表1　BGV多学科优化结果

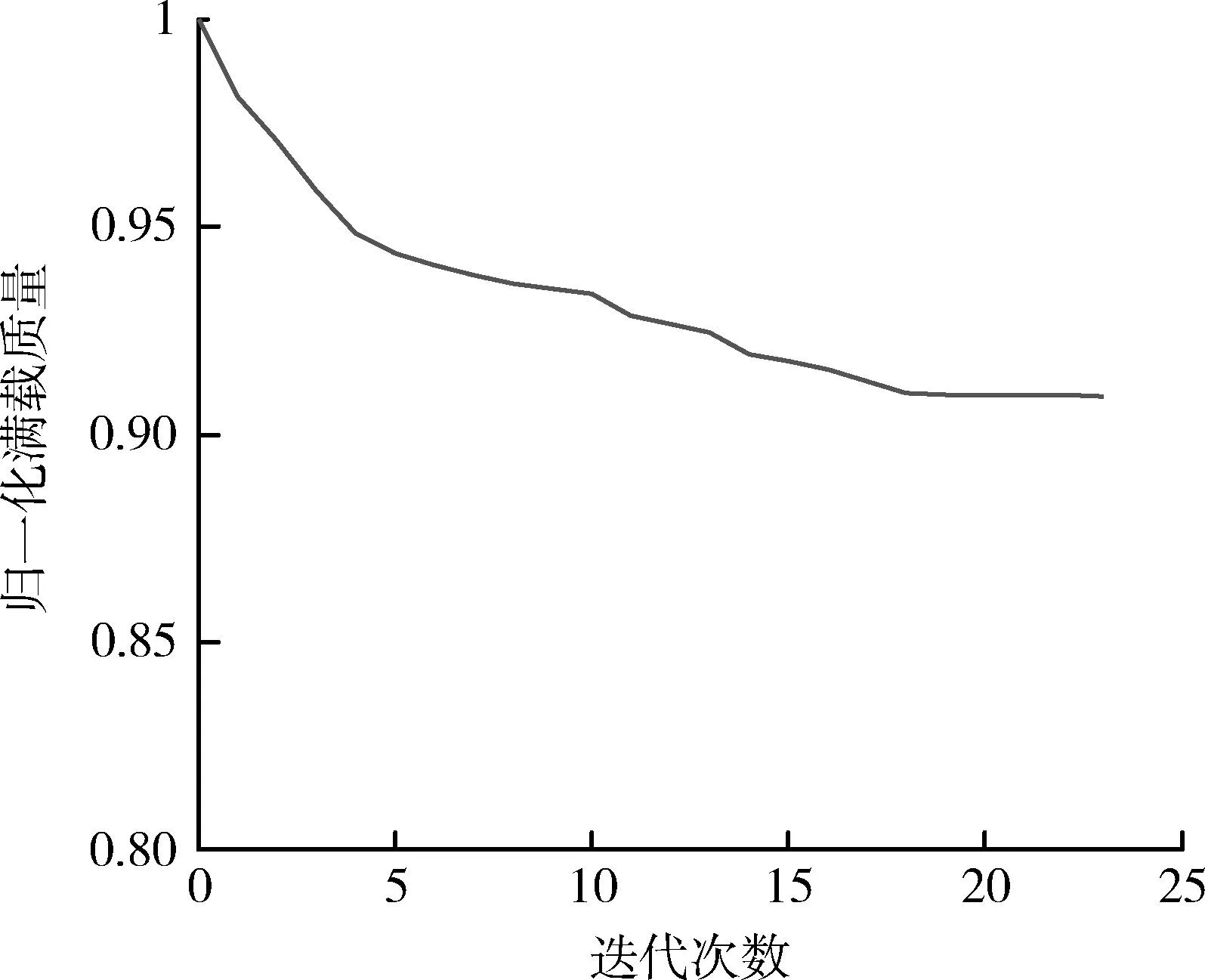
图3　归一化满载质量收敛过程Fig.3　Course for non-dimensional launch weight

6结论

本文以BGV为研究对象，开展MDO在其总体设计中的应用研究，系统研究了MDO任务规划及需求分析、多学科建模、系统分解与协调以及系统集成与求解等方面问题，并通过数值算例进行了验证，得出以下结论：

(1) BGV半弹道式飞行方案决定了其总体设计应主要关注外形、气动、质量、发动机、弹道及稳定控制6个学科，各学科之间耦合关系复杂；总体设计时应重点关注发动机、气动外形、质量、弹道之间的耦合关系，此外还应关注发动机、气动外形、质量及稳定控制之间的耦合关系。

(2) 根据BGV总体设计特点以及学科间逻辑耦合特点，提出基于最优灵敏度方法的两层系统集成优化策略，较好的解决了学科之间的耦合关系，为获取系统最优解提供了较好的解决思路。

(3) BGV总体设计采用MDO方法可充分利用学科间的协同作用，进一步挖掘总体性能设计潜能，适用于高性能飞行器总体设计过程。

参考文献：

[1]常泊浚. 飞行力学设计的新思路[J]. 中国科学E辑:技术科学, 2009, 39(3): 575-578.

CHANG Bo-jun. New Reflections on Flight Mechanics Design[J]. Science China Technology Science, 2009, 39(3): 575-578.

[2]王健, 何麟书. 基于增强协同优化的助推-滑翔导弹概念研究[J]. 宇航学报, 2009, 30(6): 2436-2441.

WANG Jian, HE Lin-shu. Boost-Glide Missile Conceptual Study Based on Enhanced Collaborative Optimization[J]. Journal of Astronautics, 2009, 30(6): 2436-2441.

[3]马英, 何麟书, 段勇. 基于多学科设计优化弹道导弹概念设计研究[J]. 计算机集成制造系统, 2007, 13(12): 2289-2293.

MA Ying, HE Lin-shu, DUAN Yong. Ballistic Missile Conceptual Design Based on Multidisciplinary Design Optimization[J]. Computer Integrated Manufacturing Systems, 2007, 13(12): 2289-2293.

[4]龚春林, 谷良贤, 粟华. 亚轨道重复使用运载器总体多学科优化方法[J]. 固体火箭技术, 2012, 35(1): 5-10,16.

GONG Chun-lin, GU Liang-xian, SU Hua. Multidisciplinary Design Optimization Method for Suborbital Reusable Launch Vehicle[J]. Journal of Solid Rocket Technology, 2012, 35(1): 5-10,16.

[5]张菲, 任全彬, 杨军, 等. 基于多学科设计优化的空地导弹概念设计[J]. 固体火箭技术, 2013, 36(2): 149-154.

ZHANG Fei, REN Quan-bin, YANG Jun, et al. Air-to-Ground Missile Conceptual Design Based on Multidisciplinary Design Optimization[J]. Journal of Solid Rocket Technology, 2013, 36(2): 149-154.

[6]蒋鲁佳, 辛万青, 赵雯, 等. 多学科设计优化在飞行器总体设计中的应用[J]. 弹箭与制导学报, 2012, 32(3): 39-43.

JIANG Lu-jia, XIN Wan-qing, ZHAO Wen, et al. The Application of Multidisciplinary Design Optimization in Aircraft System Design[J]. J. of Projectiles, Rockets, Missiles and Guidance, 2012, 32(3): 39-43.

[7]顾正明, 王益群. 国外近程战术地地导弹和反战术弹道导弹的发展概况[J]. 系统工程与电子技术, 1990, (1): 66-69.

GU Zheng-ming, WANG Yi-qun. Recent Development and Trend of TBM and ATBM Abroad[J]. Systems Engineering and Electronics, 1990, (1): 66-69.

[8]赵汉元. 飞行器再入动力学与制导[M]. 长沙:国防科技大学出版社, 1997.

ZHAO Han-yuan. Reentry Dynamics and Guidance for Flight Vehicles[M]. Changsha: National University of Defense Technology Press, 1997.

[9]贾沛然, 陈克俊, 何力. 远程火箭弹道学[M]. 长沙: 国防科技大学出版社, 1993.

JIA Pei-ran, CHEN Ke-jun, HE Li. Long Range Rocket Ballistics[M]. Changsha: National University of Defense Technology Press, 1993.

[10]胡锡精, 严卫钢, 黄雪梅. 基于奇异摄动与反馈线性化的滑翔制导律[J]. 航天控制, 2011, 29(2): 10-14, 22.

HU Xi-jing, YAN Wei-gang, HUANG Xue-mei. Gliding Guidance Law Based on Singular Perturbation and Feedback Linearization[J]. Aerospace Control, 2011, 29(2): 10-14, 22.

[11]王振国, 陈小前, 罗文彩, 等. 飞行器多学科设计优化理论与应用研究[M]. 北京: 国防工业出版社, 2006.

WANG Zhen-guo, CHEN Xiao-qian, LUO Wen-cai, et al. Research on the Theory and Application of Multidisciplinary Design Optimization of Flight Vehicles[M]. Beijing: National Defense Industry Press, 2006.

[12]颜力, 陈小前, 王振国. 飞行器多学科设计优化中的灵敏度分析方法研究[J]. 航空计算技术, 2005, 35(1): 1-6.

YAN Li, CHEN Xiao-qian, WANG Zhen-guo. The Study of Sensitivity Analysis in the Multidisciplinary Design Optimization of flying Vehicles[J]. Aeronautical Computer Technique, 2005, 35(1): 1-6.

Multidisciplinary Design Optimization for Boost-Glide Vehicle Overall Design

FAN Wen-feng，XU Bo，HAO Yun

(Beijing System Design Institute of Mechanical-Electrical Engineering, Beijing 100854,China)

Abstract:The application of multidisciplinary design optimization (MDO) for boost-glide Vehicle (BGV)’s overall design is addressed. First, mission defining and multidisciplinary modeling are investigated, and the MDO problems for BGV’s overall design are presented. Second, the system coupling characteristics for BGV are analyzed, and then a Bi-level system integrated optimization (BLSIO) strategy based on the optimal sensitivity method (OSM) is proposed for BGV’s MDO. Lastly, a numerical example is tested to explain the method’s effectiveness. The results indicate that the BLSIO has extreme convergence, and the launch weight for BGV deceases by 9%, the proposed method gives new clues for high performance flight vehicles.

Key words:boost-glide vehicle(BGV); overall design; multidisciplinary design optimization(MDO); optimal sensitivity method

中图分类号：V421.1;TJ01

文献标志码：A

文章编号：1009-086X(2015)-01-0046-06

doi:10.3969/j.issn.1009-086x.2015.01.008

通信地址：100854北京142信箱206分箱E-mail：jaly1314@sina.com

作者简介：范文锋(1981-)，男，陕西渭南人。博士生，主要研究方向为飞行器总体设计。

基金项目：有

收稿日期：2014-02-13；
修回日期：2014-04-09