电动舵机动力学与旋转导弹转速关系研究*
2015-03-09许超,石德平,高庆丰
电动舵机动力学与旋转导弹转速关系研究*
许超1,石德平2,高庆丰1
(1.北京电子工程总体研究所,北京100854; 2.中国航天科工集团 第二研究院,北京100854)
摘要:利用准弹体坐标系下舵机环节传递函数,推导了由舵机延迟而产生方位误差的表达式。将此方位误差等效为控制回路耦合,通过分析横向偏差和视线角速率等性能指标,得到旋转弹转速和电动舵机无阻尼自振频率的约束关系,为旋转弹转速设计和电动舵机设计提供参考,具有一定的理论和工程价值。
关键词:旋转弹;转速;电动舵机;方位误差;制导回路
0引言

造成方位误差和交叉耦合的主要因素如下:①由于舵机延迟造成的舵机环节交连干扰;②由于惯性力矩和马格努斯力矩引起的弹体环节交连干扰[1]。电动舵机采用正弦控制信号,由于舵机延迟必然引起控制信号偏差,从而产生交叉耦合。随着导弹转速的增大,由此产生的控制误差将随之增大,这对导弹实现正确导引将产生极为不利的影响[2]。因此在旋转弹转速设计时,必须考虑舵机动力学的限制。
本文将通过由舵机延迟而产生方位误差角的大小,研究电动舵机动力学与旋转弹转速的定量关系。为此,首先研究由于舵机延迟所引起的方位误差的定量关系式,然后将方位误差视为控制回路交连,代入旋转弹的制导回路,通过对制导回路各项性能指标的仿真分析,最终给出转速设计上界与舵机动力学的制约关系。
1电动舵机引起方位误差
1.1制导回路模型
在不采用自动驾驶仪时,单通道旋转弹在准弹体坐标系上的制导回路结构图,可等效为如图1所示[3]。
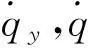
1.2舵机无阻尼自振频率与方位误差定量关系
设舵系统模型为二阶振荡环节,不失一般性,取舵系统动力学环节的增益为1,其数学模型为[5]

(1)
式中:ωs为舵机的无阻尼自振频率;μs为舵系统的阻尼比。
ωs表征了舵机延迟大小,即舵机无阻尼自振频率越大,舵机响应越快,舵机延迟越小。
由文献[6]可得,单通道旋转弹舵系统在准弹体系下的传递函数矩阵可表示为
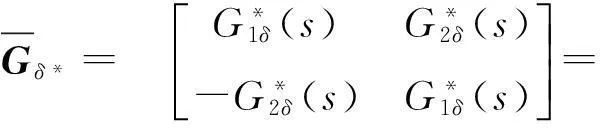

(2)

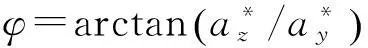
则舵机延迟引起的方位误差稳态值为[8]
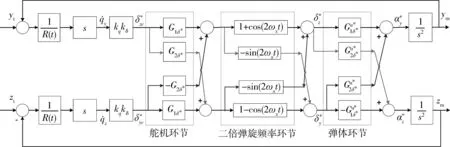
图1 单通道旋转弹制导回路结构图Fig.1 Guidance loop block diagram of rolling missiles with single channel control
图2 方位误差Fig.2 Direction error
(3)
假设旋转弹的设计转速为10 r/s,而在整个飞行过程中,转速的变化范围在8~14 r/s。设舵机阻尼比ξs为0.5,则在不同转速下,方位误差与舵机无阻尼自振频率的关系如图3所示。
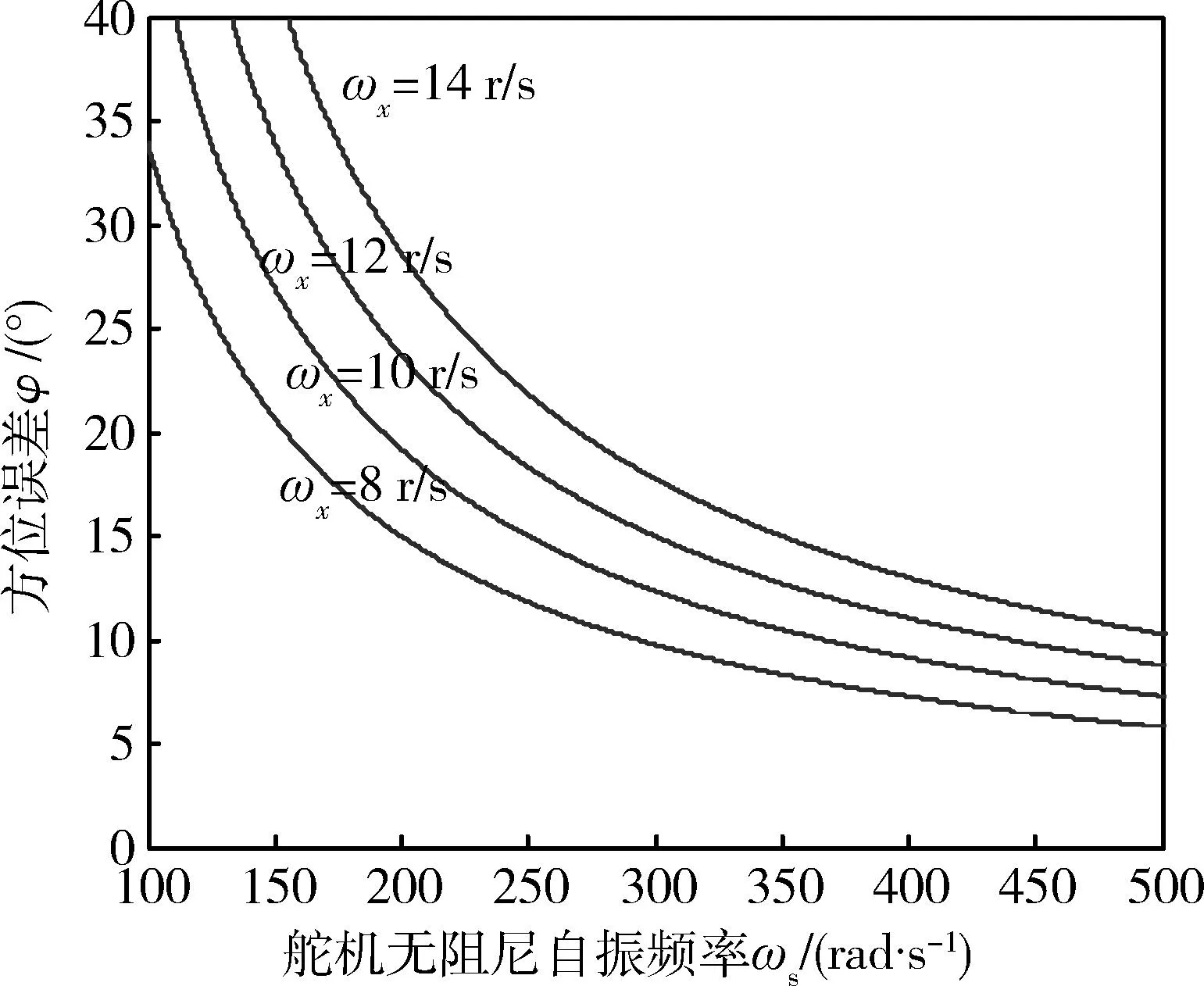
图3 方位误差与舵机无阻尼自振频率关系曲线Fig.3 Relationship between direction error and actuator undamped natural frequency
2方位误差对导引性能的影响
2.1理想弹体制导回路模型
为分析舵机延迟对于导引性能的影响,首先忽略弹体环节和二倍弹旋频率干扰引起的交连耦合,同时将弹体设为理想弹体,令

(4)
称N为有效导航比,当弹体为理想弹体时,N为常数[9]。而舵机环节的交连耦合可用方位误差代替,此时制导回路结构图可简化如图4所示。

图4 理想弹体制导回路结构图Fig.4 Guidance loop block diagram in the ideal missile system
2.2制导回路性能仿真
设典型的低空导弹拦截关系为:目标在空中悬停,高度为100 m,在导弹发射时刻导弹与目标在同一与大地垂直的平面内,大地投影距离为1 500 m,导弹飞行速度为500 m/s。为分析方便,设导弹初速度方向为水平方向,并指向目标在大地上的投影点。这相当于yt为阶跃输入,zt=0。令
N/R(t)=K,
(5)
同时将R(t)固化,则由结构图4可得
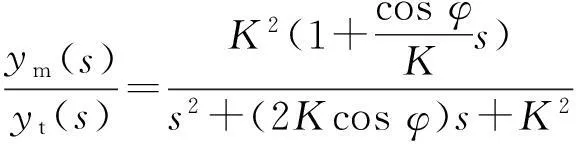
(6)
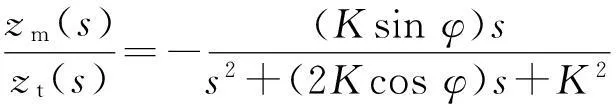
(7)
可见φ直接影响系统品质及稳定性。φ≥90°时,系统将失稳。进一步,当yt为阶跃输入时,可解得
ym=100[1-e-Kcosφ·tcos(Ksinφ·t)],
(8)
zm=-100e-Ksinφ·tsin(Ksinφ·t).
(9)
可以看出,导弹飞行弹迹是螺旋的,原来在垂直平面上的导引出现横向偏差,近似的有收敛半径100e-Kcosφ·t,角速度Ksinφ[10]。
横向偏差的大小直接反映了导弹弹道的飞行精度[11]。由图5中可以看出,当方位误差角φ=10°时,偏航误差zm不超过6 m;而且随着方位误差角的增大,偏航误差不断增大,而且增大速度快于线性增长速度。当方位误差达到φ=45°时,此时的偏航误差将超过25 m。
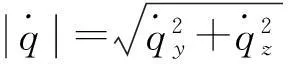
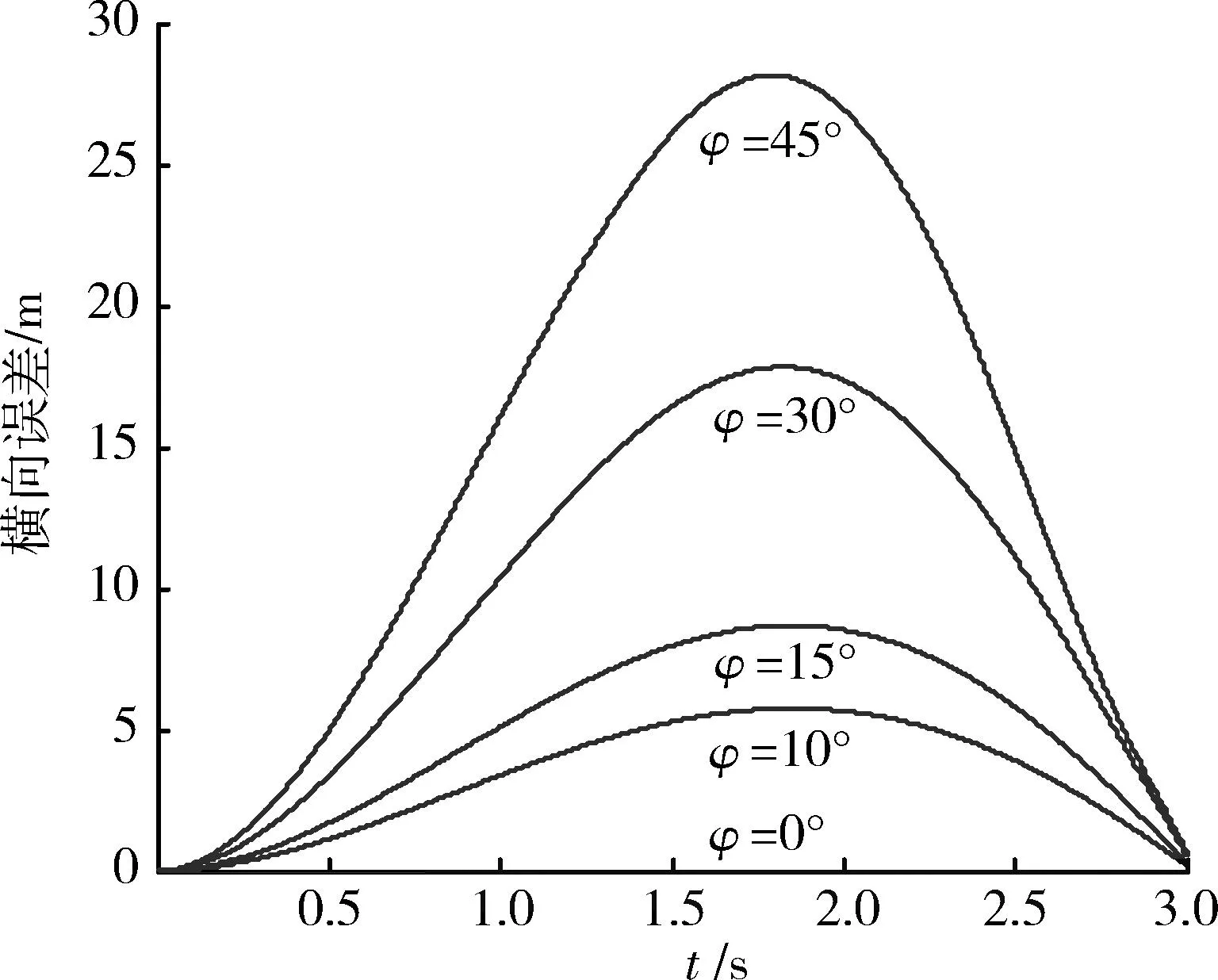
图5 横向误差变化曲线Fig.5 Lateral position curves with different direction errors
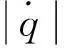
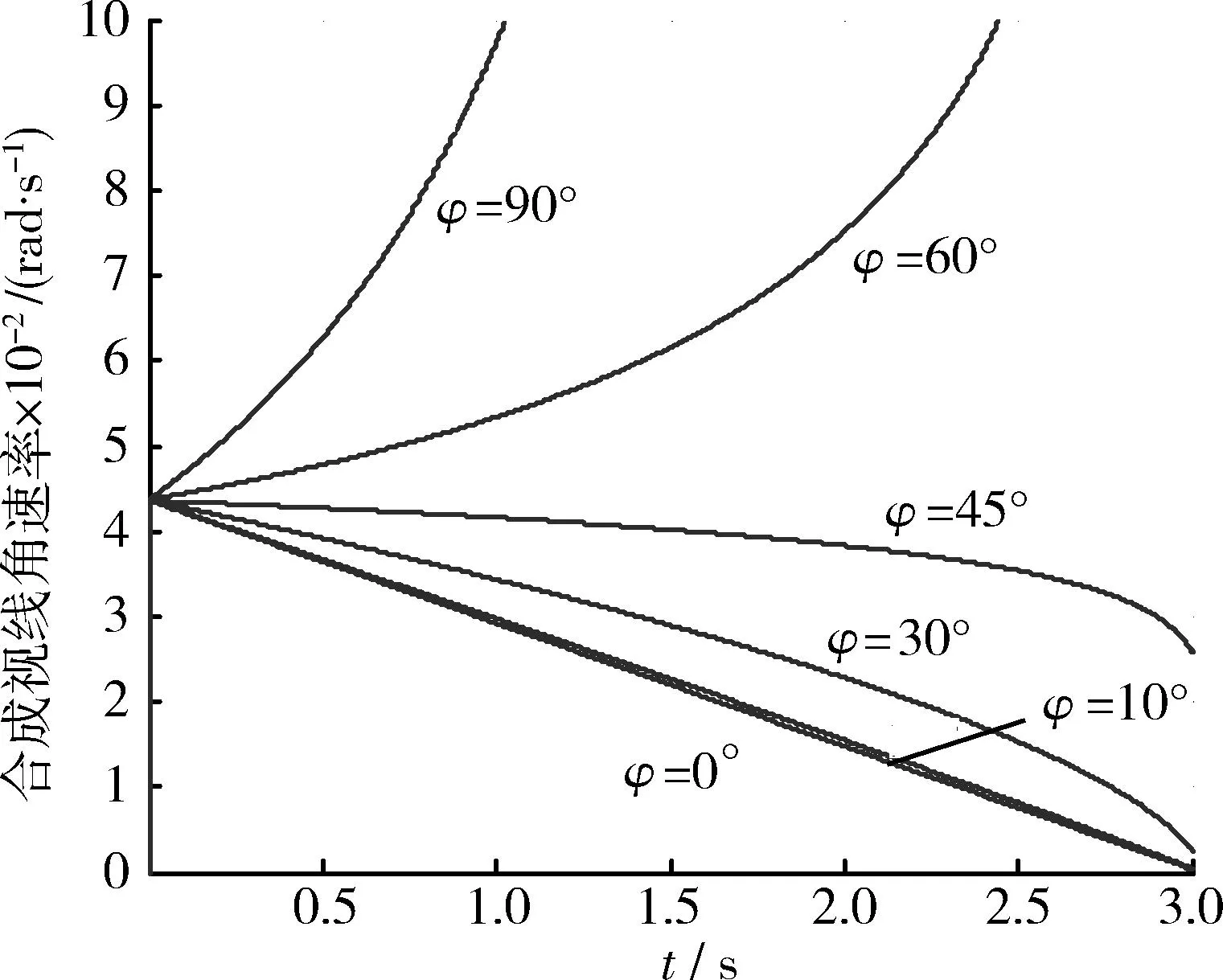
图6 合成视线角速率变化曲线Fig.6 Synthetized LOS rate with different direction errors
分别观察y方向和z方向的视线角速率,还能得出如下结论:随着方位误差φ的增大,视线角速度出现较大的振荡,视线角速度发散时间提前,导引回路提前失稳。为响应视线角速度的变化,势必要求更大的过载。φ<10° 时,系统变化不明显,仍可实现正确导引;φ>15°后,视线角速度出现振荡,此时弹迹是螺旋的;并且随φ角的增大,振荡加剧且振荡时间提前。
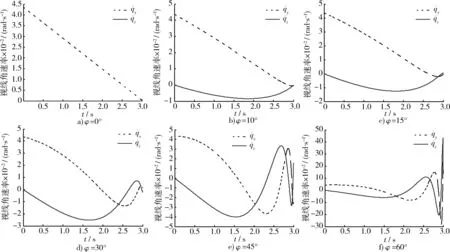
图7 视线角速率变化曲线Fig.7 LOS rate curves with different direction errors
3舵机延迟与旋转弹转速关系
在不同方位误差角下,舵机无阻尼自振频率与旋转弹转速关系如图8所示。

图8 舵机无阻尼自振频率与旋转弹转速关系曲线Fig.8 Relationship between actuator undamped natural frequency and rotation rate
由图8可知,当导弹转速上限ωx=14 r/s时[12],舵机无阻尼自振频率上限与方位误差的关系如表1所示。

表1 转速上限与方位误差关系
同时,结合上节分析可知,当方位误差在10°内,方位误差对系统导引性能造成的影响尚不明显。因此以方位误差≤10° 为设计指标,得到的旋转弹转速上界为14 r/s时,舵机无阻尼自振频率设计要求为
max (ωs)≥514.0 rad/s.
(10)
通过以上分析可以得出:当旋转弹设计转速为10 r/s,转速变化范围在8~14 r/s,为实现正确导引,二阶舵机模型的无阻尼自振频率ωs的设计上界不得低于514.0 rad/s。
4结束语
单通道旋转导弹采用电动舵机作为执行机构时,由于舵机延迟将不可避免的产生控制耦合。本文首先建立了电动舵机动力学与制导回路方位误差的定量关系,然后研究了方位误差对制导回路性能的影响,最后将方位误差作为限制指标,给出了旋转弹转速上限与舵机无阻尼自振频率的约束关系。本文的研究可以为旋转弹转速设计和电动舵机设计提供参考,具有一定的理论和工程价值。
参考文献:
[1]王宗义. 方位误差对自旋导弹导引性能的影响[J].弹箭与制导学报,2003,23(6):5-8.
WANG Zong-yi. Effect of Direction Error on Guidance Performance of Spinning Missiles[J].Journal of Projectiles,Rockets,Missiles and Guidance,2003,23(6):5-8.
[2]于剑桥,文仲辉,梅跃松. 战术导弹总体设计[M]. 北京:北京理工大学出版社, 2010:188-197.
YU Jian-qiao, WEN Zhong-hui, MEI Yue-song. The General Design of Tactical Missiles[M]. Beijing:Beijing Institute of Technology Press,2010:188-197.
[3]钱杏芳,林瑞雄,赵亚男. 导弹飞行力学[M]. 北京:北京理工大学出版社, 2000:64-74.
QIAN Xing-fang, LIN Rui-xiong, ZHAO Ya-nan. Missile Flight Dynamics[M].Beijing: Beijing Institute of Technology Press,2000:64-74.
[4]陈罗婧,刘莉,于剑桥.双通道旋转导弹自动驾驶仪回路的数学变换及其耦合性分析[J].北京理工大学学报,2007,27(10):848-850.
CHEN Luo-jing, LIU Li, YU Jian-qiao. Transform and Coupling Analysis of Double Channel Control Rolling Missile Autopilot Loop[J]. Transactions of Beijing Institute of Technology, 2007,27(10):848-850.
[5]Paul Zarchan. Tactical and Strategic Missile Guidance[M].6th Edition. American Institute of Aeronautics and Astronautics, Inc.2012:537-538.
[6]高庆丰,陈罗婧. 单通道自旋导弹自动驾驶仪回路的变换及其简化[J]. 现代防御技术,2010,12(6):61-65.
GAO Qing-feng, CHEN Luo-jing. Autopilot Design of Single Channel Rolling Missile[J]. Modern Defence Technology,2010,12(6):61-65.
[7]李衡. 旋转弹总体问题研究[D]. 北京:中国航天第二研究院,2011:40-41.
LI Heng. The General Technology Research on Rolling Missile[D]. Beijing:The Second Academy of China Aerospace. Dissertation for the Master Degree in Engineering,2011:40-41.
[8]胡寿松. 自动控制原理[M]. 北京:科学出版社,2006:107-109.
HU Shou-song. The Theory of Automatic Control[M].Beijing:Science Press,2006:107-109.
[9]GARNELL P. Guided Weapon Control Systems[M].2nd ed. QI Zai-kang,XIA Qun-li,Translated. Bejing:Beijing Institute of Technology, 2004:303-306.
[10]湛必胜,秦志强,王明海.螺旋载入弹道特性分析[J].弹道学报,2006,18(3):18-20.
ZHAN Bi-sheng, QIN Zhi-jiang,WANG Ming-hai. Analysis of Characteristics of Spiral Reentry Trajectory[J]. Journal of Ballistics,2006,18(3):18-20.
[11]冯融冰,郑世勇,程延杰. 基于Simulink的防空导弹单发杀伤概率仿真研究[J].舰船电子工程,2011,31(11):82-84.
FENG Rong-bing, ZHENG Shi-yong,CHENG Yan-jie. Research on Kill Probability of Single Air Defense Missile Based on Simulink[J]. Ship Electronic Engineering,2011,31(11):82-84.
[12]李朝福. 提高电动舵机动态特性的方法研究[J]. 战术导弹控制技术, 2008,30(2):39-40.
LI Chao-fu. Research on Improve the Dynamic Characteristic of Electric Control Actuator[J]. Control Technology of Tacticle Missile,2008,30(2):39-40.
Research on the Relationship Between Electromechanical Actuator Dynamics and Rotation Rate of Rolling Missile
XU Chao1, SHI De-ping2, GAO Qing-feng1
(1.Beijing Inst. of Electronic System Engineering, Beijing 100854, China;2. The Second Research Academy of CASIC, Beijing 100854, China)
Abstract:The formula about the direction error caused by electromechanical actuator delay is established, using the actuator loop transfer function under quasi-body coordinate system. Taking the direction error as the coupling of motion on guidance loop, the constrained relationship between rotation rate and actuator undamped natural frequency is given by analyzing the values of lateral position error and LOS rate. It will be theoretically and practically significant in both the rotation rate design and actuator design of a rolling missile.
Key words:rolling missile; rotation rate; electromechanical actuator; direction error; guidance loop
中图分类号:TJ760.1; TP391.9
文献标志码:A
文章编号:1009-086X(2015)-02-0029-05
doi:10.3969/j.issn.1009-086x.2015.02.006
通信地址:100854北京142信箱30分箱E-mail:hitsaxuchao@gmail.com
作者简介:许超(1989-),男,云南陆良人。硕士生,主要研究方向为飞行器总体设计。
基金项目:有
* 收稿日期:2014-01-21;
修回日期:2014-03-13
