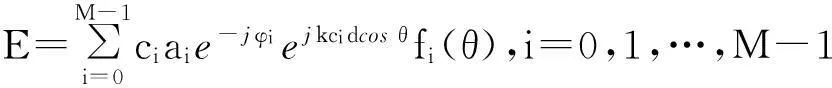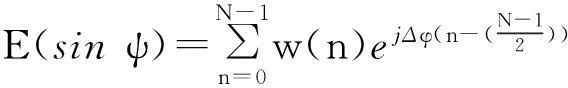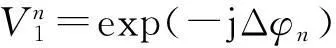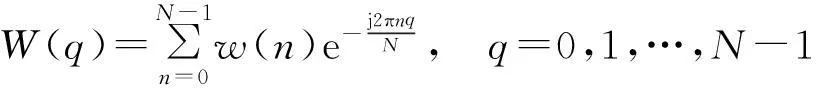基于失效阵元位置优化的天线方向图重构*1
2015-03-09周志增,丁桂强,康鹏等
基于失效阵元位置优化的天线方向图重构*1
周志增,丁桂强,康鹏,高风华
(中国洛阳电子装备试验中心,河南 孟州454750 )
摘要:阵元失效会破坏雷达阵列响应,为降低影响,利用遗传算法以失效位置为优化对象,以副瓣和波束宽度为约束标准建立优化模型,同时结合FFT快速算法以提高运算效率。仿真结果表明,遗传算法显著提高了阵列方向图的主副瓣比,能很好地解决大型阵面的阵元位置寻优问题。
关键词:阵元失效; 副瓣; 波束宽度; 遗传算法
0引言
相控阵雷达天线能够灵活、无惯性地将波束扫描至预期的方向上,在空间进行功率合成,在指定的区域中进行搜索、识别和跟踪多目标,对目标的捕获率大且工作稳定可靠,因此在雷达对抗和各种电子战中的应用越来越广泛。相控阵阵面由于由多个阵列单元组成,具有很高的可靠性。但是,阵列单元失效也是实际应用中很可能出现的问题,器件老化、受外界物理损坏等因素都可能导致天线阵列单元失效,甚至天线子阵失效。阵列单元失效会引起阵列响应发生变化,从而造成雷达副瓣电平和天线增益的恶化,失效单元超过一定数量会严重影响到雷达的探测性能。因此,在一定数量阵列单元失效情况下而短时间内无法更换受损单元时,研究如何改善阵列性能关系到实装的参试质量和参训效果[1-2]。
一般来说,改善阵列性能有2种方法:一是对正常工作阵元的激励权重重新进行优化,以重新构建天线方向图。这种方法的优点是不用对雷达阵面进行维修,但带来的是雷达后续计算和系统设计的复杂性,操作性不强。另一种方法是对正常阵元的位置进行调整,以达到补偿失效单元输出的作用。此方法实现起来较为容易,且具有较强的灵活性。本文正是基于这种考虑,探讨一种如何利用遗传算法优化雷达阵面性能的方法。
1天线模型及FFT算法
1.1天线模型
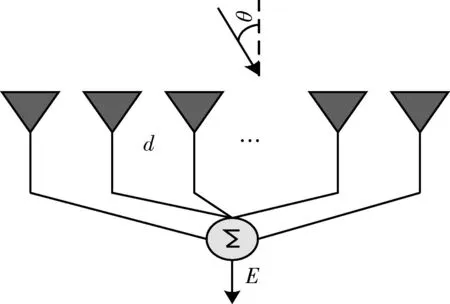
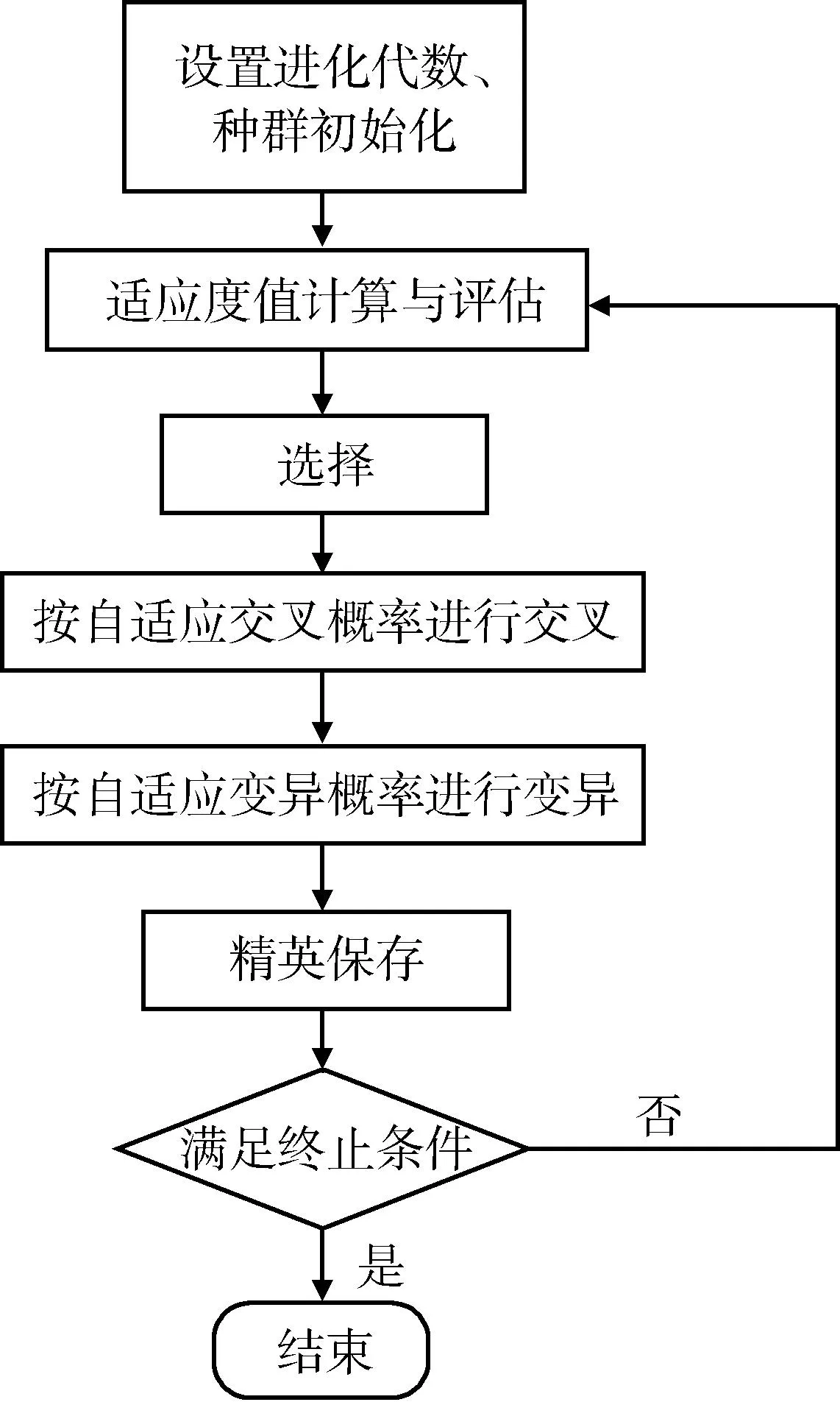
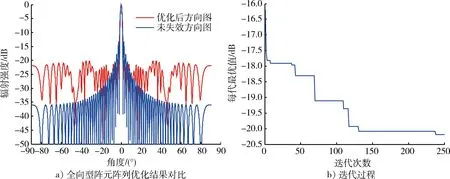
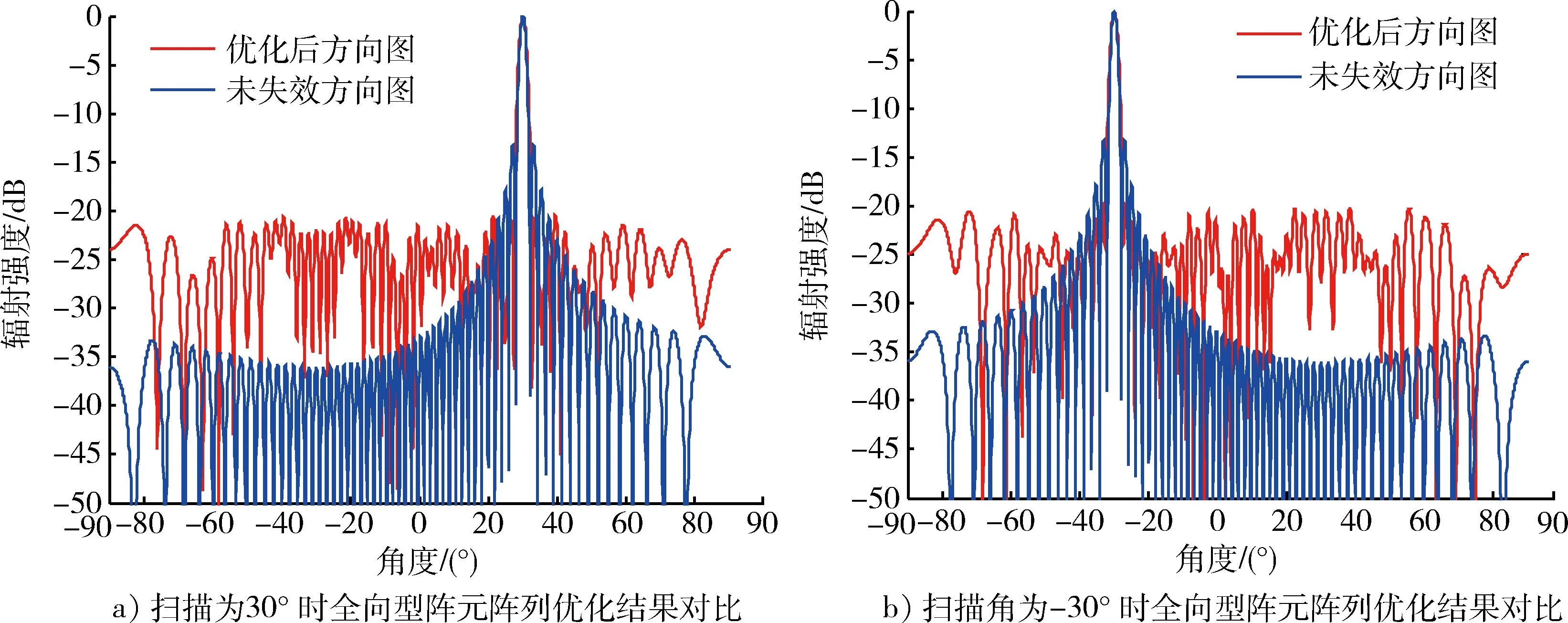
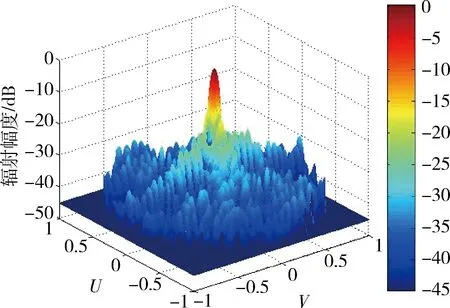
如图1所示,由M个单元组成的线阵,单元间距为d,阵元的激励幅度为ai,相位为φi,单元是否激励用ci表示,假设只选择其中m (1) 式中:f(θ)为单个阵元的辐射特性,可设为全向型和余弦函数型;θ为平面波与阵面法线的夹角。由于波束宽度与天线的孔径成反比,为了保证波束的原有宽度变化不大,假设线阵两端的阵元为正常工作状态,以满足孔径要求。主要是合理调整中间的单元的位置,以抑制波束副瓣。 图1 线阵模型Fig.1 Linear array model 可见,阵列阵元的幅度、相位和位置关系都会影响到天线的输出,本文假设正常阵元电流幅度都为1,相位不变,主要以失效阵元的位置为优化参量。 对于采用矩形阵面的阵列结构,采用二维可分离对称激励,阵列的阵因子可表示为 F(θ,φ)=∑∑Imncos[(2m-1)πdxsinθ+… +cosφ]cos[(2n-1)πdysinθsinφ], (2) 式中:Imn为第m行n列所对应阵元的电流幅度;dx,dy为阵元间距;θ,φ为阵轴线与射线间的夹角。 1.2FFT算法 算法在迭代过程中要结合适应度函数反复计算方向图函数的采样点来评估个体的优劣。适度降低计算时间就能够减少评估个体的时间,从而大大提高算法的运行速度。对于一个规则栅格的阵列天线,这可以通过离散傅里叶变换(discrete Fourier transform,DFT) 来计算,从而运用快速傅里叶变换来实现。 图1给出了单位间距为d、波长为λ的线性阵列。辐射器为D=d的天线阵元。令w(n)和φ(n)相应地表示锥削和相移序列[4]。在方向正弦sinψ的远场点上的归一化电场为 (3) 式中:在这种情况下,相位基准被取为阵列的物理中性,而且 (4) 展开式(3)并提出公共的相位因子exp[j(N-1)·Δφ/2],得到 E(sinφ)=ej(N-1)Δφ/2[w(0)e-j(N-1)Δφ+… +w(1)e-j(N-2)Δφ+…+w(N-1)]. (5) 利用加窗序列的对称性,可以写成 E(sinφ)=ejφ0[w(N-1)e-j(N-1)Δφ+… +w(N-2)e-j(N-2)Δφ+…+w(0)], (6) 式中:φ0=(N-1)Δφ/2。 由此,序列w(n)的离散傅里叶变化为 (7) 在(θ)域中,其计算时间正比于N2,而FFT计算时间正比于NlbN。计算的时候究竟快多少,还一定程度上取决于采样点数、FFT的细节。同样,这种方法也可以用于平面阵列优化的方向图计算中。 2遗传算法实现 遗传算法(genetic algorithms,GA)是一种基于生物自然选择和遗传机理的启发式优化算法,它将影响问题结果的参数变量编码成染色体,采用适值函数衡量各染色体的优劣程度,经过交叉和变异引导搜索向更高的结果(问题的最优解)迭代,适者生存,优胜劣汰。其关键是选择合理的编码方式,适值评估函数,以及交叉和变异概率的控制。遗传算法在阵列优化中已经取得了广泛的应用[5-7]。 遗传算法综合步骤如下: (1) 以失效单元位置优化参量,进而对参量进行编码,生产初始种群。 对于一个阵列天线,假总阵阵元数为63,失效阵元数为13,阵元间距为0.5λ(λ为波长),各天线阵元辐射特性都是相同的。采用遗传算法优化阵元位置,使阵列天线具有窄的主瓣宽度和低的副瓣。根据孔径要求,首尾2个阵元ci设为1,在61个可选位置中选出50处放置阵元,采用二进制对这些位置进行编码。 (2) 建立适应度评估模型,基于天线阵因子模型。适应度函数为abs(F(φ)),abs为对函数取绝对值。 最大相对旁瓣电平MSLL的计算公式为 MSLL=max {F(φ) },φ∈S, 式中:max 为求最大值函数;S为方向图的旁瓣区域。如果主瓣的零功率宽度为2θ0,则S={φ|0≤φ≤90°-θ0或90°+θ0≤φ≤180°},实际计算时需对S以一定间隔(如0.2°) 离散,MMLL为主瓣电平,MBW为波束宽度。 F(φ)=α|MMLL/MSLL|+β|1/MBW|, (8) 式中:α和β为权系数,和为1,其值可灵活调整以满足对副瓣和波束宽度(展宽不超过10%)的优化要求。 (3) 对初始种群得到的结果进行适应度评估,从种群中选择优良个体。 (4) 对次优个体进行交叉和变异运算。本文遗传算法在同一代中对各个个体采用不重复交叉和不重复变异的策略。即在同一代迭代中,对父代的那些可能发生交叉或者变异的个体,使其最多只能发生一次交叉或者变异。也就是让同一个父代个体不能多次进行交叉和变异。这有利于提高群体中各个个体的利用率,防止过早陷入局部最优解。进行自适应交叉概率和变异概率进行交叉和变异操作。 由于在迭代的初期,染色体的差异一般较大,交叉概率Pc大和变异概率Pm小有助于加快收敛;而在迭代的中后期,Pc小和Pm大有助于防止过早陷入局部最优点。因此,交叉概率Pc和变异概率Pm随迭代代数gen变化的表达式为 (9) (5)保存最佳个体,与交叉和变异操作前做比较,保留最佳值。 (6)满足程序停止条件后输出结果,程序流程图如图2所示[8-12]。 图2 遗传算法综合流程Fig.2 General flow chart of genetic algorithms 3实验仿真及性能分析 3.1仿真1 假设原线阵满阵共有阵元63个,其中有13个阵元由于损坏而不能参与工作,单个阵元的辐射特性为全向型和cosφ型 (φ为来波方向与天线阵法线方向的夹角)。遗传种群的个体数取为80,代数设为250,交叉概率为0.8,变异概率为0.07。仿真中,阵列中正常阵元位置和失效单元位置分别用蓝色O和红色X表征。 从图3中可以看出,对于阵元方向图为全向型,第一副瓣由无失效情况下的-13.25 dB变为-20.3 dB,波束宽度由3.6°变为3.95°,展宽约9%。优化后阵元位置为 [1,2,4,7,9,10,11,13,14,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,47,48,49,50,53,54,55,58,59,61,63]。图4 给出了波束扫描角分别为30°和-30°天线方向图的优化结果,同样具有较大的主旁瓣比。 对于图5阵元方向图为cosφ型来说,优化得到其最大副瓣值为-21.86 dB,算法在第238代达到最优,优化后阵元位置为 [1,2,5,8,10,12,14,15,16,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,53,55,57,58,59,61,63]。 从以上可以得知,阵列部分阵元失效导致主瓣宽度有所展宽,最高副瓣电平有所下降。为达到天线阵列失效情况下的更优水平,通过对失效单元的位置和波束宽度优化,波束在近区角度范围内维持了较低的副瓣电平,是以展宽主瓣和抬高远角副瓣电平的代价来换取主波束附近的低副瓣。 3.2仿真2 考察一个面阵,结合某相控阵雷达六边型阵面,设置其中有 10% 的阵元数为失效单元,初始种群个体数为120,代数为1 200。如图6所示,由于种群个体数和迭代次数选的比较高,算法在迭代过程中,趋势较为平滑。程序采用512×512点FFT法结合遗传算法对其阵元位置进行优化配置,优化参量选择其剖面方向图的副瓣和波束宽度,优化得副瓣最大值为-22.4 dB。 图3 全向型阵元阵列优化结果及其迭代过程Fig.3 Optimized results and evolution process of omnidirectional elements 图4 全向型阵元阵列扫描角为30°和-30°优化结果Fig.4 Optimized results of omnidirectional elements with 30° and -30° angle scan 图6 六边阵遗传算法迭代过程Fig.6 Evolution process of hexagon array 图6和图7分别给出了优化后的迭代过程以及阵元分布。图8为正弦空间中的立体方向图,坐标系中U=sinθcosφ,V=sinθsinφ,其中,θ和φ分别为俯仰角和方位角。 图7 六边阵失效位置优化结果Fig.7 Optimized results of failed elements in hexagon array 图8 六边阵优化后方向图Fig.8 Optimized pattern of hexagon array 仿真试验中,通过设置不同条件,得出不同的结果。 (1) 种群个体数为100,代数共有450代,交叉概率为0.8,变异概率为0.07,迭代到448代,主瓣宽度逼近良好,展宽约7%,第一副瓣值由-17.2 dB变为-20.2 dB,提高3.0 dB。 (2) 种群个体数为120,代数共有1 200代,交叉概率和变异概率相同,迭代到987代后趋于平缓,主瓣宽度展宽约8%。第一副瓣值由-17.5 dB变为-22.1 dB,提高4.6 dB。 以上结果一方面反映出遗传算法能较好地按照预期不断搜索最优值,没有过早地陷入局部最优值,在大型阵面的设计中具有一定的可行性;另一方面也反映出FFT法在计算中显著地提高了其优化效率。 4结束语 对阵元的位置优化是一个高度的非线性优化问题,很难采用解析的方法来求得其最优解,一般需要通过遗传算法、动态规划和模拟退火等智能算法求解其工程满意解。本文以典型线阵和面阵在一定数量阵元受损情况下的位置为优化对象,以波束近区副瓣和波束宽度(不超过10%)为约束标准,同时考虑到尽量降低远区副瓣。仿真结果表明,遗传算法都能达到预期要求,显著提高了阵列方向图的主副瓣比,具有较好的收敛性能和稳健性。 参考文献: [1]周志增,刘洪亮,顾荣军,等. 组件单元失效下的相控阵雷达暴露区研究[J]. 现代防御技术,2012,40(6): 140-144. ZHOU Zhi-zeng,LIU Hong-Liang,GU Rong-jun,et al. Phased Array Radar Detection Area when Its Module’s Element Fails[J]. Modern Defence Technology,2012,40(6): 140-144. [2]张光义.相控阵雷达系统[M]. 北京: 国防工业出版社,1994:298-317. ZHANG Guang-yi. Phased Array Radar System[M]. Beijing: National Defense Industry Press,1994:298-317. [3]杨丽娜,丁君,郭陈江,等. 基于遗传算法的阵列天线方向图综合技术[J]. 微波学报,2005,21(2): 38-41. YANG Li-Na,DING-Jun,GUO Chen-jiang,et al. Pattern Synthesis of Antenna Array Using Genetic Algorithm[J]. Journal of Microwaves,2005,21(2): 38-41. [4]汪茂光,吕善伟,刘瑞祥. 阵列天线分析与综合[M].西安:西安电子科技大学出版社,1989. WANG Mao-guang,LU Shan-wei,LIU Rui-xiang. Array Antenna Analysis and Synthesis[M]. Xi’an: Xidian University Press,1989. [5]Bassem R Mahafaza. 雷达系统分析与设计[M].北京:电子工业出版社,2008:303-304. Bassem R Mahafaza. Analysis and Design of Radar System [M].Beijing: Publishing House of Electronics industry,2008:303-304. [6]JOHNSON J M,RAHMAT-SAMII Y. Genetic Algorithm Optimization and Its Application to Antenna Design [C]∥Proceeding of the IEEE Antennas and Propagation International Symposium: IEEE Press,1994: 326-329. [7]王小平,曹立明. 遗传算法——理论、应用与软件实现[M].西安: 西安交通大学出版社,2002. WANG Xiao-ping,CAO Li-Ming. Genetic Algorithm- Theory, Application and Software Implementation[M].Xi’an:Xi’an Jiaotong University Press,2002. [8]马云辉. 基于遗传算法的唯相位控制方向图零点生成[J].微波学报,2001,17(2): 41-46. MA Yun-hui. Null Steering Using Genetic Algori-thms by Controlling Only the Current Phases[J]. Journal of Microwaves,2001,17(2): 41-46. [9]马云辉. 阵列天线的遗传算法综合. [J].电波科学学报,2001,16(2):172-176. MA Yun-hui. Synthesis of the Array Antennas Using Genetic Algorithm[J].Chinese Journal of Radio Science,2001,16(2):172-176. [10]任盛海,吴志忠. 遗传算法在阵列天线方向图综合设计中的应用[J].电波科学学报,1996,11 (4):62-67. REN Sheng-hai,WU Zhi-zhong. Application of Genetic Algorithm in Antenna Array Pattern Synthesis [J].Chinese Journal of Radio Science,1996,11(4):62-67. [11]梁宇宏,陈星,温剑,等.改进遗传算法应用于超低副瓣天线阵的综合设计[J].微波学报,2010,26(4):47-50. LIANG Yu-hong,CHEN Xing,WEN Jian,et al. An Improved Genetic Algorithm Applied in Pattern Synthesis of Ultra-Low Side Lobe Linear Array Antenna[J]. Journal of Microwaves,2010,26(4): 47-50. [12]SOLTANKARIM I F,NOURINIA J,GHOBADI C H. Side Lobe Level Optimization in Phased Array Antennas Using Genetic Algorithm [C]∥Spread Spectrum Techniques and Applications,2004 IEEE Eighth International Symposium,2004:389-394. Radiation Pattern-Reconstruction Based on Optimized Location of Failed Elements ZHOU Zhi-zeng,DING Gui-qiang,KANG Peng,GAO Feng-hua (Luoyang Electronic Equipment Test Center,Henan Mengzhou 454750, China) Abstract:Failed elements will destroy the array response. To reduce the impact, the genetic algorithm is used to optimize the failed location and an optimization model based on side-lobe as well as beam-width as the restricted standard is built. At the same time, by combining FFT (fast Fourier transformation) arithmetic, the amount of the computation is reduced. Simulation results show that the genetic algorithms can effectively improve the main-side-ratio of the array pattern and solve the problem of optimized array location in large array. Key words:element failure; side-lobe; wave beam width; genetic algorithms 中图分类号:TN958.92;TN82 文献标志码:A 文章编号:1009-086X(2015)-05-0129-06 doi:10.3969/j.issn.1009-086x.2015.05.022 通信地址:454750河南省孟州市066信箱111号E-mail:bravezhizeng@163.com 作者简介:周志增(1982-),男,安徽巢湖人。工程师,硕士,研究方向为电子对抗建模与仿真。 基金项目:有 *收稿日期:2014-06-16;修回日期:2014-08-22