端锚锚杆在不同预应力下的应力分布
2015-03-08王跃张毅
王 跃 张 毅
(北京科技大学土木与环境工程学院)
端锚锚杆在不同预应力下的应力分布
王 跃 张 毅
(北京科技大学土木与环境工程学院)
首先对全长粘接式锚杆和端锚锚杆的工作机理进行了探讨,总结了前人的研究成果,然后通过对端锚锚杆数值模拟,分析了端锚锚杆在加托盘预应力为0,10,60 kN时和不加托盘时的应力分布,揭示了端锚锚杆的应力分布规律,即随着预应力的增大,应力分布有往锚杆端部收缩的趋势,并且分析了在预应力为0 kN和60 kN的情况下,围岩表面相对不加锚杆时的位移分布,围岩表面相对位移集中在以锚杆锚固点为中心,1 m半径的范围内,锚固点相对位移值最大,并且在此范围内相对位移急剧减小。
端锚锚杆 应力分布 相对位移
随着采矿活动由露天逐渐转入地下,开始面临越来越多的地压显现,锚杆支护变得越来越重要。自从20世纪初在矿山工程中使用以来,到50年代,锚杆已经被广泛应用在岩石地下工程中[1]。尽管已经从锚杆试验和现场应用得到了很多关于锚杆支护的经验,但是由于锚杆在岩土介质中受力的复杂性,使得锚杆的作用机理依然存在多种说法。许多关于锚杆的设计计算依旧停留在经验上,或者是在过多假设的基础上,例如用弹性力学来求解具体的锚杆受力等。通过分析前人所做的工作,数值模拟出端锚锚杆在不同预应力情况下的受力特点,得出其应力分布规律,从而指导矿山支护工作。
1 不同锚杆支护理论
对于全长粘接式锚杆,已经有很多人做了受力分析。Freeman做了开创性工作[2],通过观测锚杆的受力过程及应力分布,提出了中性点和锚固长度的概念。郭军等为研究大断面黄土隧道中的系统锚杆作用[3],在Freeman中性点理论的基础上,通过理论推导,阐明了锚杆的作用机制,指出了浅埋大跨度黄土隧道中锚杆的受力原因,并采用理论单元模型,计算得到了与实测数据一致的结果。对于仅受拉拔荷载条件下的锚杆的受力分析,尤春安基于Mindlin问题的位移解[4],推导出全长粘接式锚杆的受力特征及其影响因素,为其力学分析和设计计算提供了理论依据。王志宏、刘雨田阐述了不同结构锚杆的受力机制与性能特征[5],由平衡条件推导出胶结式锚固结构的受力特征与性能特征,说明了发展复合式锚杆是提高锚杆技术性能,改善锚杆支护效果的有效与可靠的途径。杨双锁等采用数值模拟的方法[6],对拉拔状态和工作状态下的锚杆所受拉力和剪力的分布特征及演变规律进行了讨论,分别得出了全长锚固锚杆、端部锚固锚杆、无护表构件工作锚杆及有护表构件工作锚杆的拉应力和剪应力分布。
总的来说,对于全长粘接式锚杆,无论是根据平衡条件得到的解答还是由Mindlin问题推出的解答,都可以得出在拉拔作用力下所受的最大剪应力不是在孔口,而是在孔口附近的某一个位置,剪应力沿着锚杆迅速增大到这一最大值,然后逐渐地减小并且最终趋近于零,只不过在尤春安根据Mindlin问题的解答中,对于这一现象的解释是孔口单元体的剪应力互等。此外,根据王志宏的分析,若剪应力最大值达到了胶结剂的抗剪强度极限,那么破坏就将逐渐向上发展直至全长锚杆失效,这一分析结果也与杨双锁的数值模拟所观测到的结果相同。并且,这种破坏模式可以在杜润泽等的锚杆拉拔试验中得到证实[7],即在全长粘接式锚杆受拉时,并不是拉拔力达到最大时一次破坏的,而是在受力的过程中由外向里逐渐破坏。
对于端部拉拔锚杆,其与全长粘结式锚杆的拉拔受力相似,当锚杆各点的剪应力未达到极限时,剪应力和拉应力随深度的增大而逐渐减小,锚杆更深的部分不受力。当拉拔力增大到超过剪应力极限时,锚杆的端头部分会发生与粘结材料的相对滑动,此时,剪应力在端头部分先增大,到达最大值后又逐渐减小,拉应力逐渐减小。对于有端部结构的锚杆,端部结构使得最大锚固力的作用点外移,对于端锚时,锚固段锚杆相对于岩体具有外移趋势,因此,端锚时锚杆通常没有中性点的存在,并且,当端部的预应力过大时,全锚锚杆也不存在中性点。总的来说,有端部结构的锚杆与全长粘接式锚杆和无端部结构工作锚杆受力都不相同,其相当于两者应力分布的组合。
2 分析方法
运用数值模拟的方法分析端锚锚杆在不加托盘装置和施加托盘装置而预应力为0,10,60 kN的情况下,锚杆受力情况及锚固面的相对位移,揭示预应力对锚杆受力的影响。
数值模型尺寸为10 m×10 m×10 m,模型上部受到2 MPa的正压力来模拟地应力,模型的左右两侧、后侧和下侧固定。锚杆直径为25 mm,长6 m,其中锚固段长4 m,锚固位置为模型的正中间,锚固方向为从前向后。模型力学参数见表1。
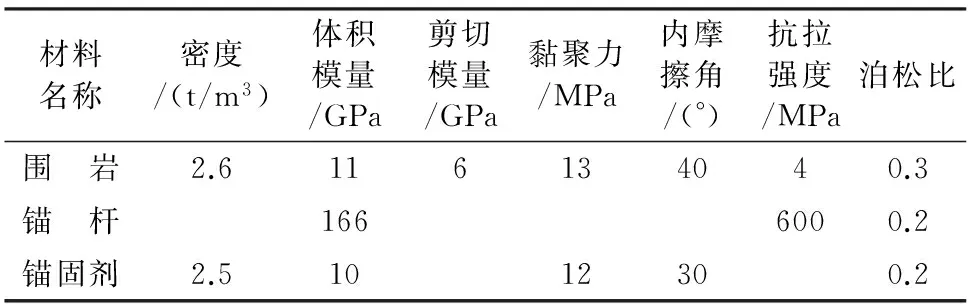
表1 模型力学参数
3 锚杆受力分析
保持地应力不变,分别调整参数模拟端锚支护不加托盘和施加托盘时的情况,在有托盘时,调节预应力的大小分别为0,10,60 kN,调取沿锚杆各节点的正应力和剪应力大小,并用曲线拟合,见图1。
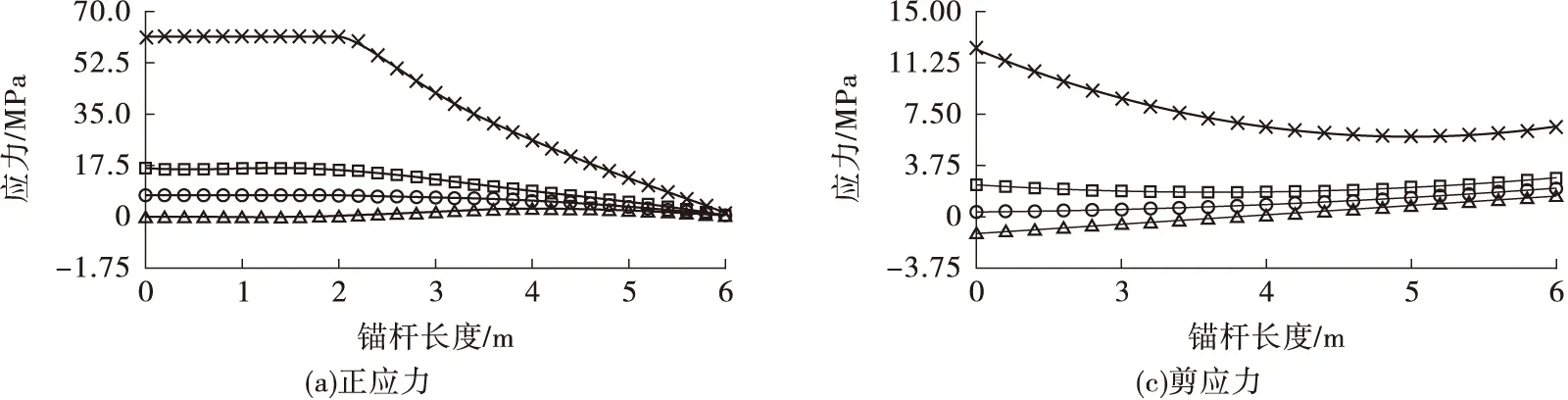
图1 锚杆应力分布
由图1可以看出,当锚杆不加托盘时,锚杆的受力分布和全锚时的受力分布几乎一样,正应力是先增大后减小,剪应力的方向相反,并且在锚固中点处出现一个中性点,此时锚杆所受到的拉力最大,而剪应力为零。
当锚杆加上托盘时,应力分布相对于无托盘时发生了显著的变化。中性点消失,正应力的分布沿锚杆胶结段逐渐减小,而剪应力都沿锚杆朝内分布,剪应力为零的点消失。当预应力为0 kN时,可以看到剪应力沿锚杆锚固段逐渐增大;当预应力为10 kN 时,剪应力沿锚固段先减小后增大;而当预应力为60 kN时,剪应力也是先减小后增大,但是锚杆末端的剪应力小于锚固始端的剪应力。总的来说,对于有托盘的锚杆,剪应力的最小值随着预应力的增大而逐渐向锚固深处移动。对于正应力来说,其降低的速度随着预应力的不同也不相同,具体表现为预应力越大,正应力在锚固段开始的一段内急剧降低,而后降低速度减小,在锚杆末端正应力最小。总体来说,随着预应力的增大,锚杆所受的正应力和剪应力有向锚固开始的地方集中的趋势。
4 端锚支护对岩体表面变形的影响
根据数值模拟得到锚杆锚固面的位移分布,以不加锚杆时的位移分布为基准,用端锚锚杆在不同预应力情况时的位移减去基准位移,得到相对位移分布。预应力为0和60 kN时的相对位移分布见图2。
从图2可以看出,当预应力为0 kN时,相对位移最大值产生在锚杆锚固的位置(X=0 m,Z=0 m),并且相对位移在以X=0 m,Z=0 m为中心,1 m 为半径的区域内集中,超出这个范围,相对位移变化很小;对于预应力为60 kN时,其相对位移也是集中在以锚杆锚固位置为中心,1 m为半径的区域内,超出此范围的相对位移迅速减小。锚杆支护在岩体表面上的影响范围集中在以锚固点为中心,半径为1 m的范围内,其影响范围可能与岩石的物理力学性质有关,与预应力的大小关系不大。
5 结 论
(1)端锚锚固没有托盘时,锚杆的应力分布和全锚无托盘时一样,都符合中性点理论。托盘的存在显著改变了应力分布,具体表现为随着预应力的增大,锚杆所受的正应力和剪应力有向岩体表面集中的趋势。
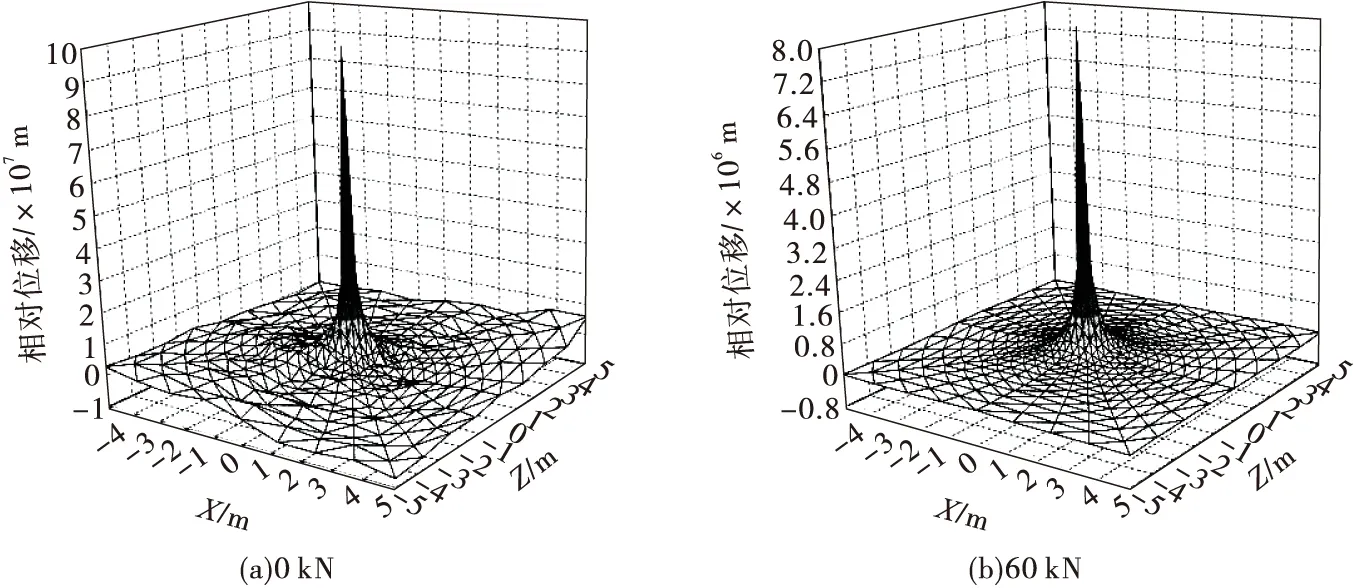
图2 不同预应力岩体表面的相对位移分布
(2)锚杆支护在表面上的影响范围集中在以锚固点为中心,半径一定的范围内,并且在此范围内迅速降低,超出此范围,相对变形就变得微乎其微,其影响范围可能与岩体的物理力学性质有关,而与预应力的大小关系不大。
[1] 郭小红,王梦恕.隧道支护结构中锚杆的功效分析[J].岩土力学,2007,28(10):2234-2239.
[2] Freeman T J. The behaviour of fully-bonded rock bolts in the Kielder experimental tunnel[J].Tunnels and Tunneling, 1978,10(7):37-40.
[3] 郭 军,王明年,谭忠盛,等.大跨浅埋黄土隧道中系统锚杆受力机制研究[J].岩土力学,2010,31(3):870-874.
[4] 尤春安.全长粘接式锚杆的受力分析[J].岩石力学与工程学报,2000,19(3):339-341.
[5] 王志宏,刘雨田.不同锚固方式锚杆受力机制与性能特征[J].矿冶工程,1994,14(2):17-20.
[6] 杨双锁,曹建平.锚杆受力演变机理及其与合理锚固长度的相关性[J].采矿与安全工程学报,2010,27(1):1-7.
[7] 杜润泽,明世祥,潘贵豪,等.全长粘接式锚杆锚固性能试验研究[J].煤炭工程,2009,41(1):74-76.
2014-08-07)
王 跃(1990—),男,硕士,100083 北京市海淀区学院路30号。
