一种优化的爆破振动回归计算方法
2015-03-08宁辉栋
宁辉栋
(内蒙古包钢钢联股份有限公司给水厂)
一种优化的爆破振动回归计算方法
宁辉栋
(内蒙古包钢钢联股份有限公司给水厂)
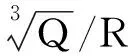
爆破振动 回归分析 数值分析 爆破安全
炸药在岩土介质中爆炸时,部分能量对周围的介质引起扰动,以波动形式向外传播,形成爆破振动。爆破振动波幅值通常用于表述振动强度,振动幅值指标有质点振动位移、振动速度、振动加速度。目前,许多国家采用质点振动速度作为振动强度的判据,这是因为大量的现场试验和观测表明,质点振动速度大小与爆破振动破坏程度的相关性最好,与传播地震波的岩土性质也有较稳定的关系[1-2]。
关于爆破振动波的衰减规律,前苏联科学家萨道夫斯基归纳出爆破地面振动经验计算公式,其与爆破最大段药量Q和爆心距R有关,并提出了与介质性质和爆源条件有关的系数K和衰减系数α。美国矿业局、奥特维尔、日本矿业会等也提出了与Q、R有关的衰减公式。实践中,一般根据已测的数据组,采用最小二乘法回归分析计算系数K和α,从而得出各区域的振动波衰减规律。然而,目前的爆破振动回归分析中,有50%的实际测点数据在回归线以上,直接采用回归公式作为安全判据存在较大安全隐患。本文以萨道夫斯基公式为例,提出安全性更高的回归计算方法[3-5]。
1 普通爆破振动回归方法
萨道夫斯基提出的爆破振动衰减公式为
(1)
式中,v为地面质点峰值振动速度,cm/s;Q为最大段药量,kg;R为观测点到爆源的距离,m;K,α分别为与爆点至观测点的地形、地质条件有关的系数和衰减系数。
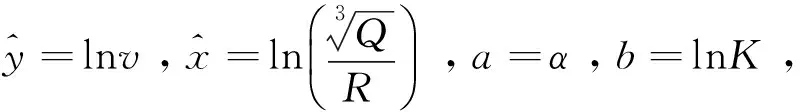
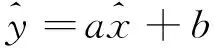
(2)
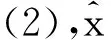
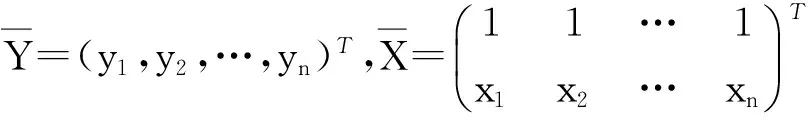
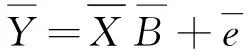
(3)
为了求得a和b,采用最小二乘法,寻找a和b的估计值a0和b0,使得方差Q(a0,b0)最小,其中
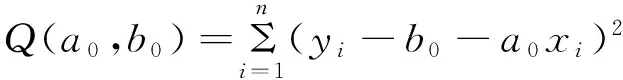
(4)
根据微积分求极值的原理,求得
(5)
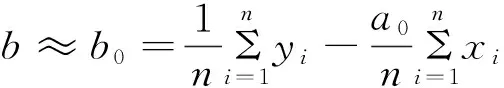
(6)
则
(7)
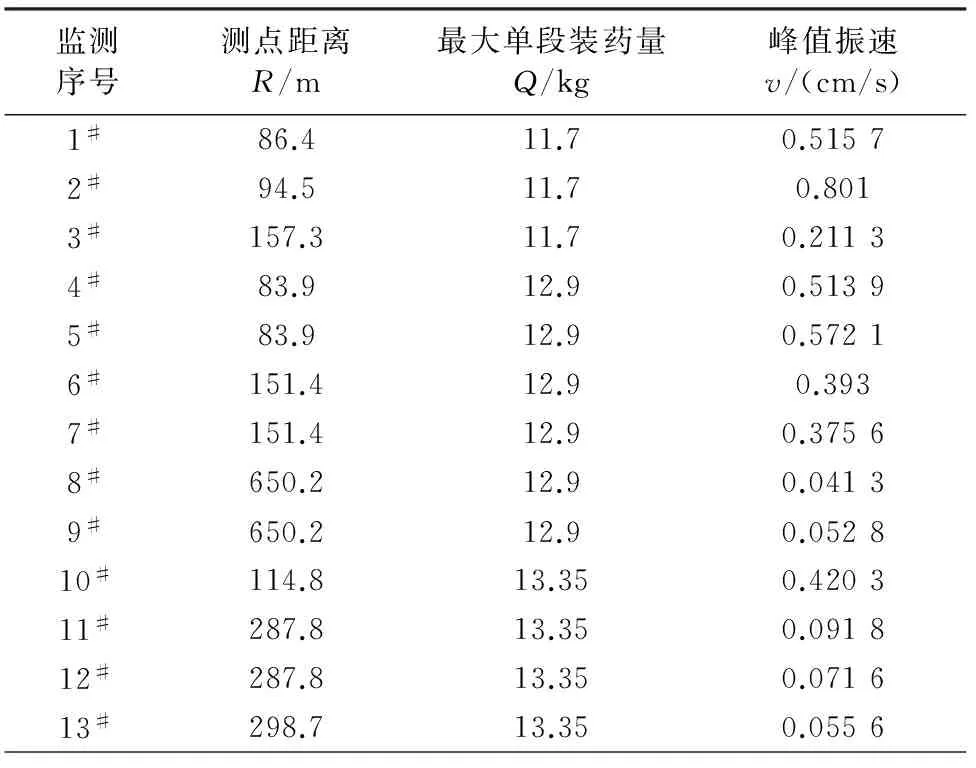
即为满足回归点集的回归线,位于实测样本点的中间,见图1。
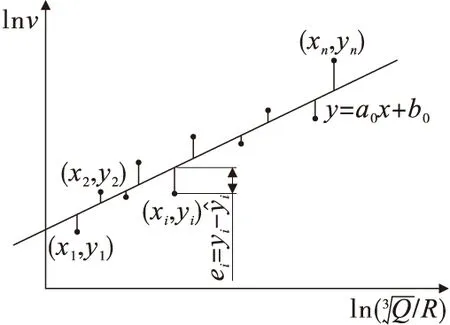
图1 回归线与数据样本点集图
2 优化的回归方法
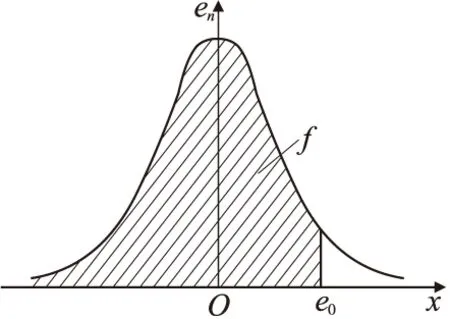
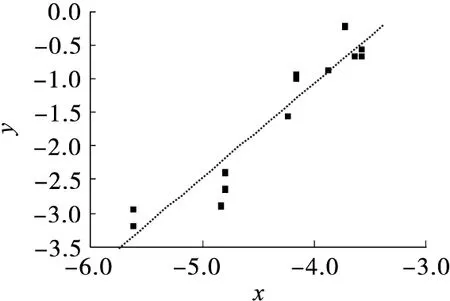
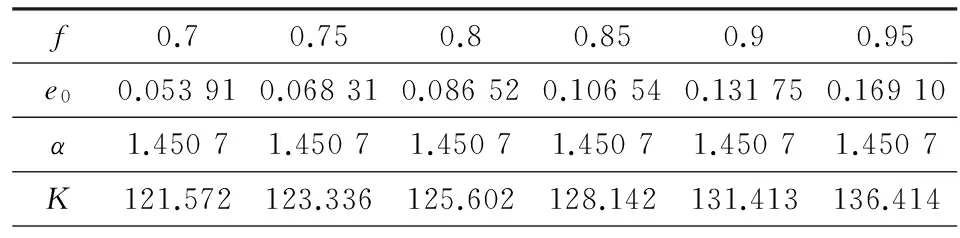
从图1可以看出,回归线以上有许多点,根据数理统计理论以及最小二乘法假设样本数据遵从正态分布,理论上有50%的样本数据点集满足yi>a0xi+b0,直接采用回归直线作为振动衰减规律是不安全的。因此提出安全因子f(0 (8) 式中,σ为e1,e2,...,en的标准差。 根据式(3),yi的离散分布情况与ei分布一致,回归线要满足安全因子f的要求,可以转化成e1,e2,...,en的回归线,满足f的要求,且y1,y2,...,yn回归线为 y=a0x+b0+e0, (9) 式中,e0为样本数据集e1,e2,…,en满足回归安全系数f条件的值,见图2。 图2 e0 和f位置关系 根据图2,可得 (10) 令U=x/σ,把式(10)转换成标准正态分布积分形式: (11) 查标准正态分布函数表,可求得各安全系数f对应的e0,表1列出了部分f值对应的e0。 表1 f值对应的e0 为了对比普通回归方程与加入安全系数f的回归方程,对某铁矿地下爆破振动进行了监测,取得13组监测数据,见表2。 表2 某铁矿爆破振动监测数据 采用普通回归方法回归得a0=1.450 7,b0=4.746 6,相关性系数r=0.937 6,回归线图见图3。 图3 回归线和回归点 相对应,α=1.450 7,K=115.193,即普通回归法得出的爆破振动衰减规律为 (12) 经计算,普通法回归的标准差σ=0.102 8。不同安全性系数f对应的e0、α、K见表3,f与α、K的关系见图4。 表3 不同安全性系数f对应的衰减系数 (1)针对普通回归方法理论上存在50%的数据大于回归方程得出的结果的情况,提出减少大于回归方程结果数据样本的对策,引入安全性系数f(0 (2)对普通回归方法残差加以统计分析,基于测试的爆破振动数据遵从正态分布的情况,推导出了不同安全系数f对应的残差适应值e0,进而得出α、K值。 (3)根据推导的回归方程和实例回归结果,f不影响衰减系数α,但系数K随f值增大而增大。 [1] 宗 琦,汪海波,周胜兵.爆破地震效应的监测和控制技术研究[J].岩石力学与工程学报,2008,27(5):938-945. [2] 何晓群.实用回归分析[M].北京:高等教育出版社,2008. [3] 国家安全生产监督管理总局.GB 6722—2003 爆破安全规程[S].北京:中国标准出版社,2004. [4] 汪旭光,于亚伦,刘殿中.爆破安全规程实施手册[M].北京:人民交通出版社,2004. [5] 全国统计方法应用标准化技术委员会.GB 4086.1-83 统计分布数值表正态分布[S].北京.中国标准出版社,1983. 2014-08-01) 宁辉栋(1963—),男,高级工程师,014010 内蒙古包头市河西工业园。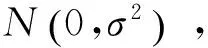
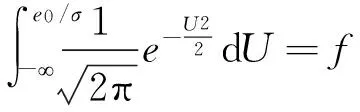

3 爆破振动回归对比
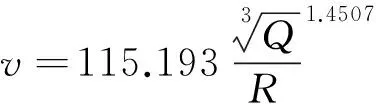
4 结 论
