一种高度冲突证据混合分步合成算法
2015-03-07黄丹丹
陈 强,黄丹丹,李 彬,卢 愿
(江西理工大学电气工程与自动化学院,江西 赣州341000)
ment,BPA),亦称基本信任分配。如果m(A)>0,则称A为焦元。对于相互独立的2个证据源 m1(*),m2(*),提供了如下经典合成公式:
一种高度冲突证据混合分步合成算法
陈 强,黄丹丹,李 彬,卢 愿
(江西理工大学电气工程与自动化学院,江西 赣州341000)
为证实证据分步合成方法在理论上的合理性,给出多证据分步合成结果的一般表达式,对分步合成方法理论上的合理性、合成结果的收敛性以及最终合成结果与证据行顺序之间的相关性进行研究。提出相关的定理和推论,并进行数学证明。针对高度冲突证据的分步合成问题,设计一种合成公式与加权平均法混合使用的分步合成算法。仿真结果表明,该算法的合成计算过程更为简洁,合成结果的收敛效果更好。
D-S证据合成;分步合成算法;收敛性;高度冲突证据;加权平均法
DO I:10.3969/j.issn.1000-3428.2015.10.057
1 概述
通常使用经典D-S证据合成公式合成2个高度冲突证据时,会得到有违常理的结果[1-2]。文献[3]提出一个著名的反例揭示这一问题。国内外学者已经提出了很多改进规则或算法。改进方案大体可分为2类:(1)规则修改方法;(2)证据修改方法。 文献[4]的改进措施是取消归一化因子,将冲突信息分配给不确定项。文献[5]提出了一种加权平均法则,具有明显的冲突消解效果。文献[6-9]提出的改进规则大体上将平均法与经典的D-S证据合成公式相结合,通过在各证据的平均信任分配之前增加一个加权系数的方法,实现对各焦元BPA的合理补偿。加权系数则是通过计算证据之间的相互支持程度或证据距离确定的[10-12]。文献[13]提出一种证据平均组合规则。首先,将各证据的可信分配平均分配给各焦元子集,然后使用经典合成规则对修改后的证据进行K-1次合成。文献[14]提出的改进方案是根据现实情况重新分配冲突的那部份信任分配。文献[15]提出一种证据修改规则,借鉴2个事件的联合概率实现证据信任分配的修改。这些改进方法具有程度不同的冲突消解效果,但它们也或多或少存
在各自的不足。如计算过程不够简捷,或合成结果的收敛性不够理想等。
本文提出一种较为简捷的冲突证据合成算法,即将经典合成公式和加权平均法混合使用的分步合成算法。尽管分步合成方法已被人们广泛使用,但该方法理论上的合理性目前尚未见诸文献探讨。因此,本文研究证据分步合成方法理论上的合理性问题,提出相关的定理和推论,并给出证明。
2 D-S证据合成法则及其分步合成方法
2.1 D-S证据合成法则
设空间Θ={χ1,χ2,…,χn}由一些互斥且穷举的元素组成,称为辨识框架。Θ的幂集2Θ形成一个命题集合,定义函数如果集合中的任一命题A(A∈2Θ)满足:

则称m为A的基本概率赋值(Basic Probability Assign-
ment,BPA),亦称基本信任分配。如果m(A)>0,则称A为焦元。对于相互独立的2个证据源 m1(*),m2(*),提供了如下经典合成公式:

其中,K值表示各项证据的相互冲突程度。当K=1时表示各方面证据极度冲突,无法进行证据合成。事实上,如果K>1,将使合成后的m(A)<0,同样无意义,因此,多个证据相互合成的先决条件是0<K<1,K值越接近1,表示证据之间的冲突程度越高。
2.2 证据分步合成方法
经典D-S证据合成公式只有两证据合成形式。当需要合成的证据超过2个时,普遍使用先将最前面的2个证据合成,然后逐步添加证据的分步合成方式。D-S证据合成公式满足结合律和交换律,但是,由于D-S证据合成公式无法用于高度冲突的证据合成,在很多实际问题合成过程中,常需要修改合成规则或证据本身。这就牵涉到证据顺序问题和分步合成在理论上的合理性问题,以及分步合成结果的收敛性及收敛条件等问题。
3 证据分步合成合理性及结果收敛性
本文提出关于D-S证据两两分步合成方法的定理和推论,并加以数学证明。
3.1 一般表达形式
首先,提出一个焦元子集互不相交条件下,分步合成最终合成结果的定理。
定理1 假设Θ为一识别框架,A为Θ中的焦元。设Θ中有 N个相互独立的 A的子集:A:A1,A2,…,AN,这些子集彼此互不相交。现有 n行相互独立的证据如下:

假定这些证据满足如下归一化条件:
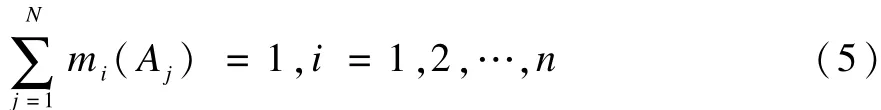
且任何两行证据之间的冲突程度K<1,如果使用文献[1]的合成公式对式(4)中的证据进行两两分步合成,那么最终的合成结果必为:

现在使用数学归纳法证明定理1,过程如下:
证明:首先获得最前2行证据的合成结果,这里,证据组数k=2,根据式(3),计算证据相互冲突程度:
N
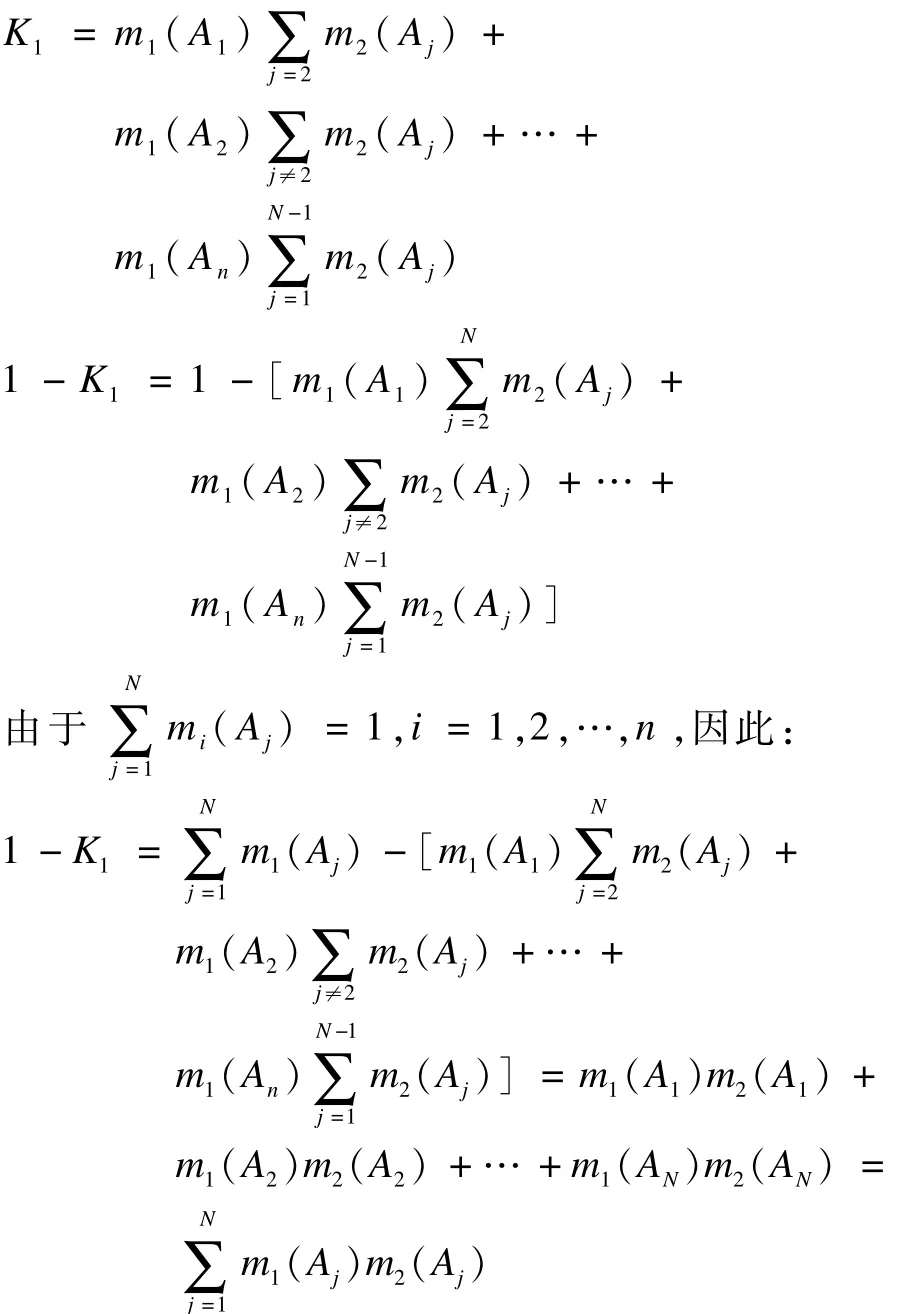
由式(2)得,第一步合成结果为:
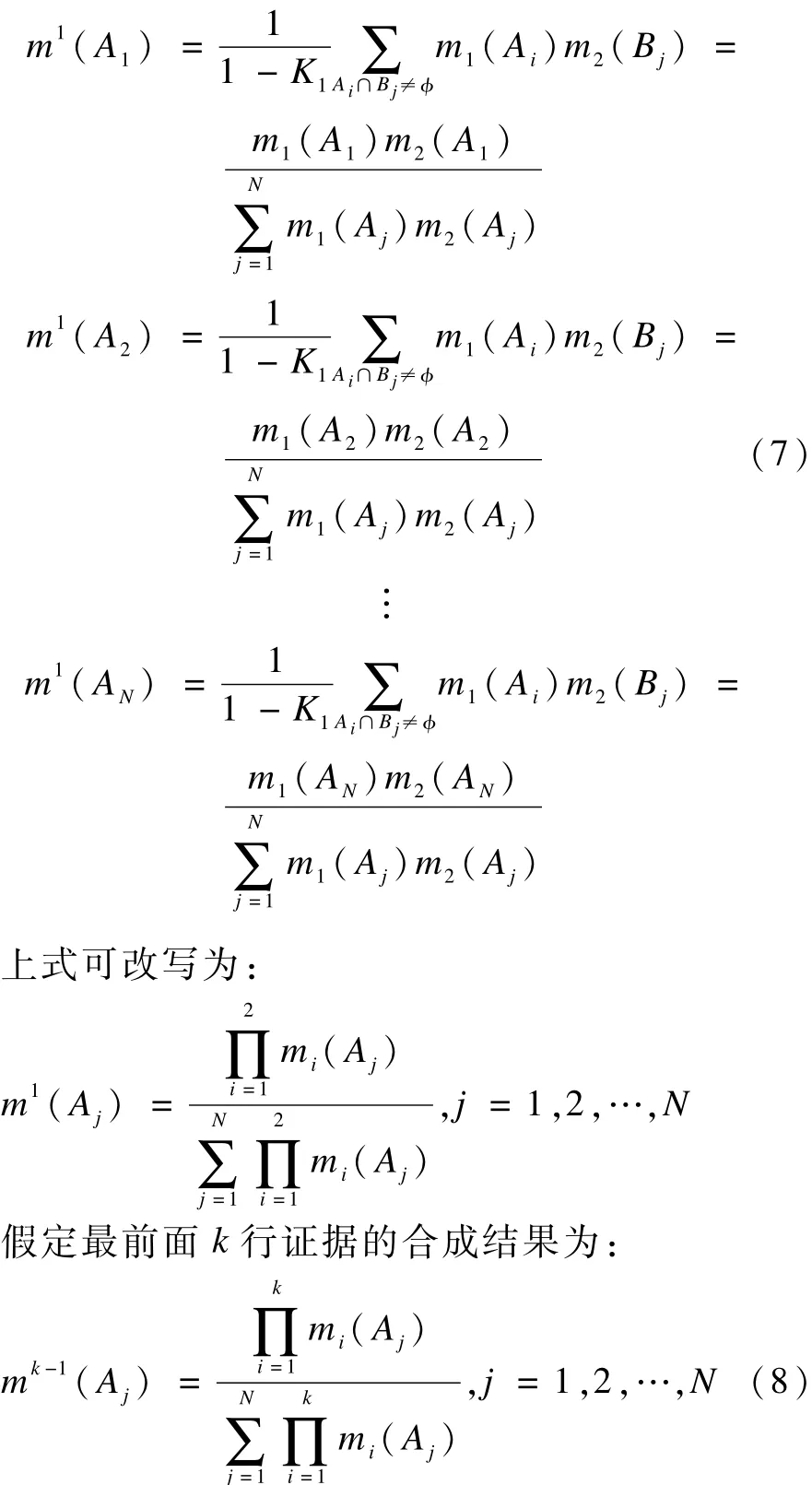
则可获得将式(8)中的结果与式(4)中下一行证据的合成结果。
冲突程度为:
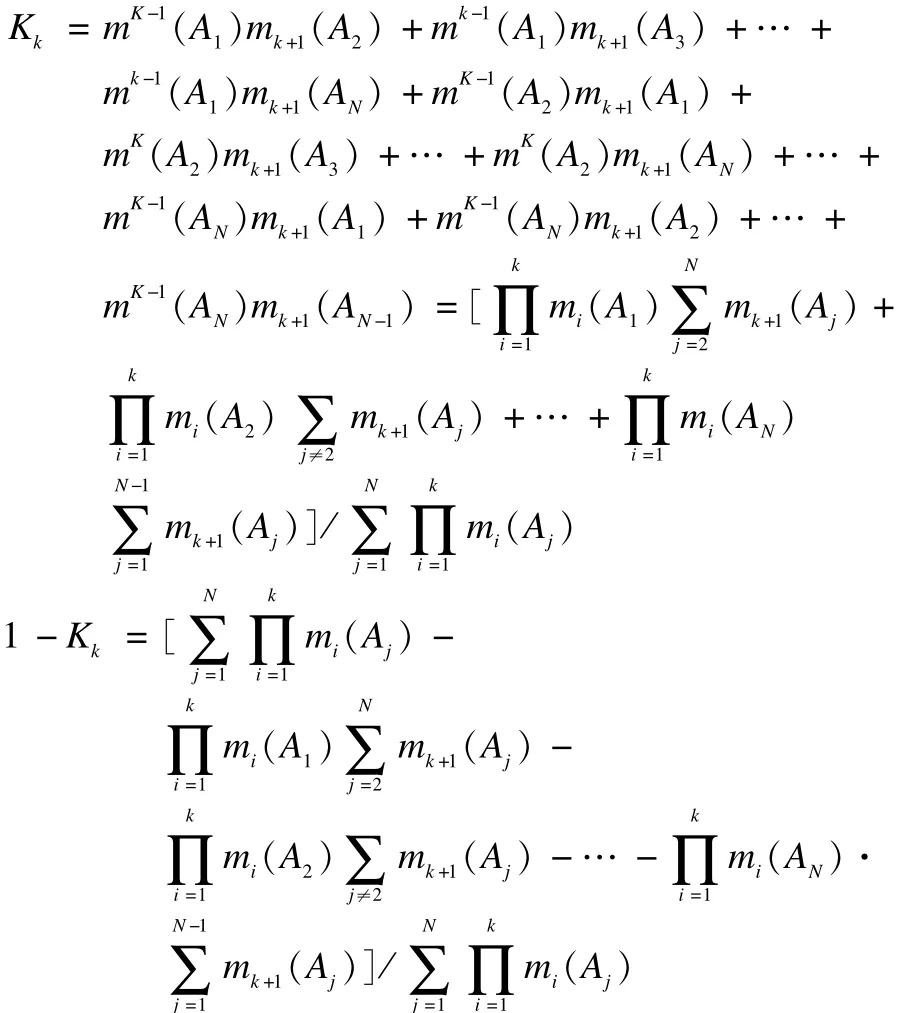
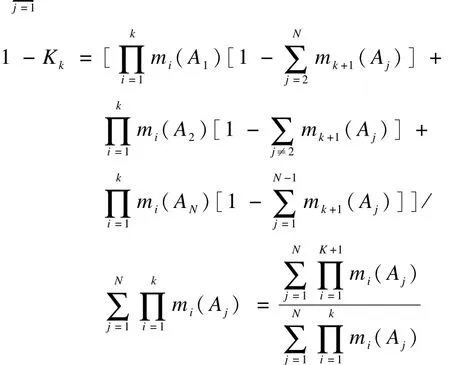
前K+1行证据的合成结果为:

由于全部证据的行数为n,即K+1可取的最大值为n,因此有:
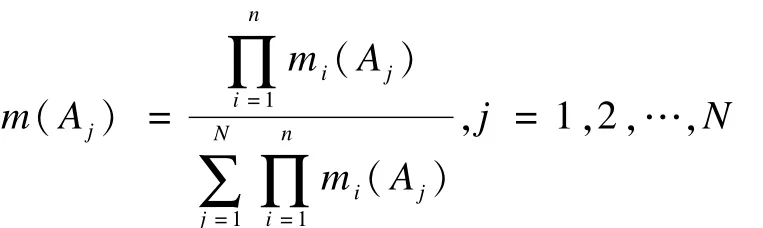
至此,定理1得证。
3.2 D-S证据分步合成结果的归一化问题
其次,提出一个关于使用前述合成方法所获得的合成结果满足归一化条件的定理。
定理2 假设Θ为一识别框架,A为Θ中的焦元。设Θ中有 N个相互独立的 A的子集:A:A1,A2,…,AN,这些子集彼此互不相交。现有 n行相互独立的证据如式(4)所示。假定这些证据满足归一化条件式(5),且任何2行证据之间的冲突程度K<1。如果使用文献[1]的合成公式对式(4)中的证据进行两两分步合成,最终合成结果可写作:
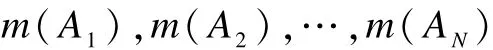
则这一合成结果满足如下归一化条件:

证明:依据定理1,最终合成结果中全部BPA之和为:
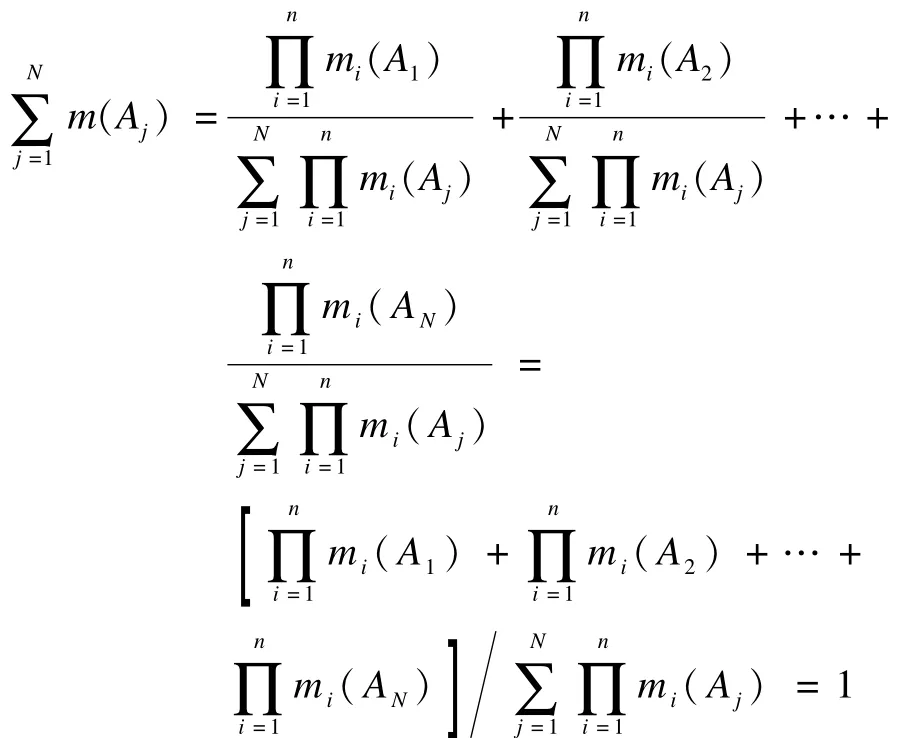
因此,定理2得证。
3.3 关于D-S证据两两分步合成方法的推论
依据定理 1和定理 2,还可以得出如下 2个推论:
推论1 使用文献[1]的合成公式以两两分步合成方式对式(4)中证据进行合成时其最终合成结果与式(4)中证据行的使用顺序无关。
证明:假如将式(4)中任意2行证据的位置互换,即将第k行证据mk(Aj)与第m行证据mm(Aj),j=1,2,…,N互换。设1≤k<m≤n。依据定理1中的结论,则式(4)中前k-1行证据合成结果为:
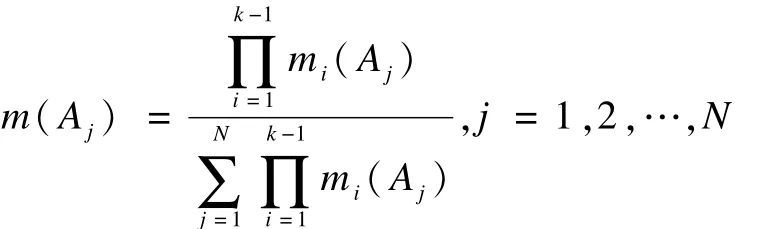

这一结果与定理1中未进行行交换时所得合成结果相同。因此,本推论得证。
推论2 使用文献[1]的合成公式以两两分步合成方式对式(4)中的证据进行合成时,如果在全部证据中至少存在一个焦元子集,其中的各BPA元素均不为0,写作:
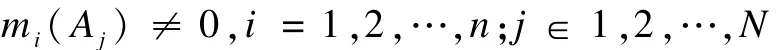
则最终合成结果必收敛,即,最终合成结果中,BPA分布必大部份集中到那些BPA元素均不为零的焦元子集。
证明:假定在证据式(4)的 n行证据中,其中的m行证据中至少存在一个为零的BPA元素。记作:
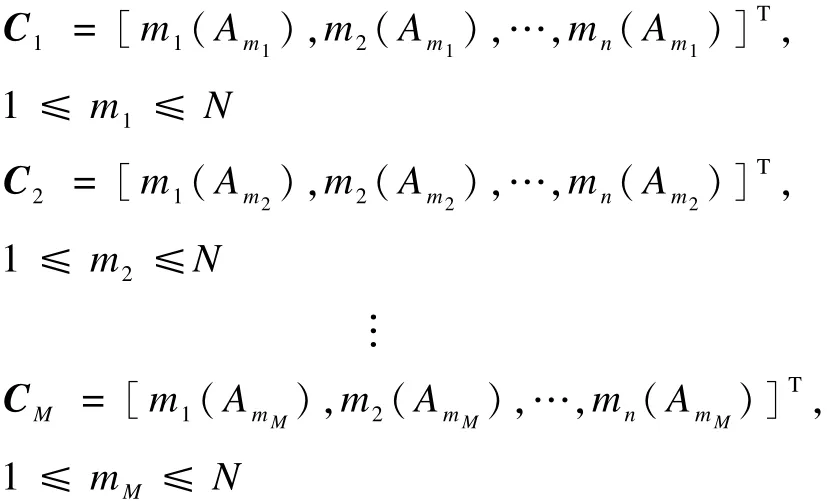
式(4)中其余P行证据中均无为零的BPA元素。 记作:

那么,有:
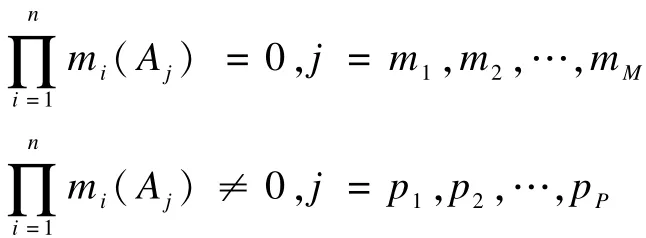
根据定理1,有:
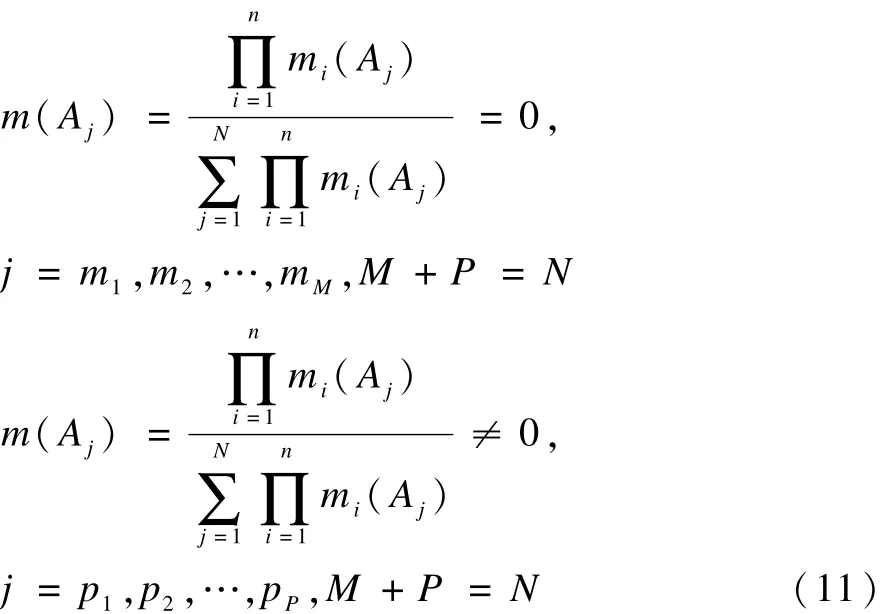
因此,在最终合成结果中,BPA的分配必集中到那些其中无为零 BPA元素的焦元子集。此推论得证。
4 改进的D-S证据合成算法
4.1 国内外学者提出的改进措施
针对高度冲突证据的合成问题,国内外学者提出了许多改进方法。文献[4]提出了一种改进方法,取消了D-S证据合成中的归一化因子,并将冲突信息全部赋予不确定项。虽然该方法可以避免极端的合成结果,但由于大多数信任分配给不确定项,在处理许多实际问题时,仍无法带来满意效果。文献[5]提出了加权平均算法,其合成公式如下:

权重由证据的可靠性或重要性决定。该方法可以较好地解决高度冲突证据合成问题,但其合成结果的收敛效果差一些。至于如何确定权重是一个需要进一步研究的问题。这种方法不适合单独使用,但可以与其他方法结合使用。文献[13]提出的改进方法是:首先求取各证据的平均可信分配,然后使用经典合成规则,反复使用先平均后合成的方法,对证据进行K-1次合成。该方法的计算过程较为繁复,合成结果的收敛性也需进一步改善。学者们分别提出了一些改进方法,合成结果得到不同程度的改善。大体结合经典的D-S方法和平均法。高度冲突证据合成时,更新BPA的主要部分来自BPA的平均值乘以一定的加权系数。加权系数则是通过计算证据之间的相互支持程度或证据距离确定的。这些方法可以避免传统D-S方法的一票否决现象或出现不合常理的结果。但现有大部分改进规则的计算过程比较复杂。如果加权平均方法只提供证据合成的中间结果,且最后合成结果能令人满意,则加权平均法可视作一种简单而有效的缓解冲突方法。因此,提出一种将经典D-S方法与加权平均法混合交替使用的新型合成算法。
4.2 分步合成算法
算法步骤如下:
Step1 根据设置的可信分配值上限(0.999 9)预处理所有的证据数据和,设置加权平均法的加权系数和冲突阈值kmax。
Step2 计算待合成的2个证据的冲突程度K。
Step3 如果k<kmax,使用合成公式式(2),否则选择加权平均法公式式(12)。
Step4 如果所有证据合成完毕,则保存最后结果并退出。否则,设置当前合成结果为第1个证据,提取下一个证据作为第2个证据等待合成,回到Step2。
关于冲突阈值如何确定的问题。在实际情况下,高度冲突证据与非高度冲突证据之间较难做出明确的区别。使用本文算法合成时,如果非高度冲突情况被视为高度冲突,可能降低合成结果的准确性。如果情况相反,将高度冲突视作非高度冲突,则可能无法得到融合结果。因此,宁愿非高度冲突情况被视为高度冲突,而不是相反。根据仿真结果,建议Kmax=0.96~0.98。
4.3 算法复杂度分析
将本文算法与经典合成公式相比,如果整个合成过程中冲突程度始终小于设定的阈值,则两者合成计算过程大体相同。算法复杂度决定于子集数N和证据行数n。一般使N≤6,n≤6,可合理控制算法的硬件开销和时间复杂度。如果合成过程中存在高度冲突证据(K≥Kmax),此时选用加权平均合成公式式(12),其算法复杂度小于合成公式。因此本文算法与经典合成公式相比,复杂度无明显增大。
5 仿真结果和分析
本文收集了5组从某煤矿瓦斯监测系统提取的冲突样本数据,如表1所示。这些样本代表5种经常出现在煤矿井下的不同情况(1个正常样本和4个异常样本)。分别使用经典的D-S证据合成方法、国内外代表性的改进方法和本文算法进行合成有效性对比测试。测试结果如表2所示。
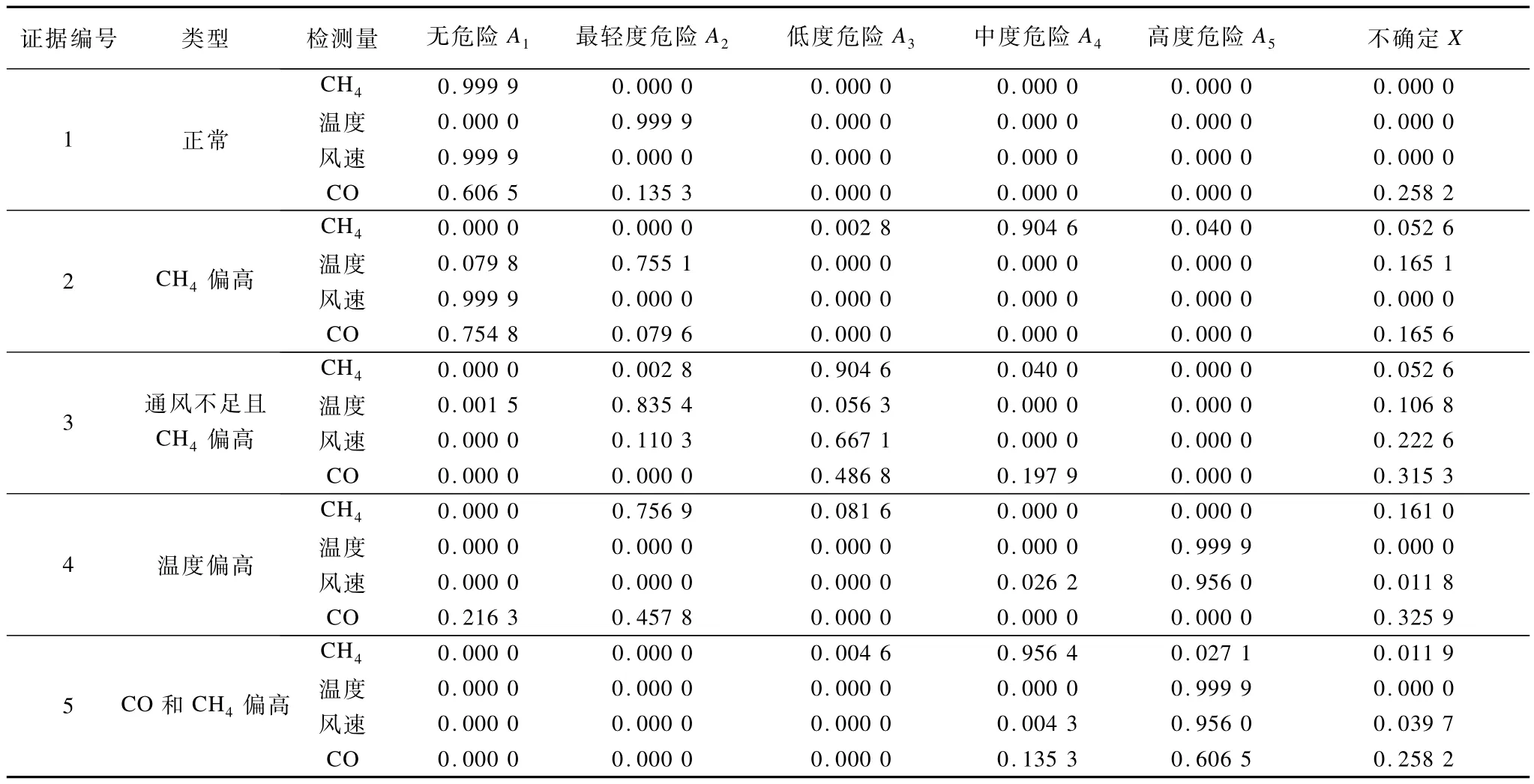
表1 证据样本与危险等级对应的BPA值
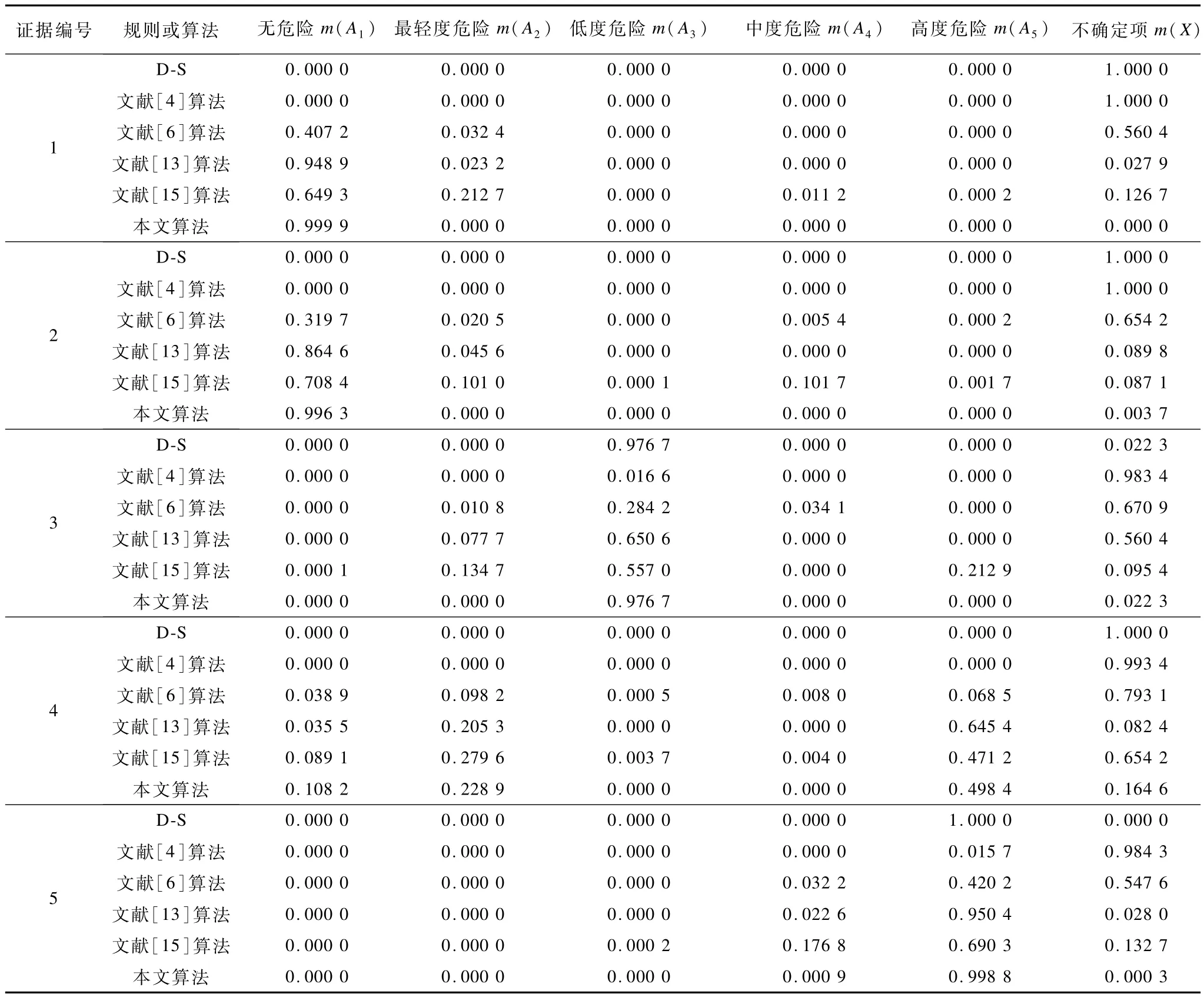
表2 5种不同冲突程度证据合成结果的对比
测试结果表明:
(1)在多数情况下,本文算法的最终合成结果比表中列出的代表性改进规则具有更好的收敛效果和较小的不确定性。
(2)在证据4的合成中,出现了不够收敛的合成结果。出现此结果的原因是,在最后一步合成中,加权平均法被选用。可见,使用本文算法时,应尽量避免在最后一步使用加权平均法。如果将证据行2和行3互换,最后合成结果将是A1=0,A2=0,A3=0,A4=0,A5=0.992 3,X=0.007 3。这使合成结果的收敛效果得到了明显改善。因此,可通过适当调整证据顺序改善合成结果的收敛性。此外,可以合理地调整加权平均法的加权系数来改善合成效果,并使合成结果更符合工程实际。
6 结束语
为解决高度冲突证据的分步合成问题,本文提出一种合成公式与加权平均法混合使用的分布合成算法。理论研究和仿真结果表明:分步合成方法具有理论上的合理性,且分步合成结果具有收敛性。本文提出的冲突证据合成算法合成高度冲突证据时,合成结果比其他改进规则具有更好的收敛效果和更小的不确定性。使用该算法合成高度冲突证据时,如果最后一步选用平均法,可能会使合成结果的收敛性变差。但如果适当调整证据顺序,可明显改善合成结果的收敛性。因此,下一步工作需要对此进行研究。
[1] Dempste A.Upper and Lower Probabilities Induced by a Multivalued Mapping[J].Annals of Mathematical Statistics,1967,38(2):325-339.
[2] Shafer G.A Mathematical Theory of Evidence[M]. Princeton,USA:Princeton University Press,1976.
[3] Zadeh L.A Simple View of the Dempster-Shafer Theory of Evidence and Its Implication for the Rule of Combination[J].A I Magazine,1986,7(2):85-90.
[4] Yager R R.On the Dempster-Shafer Framework and New Combination Rules[J].Information Sciences,1987,41(2):93-137.
[5] Person S,Kreinovich V.Representation,Propagation and Aggregation of Uncertainty[Z].2002.
[6] 孙 全,叶秀清,顾伟康.一种新的基于证据理论的合成公式[J].电子学报,2000,28(8):117-119.
[7] 李弼程,王 波,魏 俊,等.一种有效的证据理论合成公式[J].数据采集与处理,2002,17(1):33-36.
[8] 邓 勇,施文康.一种改进的证据推理组合规则[J].上海交通大学学报,2003,37(8):1275-1278.
[9] 肖明珠,陈光禹.一种改进的证据合成公式[J].数据采集与处理,2004,19(4):467-469.
[10] 潘 恺,李 辉,邢 钢.基于置信距离的冲突证据合成方法[J].计算机工程,2013,39(1):290-293.
[11] 权 文,王晓丹,王 坚,等.一种基于局部冲突分配的 DST组合规则[J].电子学报,2012,40(9):1880-1884.
[12] 董增寿,邓丽君,曾建潮.一种新的基于证据权重的DS改进算法[J].计算机技术与发展,2013,23(5):58-62.
[13] Murphy C K.Combining Belief Functions when Evidence Conflicts[J].Decision Support System s,2000,29(1):1-9.
[14] Lefevre E,Colot O,Vannoorenberghe P.Belief Function Combination and the Conflict Management[J]. Information Fusion,2002,3(2):149-162.
[15] Ali T,Dutta P,Boruah H.A New Combination Rule for Conflict Problem of Dempster-Shafer Evidence Theory[J]. International Journal of Energy,Information and Communications,2012,3(1):35-40.
编辑顾逸斐
A Mixed Step by Step Combination Algorithm for Highly Conflict Evidence
CHEN Qiang,HUANG Dandan,LI Bin,LU Yuan
(School of Electrical Engineering and Automation,Jiangxi University of Science and Technology,Ganzhou 341000,China)
In spite of step by step combination method is widely used by researchers,the rationality of this method in theory is not appeared in the literature review.This paper presents a general math expressions of step by step combination results,and studies the theoretical rationality of step by step combination method.The convergence of the combination results,the relationship between final combination results and the row order is studied.Several theorems and deductions are presented and proved using mathematical methods.The step by step combination algorithm mixing evidence combination formula and the weighted average method is proposed for combination of highly conflict evidence. Simulation results show that the proposed algorithm has simpler calculation process and better convergence effectiveness than representative alternative rules.
D-S evidence combination;step by step combination algorithm;convergence;highly conflict evidence;weighted average method
陈 强,黄丹丹,李 彬,等.一种高度冲突证据混合分步合成算法[J].计算机工程,2015,41(10):302-308.
英文引用格式:Chen Qiang,Huang Dandan,Li Bin,et al.A Mixed Step by Step Combination Algorithm for Highly Conflict Evidence[J].Computer Engineering,2015,41(10):302-308.
1000-3428(2015)10-0302-07
A
TP301.6
江西省教育厅科学技术研究基金资助项目(GJJ13398);江西省研究生创新专项基金资助项目(YC2013-S195)。
陈 强(1964-),男,教授、博士,主研方向:信息融合,智能监测,人工免疫;黄丹丹、李 彬、卢 愿,硕士研究生。
2014-09-28
2014-12-01E-m ail:ls6400@126.com
