一种基于复数编码的果蝇优化算法

陆民迪，周永权，黄 慷

（1.广西大学计算机与电子信息学院，南宁 530004；2.广西民族大学信息科学与工程学院，南宁 530004）

一种基于复数编码的果蝇优化算法

陆民迪1，周永权2，黄 慷1

（1.广西大学计算机与电子信息学院，南宁 530004；2.广西民族大学信息科学与工程学院，南宁 530004）

针对果蝇优化算法易陷入早熟收敛和寻优精度不高的缺点，提出一种基于复数编码的果蝇优化算法。引入复数编码的双倍体思想，目标函数自变量的大小由其相对应的复数的模决定，自变量的符号由相对应的复数的幅角决定。对9个基准测试函数进行对比实验，结果表明，与实数编码的果蝇算法相比，复数编码的果蝇算法拓展了个体基因的信息量，增加了种群的多样性。

果蝇优化算法；双倍体；实数编码；复数编码

DO I：10.3969/j.issn.1000-3428.2015.10.034

1 概述

群智能优化算法是近年来新兴的一种优化方法，愈来愈受到人们的极大关注，逐渐成为人工智能、计算机科学技术等交叉领域的前沿研究和热点方向。群智能优化算法的机理源于其模拟自然界、人类社会等动物的各种群体行为，利用群体之中个体之间的信息交互和合作实现寻优的目的。与其他类型的优化方法相比，其算法原理简单、实现方便、效率高。如遗传算法（Genetic Algorithm，GA）［1］、粒子群优化（Particle Swarm Optimization，PSO）算法［2］、萤火虫算法（Firefly Algorithm，FA）［3］、群搜索优化（Group Search Optimization，GSO）算法［4］、布谷鸟搜索（Cuckoo Search，CS）算法［5］、谐声搜索（Harmony Search，HS）算法［6］、蝙蝠算法（Bat-inspired Algorithm，BA）［7］，动物迁徙优化（Animal Migration Optimization，AMO）算法［8］和人工蜂群（Artificial Bee Colony，ABC）算法［9］等。目前群智能优化算法作为一种新兴的基于群体智能的启发式算法，已被广泛地应用于工程技术、军事科技、网络通信、金融、自动控制、资源分配、经济管理等许多优化领域。

果蝇优化算法（Fruit fly Optimization Algori-thm，FOA）［10］是由台湾学者潘文超在2011年提出的一种基于果蝇觅食行为的新的全局优化进化算法。相比于其他一些群智能优化算法，果蝇算法拥有简单、参数少、易调节、寻优精度较高等优点，因此，越来越被

国内外学者所关注，逐渐发展成为群智能优化领域的又一主流算法。目前，果蝇优化算法已经成功应用于许多方面，例如微调Z-SCORE模型系数、广义回归神经网络参数优化、灰色神经网络参数的优化等［11-12］。初始参数的选取以及搜索步长的限制使得该算法存在不足，例如容易陷入局部最优值、寻优精度不高等。

本文针对果蝇优化算法（FOA）易陷入早熟收敛和寻优精度不高等缺点，提出一种基于复数编码的果蝇优化算法（Complex-valued Fly Optimization Algorithm，CFOA）。该算法利用双倍体来表达基因，拓展了染色体的信息容量。复数的幅角决定自变量的符号，尽管复数的实部和虚部仍然由实数表示，但与传统的实数编码相比，该算法以实部和虚部2个变量来表示一个自变量，信息量扩大了2倍，增强了群体的信息，挖掘群体中个体的多样性，减少了局部收敛［13］。

2 实数编码果蝇优化算法

基本果蝇优化算法即实数编码果蝇优化算法是一种基于模拟果蝇觅食行为提出的新的全局搜索优化算法。自然界果蝇主要以腐烂的水果为主食，如人类栖息地果园、菜市场等皆可见其踪迹。这是因为果蝇拥有优于其他物种的嗅觉和视觉，能利用嗅觉快速飞近食物，通过敏锐的视觉发现食物与同伴聚集的位置，并往该方向飞去。模拟果蝇搜寻食物的行为过程，对果蝇优化算法数学模型的描述可归纳为如下步骤：

步骤1 随机初始果蝇群体位置：Init X-aχis，Init Y-aχis。

步骤2 赋予果蝇个体利用嗅觉搜寻食物的随机方向与距离：

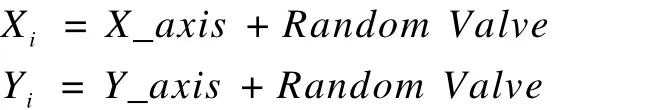
步骤3 由于无法得知食物的位置，因此先估计与原点的距离（Dist），再计算味道浓度判定值（S），此值为距离的倒数：

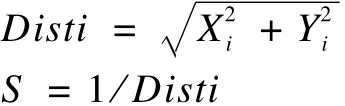
步骤4 将味道浓度判定值（S）代入味道浓度判定函数，以求出该果蝇个体位置的味道浓度（Smelli）：

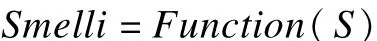
步骤5 找出果蝇群体中味道浓度最高的果蝇（求极大值）：

步骤6 保留最佳味道浓度值与χ，y坐标，此时果蝇群体往该位置飞去：

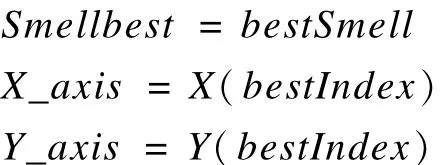
步骤7 进入迭代寻优，重复执行步骤2～步骤5，并判断味道浓度是否优于前一次迭代味道浓度，若是则执行步骤6。

3 复数编码果蝇优化算法

基本果蝇优化算法是基于二维空间设计的，位置由X和Y方向来决定。对于一个含有M个自变量的函数优化问题，设有2M个复数，前M个复数对应果蝇在X方向的位置，后M个复数对应果蝇在Y方向的位置，分别记为：

则果蝇的基因可表示为双倍体，记为：（（Rχ，Ry），（Iχ，Iy）），式（1）、式（2）中Rχk，Ryk分别表示果蝇在X和Y方向分量上第k维的实部；Iχk和Iyk分别表示果蝇在X和Y方向分量上第k维的虚部。故果蝇i结构可表示成如图1所示。

图1 果蝇染色体的结构

3.1 果蝇群体初始化

设函数自变量的范围为区间［AL，BL］，L=1，2，…，2M，随机产生2M个模和2M个幅角，产生的模向量满足以下关系：

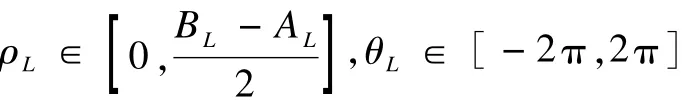
L=1，2，…，2M构成2M个复数，即：

将这2M个实部和2M个虚部按照实验选取的标准测试函数分配果蝇在X和Y方向的位置，产生一个果蝇群体。

3.2 果蝇群体的位置更新

实部更新为：

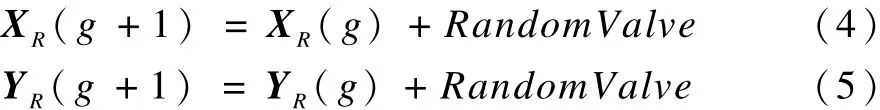
其中，XR（g）表示第g次迭代后果蝇在X方向上位置的实部；YR（g）表示第g次迭代后果蝇在Y方向上位置的实部。

虚部更新为：

其中，XI（g）表示第g次迭代后果蝇在X方向上位置的虚部；YI（g）表示第g次迭代后果蝇在Y方向上位置的虚部。

3.3 适应度计算

为求解适应度函数，必须将复数果蝇转换成实数果蝇，以复数的模作为实数值的大小，其符号由幅角决定，具体如下：

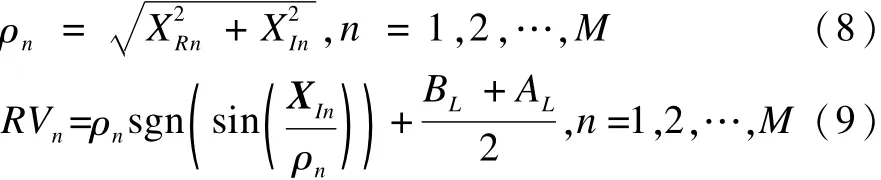
其中，ρk为第k维变量的模；XRn和XIn分别为第k维变量的实部和虚部；RVn为转换后的实数自变量。

3.4 复数编码果蝇优化算法步骤

复数编码果蝇优化算法步骤如下：

步骤1 随机产生2M个模和2M个幅角，并利用式（3）将果蝇初试位置用实部和虚部表示。

步骤2 利用式（4）～式（7）对果蝇的实部位置和虚部位置进行更新。

步骤3 利用式（8）～式（9）将复数果蝇转换成实数果蝇。

步骤4 执行FOA算法步骤3～步骤5。

步骤5 保留最佳味道浓度值与χ，y实部和虚部坐标，此时果蝇群体利用视觉往该位置飞去。

步骤6 进入迭代寻优，重复执行步骤 2～步骤5，并判断味道浓度是否优于前一次迭代味道浓度，若是则执行步骤5。

4 实验结果与分析

为了验证CFOA的有效性，选取了9个基准测试函数进行性能测试，如表1所示。

表1 实验选取的标准测试函数

9个函数均为30维的函数，且9个函数的最优值均为最小值0，其中，f1～f6为单峰高维函数；f7～f9为多峰高维函数。

4.1 实验环境

在Matlab R2012b中进行编程，数值实验在Intel酷睿2双核T6600处理器、2 GB内存上进行。

4.2 参数设置

FOA和CFOA的参数设置是一致的。种群数量为30，迭代次数为600。

4.3 实验结果对比

分别用2种算法对9个函数进行20次实验，实验中所得到的最好适应度值、最差的适应度值、平均适应度值以及实验的平均方差如表2所示。

表2 2种算法对函数f1～f9的测试结果

由表2结果可以看出，对于单峰函数f1～f6，复数编码果蝇算法相比实数编码果蝇算法能获得较好的适应度值、平均适应度值、标准差，在最坏适应度值上，复数编码果蝇算法的表现也更好。如f1中，从2种算法的比较结果可以看出，实数编码算法可以获得不错的最优值，但是从平均适应度值看，结果并不理想，说明实数编码算法易陷入局部最优值，而从复数编码算法的实验结果上看，最优值与平均值相差无几，说明复数编码算法较实数编码算法更稳定。对于多峰函数f7～f9，复数编码算法比实数编码算法能获得较好的适应度值、平均适应度值。在f8和f9中，复数编码算法都优于实数编码算法，在f7中，最优值上，复数编码算法虽然优于实数编码算法，但是从平均值来看，复数编码算法和实数编码算法一样也都陷入了局部最优，所以均值较最优值增大了不少。总的来说，复数编码双倍体的思想以实部和虚部2个变量来表示一个自变量，增强群体的信息，挖掘群体中个体的多样性，增加了种群多样性，提高了算法的收敛速度以及收敛精度，减少了可能陷入局部最优。

图2～图5分别是2种算法对函数f1，f5，f8，f9的适应度函数进化曲线图（为了方便进化曲线的显示和观察，对适应度取以10为底的对数）。对于单峰函数f1，f5，复数编码方法不仅以较快的速度收敛，而且收敛精度明显优于实数编码方法。且从方差来看，稳定性更强，说明改善了FOA易陷入局部最优的缺点。对于多峰函数f8和f9，复数编码果蝇算法在收敛速度、收敛精度上也优于实数编码果蝇算法。

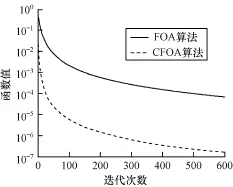
图2 函数f1的适应度函数进化曲线

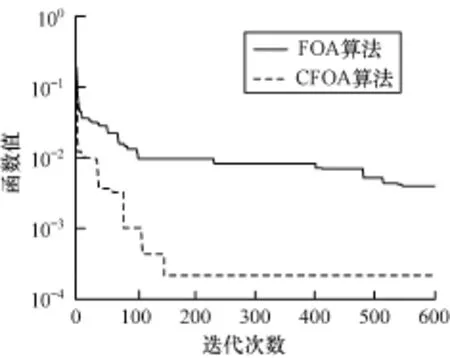
图3 函数f5的适应度函数进化曲线

图4 函数f8的适应度函数进化曲线

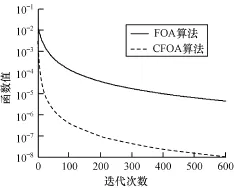
图5 函数f9的适应度函数进化曲线

表3是CFOA和FOA在1 000维数下，分别对单峰函数f1，f3和多峰函数f5，f8，f9进行20次实验的结果。由实验结果可以看出在这5个函数中，CFOA的最好适应度值、最差适应度值、平均适应度值以及平均方差全都优于FOA。说明CFOA同样可以在高维下，较FOA得到更优的适应度值，且稳定性也较好。

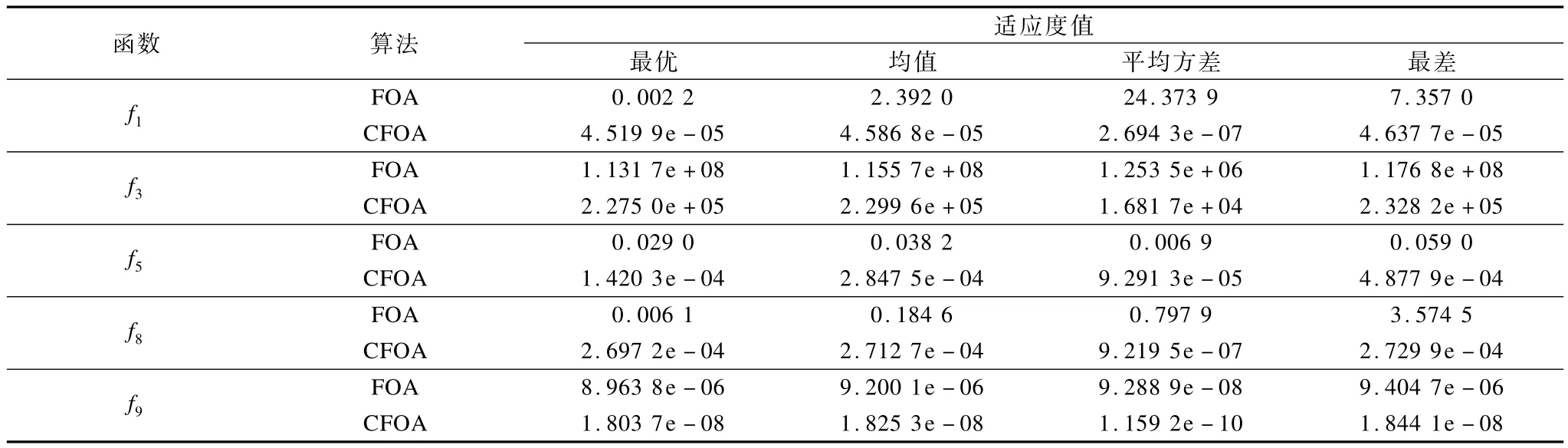
表3 CFOA和FOA在高维下的实验结果比较

5 结束语

本文提出了一种基于复数编码的果蝇优化算法。引入双倍体思想，拓展了染色体的信息容量，由于复数固有的二维特征，一个自变量由实部和虚部2个部分表示，使得每一个复数所能表达的信息量要比实数所表达的信息量多 2倍，增强群体的信息，挖掘群体中个体的多样性，从而使算法对全局最优的搜索能力得到改善，并减少了局部收敛，实验结果表明了该算法的有效性。目前果蝇优化算法在实际应用中还比较少，今后的研究方向侧重于将果蝇优化算法更多地应用于 TSP、车辆路径调度等领域。

［1］ Holland JH.Adaptation in Natural and Artificial System s［M］.Cam bridge，USA：MIT Press，1992.

［2］ Kennedy J，Eberhart R.Particle Swarm Optimization［C］//Proceedings of International Conference on Neural Networks.Washington D.C.，USA：IEEE Press，1995：1942-1948.

［3］ Yang Xinshe.Multiobjective Firefly Algorithm for Continuous Optimization［J］.Engineering with Computers，2013，29（2）：175-184.

［4］ He S，W u Q H，Saunders JR.Group Search Optimizer：An Optimization Algorithm Inspired by Animal Searching Behavior［J］.IEEE Transactions on Evolutionary Computation，2009，13（5）：973-990.

［5］ Yang Xinshe，Deb S.Cuckoo Search via Levy Flights［C］// Proceedings of World Congress on Nature&Biologically Inspired Computing.Washington D.C.，USA：IEEE Press，2009：210-214.

［6］ Geem Z W，Kim JH，Loganathan G V.A New Heuristic Optimization Algorithm：Harmony Search［J］.Simulation，2001，76（2）：60-68.

［7］ Yang Xinshe.A Nature-inspired Metaheuristic Batinspired Algorithms［M］.Frome，UK：Luniver Press，2010.

［8］ Li Xiangtao，Zhang Jie，Yin Minghao.Animal Migration Optimization：An Optimization Algorithm Inspired by Animal Migration Behavior［J］.Neural Computing and Applications，2014，24（7/8）：1867-1877.

［9］ Karaboga D，Basturk B.A Powerful and Efficient Algorithm for Numerical Function Optimization：Artificial Bee Colony（ABC）Algorithm［J］.Journal of Global Optimization，2007，39（3）：459-471.

［10］ 潘文超.果蝇最佳化演算法［M］.台北：沧海书局，2011.

［11］ 史东亚，陆 键，陆林军.基于RFID技术和FOAGRNN理论的高速公路道路关闭交通事件对车辆影响的判断模型［J］.武汉理工大学学报，2012，34（3）：63-68.

［12］ 郑朝辉，张 焱，裘聿皇.一种基于复数编码的遗传算法［J］.控制理论与应用，2003，20（1）：97-100.

［13］ 潘文超.应用果蝇优化算法优化广义回归神经网络进行企业经营绩效评估［J］.太原理工大学学报：社会科学版，2011，29（4）：1-5.

编辑顾逸斐

A Fruit Fly Optimization Algorithm Based on Com p lex Encoding

LU Mindi1，ZHOU Yongquan2，HUANG Kang1
（1.School of Computer and Electronics Information，Guangxi University，Nanning 530004，China；2.College of Information Science and Engineering，Guangxi University for Nationalities，Nanning 530004，China）

In view of the problems of easily relapsing into local extremum and low convergence precision of Fruit fly Optimization Algorithm（FOA），a fruit Complex Fly Optimization Algorithm（CFOA）encoding is proposed.It introduces the idea of complex encoding diploid，and the independent variables of the objective function are determined by the modules and angles of their corresponding comp lex numbers.Nine benchmark test functions are tested and comparative experimental results show that，compared with fruit fly optimization algorithm based on real encoding，fruit fly optimization algorithm based on complex encoding expands the quantity of information of individual genes and increases the diversity of population.

Fruit fly Optimization Algorithm（FOA）；diploid；real encoding；complex encoding

陆民迪，周永权，黄 慷.一种基于复数编码的果蝇优化算法［J］.计算机工程，2015，41（10）：181-185.

英文引用格式：Lu Mindi，Zhou Yongquan，Huang Kang.A Fruit Fly Optimization Algorithm Based on Comp lex Encoding［J］.Computer Engineering，2015，41（10）：181-185.

1000-3428（2015）10-0181-05

A

TP183

国家自然科学基金资助项目（61165015）；广西自然科学基金资助重点项目（2012GXNSFDA053028）；广西高校重大科研基金资助项目（20121ZD008，201203YB072）。

陆民迪（1989-），男，硕士，主研方向：智能计算；周永权，教授、博士；黄 慷，硕士。

2014-09-23

2014-11-06E-m ail：409658329@qq.com