基于统计特征向量的时序符号化改进算法

李晓翠，张新玉，罗庆云，任长安

（湖南工学院计算机与信息科学学院，湖南 衡阳421002）

基于统计特征向量的时序符号化改进算法

李晓翠，张新玉，罗庆云，任长安

（湖南工学院计算机与信息科学学院，湖南 衡阳421002）

传统基于统计特征向量的时间序列符号化算法不能较好地保留时序数据的特征信息，且不支持多维时间序列的符号化。为此，提出一种改进算法。对于单维时间序列，引入特殊点时间序列分割方法，在其基础上实施符号化。对于多维时间序列，在利用基于加权属性的主成分分析方法将多维时间序列转化为单维时间序列后，再实施符号化。实验结果表明，与传统算法相比，改进算法具有较高的精确度，且能保留时序特征点，同时支持多维时间序列的符号化。

多维时间序列；特征向量；加权属性；符号化；主成分分析

DO I：10.3969/j.issn.1000-3428.2015.10.029

1 概述

时序关联规则是数据挖掘领域中的研究热点［1］，而时序符号化则是时序关联规则挖掘的前提［2-3］。时序符号化一方面能够压缩时序，大幅减少时序关联规则挖掘的时间，另一方面能够使挖掘的时序关联规则更加精确。但由于时序数据的密集性、随机波动性及数据海量性，使得时序关联规则挖掘还存在诸多问题和难关，尤其在多维时序的关联规则挖掘方面更是如此。2003年，由Keogh等人提出了SAX符号化方法（Symbolic Aggregate Approximation）［4］，使得符号化方法进入了一个新的阶段，然而SAX仅用平均值来表示近似表示时序，使得符号化的结果不够精确。文献［5］提出了基于统计特征的时序数据符号化算法（SFVS），该算法将时序符号看作矢量，而各时序子段的均值和方差则分别作为描述其平均值及发散的程度。然而该算法中同样运用PAA方法（Piece-wise Aggregate Approximation）对时

序进行等宽分割，这样也就同样存在PAA分割方法的缺点：不能较好地保留时序的变化趋势及形态，且不支持多维时序的符号化。

本文针对单维时序和多维时序，分别引入特殊点的时序分割方法和加权属性的主成分方法，基于统计特征向量提出一种改进的时序符号化算法（ISFVS）。

2 基于统计特征特征向量的时序符号化算法

传统基于统计特征特征向量的时序符号化算法具体过程如下：

（1）时序规格化。

时序规格化计算公式如下：

其中，yi为时序的原始值；χi为规则化后的新值；μ和 σ分别为原始时序的期望值和方差［6］。

（2）PAA分段线性表示，并求出个时序字段的平均值和方差。

用wi，si分别表示第i个子序列上的平均值和方差，则：

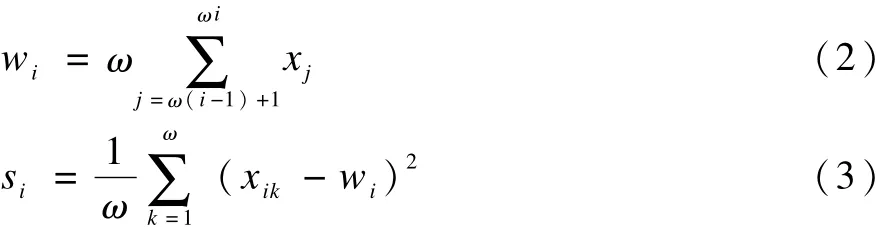
其中，ω为最大压缩比，ω一般采用如下经验公式：

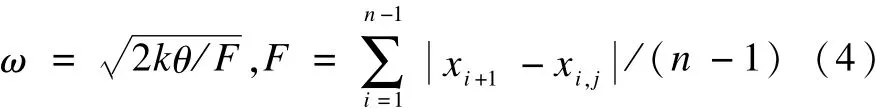
（3）根据符号集大小确定分裂点。

经过规格化的时序服从标准正态分布，因此，可以查表得到各等概率划分的分裂点，符号集与分裂点的关系如表1所示。

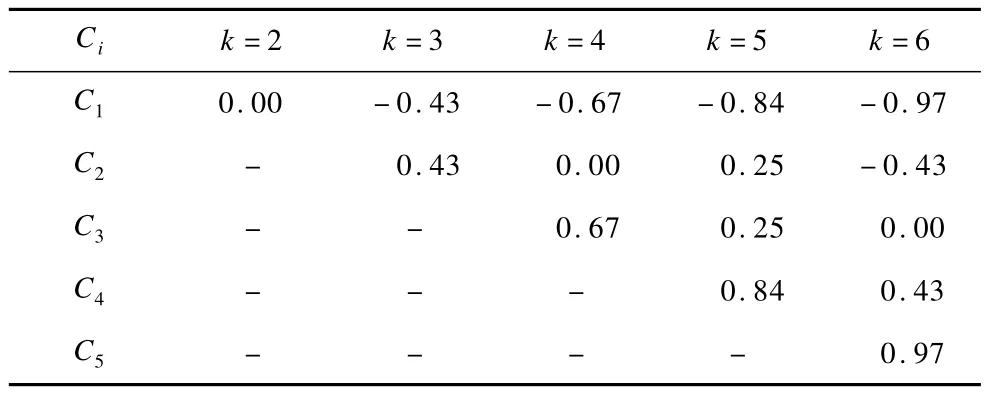
表1 k取不同值时所对应的划分点

（4）时序符号化的实施。

若用Ai来表示字符集A中的第i个字符。符号化准则为：将所有小于 C1的预处理数据用符号 A1表示，将大于C1且小于C2的预处理数据用符号A2表示，而将所有大于Ck-1的预处理数据用符号Ak表示。用向量Xi表示第Cs（SX，2）个子序列的符号结果。 则：

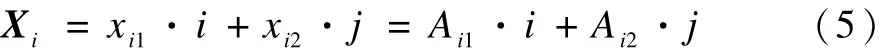
3 单维时序符号化

统计特征向量符号化［5］在对时序符号化时，针对SAX方法的缺陷，引入了方差这一因素，能够较好地描述时序特征，然而该方法中同样运用PAA方法对时序等宽分割，这样也就同样继承了PAA分割方法的缺点，不能较好地保留时序的变化趋势及形态，进一步影响时序关联规则挖掘的可信度。基于这个缺陷，结合时序分割方法，ISFVS方法引入了基于分段点的时序分割方法［6-7］，先对时序进行分割，然后用基于统计特征向量符号化的方法对时序实施符号化。

3.1 时序的分割

时序的分割是将时序数据表示成多段首尾相邻的近似直线，能够对时序进行有效压缩［8-9］，如图 1所示。

图1 时序分段线性化示意图

时序分段线性表示记为：将长度为 L的时序的n段时序，分段线性模型表示为S，如式（6）所示：

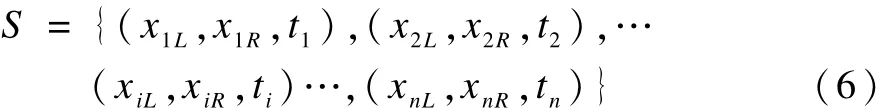
其中，i=1，2，…，n；χiL表示第i段的起始点的数值；χiR表示第i段结束点的数值；ti表示第i段的结束时间；n表示整个时序划分的直线段数目，tn=L。

3.2 符号化算法

单维时序符号化算法的具体步骤如下：

（1）时序规格化。

对时序实施符号化是基于标准正态分布的等概率规则来划分的。为了消除不同偏移量和振幅对符号化后相似性的影响，在对时序符号化之前必须先对其进行规则化处理，使时序满足平均值为0，方差为1的高斯分布。这一步骤和统计特征向量符号化方法是一致的。

定义1 将规则化后的时序记为 X=｛χ1（ν1，t1），χ1（ν2，t2），…，χn（νn，tn）｝。

（2）时序的分段点。

将规则化后的时序 X=｛χ1（ν1，t1），χ1（ν2，t2），…χn（νn，tn）｝，用基于特殊点的线段化方法求出规则化时序的所有分段点。

定义2 如果时序X上的某点满足如下条件之一：（1）νi＞νi-1且 νi≥νi+1，νi≥νi-1且 νi＞νi+1，其中1＜i＜n，则称 χi（νi，ti）为 X的正极值点；（2）νi＜

νi-1且νi≤νi+1，νi≤νi-1且νi＜νi+1，其中1＜i＜n，则称χi（νi，ti）为X的负极值点，称 χi（νi，ti）为局部极值点，即转折点。

定义3 定义时序X上的所有转折点为 S=｛S1，S2，…，Sn｝。

定义4 如果保持转折点Si的时间段与该序列的总长度的比值大于给定的阈值 C，则转折点Si为该时序的分段点。正转折点形成的分割点为正分割点，负转折点处形成的分割点为负分割点［10］。

由中心极限定理，可得 Δti满足 N［μ，σ2］的正态分布，其中n为局部极值点S集中元素的个数。

给定时序的最大压缩率［11］为 P，则被保留的分割点的总数占时序长度总个数的比例应不大于（1-P），即分割点的存在概率应小于或等于（1-P）。因此，被保留的分割点的Δti应分布在［u-χσ，u+χσ］的范围内（σ代表偏离 u的程度），概率小于或等于（1-P），令Y表示该随机事件，则有：

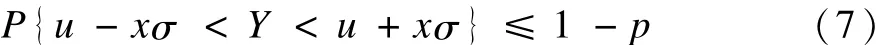
即2Φ（χ）-1≤1-P。

例如，要得到大于 90%的数据压缩率，则由式（9）得：

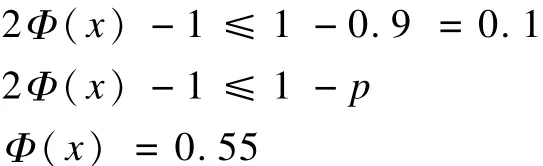
查表得χ=0.13，即若极值点χi为分段点，则该点的应用分布在［u-0.13σ，u+0.13σ］范围内。

根据以上算法，从局部极值点集合中，选择符合要求的分段点。

定义5 定义时间 D（S′1，S′2）≤D（S′1，S′3）+ D（S′3，S′2）上的所有分段点的所在位置集合为P=｛P1，P2，…，Pk｝。

（3）计算出各时序子段的均值和方差。

假设时序的起点位置为P0，终点位置为Pk+1，将其并入分段点位置集合 P，则 P=｛P0，P1，…，Pk，Pk+1｝，根据分段点集合P，可以将时序分割成k个子序列。用wi和si分别表示第i个子序列的平均值和方差，则第i个子序列的平均值为：

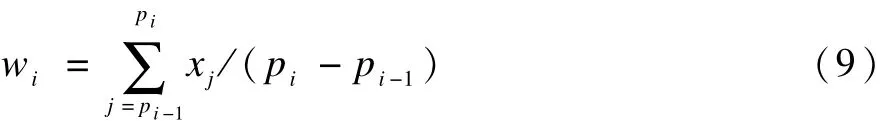
第i个子序列的方差为：

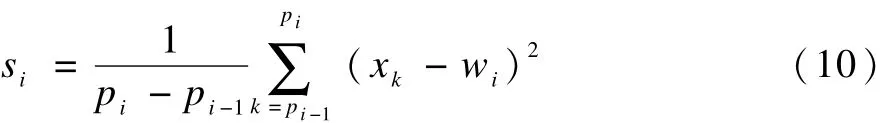
对时序预处理后，就可以根据字符集规模k（取3～20）和数据分布得到各个字符所代表数据区域的划分点。因此，划分点可以表示为：C=｛C1，C2，…，Ck-1｝。而划分点C是通过将整个正态分布区间划分成k个等概率区间的方式来确定，符号集规模 k和划分点的关系如表1所示。

（4）时序符号化的实施。

根据预处理结果及划分点集，将时序实施符号化。若用Ai来表示字符集A中的第i个字符。符号化准则为：将所有小于 C1的预处理数据用符号 A1表示，将大于C1且小于C2的预处理数据用符号A2表示，而将所有大于Ck-1的预处理数据用符号Ak表示。用Xi表示第 Cs（SX，2）个子序列的符号结果。 则：

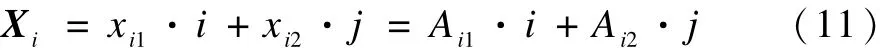
其中，Ai1表示第i个子序列的平均值wi所在区间的符号；Ai2表示第 i个子序列的方差 si所在区间的符号。

4 多维时序符号化

目前，主流的时序符号化方法只能解决单维时序的符号化问题或者对多维时序的符号化效果不佳。然而多维时序却普遍存在于各个领域，例如股票交易数据、移动通讯数据、气象数据等，多维时序的数据挖掘及关联规则的获取也必须建立在多维时序的相似性度量上。基于此，结合主成分分析法的思想，利用基于加权属性［12］的主成分法将多维时序转化成单维时序，然后按照单维时序的符号化方法对时序符号化。

4.1 基于加权属性的主成分方法

定义6 定义多维时序［13］为：

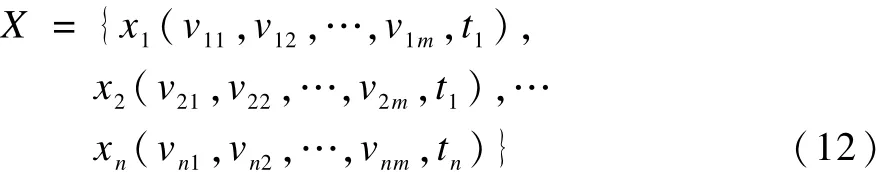
其中，m为多维时序的维数。

利用主成分分析法，求出原变量协方差矩阵的特征值 λi，并将它们从大到小排列，依次为 λ1，λ2，…，λm，相应的特征化标准向量为 γ1，γ2，…，γm，将所得的m个主成分按由大到小的顺序排列［14］，记为向量Y=（Y1，Y2，…，Ym），则主成分与原始变量之间存在如下关系：

通过以上方法将多维时序简化成单维时序。基于加权属性的主成分方法摒弃了直接选取个别主成分进行降维而造成的信息丢失的弊端，同时也避免了不降维而带来的算法复杂度高的缺陷。

4.2 符号化算法

多维时序符号化算法的具体步骤如下：

（1）用4.1节中基于加权属性的主成分方法将多维时序转化为单维时序；

（2）根据式（1）将上一步得到的单维时序规范化，使时序服从标准正态分布；

（3）用3.2节定义4中描述的方法，确定时序的分段点集合；

（4）由分段点集合，根据式（10）和式（11）计算出各时序子段的均值和方差；

（5）根据预设的符号集C，查表1确定各分裂点取值，从而实施对多维时序的符号化，将多维时序转化为符号化序列。

步骤（2）～步骤（5）的具体方法与统计特征特征向量符号化方法保持一致，这里不再具体阐述。

5 实验与结果分析

本文实验的运行环境为Interl©Celeron©CPU E3300@2.50 GHz，2.50 GHz，2 GB内存，500 GB硬盘，操作系统为32位W in 7，开发工具为Matlab 6.0及VS 2008，开发语言为C++及C#。为了验证改进统计特征符号化算法的优越性，及在多维时序中的可扩展性，采用了 2组数据进行实验分析。第1组数据来源于Time Series Data Library，http：// www.robhyndman.info/TS-DL。第2组数据为开滦集团某矿的提升机运行数据。其中，第1组数据均为单维时序数据，第2组为多维时序数据（提升机运行曲线包括给定速度、包络速度、实际速度、给定电压、电流）。

实验1 考察ISFVS算法是否能较好地保留时序特征点且具有较高的鲁棒性。

图2是原始序列图，图3是经过加入噪音数据后的序列图，图4则是加入噪音数据前后的时序分段点图。从图4可以看出加噪后的时序分割点与原始时序的分割点变化不大，绝大多数的分割点为时序特征点且位置保持不变，这是因为算法预处理阶段对时序进行了规范化处理，并且在选择分段点时，根据中心极限定理很好的去除了局部波动点，即实验中的噪声数据，因此，本文通过实验证明了改进ISFVS算法具有能保留时序特征信息且鲁棒性强的优点。

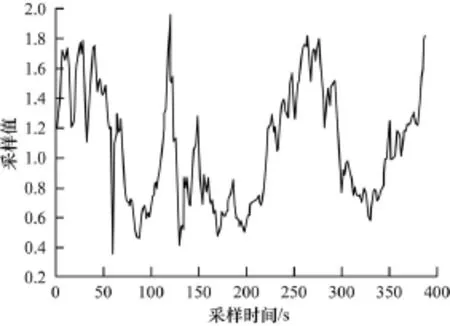
图2 原始时序图

图3 加噪序列图

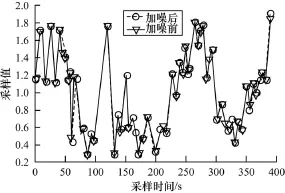
图4 分段结果

实验2 考察ISFVS算法对单维时序符号化优越性。为验证ISFVS算法对单维时序符号化表示的优越性，采用第1组实验数据，并将ISFVS算法同SFVS算法进行比较。

图5为ISFVS和SFVS符号化算法拟合误差结果比较。从图5可以看出，随着符号集的增大，SFVS和ISFVS算法的拟合误差逐渐减小，使得符号化后的序列逐渐接近于原始时序。同时，从图5还可以看出

ISFVS算法比SFVS算法更快的接近于原始序列，这是由于SFVS算法在对时序分割时，采用等分的原则，没有较好地保留时序形态模式，而ISFVS算法在对时序进行分割时，引入了特殊点的时序分割算法，该分割算法能够较好地保留时序的形态，使得符号化后的时序能够更加精确地表示原始时序。

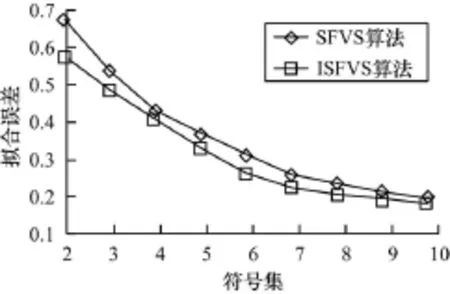
图5 单维时序拟合误差比较

实验3 考察ISFVS算法中提出的基于加权属性主成分算法的多维时序符号化算法的优越性。实验数据为第2组数据。为了验证ISFVS算法的优越性，同基于主成分算法多维时序符号化算法进行比较（选取第一主成分将多维时序转化为单维时序）。主成分算法的符号化算法简记为PCAS。图6给出了ISFVS和PCAS的执行时间；图7给出了ISFVS和PCAS在相同情况下的拟合误差。

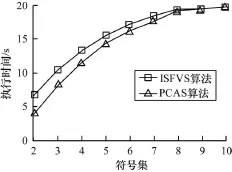
图6 执行时间比较

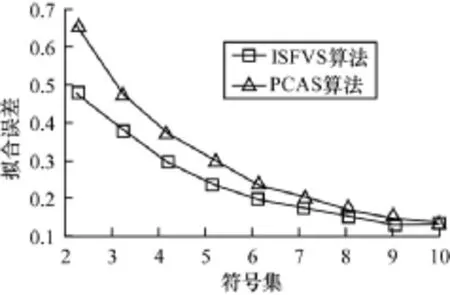
图7 多维时序拟合误差比较

从图6和图7可以看出，2种算法的执行时间即算法的运行效率是差不多的，然而基于加权属性的主成分的多维时序符号化算法在近似表示原始序列的能力上相对于PCAS有了较大的提升，由此可见ISFVS算法对多维时序符号化的优越性。

6 结束语

SFVS算法在SAX算法的基础上，增加了方差来描述时序，但没有解决必须等分时序的问题，且不能较好地保留时序形态特征。因此，本文将基于特殊点的时序分割算法引入到时序符号化算法中，结合统计特征向量提出了改进的符号化算法，同时利用主成分分析算法将其扩展到多维时序，设计基于加权属性的主成分多维时序符号化算法。实验结果表明，该算法在解决了必须等分时序问题的同时，也能够较好地保留时序形态特征，其在单维和多维时序符号化上均具有有效性及优越性。下一步将研究时序符号化算法在数据挖掘中的应用。

［1］ Butzer P L，Nessel R J.Fourier Analysis and Approximation［M］.［S.l.］：Academic Press，2011.

［2］ Chaovalit P，Gangopadhyay A，Karabatis G，et al.Discrete Wavelet Transform-based Time Series Analysis and Mining［J］.ACM Computing Surveys，2011，43（2）.

［3］ Fu T.A Review on Time Series Data Mining［J］. Engineering Applications of Artificial Intelligence，2011，24（1）：164-181.

［4］ Lin J，Keogh E，Lonardi S，et al.A Symbolic Representation of Time Series，with Implications for Streaming Algorithms［C］//Proceedings of the 8 th ACM SIGMOD Workshop on Research Issues in Data Mining and Know ledge Discovery.New York，USA：ACM Press，2003：2-11.

［5］ 钟清流，蔡自兴.基于统计特征的时序数据符号化算法［J］.计算机学报，2008，31（10）：1857-1864.

［6］ 闫秋艳，夏士雄.一种无限长时序的分段线性拟合算法［J］.电子学报，2010，38（2）：444-448.

［7］ 周大镯，李敏强.基于序列重要点的时间序列分割［J］.计算机工程，2008，34（23）：14-16.

［8］ 李重文，邓腾彬，马世龙.基于分段极值的时间序列数据查询显示方法［J］.计算机工程，2014，40（9）：27-30.

［9］ 李爱国，覃 征.在线分割时序数据［J］.软件学报，2004，15（11）：1671-1678.

［10］ 肖 辉，马海兵，龚 薇.基于时态边缘算子的时间序列分段线性表示［J］.计算机工程与应用，2008，44（19）：156-159.

［11］ 詹艳艳，徐荣聪，陈晓云.基于斜率提取边缘点的时间序列分段线性表示方法［J］.计算机科学，2006，33（11）：139-142.

［12］ 杜 奕，卢德唐，李道伦，等.基于层次聚类的时间序列在线划分算法［J］.模式识别与人工智能，2007，20（3）：23-27.

［13］ Keogh E，Chakrabarti K，Pazzani M J，et al.Dimensionality Reduction for Fast Similarity Search in Large Tim e Series Databases［J］.Know ledge and Information System s，2008，3（3）：263-286.

［14］ Yi B K，Faloustsos C.Fast Time Sequence Indexing for Arbitrary Lp Norm s［C］//Proceedings of the 26th International Conference on Very Large Databases. Cairo，Egypt：［s.n.］，2000：385-394.

编辑 金胡考

Improved Symbolic Algorithm of Time Series Based on Statistical Feature Vector

LI Xiaocui，ZHANG Xinyu，LUO Qingyun，REN Chang’an

（School of Computer and Information Science，Hunan Institute of Technology，Hengyang 421002，China）

The traditional symbolic algorithm of time series based on statistical feature vector can not retain the timing characteristics well and support multidimensional time series symbolic.Aiming at this problem，this paper proposes an improved symbolic algorithm of time series based on statistical feature vector.The specific methods are as follow s：for single-dimensional time series，using special points’time series segmentation method to segment the time series and making it symbolic；for multi-dimensional time series，using weighted attributes’Principal Component Analysis（PCA）method to transform the multi-dimensional time series into single time series，then making it symbolic.Experimental result show s that the improved algorithm has higher accuracy than traditional algorithm.It can retain the timing characteristics and has more superiority in the aspect of multidimensional time series symbolization.

multidimensional time series；feature vector；weighted attribute；symbolic；Principal Component Analysis（PCA）

李晓翠，张新玉，罗庆云，等.基于统计特征向量的时序符号化改进算法［J］.计算机工程，2015，41（10）：155-159.

英文引用格式：Li Xiaocui，Zhang Xinyu，Luo Qingyun，et al.Improved Symbolic Algorithm of Time Series Based on Statistical Feature Vector［J］.Computer Engineering，2015，41（10）：155-159.

1000-3428（2015）10-0155-05

A

TP18

湖南省教育厅科学研究基金资助项目（14C0304）；国家自然科学基金资助项目（61402164）；湖南省科技计划基金资助项目（S2013F1023）。

李晓翠（1986-），女，硕士研究生，主研方向：数据挖掘；张新玉，硕士研究生；罗庆云，教授；任长安，讲师。

2014-10-10

2014-11-14E-mail：xiaocuiworld@163.com