基于ABAQUS/CFD的径向滑动轴承数值模拟

徐　欣

上海电气集团股份有限公司 中央研究院　上海　200070



基于ABAQUS/CFD的径向滑动轴承数值模拟

徐欣

上海电气集团股份有限公司 中央研究院上海200070

摘要：针对滑动轴承润滑机理复杂，编程研究困难的问题，采用ABAQUS/CFD软件建立了径向滑动轴承计算流体动力学仿真模型，分析得到了稳态下油膜压力、油膜温度与油膜流速的分布规律，为滑动轴承的设计、制造和试验提供了理论依据，也为后续可倾瓦滑动轴承的数值模拟提供有益参考。

关键词：径向滑动轴承； 计算流体动力学； 数值模拟

Abstract：Aiming at the complexity in bearing lubrication mechanism and difficulties in programming for examination, ABAQUS / CFD software was adopted to establish a simulation model to calculate fluid dynamics of radial sliding bearing and by analyses it was available to obtain regularities of distribution involving the oil layer pressure, oil layer temperature and velocity of oil layer flow providing a theoretical basis in design, manufacture and test of sliding bearings, and providing a useful reference for subsequent numerical simulation of the tilting pad journal bearings.

Key Words：Radial Sliding Bearing； Computational Fluid Dynamics； Numerical Simulation

旋转类装备机械正朝着高速、重载和高精密方向发展，作为其核心部件的滑动轴承在此过程中扮演着重要角色，因此对其提出了更高的要求[1,2]。目前国内外学者在工程应用上仍通过有限差分等方式来求解雷诺方程，借助人工编程，进而计算滑动轴承的静动特性[3,4]。而雷诺方程是N-S方程(纳维-斯托克斯方程)的简化，推导过程忽略了假设黏度、惯性项和密度不变等因素的影响[5]，对于结构复杂的轴承，编程工作更是费时费力，传递性也不够好。

CFD(计算流体动力学)是流体力学与计算机的结合，可通过数值模拟和图像显示对流体润滑进行仿真分析，用一系列离散单元来模拟原本在时间和空间域上连续的物理场，通过建立这些单元上场变量的代数方程组并加以求解，从而得到场变量的近似值，最终获得整体流场的数值解。近年来，Fluent、CFX等CFD软件应运而生，在工程应用方面取得了不错的效果。涂林[6]利用计算流体动力学软件Fluent分析了动压滑动轴承油膜的稳定性，给出了防止油膜振荡的措施。孟凡明[7]等人探讨了CFX和Fluent软件在径向滑动轴承润滑计算中的异同。Dimitrios[8]等人则同时使用CFD和FEA(有限元分析)对磁流变液轴颈轴承进行了多物理场耦合的仿真分析。但是上述软件也存在网格划分需要其它软件预处理、数据传输存在失真等弊端，ABAQUS/CFD是ABAQUS6.10后出现的专门用于流体分析的模块，它采用混合有限体积法和有限元法的方式来计算不可压缩流体的层流和湍流问题，可在一个统一的环境中完成流体分析的前、后处理，便于实现参数化建模与分析，运算效率高。

本文基于ABAQUS/CFD，建立了某滑动轴承试验台用径向滑动轴承的油膜模型，完成了六面体网格划分和边界条件的设置，计算并分析了稳态下径向滑动轴承的油膜压力、油膜温度及油膜流速等分布规律，为物理试验台的建设和进一步的试验研究提供了理论依据和仿真参考。

1控制方程

流体运动遵循的物理定律主要包括质量守恒定律(连续性方程)、动量守恒定律(运动方程)和能量守恒定律。本文涉及的宏观流体力学范围内的流体运动，可由以下控制方程进行描述。

1.1　连续性方程

单位时间内，流入某流体微元的质量与流出的质量之差等于该流体微元质量的增量，即：

(1)

当流体不可压且定常流动时，式(1)可写成：

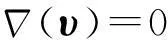
(2)

1.2　动量守恒方程

流体微元中动量对时间的变化率等于流体微元所受外部作用力之和，即：

(3)

式中： p为流体微元上的压力；τ为应力张量；F为外部的体积力；g为重力加速度。

由于滑动轴承内部流场黏性力远大于惯性力，并且无其它外力源，因此可以得到稳态求解的动量方程：

(4)

(5)

式中： μ为黏性系数；I为单位张量。

1.3能量守恒方程

流体微元中输入与输出的能量之差等于总能量的增量，即：

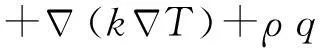
(6)

2模型的建立

2.1　几何模型

以径向圆柱滑动轴承为研究对象，轴承结构尺寸为： 直径D=150mm，轴承宽度B=90mm，进油口直径din=18mm，出油口直径dout=15mm，半径间隙c=0.04mm，如图1所示。润滑油从上部进油口进入楔形油腔，在转子旋转带动其运动过程中先流经出油口，再从两端面引出。采用三维建模软件SolidWorks建立轴承与转子间的三维油膜几何模型，然后以.stp格式导入ABAQUS软件进行边界条件的设置及网格划分，如图2所示。

图1　滑动轴承结构示意图

图2　油膜模型

2.2　基本假设与边界条件

边界条件： 润滑油密度ρ=860kg/m3，润滑油动力黏度μ=0.0277Pa·s，进油压力取pin=1MPa，初始平均油温20℃，环境温度为18℃，出油背压pout=0.101MPa，与大气压相等，润滑后油温上升，转子旋转速度为1000r/min，其余均为固壁边界。

2.3　网格划分

滑动轴承油膜厚度方向尺寸相比模型半径和宽度尺寸非常小，而厚度方向却是计算的关键方向，必须划分足够的网格层数以保证壁面速度梯度不影响流场结果，因此整体油膜网格数必将达到很大的数目，并且可能会形成狭长的网格单元，容易引起计算不收敛现象，所以需要进行六面体网格划分。理论上，网格数越多，计算精度越高，但计算耗时越长，对计算机性能的要求也越高。为了寻找到一个合适的网格密度，确定网格独立性，以便今后对该类模型进行大量计算，形成统一数据库，本文以某节点油膜压力和油膜温度为计算指标，通过对8组不同网格密度模型的反复试算，得到了网格独立性曲线，如图3所示。由图3可知，随着网格数的增多，压力和温度值有所下降，但幅度越来越小，到120万网格时已满足前后误差为1%的设计精度；相反，计算耗时却由5min延长至大约180min。综合考虑以上因素，本文最终选取六面体网格总数为120万的计算模型，网格划分结果如图4所示。

图3　网格独立性曲线

图4　油膜网格划分

3结果与分析

设置好边界条件及完成网格划分后，就可以直接在ABAQUS/CFD中生成.inp文件提交计算。需要指出的是，本文所进行的径向滑动轴承CFD仿真分析是为下一步四瓦可倾瓦径向滑动轴承的CFD仿真分析提供参考，因此在油膜结构形式及进、出油口边界的设置上与可倾瓦轴承相似，只是还未设置瓦块随润滑油流动而偏摆等边界条件。

ABAQUS/CFD不仅可以在一个环境中进行模型的前、后处理，而且可以同时进行流场、温度场等多物理场耦合分析。本文的模型边界条件设置如2.2节所述，既定义了流速、压强等动量方程参数，同时又定义了油温、环境温度等热能方程参数，计算结果如图5~图7所示。

图5　油膜压力分布

图6　油膜温度分布

图7　油膜流速分布

由图5可知，最大油膜压力0.1043MPa，出现在轴承下方靠近本文所设置的偏位角附近。由于起承载作用的主要是轴承下半圆，因此下半周油膜平均压力大于上半周油膜平均压力，这是由于转子带动油膜顺时针转动并伴有一定偏位造成的。以油膜压力最大位置为界，向两边逐渐减小，最小油膜压力位置出现在轴承顶部进油口右侧附近，这种油膜压力分布趋势可为滑动轴承物理试验台中压力传感器的安装提供理论依据。

图6(a)为油膜温度分布图，图6(b)为图6(a)的局部放大图，便于观察油膜厚度方向的温度分布。本文设置环境温度为18℃，进口油温为20℃，可以发现，转子带动润滑油流动使油温上升，最高油温为25℃，整体沿偏位线呈近似对称分布。膜厚较小的左下方承载区由于摩擦剧烈，油温上升显著。顺时针转速的影响，加之出油口的存在易于散热，使其附近油温相对较低，并在周向存在逐级递减趋势。结合图6(b)局部放大图可以发现，在油膜厚度方向上，油温内侧高于外侧，这是转子带动油膜高速旋转导致内侧油速大于外侧油速所致。油膜温度分布图可为物理试验中温度传感器的布置提供理论依据。

图7(a)为油膜流速分布图，图7(b)为图7(a)的剖面局部放大图，便于观察油膜厚度方向的流速分布。本文设油膜外侧为壁面，转速为零，内侧随转子无滑移地转动，因此最大流速为7850mm/s，流速由内而外逐级递减。结合图7(b)局部放大图可以发现，在出口位置，流体流速也是由内而外逐级递减，并在出油口一侧平稳流出润滑油，出口拐角位置未出现较大扰动，表明滑动轴承的润滑油出口形状及其尺寸的设计比较合理。

4结论

采用ABAQUS/CFD软件建立了径向滑动轴承CFD计算模型，完成了六面体网格划分及网格独立性分析，确定了合适的模型边界条件，得到了滑动轴承油膜压力、油膜温度及油膜流速的分布规律，解决了现实中因油膜极薄难以进行直接测量的问题。该方法为滑动轴承的设计、制造和试验提供了理论依据，能够缩短滑动轴承的研发周期，减少试验费用，同时也可为后续可倾瓦轴承的仿真与试验提供参考。

参考文献

[1] 种崴，崔敏，童水光.油膜润滑条件下滑动轴承变形和应力数值模拟[J].浙江大学学报,2012,46(7)： 1227-1232.

[2] 余四平.高速离心泵径向滑动轴承承载能力分析[D].南京： 南京林业大学，2012.

[3] 吕延军，虞烈，刘恒.非线性轴承-转子系统的稳定性和分岔[J].机械工程学报,2004,40(10)： 62-67.

[4] V Meruane，R Pascual. Identification of Nonlinear Dynamic Coefficients in Plain Journal Bearings [J]. Tribology International, 2008，41(8)： 743-754.

[5] 马涛，戴惠良，刘思仁.基于Fluent的液体动静压轴承数值模拟[J].东华大学学报,2010,36(3)： 279-282.

[6] 涂林.基于Fluent的动压滑动轴承油膜稳定性研究[D].太原： 太原理工大学，2011.

[7] 孟凡明，陈原培，杨涛.CFX和Fluent在径向滑动轴承润滑计算中的异同探讨[J].重庆大学学报,2013,36(1)： 7-14.

[8] Dimitrios A B，Pantelis G N. CFD Simulation of Magnetorheological Fluid Journal Bearings [J]. Simulation Modeling Practice and Theory, 2011，19(14)： 1035-1060.

中图分类号：TH133.2

文献标识码：A

文章编号：1674-540X(2015)02-048-05

作者简介：徐欣(1986-)，男，硕士，主要从事数字化设计研发工作，E-mail： xuxin3@shanghai-electric.com

收稿日期：2015年3月