降雨入渗条件下非饱和土质边坡的稳定性分析

徐 全， 谭晓慧， 辛志宇， 汪贤恩， 谢 妍

（合肥工业大学 资源与环境工程学院，安徽 合肥 230009）

土质边坡常处于非饱和状态，降雨对于非饱和状态的土质边坡稳定性具有重要影响。雨水在非饱和土质边坡中的渗流是一个典型的流固耦合过程。关于非饱和土的流固耦合，国内外学者做了很多相关研究。文献［1］提出了考虑非饱和土变形的热、气、水运动耦合理论；文献［2］进行了非饱和土的固结耦合数值计算；文献［3］进行了雨水入渗下非饱和土边坡渗流场和应力场耦合的数值模拟；文献［4］对降雨作用下土质边坡的流固耦合与非耦合分析进行了对比研究。

非饱和土质边坡稳定性的影响因素很多，其中包括力学参数、水力参数、降雨强度等等。文献［5］基于边坡土体参数变异性的前提下用响应面法分析了边坡的失效概率；文献［6］分析了饱和渗透系数及不同降雨模式对边坡稳定性的影响。文献［7］对降雨入渗情况下的土质边坡进行了水力学参数的敏感性分析；文献［8］分析了长时间小强度降雨对边坡稳定性的影响；文献［9］从降雨模式、非饱和土抗剪强度理论、土体含水量变化这3个方面研究了降雨对非饱和土质边坡的影响。

基于非饱和土的强度理论，非饱和土质边坡在降雨入渗的过程中，随着雨水的入渗，土体中的饱和度逐渐增大，基质吸力逐渐减小，从而导致非饱和土的抗剪强度减小，边坡的稳定性降低。国内外很多学者研究了基质吸力对非饱和土质边坡稳定性的影响［10－12］。此外，文献［13－14］还分析了浸润峰对非饱和土质边坡安全系数的影响。

降雨作用下影响非饱和土质边坡稳定性的因素很多，而且这些因素具有较大的不确定性。因此，本文首先在参数取均值的条件下探讨降雨模式对非饱和土质边坡的稳定性的影响，以浸润峰深度和基质吸力降低深度来表征各种情况下渗透的特征，分析各因素对基质吸力降低深度、边坡安全系数及滑面位置影响；再分析参数的变异性对非饱和土质边坡稳定性的影响，研究边坡的稳定性与相应参数变化趋势之间的关系。

1 理论基础

1.1 理论基础

假设土体中的空隙完全被液相流体（w）及气相流体（g）填充，则液相的饱和度Sw和气相的饱和度Sg满足（1）式，即

且它们分别满足传导定律、流动平衡定律和流体本构定律。

液相、气相的传导定律分别为：

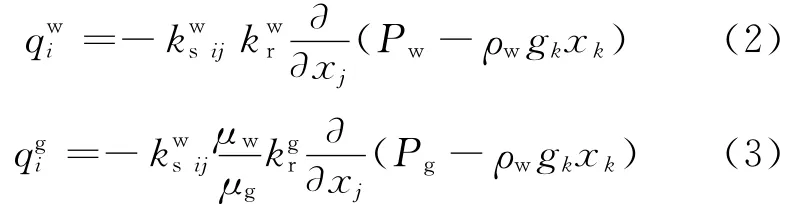
液相、气相的流动平衡定律分别为：

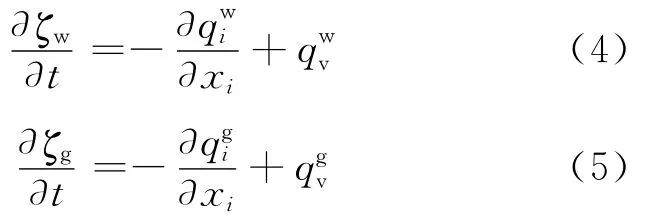
液相、气相的流体本构定律分别为：

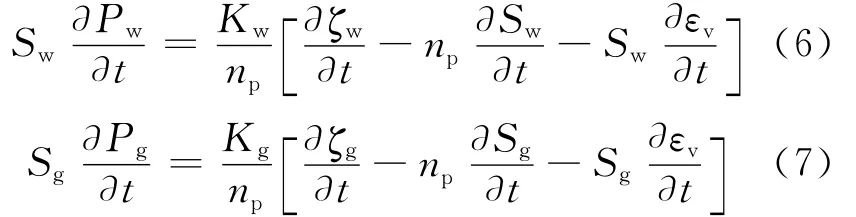
其中，上、下标w、g分别代表液相及气相；ζ为流体容量的变化；t为时间；q、μ、P、ρ、g及K分别为流体的渗流速度、动力黏滞度、压力、密度、重力加速度及体积模量；np及εv分别为土体的孔隙度及体积应变；ks、kr分别为饱和及相对渗透系数，渗透系数k的单位是m2·Pa／s，它与用水头表示的渗透系数Ks（单位为cm／s）的关系［15］是：k＝Ks×1.02×10－6。

当进行流固耦合计算时，有效应力的变化会产生体积应变；同时，体积变形又反过来造成流体压力的变化。因此，为考虑固相和液相及气相之间的耦合作用，需要引入固相的平衡方程、本构方程及几何方程。

平衡方程：

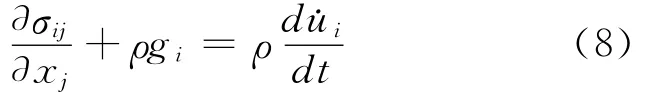
本构方程：

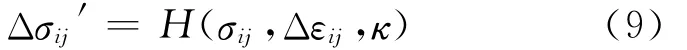
几何方程：

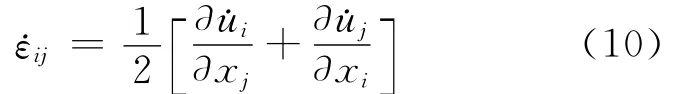
其中，σ为总应力；σ′为有效应力；˙u为速度；κ为历史参数；H为本构定律的函数形式；Δ表示变量增量。本文设土体是理想弹塑性模型，其屈服条件满足摩尔 －库仑屈服准则［16－17］。

对于两相流问题，有效应力可以定义为

其中，δij为克罗内克尔符号。本文采用有限差分软件FLAC的两相流模块来进行饱和、非饱和渗流分析［14］。

1.2 非饱和土的土水特征及渗透系数

非饱和土的土水特征可以用土水特征曲线（SWCC）来描述，SWCC是表示基质吸力（以下简称吸力）与含水率或饱和度的关系曲线。在两相流中，吸力ψ是气相压力（Pg）与液相压力（Pw）的差值（ψ＝Pg－Pw），它是液相饱和度Sw的函数。当采用van Geneutchen－Mualem 模型［18］来描述SWCC时，其表达式如下：

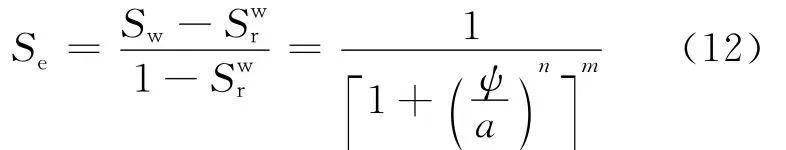
其中，m＝1－1／n；为液相的残余饱和度；a、n、m为拟合参数；Se为相对渗透系数。

流体的渗透系数可用饱和渗透系数与相对渗透系数的乘积来表示。根据van Geneutchen的相对渗透性经验公式，可以求得液相及气相的相对渗透系数分别为：

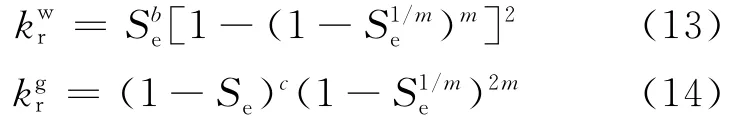
其中，b、c为拟合系数（一般取b＝c＝0.5）。

1.3 非饱和土的强度理论

非饱和土强度理论以Mohr－Coulumb准则为基础，目前有2类强度公式被岩土工程界广泛认可，分别为Bishop公式［19］及Fredlund的双应力变量公式［20］。其中，Bishop公式是用非饱和土的有效应力代替饱和土的有效应力而得到的，其表达式为：

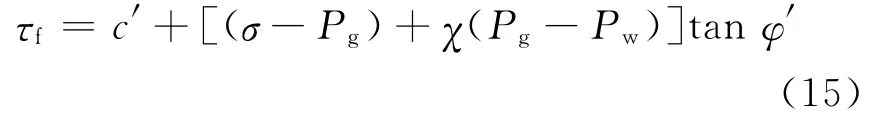
其中，τf、c′和φ′分别为土的抗剪强度、有效黏聚力和有效内摩擦角；σ、Pg、Pw分别为正应力、孔隙气压力和孔隙水压力；χ为有效应力系数，主要取决于饱和度。本文进行边坡稳定性分析时采用Bishop抗剪强度公式。

对于非饱和土质边坡，考虑降雨入渗时，先进行饱和、非饱和渗流分析，求得各单元及各结点的应力及应变分布；再采用强度折减法进行边坡的稳定性分析，求得边坡的安全系数及对应的临界滑动面的位置［21］。

2 算例分析

2.1 计算条件

某均质土坡高10m，坡角45°，初始水位面与水平面间的夹角为5°，其计算模型及网格划分如图1所示。图中粗实线为特定的研究剖面（距离坡脚处15m），用于讨论分析降雨过程中剖面上的饱和度及吸力降低深度的变化规律。

数值计算时，对模型的左、右边界约束水平位移，对底边界约束水平及竖直位移；设坡表为入渗边界，左、右边界为定水头边界，底边界为不透水边界。设初始水位面以上任一点的负孔隙水压力与该点距水位面的距离成正比，计算时考虑流固耦合作用。

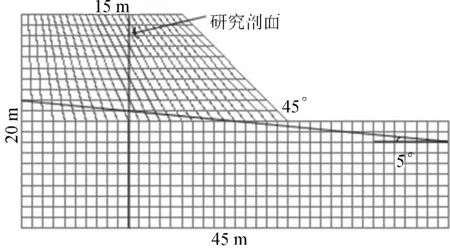
图1 边坡剖面图

降雨作用下，影响土质边坡稳定性的参数主要有强度参数及水力参数。其中，强度参数主要是土的黏聚力及内摩擦角；水力参数主要有SWCC拟合参数a、n及饱和渗透系数（为简化起见，下文分别以Sr及ks代表及ks

w）。这6个参数的均值及变异系数由室内试验求得，详见表1所列。为了分析土体渗透性大小对计算结果的影响，还考虑了饱和渗透系数为60mm／d的情况。计算时，分析了 A、B、C、D 4种降雨模式对土质边坡稳定性的影响，这4种降雨模式的降雨强度、持续时间及降雨量见表2所列，各种模式的总降雨量相同。降雨作用下边坡的稳定性是一个与时间有关的过程［3］，但本文的重点不是研究边坡的时变稳定性，因此只以降雨停止时刻为例进行结果分析。

表1 计算参数

表2 降雨模式

2.2 参数取均值时的边坡稳定性分析

2.2.1 降雨模式对土体饱和度的影响

通过饱和、非饱和渗流计算，可以求得边坡中各点的液相饱和度及气相饱和度，两者之和为1。以液相饱和度（以下简称饱和度）为例，它与深度的关系可用边坡中某一特定剖面上的饱和度－深度曲线来表示。饱和渗透系数ks1＝60mm／d和ks2＝6mm／d时，研究剖面上饱和度与深度及降雨模式关系如图2所示。

图中O为降雨前的状态，A、B、C、D分别代表4种降雨模式。

由图2可见，在降雨前，饱和度随着深度由坡表向下而单调增加；深度增至初始水位面时，饱和度增加至1，即土体完全饱和。但是，由于降雨入渗的影响，在距坡表的一定范围内，边坡中饱和度－深度曲线的形状在降雨后发生了明显的变化。随着深度由地表向下增加，饱和度先减小至某个极值，再沿着降雨前的曲线逐渐增加。各降雨模式下饱和度－深度曲线偏离降雨前相应曲线的点见图中空心三角形所示，该点距坡表的竖直距离即为湿润前锋的深度［14］Dw。

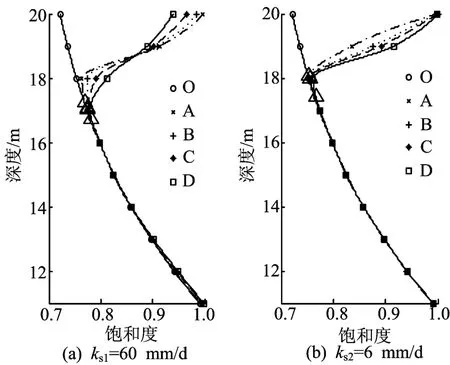
图2 饱和度与深度及降雨模式的关系

对比图2a、图2b可发现，降雨模式对边坡土体饱和度的影响与饱和渗透系数的大小有关。饱和渗透系数较大时，各降雨模式对应的饱和度－深度曲线相互交叉。而饱和渗透系数较小时，各降雨模式对应的饱和度－深度曲线则依次降低。具体而言，在渗透系数较大的情况下（图2a），对于短时间的强降雨（如降雨模式A），坡表处的饱和度相对较大，但其湿润前锋位置却较浅。这表明雨水在短时间内来不及充分入渗，主要集中在边坡的表层。而对于长时间的小强度降雨（如降雨模式D），坡表处的饱和度相对较小，但其湿润前锋位置却最深。这表明长时间的小强度降雨有利于雨水向土层更深处入渗。在渗透系数较小的情况下（图2b），各降雨模式对应的坡表土体饱和度近似相等；随着深度由坡表向下增加，降雨模式A、B、C、D对应的饱和度－深度曲线依次降低；它们对应的湿润前锋深度也逐渐增加，但各降雨模式的湿润前锋深度值相差不大。这表明当土体的饱和渗透系数较小时，雨水较难入渗至土体中，因此总降雨量一定时，各降雨模式对土体饱和度的影响无明显差别。

2.2.2 降雨模式对土体吸力的影响

ks1＝60mm／d及ks2＝6mm／d时，研究剖面上吸力与深度及降雨模式的关系如图3所示。由于饱和度与吸力有一一对应的关系（见（12）式），因此降雨模式对吸力的影响规律与图2中对饱和度的影响规律较为一致。

图2与图3的区别是：图2中，降雨前的饱和度－深度曲线是非线性的；而图3中，降雨前的吸力－深度曲线是线性的。

图2中饱和度－深度曲线的非线性是由土水特征曲线的非线性而引起的。

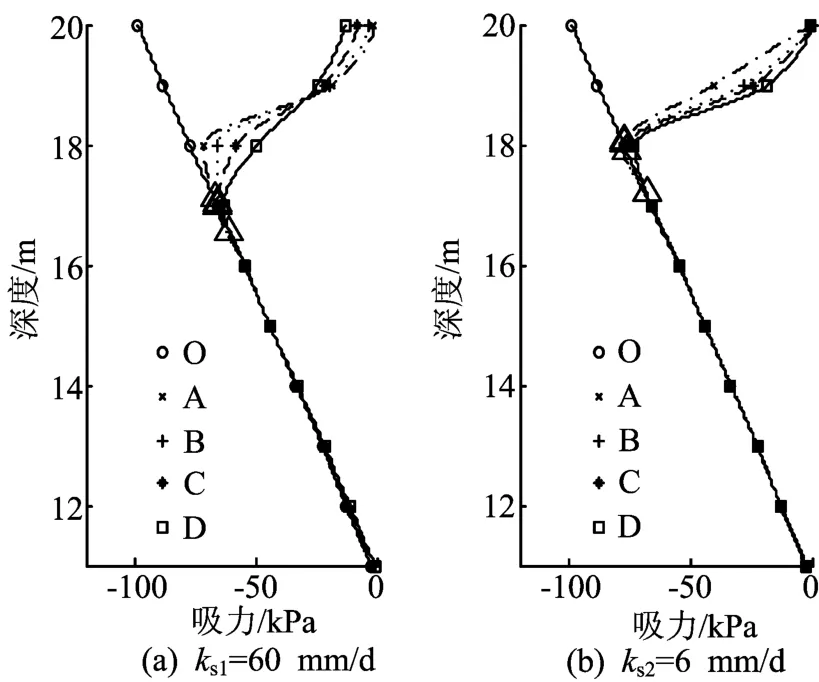
图3 吸力与深度及降雨模式的关系

由于吸力直接影响土体抗剪强度的大小，吸力的变化对边坡稳定性的影响更为直观。因此，与湿润前锋Dw的定义类似，可由图3定义吸力降低深度Ds，即各降雨模式下的吸力－深度曲线与降雨前吸力－深度曲线的交叉点至边坡表面的竖直距离。

2种饱和渗透系数下吸力降低深度Ds与降雨模式的关系如图4所示。

由图4可见，饱和渗透系数及总降雨量一定时，随着降雨强度的减小及降雨历时的增加，吸力降低深度也相应增加，其中，饱和渗透系数较小时，Ds随着降雨模式的变化更为明显。对于同一降雨模式，随着饱和渗透系数的增加，吸力降低深度也明显增加。

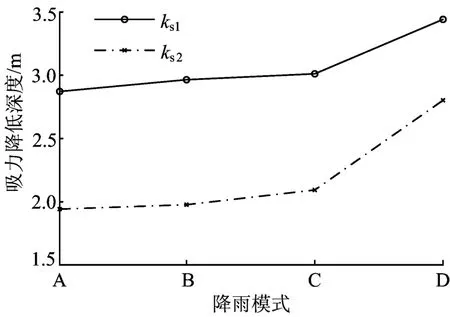
图4 吸力降低深度与降雨模式的关系

2.2.3 降雨模式对边坡安全系数的影响

2种饱和渗透系数条件下，边坡安全系数Fs与降雨模式的关系如图5所示。

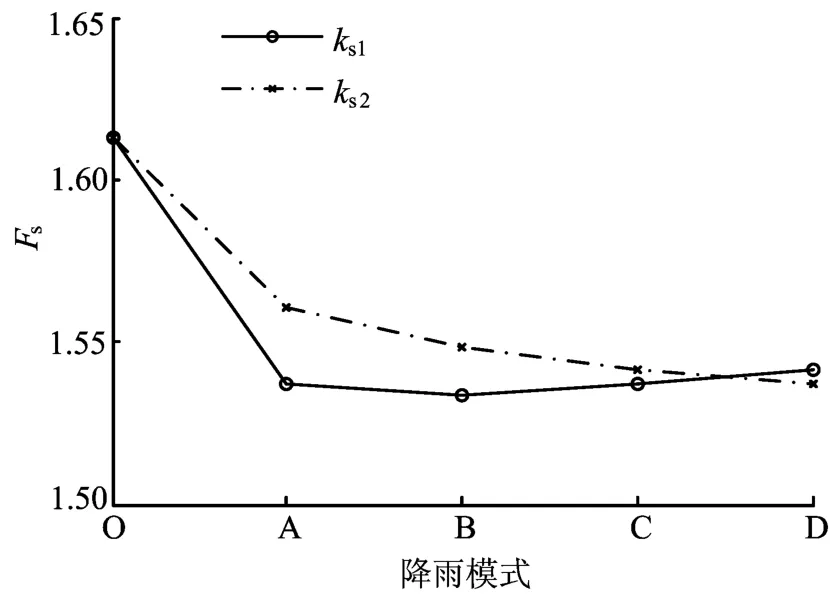
图5 安全系数与降雨模式的关系

由图5可见，各种降雨模式下，边坡的安全系数Fs与降雨前相比都明显降低。Fs的变化规律与饱和渗透系数的大小有关。饱和渗透系数越大，降雨后边坡的安全系数越低；当饱和渗透系数较大时，4种降雨模式对应的边坡安全系数几乎相同，即总降雨量一定时，不同降雨模式对边坡稳定性的影响较为一致；当饱和渗透系数较小时，边坡安全系数Fs随着降雨强度的减小及降雨历时的增加而逐渐降低。

产生这种现象的原因可以结合图4来解释。由图4可见，饱和渗透系数较大时的吸力降低深度明显大于饱和渗透系数较小时的吸力降低深度。而吸力降低深度Ds越大，在此深度范围内土体的抗剪强度就越小，此时边坡的安全系数Fs也就越小。因此，降雨模式相同时，饱和渗透系数越大，边坡的安全系数就越小。同时，饱和渗透系数较大时，由于吸力降低深度已足够大，雨水能充分入渗，因此各种降雨模式对应的边坡安全系数接近相同；而饱和渗透系数较小时，吸力降低深度相应较小，雨水还未能充分入渗到边坡土体中，此时，吸力降低深度越大，边坡的安全系数就越小。

2.2.4 降雨模式对边坡潜在滑面位置的影响

各种降雨模式下，边坡的潜在滑面位置分别如图6所示。

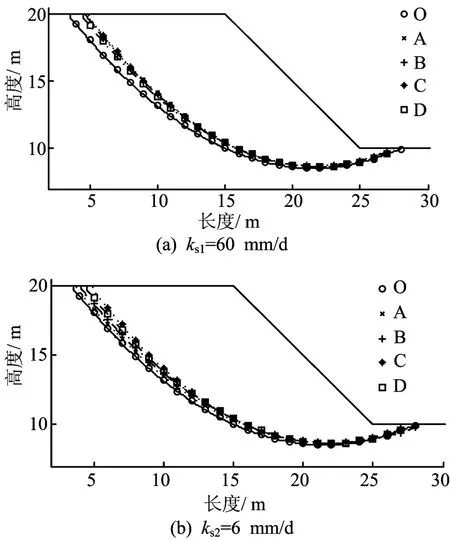
图6 边坡潜在滑面与降雨模式的关系

由图6可见，降雨会引起边坡潜在滑面位置向上移动，使滑面位置变浅。其中，坡顶处滑面位置变化较为明显，而坡底处的滑面位置则几乎不变。总降雨量相同时，对于较大的饱和渗透系数情况，雨水的入渗相对较为充分，因此各降雨模式对应的边坡滑面位置几乎相同。而对于较小的饱和渗透系数情况，雨水相对较难入渗到土体中，因此滑面位置与降雨强度有关。由图6b中边坡滑面位置的变化可以看出，滑面位置并不是随着降雨强度的减小及降雨历时的增加而一直变浅，而是在某种降雨模式下达到最浅（如降雨模式C）；之后，滑面位置会随着降雨强度的减小及降雨历时的增加而逐渐趋向于恢复最初状态，故滑面位置又略有降低（如降雨模式D）。对比图6a、图6b可见，2种饱和渗透系数对应的滑面位置变化范围较为一致。

2.3 参数变异性对边坡稳定性的影响

由于参数存在变异性，下面分析参数在其均值附近波动时，边坡中吸力、安全系数及滑面位置的变化规律，并进一步分析这些量对各种力学参数及水力参数的敏感性。由于饱和度与吸力存在对应关系，此处不再分析饱和度与深度及降雨模式的关系。

计算中，分别取各参数在其均值附近按1倍均方差的幅度进行波动。记基本变量X＝［c′φ′anSrks］，则对于任一分量Xi（i＝1，2，…，6），其上下限分别为Xi＋＝Xi＋σXi，Xi－＝Xi－σXi。其中，σXi＝μXiδXi为变量Xi的均方差，μXi及δXi分别为变量Xi的均值及变异系数，其数值见表1。

对于基本变量X＝［c′φ′anSrks］，变量数为6。分别取每个基本变量在其均值附近上下波动而其他变量仍取均值，共可得到12组数据；再加上1组均值数据，共有13组计算参数。

计算分析表明，不同饱和渗透系数及降雨模式下，各参数对饱和度、吸力、安全系数及滑面位置的影响规律较为一致，因此只以饱和渗透系数ks1＝60mm／d及降雨模式A为例进行分析。

2.3.1 参数变异性对土体吸力的影响

研究剖面上吸力－深度曲线与土体参数间的关系如图7所示。由于力学参数的改变对雨水的渗透及土体的吸力不产生影响，图中只绘出了水力参数（X3～X6）的变异性对吸力的影响。可见，在4个水力参数中，各参数的变异性对土体吸力都产生影响。

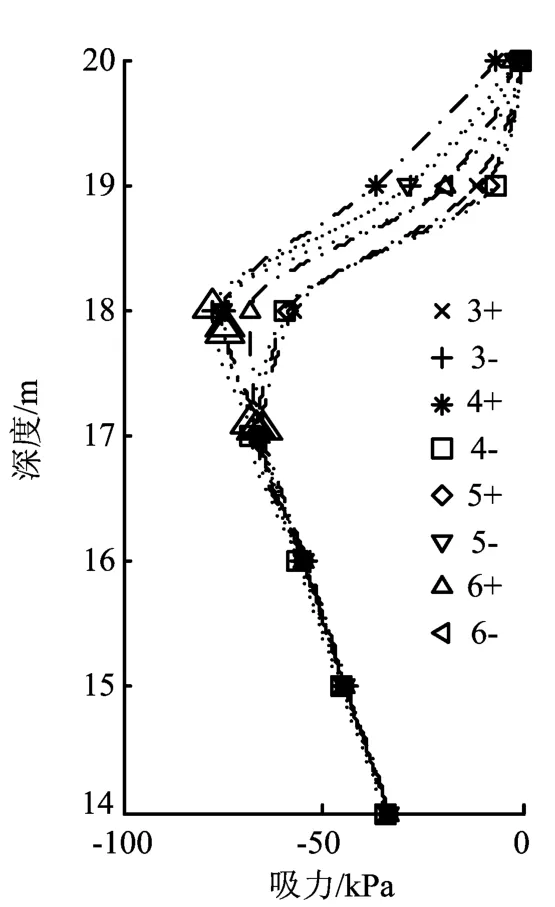
图7 参数变异性对土体吸力－深度关系的影响

由图7可以求得相应的吸力降低深度与水力参数的关系，如图8所示，图8中水平线段表示参数取均值时的吸力降低深度，正、负号分别代表参数Xi取上限及下限时的情况。由图8可见，在4个水力参数中，a及n对的变异性对Ds的影响较大，而Sr及ks的变异性对Ds的影响则相对较小。其中，参数a增大时Ds也增大，反之则使Ds减小；但是，这种变化是非线性的，a的增加使Ds增大的程度更大。参数n对Ds的影响与参数a的影响正好相反，n值增大时Ds会略有减小，而n值减小时Ds会增加很多。参数Sr及ks对Ds的影响规律一致：Sr或ks增加时，Ds增加；反之，Sr或ks减小时，Ds减小。

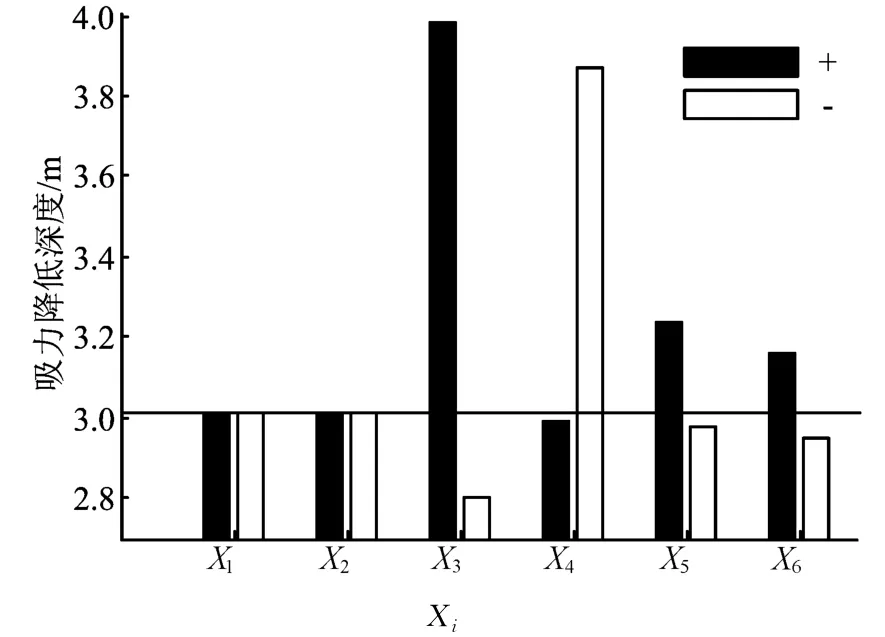
图8 参数变异性对吸力降低深度Ds的影响

2.3.2 参数变异性对边坡安全系数的影响

考虑强度参数及水力参数变异性时，各组参数对应的边坡安全系数Fs如图9所示。

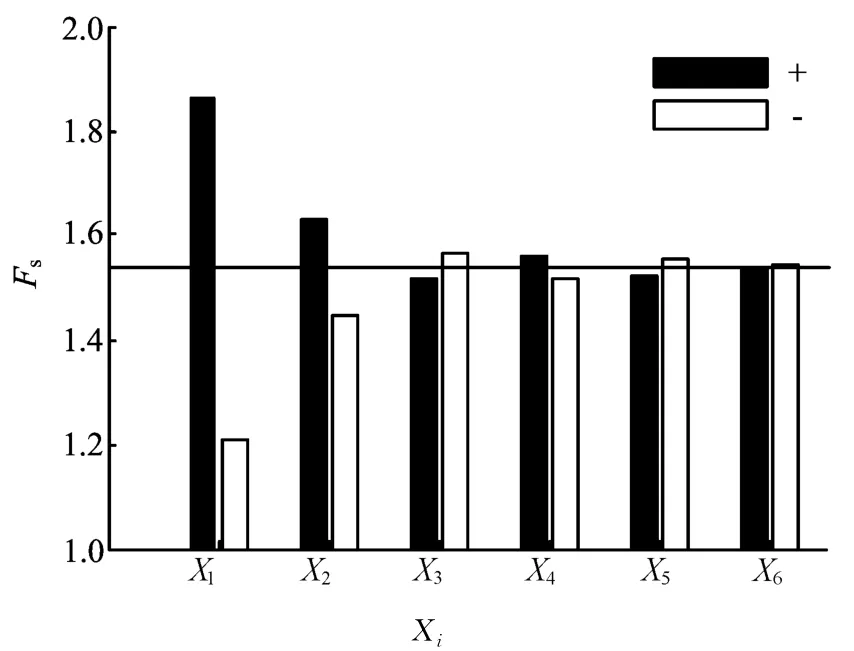
图9 参数变异性对边坡安全系数的影响

图9中水平线段表示参数取均值时的安全系数。可见，各参数分别在各自的均值附近按1倍均方差上下波动时，强度参数对安全系数有很大影响，而水力参数对安全系数的影响则相对较小。在4个水力参数中，a及n的变异性对安全系数的影响相对较大，Sr及ks对安全系数的影响相对较小。其中，参数a增大时，Fs降低；a减小时，Fs增大；n增大时，Fs增大；n减小时，Fs降低；Sr增大时，Fs减小；Sr减小时，Fs增大；ks增大时，Fs减小；ks减小时，Fs不变。但是，水力参数对Ds的影响程度与对Fs的影响程度并不完全一致，这是因为图8只是对应于特定研究剖面，而图9的Fs对应于整个边坡。

由图9还可以看出，水力参数中，a及n的变异性对安全系数的影响程度较为一致，它们的影响程度大于Sr及ks的变异性的影响。而由表1可知，Sr及ks的变异系数很大，n的变异系数最小。可以推测，若这几个水力参数的变异水平相同，则参数n的变异性对边坡安全系数的影响最大，其次是a的变异性的影响，而参数Sr及ks的变异性对边坡安全系数的影响则相对很小，可以忽略不计。

2.3.3 参数变异性对边坡潜在滑面位置的影响

考虑强度参数及水力参数变异性时，各组参数对应的边坡滑动面如图10所示，图中实线为所有参数取均值时对应的滑面位置。

图10 参数变异性与边坡潜在滑动面的关系

由图10可见，力学参数中，黏聚力c′的增大使滑动面位置变深，而内摩擦角φ′的增大则使滑动面位置变浅。水力参数中，n的增大会导致边坡滑动面位置变深，其他3个水力参数的增大则使滑面位置略微变浅；水力参数减小时，滑面位置都变深。其中，n增大或减小时边坡滑面位置均变深，且滑面位置变化幅度在水力参数中最大，因而n值与滑面位置呈非线性关系，这与n在土水特征曲线中反应曲线的斜率有关。在本算例中，强度参数变异性对滑面位置的影响大于水力参数变异性的影响，这与参数n的变异系数较小有关。

3 结 论

（1）根据吸力－深度关系曲线，定义了吸力降低深度，分析了吸力降低深度与边坡安全系数及滑动面位置的对应关系。

（2）总降雨量一定时，不同降雨模式对边坡稳定性的影响与边坡土体本身的渗透能力有关。当饱和渗透系数较大时，降雨模式对边坡安全系数及潜在滑动面位置的影响几乎相同；当饱和渗透系数较小时，长时间小强度的降雨对边坡安全系数及潜在滑面位置的影响大于短时间强降雨的影响。

（3）力学参数的变异性对边坡安全系数及潜在滑动面位置的影响大于水力参数变异性的影响。水力参数中，土水特征曲线拟合参数a及n的影响相对较大。

本文在进行降雨入渗条件下非饱和土质边坡的稳定性分析时，没有考虑非饱和土的膨胀性。膨胀土是一种典型的非饱和土，在降雨作用下，膨胀土将产生体积膨胀，并反过来影响膨胀土的土水特征及边坡中的水压和应力分布。这些问题需要进行深入研究。

［1］ Thomas H R，He Y.A coupled heat－moisture transfer theory for deformable unsaturated soil and its algorithmic implementation［J］.International Journal for Numerical Methods in Engineering，1997，40（18）：3421－3441.

［2］ Wong T T，Fredlund D G，Krahn J.A numerical study of coupled consolidation in unsaturated soils［J］.Canadian Geotechnical Journal，1998，35（6）：926－937.

［3］ 徐 晗，朱以文，蔡元奇，等.降雨入渗条件下非饱和土边坡稳定分析［J］.岩土力学，2005，26（12）：1957－1962.

［4］ 徐 全，谭晓慧，沈梦芬.降雨入渗条件下土质边坡的稳定性分析［J］.岩土工程学报，2012，34（Z1）：254－259.

［5］ 毕卫华，谭晓慧，王 伟，等.RBFN及SVM在边坡稳定可靠度分析中的应用［J］.合肥工业大学学报：自然科学版，2011，34（7）：1035－1039.

［6］ Tsaparas I，Rahardjo H，Toll D G，et al.Controlling parameters for rainfall－induced landslides［J］.Computers and Geotechnics，2002，29（1）：1－27.

［7］ Leong E C，Rahardjo H.Review of soil－water characteristic curve equations［J］.Journal of Geotechnical and Geoenvironmental Engineering，1997，123（12）：1106－1117.

［8］ Liu Z，Yan Z，Duan J，et al.Infiltration regulation and stability analysis of soil slope under sustained and small intensity rainfall［J］.Journal of Central South University，2013，20（9）：2519－2527.

［9］ Shin H，Kim Y T，Park D K.Development of rainfall hazard envelope for unsaturated infinite slope［J］.KSCE Journal of Civil Engineering，2013，17（2）：351－356.

［10］ 黄润秋，戚国庆.非饱和渗流基质吸力对边坡稳定性的影响［J］.工程地质学报，2002，10（4）：343－348.

［11］ 吴俊杰，王成华，李广信.非饱和土基质吸力对边坡稳定性的影响［J］.岩土力学，2004，25（5）：732－744.

［12］ Ng C W W，Shi Q.A numerical investigation of the stability of unsaturated soil slopes subjected to transient seepage［J］.Computers and Geotechnics，1998，22（1）：1—28.

［13］ Kim J，Jeong S，Park S，et al.Influence of rainfall－induced wetting on the stability of slopes in weathered soils［J］.Engineering Geology，2004，75（3）：251－262.

［14］ Rahardjo H，Ong T H，Rezaur R B，et al.Response parameters for characterization of infiltration［J］.Environmental Earth Sciences，2010，60（7）：1369－1380.

［15］ 刘 波.FLAC原理、实例与应用指南［M］.北京：人民交通出版社，2005：46－58.

［16］ Tan X H，Wang J G.Nonlinear finite element reliability analysis and sensitivity analysis of slope stability ［J］.Geotechnical Engineering，2009，40 （1）：17－23.

［17］ Tan X H，Wang J G.Nonlinear finite element reliability analysis of slope stability［C］／／Proceedings of the 2nd International Conference on Geotechnical Engineering for Disaster Mitigation and Rehabilitation （GEDMAR08）.New York：Springer－Verlag，2008：565－571.

［18］ Fredlund D G，Houston S L.Protocol for the assessment of unsaturated soil properties in geotechnical engineering practice［J］.Canadian Geotechnical Journal，2009，46（6）：694－707.

［19］ 陈 伟，孔令伟，郭爱国，等.吸力对弱膨胀土强度贡献的试验 研 究 与 预 测 分 析 ［J］.岩 土 力 学，2008，29（7）：1783－1787.

［20］ Fredlund D G，Rahardjo H.非饱和土力学［M］.陈仲颐，张在明，陈愈炯，等，译.北京：中国建筑工业出版社，1997：313－321.

［21］ 谭晓慧，王建国.边坡的弹塑性有限元可靠度分析［J］.岩土工程学报，2007，29（1）：44－50.