寒冷地区混凝土箱梁温度场研究

孙维刚， 陈永瑞， 刘来君， 武群虎， 于杨龙

（1.长安大学 公路学院，陕西 西安 710064；2.中铁二十局集团第六工程有限公司，陕西 西安 710032）

预应力混凝土箱梁结构受力性能优越、建造简单，是目前公路桥梁的常见结构形式。国内外工程研究人员对混凝土箱梁裂缝产生的原因分析表明，混凝土箱梁的温度应力可以达到甚至超过汽车荷载产生的应力，造成营运中箱梁的某些部位开裂［1］。混凝土箱梁的温度分布受到气象因素（太阳辐射、夜间降温、寒流、风、雨、雪等）、桥址纬度、结构方位等外界条件的影响，同时，也受到材料性质、结构形状、表面颜色等内部因素的影响。

近年来，国内外工程研究人员基于理论分析和现场温度观测，对温度场进行了大量的研究工作［2－8］，认为混凝土箱梁的温度场分布随时间的变化（简称“温度时程”）规律与箱内外环境温度的变化规律较为类似，基本呈正弦曲线变化，变化周期与环境温度变化周期一致，箱梁截面的温度分布为非线性分布。采用不同的温度梯度模式对温度应力计算结果影响较大［9］。各国规范制定了适合于本国环境条件的温度梯度计算模式。我国公路规范［10］考虑了均匀温度作用和梯度温度作用对桥梁结构的影响。混凝土箱梁温度场是内部因素和外部环境综合作用的结果，研究特定环境条件下桥梁结构的温度场，从而掌握本地区桥梁结构的温度规律，对同类地区设计、施工以及桥梁状态分析，都有重要的意义。

1 温度场观测

1.1 工程概况

古浪地理坐标为北纬37°09′～37°54′、东经102°38′～103°54′，属祁连山高寒亚干旱区和河西冷温干旱区。柳条河大桥为等高度且左右幅分离独立的预应力混凝土预制连续箱梁，纵向为南北走向。大桥右线，最大桥高14.8m，上部结构采用16×30m连续箱梁，全桥分为3联；大桥左线，最大桥高13m，上部结构采用14×30m连续箱梁，亦为3联。箱梁L／2截面顶板厚度为18cm；翼缘板根部厚度为25cm，端部厚度为18cm；腹板和底板厚度分别为18cm。箱梁混凝土强度等级为C50。

1.2 测点布置

选取跨中截面为观测截面，测点布置如图1所示。采用3种不同测试仪器，测点编号具体说明见1.3。

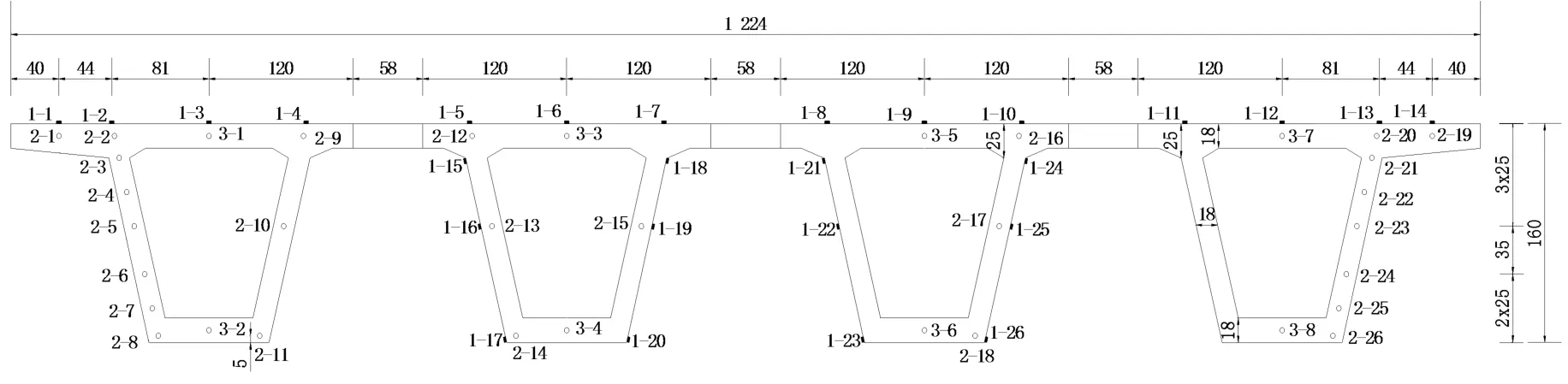
图1 测点布置图（单位：cm）

1.3 实验仪器

（1）混凝土表面温度测点（“1－”测点）。采用UT302B非接触红外测温仪观测，测温范围为：－32～550℃，显示精度为±1.8℃或±1.8%t（t为温度）。

（2）混凝土内部温度测点（“2－”测点）。传感器采用WRN型分度号K热电偶温度计，测温范围为－50～400℃，测温精度为0.75%t±2.5。测试仪器采用TES－1310数字式温度表，解析度为0.1℃，温度测量范围为－50～199.9℃，温度测量精度为±（0.3%t＋1）。

2 温度时程分析

2.1 日温差分析

为了确定箱梁温度时程规律，对观测了20d（2010年12月2日至2011年8月1日）代表性测点（编号：1－1、1－2、1－3、1－4、2－1、2－2、3－1、2－9、2－5、2－10、2－8、3－2、2－11）的观测结果做了如下统计：对各测点的日温差（测点在测试日期内不同时刻的温度差）进行计算，再从各测点的日温差中找出最值，发现以上测点出现日温度差最小值的时间为2011年1月6日（冬季），出现日温度差最大值的时间为2011年5月16日（夏季）。对测点的日温差最值进行统计，见表1所列。

表1 日温差最值℃

从表1最大值数据可以看出，日温差最大值从顶板到底板依次降低。箱梁顶板外表面日温差最大值均值可达到36.73℃，底板内部日温差最大值均值仅为14.33℃。而日温差最小值沿箱梁高度方向的变化不大，规律性不明显。

选择日温差最值出现时期的温度进行分析研究，对同一水平面上的测点取平均值，对顶板表面（测点1－1、1－2、1－3、1－4温度均值）、顶板内部（测点2－1、2－2、3－1、2－9温度均值）、腹板内部（测点2－5、2－10温度均值）、底板内部（测点2－8、3－2、2－11温度均值）的温度时程变化进行分析研究。

2.2 时程分析

根据最小二乘法原理，对实测温度的时程变化进行拟合，从而确定箱梁各位置的温度时程规律。对各位置的温度时程曲线进行观察，发现其具有明显的周期性，并通过对比分析多种函数模型的拟合优度，最终采用傅里叶函数进行拟合。假设温度时程变化函数为：

其中，y为温度；a、b、c、w为待定常数；x为时刻。

各代表性位置的拟合结果如图2、图3所示。

从图2a可以看出，2011－01－06顶板外表面温度实测最大值出现在13：00左右，而拟合的最大值在13：00—14：00之间，相差不大。从图2b可以看出，2011－01－06顶板内部早晨温度实测值和拟合值相差较小，趋势一致，而在下午内部温度变化较为平缓，和拟合值的曲线走势有一定的偏差，但偏差值最大为0.7℃，仅为实测值的5.5%。

从图2c、图2d可以看出，2011－01－06腹板内部温度、底板内部温度实测最大值出现的时刻和拟合最大值出现的时刻相差不大，图形整体趋势一致，拟合效果良好。

中国特色社会主义进入新时代，党的十九大在新的历史起点上对新时代坚持和发展中国特色社会主义作出重大战略部署。为了适应新形势、吸纳新经验、确认新成果，现行宪法进行了第五次修改，作出新的调整。这次修改把党的十九大确定的重大理论观点、方针政策和一系列治国理政新理念新思想新战略特别是习近平新时代中国特色社会主义思想载入国家根本法，对党和国家事业发展具有十分重要的意义，对中国宪法学的繁荣发展同样具有划时代的伟大意义，使宪法学研究可以在中国语境和时代特点下，通过本土化的知识提炼和原创性的理论贡献，构建起具有中国特色的社会主义宪法学体系。

从图3a可以看出，2011－05－16顶板表面拟合温度最大值出现的时刻和实测温度最大值出现的时刻一致，都在15：00左右。

从图3b可以看出，顶板内部实测温度最小值出现在早上8：00左右，顶板内部实测温度最大值出现在17：00左右，比顶板表面晚约2h，拟合值和实测值贴近，偏差较小。

从图3c、图3d可以看出，2011－05－16腹板内部温度、底板内部温度实测最大值出现的时刻和拟合最大值出现的时刻相差不大，实测值均匀分布于拟合曲线两侧，变化趋势一致。

综上所述，采用傅里叶函数对温度时程进行拟合，具有很好的拟合效果，箱梁各位置温度时程拟合函数见表2所列。

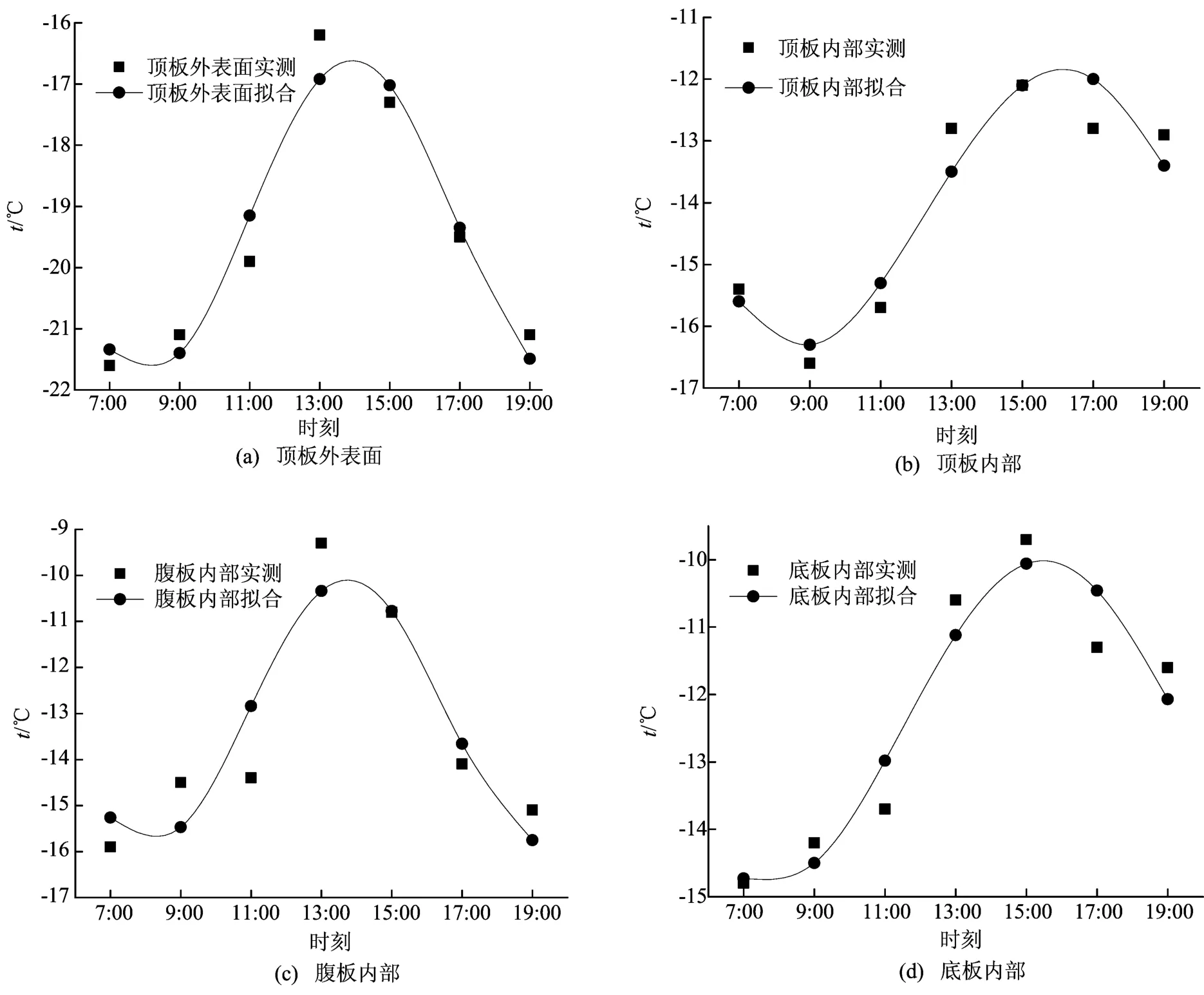
图2 4个代表性位置2011－01－06温度时程拟合曲线

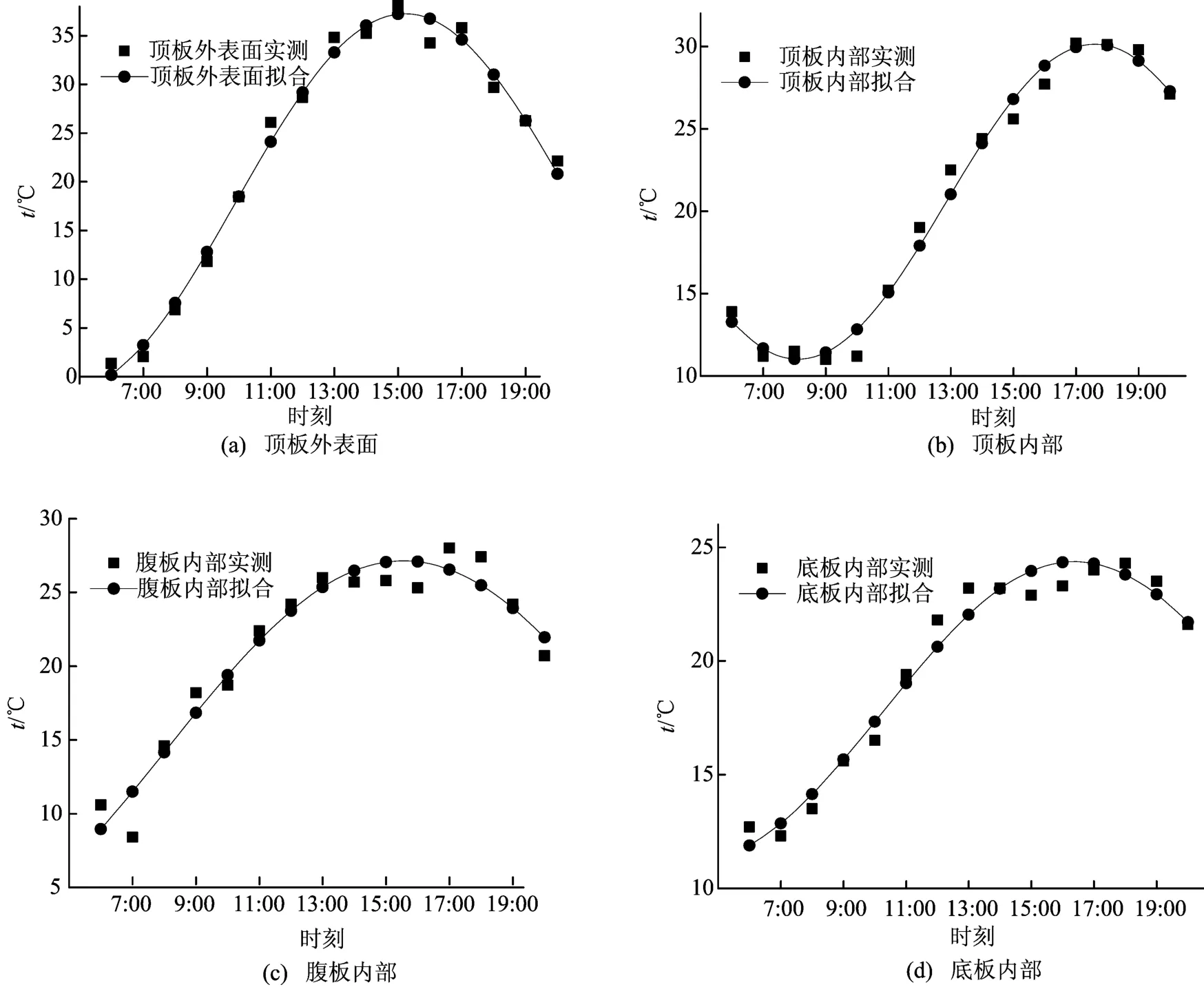
图3 4个代表性位置2011－05－16温度时程拟合曲线

表2 温度时程拟合函数

以上对同一截面，不同时期的温度时程规律进行了拟合分析。分析发现，采用傅里叶函数拟合箱梁的日温度时程规律可以得到较准确的拟合结果。箱梁结构在15h内的温度时程分布可以用单个对应的傅里叶函数来表示，而2个时期（2011－01－06和2011－05－16）的温度时程拟合函数的傅里叶常数是不同的。因此，不能用单个傅里叶函数来表达箱梁结构长期的温度时程规律。

3 温度分布分析

3.1 温度分布差最大值

分别对1＃～4＃梁的温度分布差（同一时刻下不同测点之间的温度差）进行统计分析，从而确定各单片梁温度分布差最大值及其出现的时间，见表3所列。

从表3可以看出，边梁的温度分布差大于中梁，这是由于边梁易受到日照作用的影响，而中梁受边梁的遮挡，日照作用不明显。下午15：00和16：00的温度分布差最大。

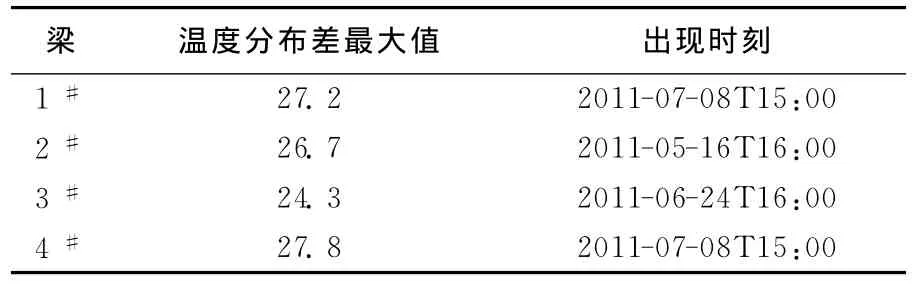
表3 温度分布差最大值统计 ℃

3.2 竖向温度梯度拟合

从以上分析可知，边梁的温度差最大，故选择边梁进行温度梯度研究。研究桥梁的竖向温度梯度，将同一水平面上的测点温度进行平均，计算沿梁高的桥梁温度梯度，选择测试温度梯度最大值进行研究，不考虑均匀温升。

各国规范根据本国实际环境条件，对竖向温度梯度模式进行了规定，各国规定的竖向梯度模式中，美国公路桥梁设计规范 AASHTO－2005［11］、欧洲规范 EN 1991－1－5［12］和我国公路桥涵设计通用规范JTG D60－2004［10］均采用双折线模式，新西兰桥梁规范 NZBM－2003［13］采用5次幂函数模式，而我国铁路桥涵设计规范TB 10002.3－2005［14］是以e为底的指数函数模式。且NZBM－2003和EN 1991－1－5考虑了梁底温差。借鉴文献［14］的温度分布模式，采用如下拟合函数对实测值进行拟合：

其中，ty为计算点处的温差；t0为箱梁截面沿梁高方向的最大温差；y为计算点至箱梁外表面的距离；b为待定参数。

从（2）式中可以看出，最大温差值和待定常数值决定整个箱梁断面的温差分布形式。将实测的温度梯度按最小二乘法进行拟合，从而求得竖向温度梯度分布的函数规律。根据2011年7月8日观测数据分别求得的t0值和b值见表4所列，其对应的温度梯度分布图如图4所示。

表4 温度梯度拟合结果

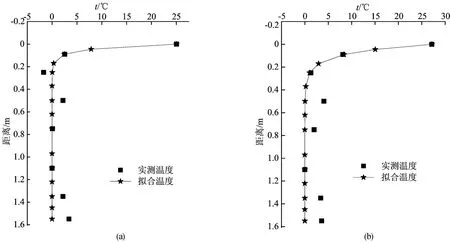
图4 1＃、4＃梁竖向温度梯度分布

从图4可以看出，参考面（全截面中温度最低的截面部分）以上位置，采用指数函数拟合，能够取得良好的效果，但是在接近底板下表面的测点位置，实测温度值普遍高于拟合温度值。

而我国公路规范［10］，将底板部分的温度梯度简化为0℃，这不能准确地体现该地区箱梁温度场分布。

4 温度场对混凝土箱梁的影响

目前，对于温度作用，主要分为日照、骤然降温、年温度变化3种类型。基于以上研究，根据时间和空间变化，又可将温度作用分为温度时变作用和温度分布作用2种类型。

寒冷地区往往日温差较大，这导致混凝土箱梁结构短时间内的温度变化也较大，尤其在气温骤变的情况下，在混凝土箱梁中产生温度冲击作用。这种温度冲击作用对新浇筑混凝土的影响尤为明显。

混凝土箱梁温度分布作用是其瞬时的温度梯度对其结构的影响，这种作用出现的主要原因是桥梁结构运营过程中的日照作用。选取准确的箱梁温度梯度计算参数是准确计算温度梯度应力的关键。因此，在设计过程中，应该根据当地的实际温度变化情况，选取合适的温度梯度设计参数，从而精确计算混凝土箱梁的温度应力，降低混凝土箱梁产生温度裂缝的概率。

5 结 论

基于寒冷地区现场温度场观测，从温度时变和温度分布2个方面研究了温度场规律。

（1）针对各测点实测温度时程曲线明显的周期性特点，根据最小二乘法原理，对实测温度的时程变化进行拟合，采用傅里叶函数得到了贴近实测值的拟合结果。

（2）对同一截面、不同时间的温度时程分布进行了拟合分析，发现箱梁结构在15h内的温度时程分布可以用单个对应的傅里叶函数来表示，而2个时期（2011－01－06和2011－05－16）的温度时程拟合函数的傅里叶常数是不同的，因此不能用单个傅里叶函数来表示箱梁结构长期的温度时程规律。

（3）我国规范对混凝土箱梁地板温度梯度简化为0℃，而实测发现，混凝土箱梁存在底板温度梯度，在该地区其值可达到3℃。

［1］ 叶见曙，贾 琳，钱培舒.混凝土箱梁温度分布观测与研究［J］.东南大学学报：自然科学版，2002，32（5）：788－793.

［2］ 方 志，汪 剑.大跨预应力混凝土连续箱梁桥日照温差效应［J］.中国公路学报，2007，20（1）：62－67.

［3］ 张亮亮，杨 磊，杨转运，等.大跨混凝土箱梁温度场分析［J］.土木建筑与环境工程，2011，33（1）：36－42.

［4］ Norris A，Saafi M，Romine P.Temperature and moisture monitoring in concrete structures using embedded nanotechnology／microelectromec－hanical systems（MEMS）sensors［J］.Construction and Building Materials，2008，22 （2）：111－120.

［5］ 王 毅.预应力混凝土连续箱梁温度作用的观测与分析研究［D］.南京：东南大学，2006.

［6］ 丁幼亮，王高新，周广东，等.基于现场监测数据的润扬大桥斜拉桥钢箱梁温度场全寿命模拟方法［J］.土木工程学报，2013，46（5）：129－136.

［7］ 叶见曙，雷 笑，王 毅.基于统计分析的混凝土箱梁温差标准值研究［J］.公路交通科技，2009，26（11）：50－54.

［8］ 孙 君，李爱群，丁幼亮.润扬长江大桥钢箱梁的温度分布监测与分析［J］.公路交通科技，2009，26（8）：94－98.

［9］ 何 翔，方诗圣，方 飞，等.不同梯度温度作用下曲线桥梁的温度效应分析［J］.合肥工业大学学报：自然科学版，2012，35（8）：1088－1092.

［10］ JTG D60－2004，公路桥涵设计通用规范［S］.

［11］ AASHTO LRFD bridge design specifications，SI units［S］.3rd ed.American Association of State Highway and Transportation Officials，2005.

［12］ EN 1991－1－5：2003，Eurocode 1：actions on structures－partⅠ－5：general actions－thermal actions［S］.European Committee of Standardization，2003.

［13］ Bridge manual，section 3：design loading［S］.2nd ed.New Zealand Transport Agency，2003.

［14］ TB 10002.3－2005，铁路桥涵钢筋混凝土和预应力混凝土结构设计规范［S］.