功能梯度中厚板切口奇性分析

程长征， 丁 昊， 周 伟， 韩志林

（合肥工业大学 土木与水利工程学院，安徽 合肥 230009）

0 引 言

功能梯度材料是一类组成结构和性能在材料厚度或长度方向连续或准连续变化的非均质复合材料。由于中间成分的连续变化消除了材料中的宏观界面，功能梯度材料整体表现出良好的热应力缓和特性［1］。板、壳和梁仍然是功能梯度材料结构的主要形式。板材中由于加工或拼装会形成各种形式的切口，其尖端存在严重的应力集中（实为应力奇异）现象，会影响功能梯度材料结构的安全性能［2］。

文献［3］研究了均质平面板切口尖端弹性应力场的解析表达；文献［4］分析了板的厚度对板内切口尖端应力奇异状态的影响；文献［5］给出了角度非均质材料平面切口尖端的渐近场；文献［6］研究了功能梯度多材料接头处的应力奇异性，采用解析和数值2种方法对降低功能梯度材料切口尖端的奇异性进行了研究；文献［7］研究了功能梯度拉伸板和弯曲梁切口尖端应力场；文献［8］运用平均应变能密度准则对功能梯度材料含切口构件在Ⅰ型荷载作用下的断裂性能进行了分析；文献［9］研究了含孔洞的功能梯度板受反平面剪切时切口尖端的应力集中因子；文献［10］提出了一种计算功能梯度材料平板切口尖端J积分的数值方法；文献［11］研究了功能梯度薄板切口尖端奇异性和边界层效应。

另外，文献［12－14］用特征展开法研究了功能梯度薄板、高阶板以及三阶板切口尖端应力奇性指数和特征角函数的计算表达式，但给出的是一组超越方程，通过一般方法求得其解析解是非常困难的。

本文提出引入切口尖端位移渐近展开假设，将板的平衡方程及边界条件转化为特征微分方程，采用插值矩阵法［15］求解，可以一次性地计算出功能梯度中厚板切口各阶奇性指数及其相应的特征角函数。

1 切口奇性特征方程组的建立

功能梯度板切口示意图如图1所示，该功能梯度中厚板材料的弹性模量E（z）沿板的厚度方向z变化，泊松比μ设为常数，板内含有一开角为α的切口。

本文采用Reissner中厚板理论，板的变形可以用3个独立的广义位移分量描述，即中面挠度w、变形前垂直于中面的直线段分别在oρz与oθz平面内的转角uρ、uθ。板内任意一点的位移分量随板厚线性变化，挠度与厚度坐标无关，具体表达式为：

图1 功能梯度板切口

柱坐标系下的几何方程为：

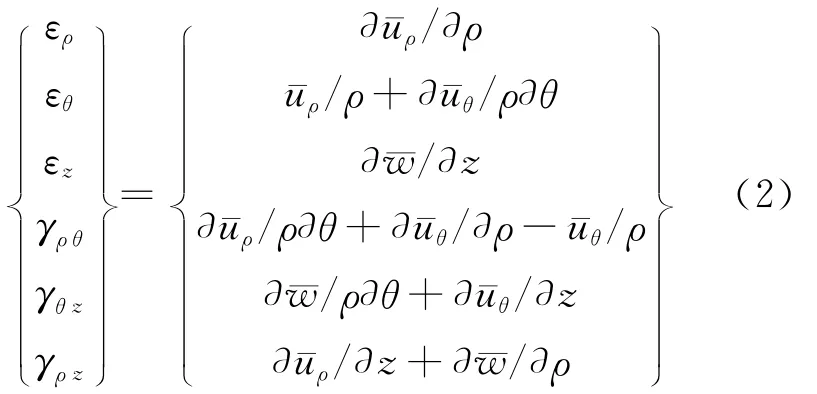
将（1）式代入（2）式可得：

平面应力问题的本构方程为：

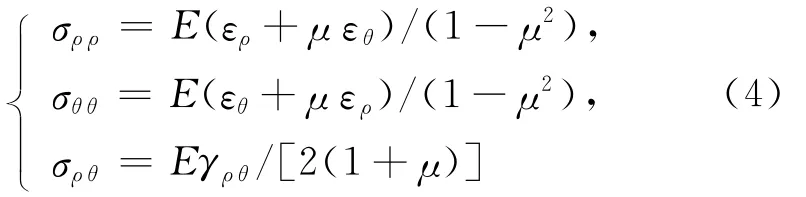
将应变分量（3）式代入（4）式，可得板面内应力分量的表达式为：

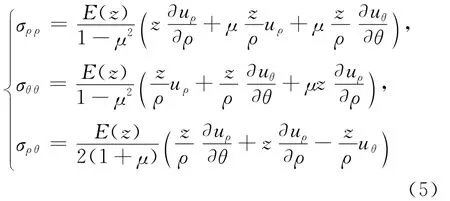
按能量等效原则可得板的横向切应力σρz和σθz分别为：

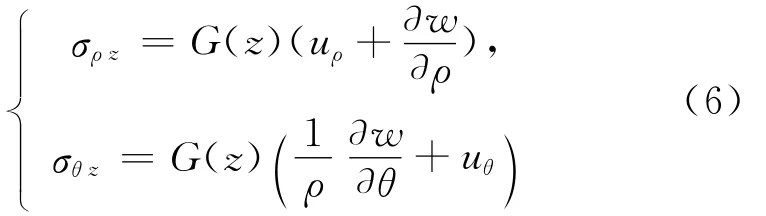
其中，G（z）为剪切模量。

板内的弯矩（mρ，mθ，mρθ）、剪力（Qρ，Qθ）与应力之间的关系为：

其中，h为板厚。

记

将（5）式、（6）式代入（7）式，板内弯矩和剪力的表达式为：

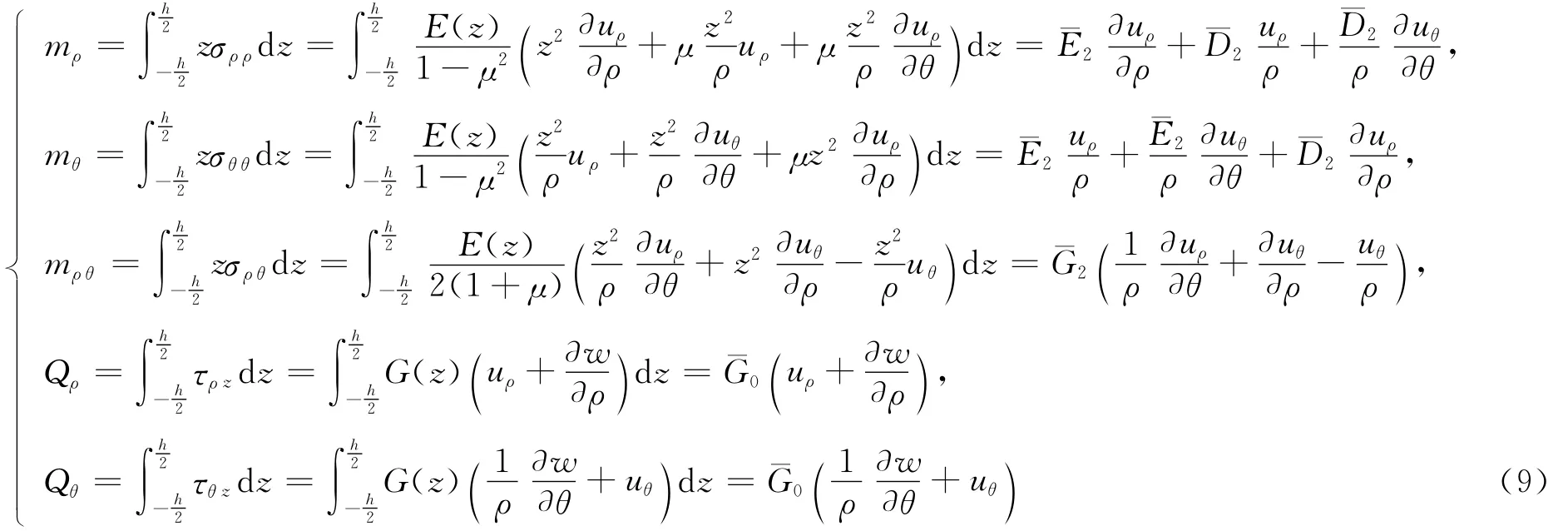
不计体力时，板的平衡微分方程为：

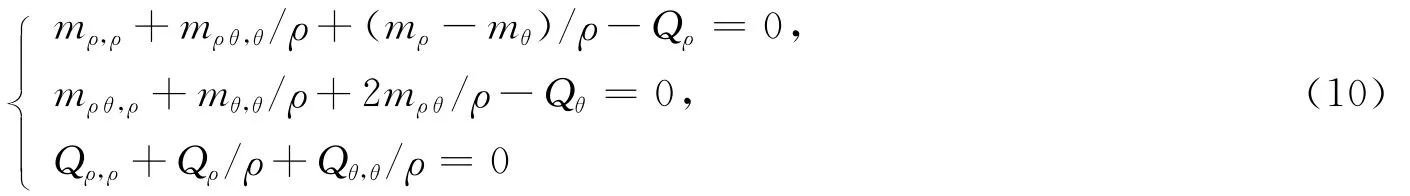
将（9）式代入（10）式可得：

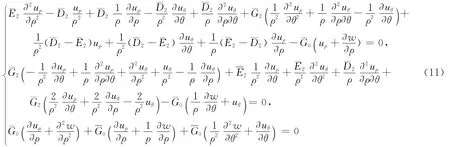
将切口尖端的位移场取如下的级数渐近展开［12］，即

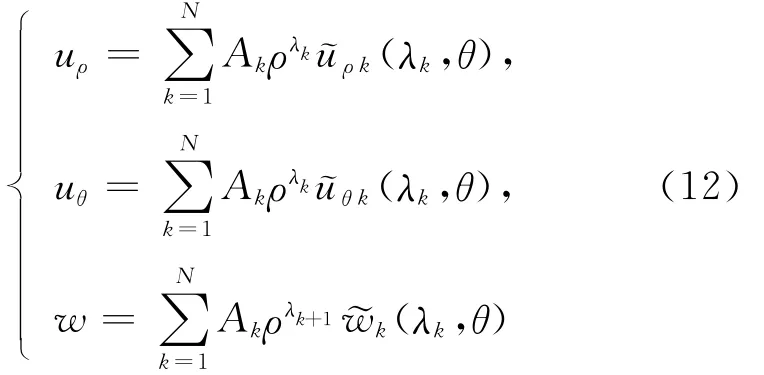
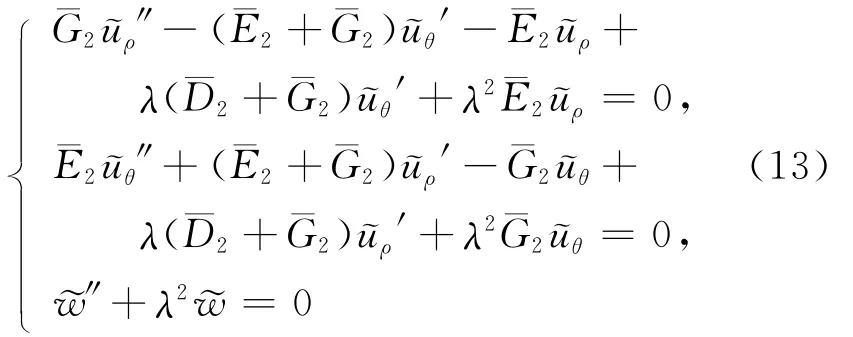
由（8）式可得：

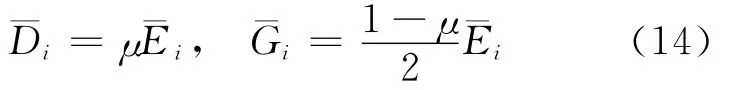
其中，i＝0，1，2。因此，（13）式可转化为切口奇性特征方程组，即

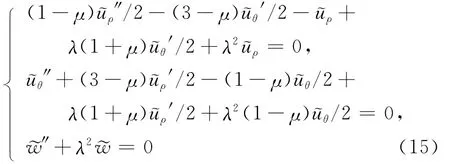
由于采用了Reissner中厚板假设和（14）式，所以最终的切口特征微分方程组与材料的弹性模量没有关系，即板厚方向不同的材料梯度模式对切口的奇性特征方程没有影响。

2 切口径向边界条件

若切口的两径向边界上面力自由，则可得自由边界条件为：

将（12）式的典型项代入（16）式可得：

由于（14）式的关系存在，（17）式可转化为：

若切口的两径向边为夹支，则有夹支边界条件如下：

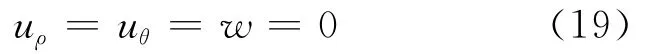
取（12）式的典型项代入（19）式可得：

若切口的两径向边为简支，则有简支边界条件如下：

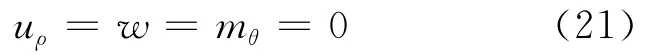
取（12）式的典型项代入其中，可将其转化为：

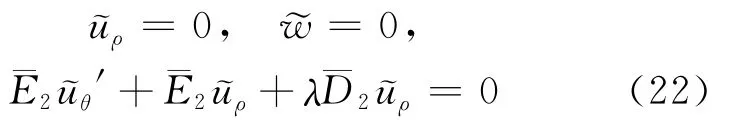
由于（14）式，（22）式可以转化为：

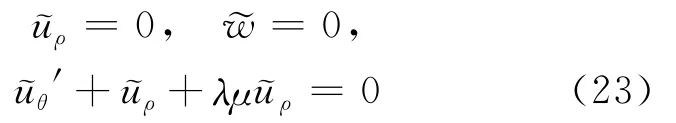
至此，将切口的各类径向边界条件转化为切口特征角函数与奇性指数的组合形式。

3 数值求解及算例

由于切口奇性特征微分方程组（13）式中含有λ2项，是一个非线性特征值问题，直接求解需要采用迭代算法。现引入：

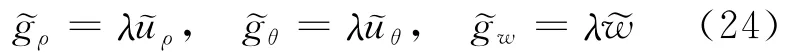
将（13）式的非线性特征方程组转化为线性方程组，即

从而，功能梯度板切口奇性分析转化为在边界条件（18）式、（20）式、（23）式下，求解特征微分方程组（24）式、（25）式的问题，像龙格 －库塔等一般的数值方法即可求解，本文利用插值矩阵法［15］，一次性地计算出切口所有的奇性指数λ和相应的特征角函数～uρ和～uθ。

自由－自由边界条件下切口的应力奇性指数计算结果见表1所列。

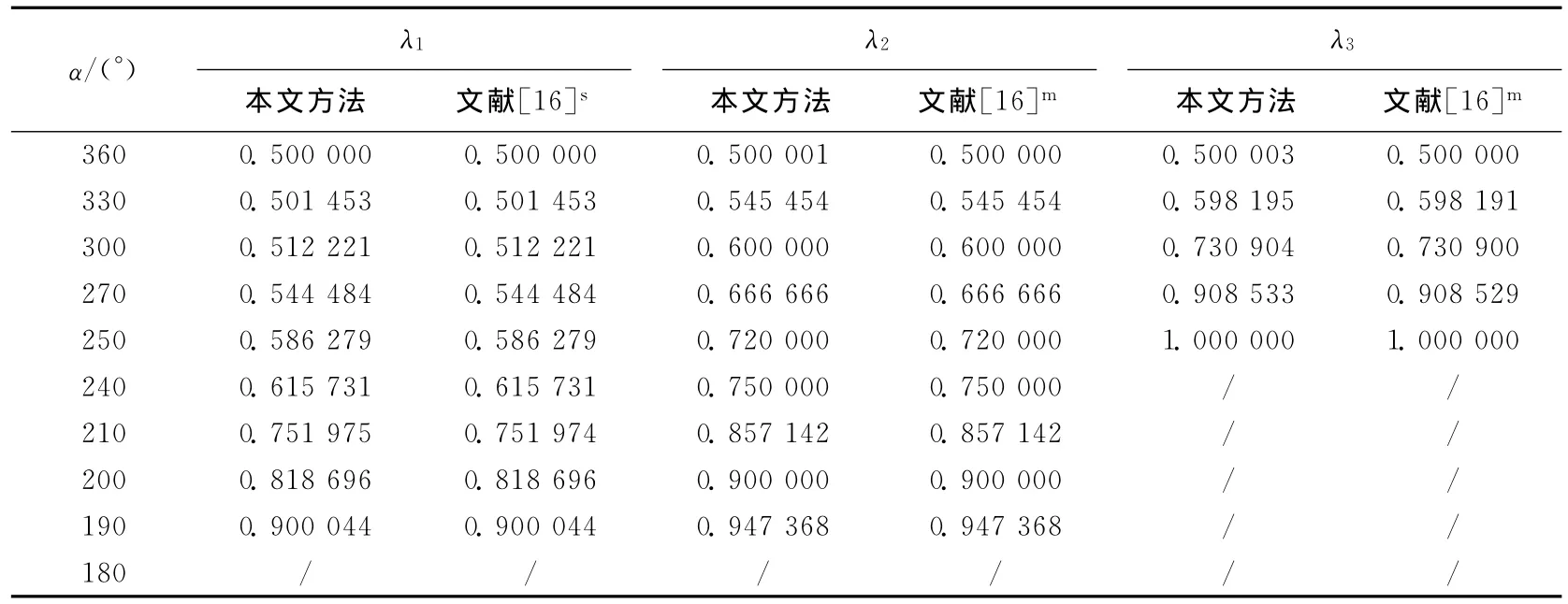
表1 自由－自由边界条件下的切口应力奇性指数

从（5）式、（6）式可知，当λ＜1时应力才奇异，从（13）式可知，λ＞0才能满足位移分量的正则化条件，因此表1中只列出奇性指数为0～1的值。计算发现，α＞250°的切口存在3个奇性指数，α在（180°，250°）之 间 的 切 口 存 在 2 个 奇 性 指 数，α＜180°的切口不发生奇异。文献［16］采用特征展开法获得了一组关于奇性指数的超越方程，但没有解析解，本文采用牛顿迭代法。由表1可看出，本文方法与文献［16］方法的计算结果能吻合到小数点后5位，文献［16］方法需要将矩奇异和剪切奇异分开计算，而本文方法可以一次性地计算出所有的奇性指数。

当α＝360°时，切口退化为裂纹问题，裂纹的3个奇性指数分别对应的特征角函数如图2所示。图2a中只有特征角函数～w而没有～uρ和～uθ，结合（8）式，说明奇性指数λ1对应的是剪切奇异；图2b和图2c中只有特征角函数～uρ和～uθ而没有～w，说明奇性指数λ2和λ3对应的是矩奇异。通过这种方法可以将已经计算出的奇性指数所对应的 矩奇异和剪切奇异区分开。

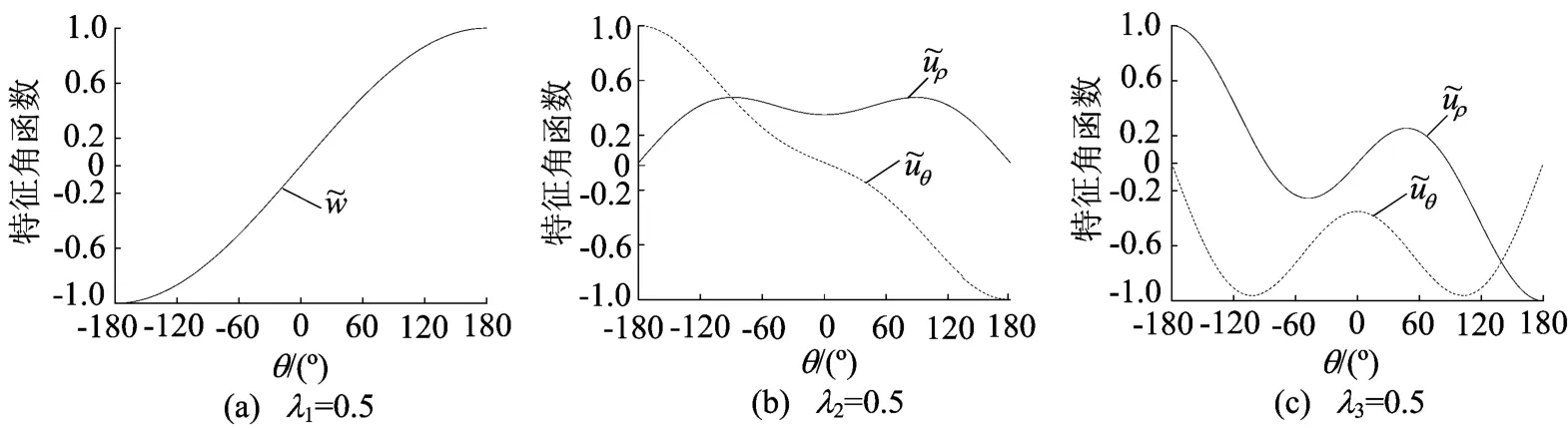
图2 α＝360°时不同应力奇性指数对应的特征角函数

夹支－夹支、简支－简支边界条件下不同切口开角时切口的应力奇性指数见表2所列，由表2可知本文结果与文献［16］结果很好吻合，2种边界条件下，α＞180°时发生奇异，且奇性指数均为3个。由特征角函数分析可知，夹支－夹支边界条件下第1个奇性指数对应剪切奇异，后2个对应矩奇异；简支－简支边界条件下第1和第3个奇性指数对应矩奇异，第2个对应剪切奇异。

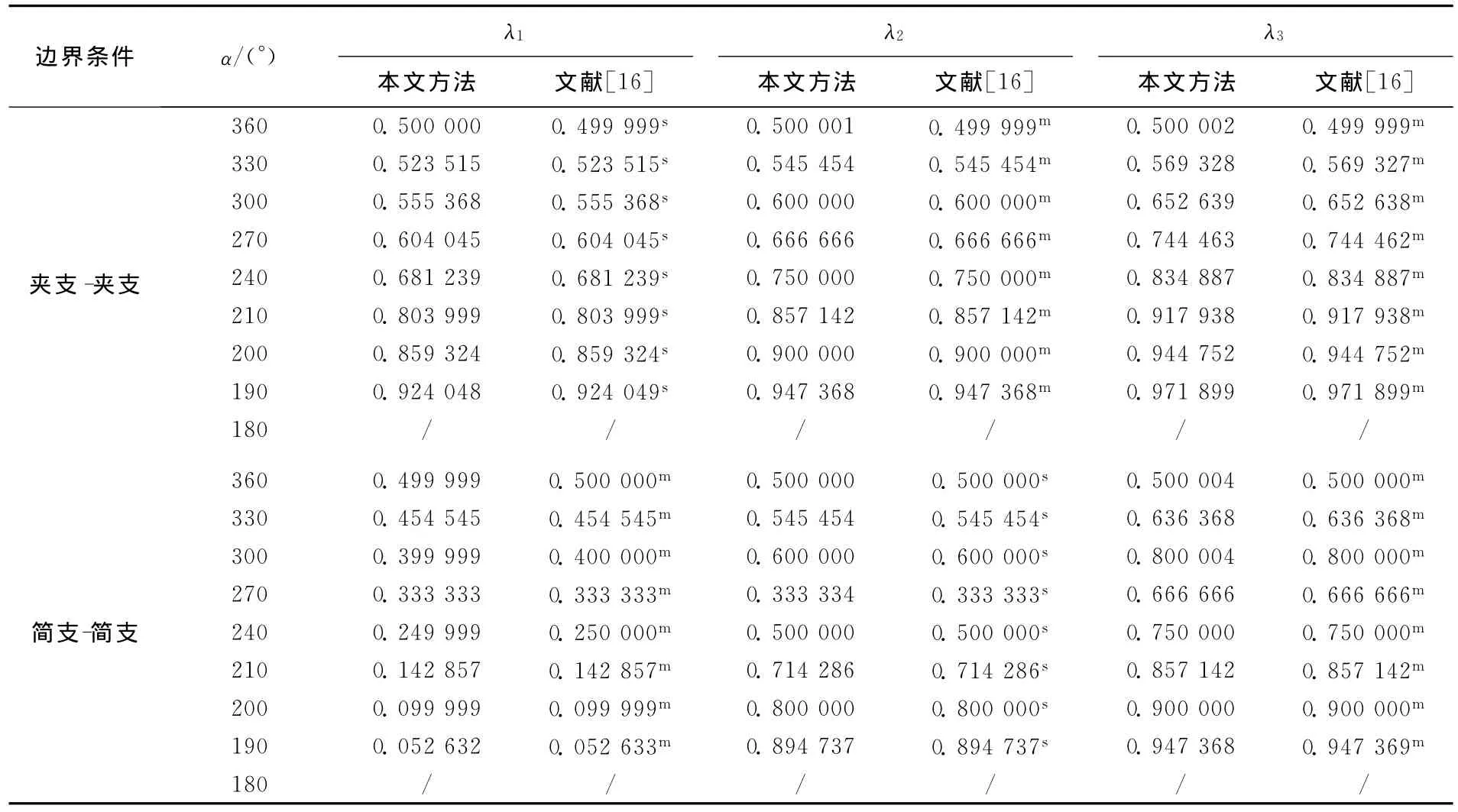
表2 夹支－夹支和简支－简支边界条件下的切口应力奇性指数

4 结束语

本文根据线弹性理论及切口尖端位移场的级数渐近展开假设，推导出了关于功能梯度中厚板切口尖端奇性指数的特征微分方程组。推导发现，采用Reissner假设的功能梯度板切口的奇性与板厚度方向材料的弹性模量变化无关。本文所提方法能一次计算出板切口的各阶奇性指数，克服了传统方法迭代求解超越方程的不足，所求出的矩奇异和剪切奇异可由相应的特征角函数区分。研究表明，若采用薄板理论，功能梯度板切口的奇异性与板厚方向材料的弹性模量有关，功能梯度薄板切口奇异性研究将是进一步的工作。

［1］ Nguyen T K，Sab K，Bonnet G.First－order shear deformation plate models for functionally graded materials［J］.Compos Struct，2008，83（1）：25－36.

［2］ 王 强，程长征，张长会.几何特征对含切口构件疲劳寿命的影响［J］.合肥工业大学学报：自然科学版，2013，36（3）：327－331.

［3］ Filippi S，Lazzarin P，Tovo R.Developments of some explicit formulas useful to describe elastic stress fields ahead of notches in plates ［J］.Int J Solids Struct，2002，39（17）：4543－4565.

［4］ Kotousov A.Effect of plate thickness on stress state at sharp notches and the strength paradox of thick plates［J］.Int J Solids Struct，2010，47（14）：1916－1923.

［5］ Carpinteri A，Paggi M.On the asymptotic stress field in angularly nonhomogeneous materials ［J］.Int J Fracture，2005，135（1／2／3／4）：267－283.

［6］ Linkov A，Rusinek L R.Evaluation of stress concentration in multi－wedge systems with functionally graded wedges［J］.Int J Eng Sci，2012，61：87－93.

［7］ Carpinteri A，Pugno N.Cracks and re－entrant corners in functionally graded materials［J］.Eng Fract Mech，2006，73（10）：1279－1291.

［8］ Mehran S，Rouhi S，Ramzani B，et al.Fracture analysis of functionally graded materials with U－and V－notches under mode I loading using the averaged strain－energy density criterion［J］.Fatigue Fract Engng Mater Struct，2011，35（7）：614－627.

［9］ Kubair D V.Stress concentration factor in functionally graded plates with circular holes subjected to anti－plane shear loading［J］.J Elast，2014，114（2）：179－196.

［10］ Barati E，Alizadeh Y.A numerical method for evaluation of J－integral in plates made of functionally graded materials with sharp and blunt V－notches［J］.Fatigue Fract Engng Mater Struct，2011，34（12）：1041－1052.

［11］ Saidi A R，Hejripour F，Jomehzadeh E.On the stress singularities and boundary layer in moderately thick functionally graded sectorial plates［J］.Appl Math Model，2010，34（11）：3478－3492.

［12］ Huang C S，Chang M J.Corner stress singularities in an FGM thin plate［J］.Int J Solids Struct，2007，44（9）：2802－2819.

［13］ Huang C S.Corner stress singularities in a high－order plate theory［J］.Comput Struct，2004，82（20）：1657－1669.

［14］ Huang C S，Chang M J.Geometrically induced stress singularities of a thick FGM plate based on the third－order shear deformation theory［J］.Mech Advanced Mater Struct，2009，16（2）：83－97.

［15］ Niu Z R，Ge D L，Cheng C Z，et al.Evaluation of the stress singularities of plane V－notches in bonded dissimilar materials［J］.Appl Math Model，2009，33（3）：1776－1792.

［16］ Huang C S.Stress singularities at angular corners in firstorder shear deformation plate theory［J］.Mech Sci，2003，45（1）：1－20.