基于KED法的夹轨装置动态特性研究

柳 波， 彭志方， 龙紫照，2

（1.中南大学 机电工程学院，湖南 长沙 410012；2.湘电集团有限公司，湖南 湘潭 411101）

轮轨式扒渣机主要用于安装有轨道的巷道、隧洞中，是一种用于连续装载块状固料（如石渣、煤炭）的理想设备。夹轨装置作为轮轨式扒渣机系统总成的重要部分，主要功能是防止车体产生相对滑动，同时降低车体受冲击和振动的影响。夹轨装置在受到外载荷的作用下，杆件表现出柔性，产生弹性变形，变形会对构件的夹持精度和夹持稳定性产生很大影响。以往对夹轨装置的研究都将机构视为刚体［1］，得出的分析结果与实际情况误差较大，因此，为了得到更为真实的结果，必须采用弹性动力学的方法对夹轨装置进行研究。

目前，人们在研究机构弹性动力学建模方面取得了一定的成就。文献［2－3］建立了集中参数模型，该方法建立的运动方程求解方便，但所建模型精度不高；文献［4］最早运用表示单元梁横向位移函数的五次埃尔米特插值函数法对系统阵型曲线进行精确模拟，从中得到了单元的最大应力值及其位置；在此基础上文献［5］总结并推导出一套针对平面连杆机构的弹性动力学分析方法。

由于夹轨装置处于不同夹紧位型和不同安装位置时，夹轨装置所表现出的柔性、滞后性会有所不同，因此，本文采用弹性动力学方法，对夹持装置在不同夹紧位型和不同安装位置时的动态特性进行分析，以找到更合理的夹紧位型和安装位置，提高夹轨装置夹持的有效性和稳定性。

1 系统弹性动力学建模

采用 KED（kineto－elastic－dynamics）法以简化分析过程，使分析结果更加准确。

1.1 梁单元位型函数的建立

为方便求解，采用基于梁单元理论的有限元模型［6］，进行复杂结构的分析。等截面梁单元如图1所示，其中，u1、u5为横向位移；u2、u6为纵向位移；u3、u7为弹性转角；u4、u8为曲率。

图1 等截面梁单元

对整个单元的位移分布进行假定，由于夹轨装置振动时机构的动态变形复杂，因此在分析梁的横向位移时需要运用次数较高的五次埃尔米特差值多项式［7］法，提高模型的计算精度。梁横向位移的五次埃尔米特多项式分布为：

纵向位移假设为线性分布，即

（1）式和（2）式中共有8个未知系数，要得出这些系数的值，需要在节点A、B处建立8个广义坐标［6］，然后以节点处的广义坐标为未知量推导单元的运动方程。单元广义坐标列阵由8个广义坐标构成，即

1.2 单元动力学方程的建立

通过计算单元的动能及变形能可得到单元的等效质量矩阵和等效刚度矩阵［8］，将等效质量矩阵和等效刚度矩阵代入拉格朗日方程可以得到单元的动力学方程，其矩阵形式如（4）式所示，具体的推导过程参见文献［8］。

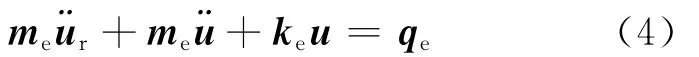
其中，me为单元的质量矩阵；ke为刚度矩阵；qe为外力与单元的作用力列阵；u为广义坐标列阵；为广义加速度列阵；为刚体单元的加速度列阵为弯曲变形的角加速度值在 构件考虑成刚体时值为0。

1.3 系统运动微分方程的总装配

由第i（i＝0，1，…）单元坐标系与系统坐标系

的关系［8］，可得当量质量矩阵和当量刚度矩阵，其中Ri为坐标转换矩阵，进一步可以得到第i单元的运动微分方程为［8］：

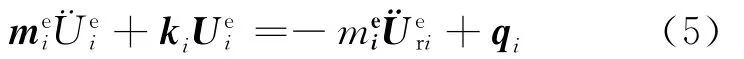
系统与单元坐标系的关系［8］可表达为：

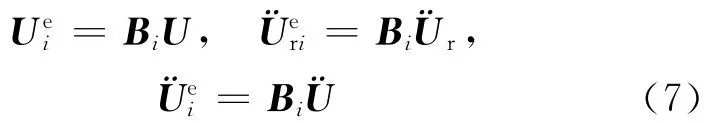
其中，Bi为坐标协调矩阵；为整体坐标系中的刚体加速度列阵。将（7）式代入（5）式，可得到系统运动微分方程为：

其中，K、M分别为系统的刚度矩阵以及质量矩阵；Q为广义力列阵。M、K、Q计算公式为：

（8）式即弹性动力学方程，修改不同的系数矩阵即可对夹轨装置的不同夹紧位型和安装位置进行动力学响应特性分析。

2 夹轨装置弹性动力学建模

夹轨装置结构及夹紧工况如图2所示。

图2 夹轨装置结构及夹紧工况图

夹轨装置在工作中，通过油缸的伸缩，控制钳臂的开合，实现对轨道的夹紧与松开。在夹紧的过程中，结合活动夹块的限位摆动，实现自动找中，并通过左、右活动夹块的凹槽面实现对轨道的夹紧。夹轨装置的几何尺寸见表1所列。

表1 夹轨装置几何尺寸 mm

根据夹轨装置的结构特点，建立装置的动力学模型，如图3所示。在分析过程中，将油缸视为阶梯轴，利用文献［9］中公式进行处理，可得：

其中，I为惯性矩；E为弹性模量。

处理后的油缸被视为等截面梁，将此梁分成2个单元，钳臂被分成3个单元。系统的单元编号分别用1，2，3，…表示；U1，U2，…表示系统的广义坐标；A、B、C、A′、B′、C′表示关键铰链节点。

夹轨装置系统由8个单元、7个节点和26个广义坐标构成，表达成一个8×8的矩阵Iu［8］为：

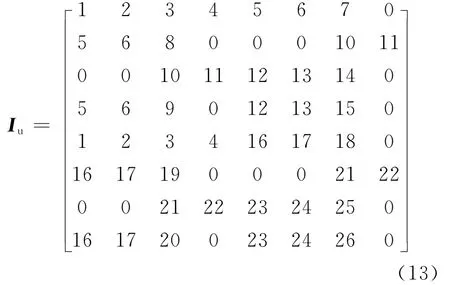
图3 夹轨装置动力学模型

坐标协调矩阵Bi是用来联系单元坐标系与广义坐标系的关系矩阵，该矩阵的维数为8×N，矩阵全部由0或1组成，模型组成矩阵中的行元素与系统单元的广义坐标对应，模型组成矩阵行元素中非0值决定协调矩阵中对应取值为1的元素，模型组成矩阵的非0值的列数决定协调矩阵的行数，其余不是1的都取值为0。所以根据模型矩阵的定义可以得出系统各坐标协调矩阵，如（14）式的B1、（15）式的B2，同理可得B3、B4、B5、B6、B7、B8。

坐标转换矩阵R［8］的表达式为：

其中，θ为梁单元与x轴正方向的夹角。

根据坐标转换矩阵及模型矩阵可以得到单元的坐标转换矩阵，如（17）式的R1、（18）式的R2，同理可得R3、R4、R5、R6、R7、R8。

3 夹轨装置动态特性分析

3.1 不同夹紧位型下夹轨装置弹性位移响应

油缸伸长量的不同，改变了夹轨装置的夹紧位型，导致系统的刚度矩阵发生变化，进而影响机构的弹性位移响应。因此，必须采用Newmark－β法［10］编写程序，对不同油缸伸长量下夹轨装置各重要节点进行运算，找出关键节点的弹性位移响应规律，得到最恰当的夹紧位型。

在已建立的模型中，由于油缸铰点U5及钳臂铰点U10为机构的关键节点，运动副节点U12、U13决定了夹轨装置能否实现可靠夹持，因此选择这几个点进行分析。分析中工作装置的作业工况为纵向挖掘，关键节点弹性位移如图4所示。

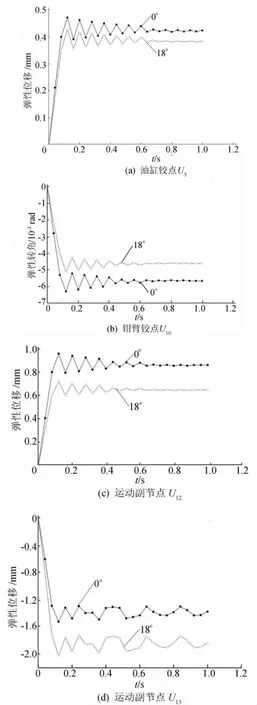
图4 不同夹紧位型关键节点弹性位移

由图4可知，当开口角度为0°时，油缸铰点弹性位移U5、钳臂铰点弹性转角U10以及钳口铰点横向弹性位移U12的数值明显大于开口角度为18°时的值，而钳口铰点竖直弹性位移U13则小于18°角的夹紧状态。其中当张开角度为0°时，U12弹性位移最大值达到0.96mm，而18°角时U12弹性位移最大值达到0.72mm。分析结果显示，开口角度为18°时夹轨装置稳定性明显高于0°时，为最佳的夹紧位型。

3.2 不同安装位置时夹轨装置弹性位移响应

夹轨装置处于不同安装位置即改变了KED法中的广义力列阵，其所受外力及倾翻力矩会发生变化，导致夹轨装置的夹持性能发生改变。为了提高扒渣机夹轨装置的夹持性能，防止扒渣机出现倾翻等危险情况，必须对处于不同安装位置下的夹轨装置进行弹性位移响应分析，从而确立合理的安装位置。通常夹轨装置的安装位置多位于前行走轮前、后，因此主要针对前行走轮前、后位置即距离后行走轮1 710mm和1 150mm 2个位置，分析其关键节点位移计算值，如图5所示。

图5 不同安装位置关键节点弹性位移

由图5可知，安装位置的不同对于夹轨装置各节点的弹性位移有一定的影响，其中对节点U13的影响最大。从U13的分析中可以看出离倾翻线即后行走轮距离越远，则节点的弹性位移值越小，这是因为距后行走轮距离越远，夹轨装置的力臂越长，受倾翻力矩和外力的影响越小。因此，在进行安装位置的选择时，并考虑底盘结构的前提下，必须尽量将夹轨装置安装于车体前部，以减小作业过程中夹轨装置所受的倾翻力。

4 结束语

本文以KED法为依据，建立了轮轨式扒渣机夹轨装置的弹性动力学模型。利用数值积分法Newmark－β法编写Matlab程序计算夹轨装置不同夹紧位型、不同安装位置下机构的关键节点的弹性位移值，得出夹轨装置最为合理的夹紧位型和安装位置。

［1］ 黎压飞，邱清盈，冯培恩.基于刚柔混合建模的时变结构动力学分 析 ［J］.浙 江 大 学 学 报：工 学 版，2007，41（2）：311－314.

［2］ Bagci C，Kurnool S.Exact response analysis and dynamic design of cam－follower systems using Laplace transforms［J］.Journal of Mechanical Design，1997，119（3）：359－369.

［3］ Erdman A G，Sandor G N，Oakberg R G.A general method for kineto－elastodynamic analysis and synthesis of mechanisms［J］.Journal of Engineering for Industry，1972，94（4）：1193－1205.

［4］ Nath P K，Ghosh A.Kineto－elastodynamic analysis of mechanisms by finite element method［J］.Mechanism and Machine Theory，1980，15（3）：179－197.

［5］ 高 峰，黄 真.空间机构摆动力完全平衡最少条件数和并联机器人机构的摆动力平衡［J］.机械设计，1992，9（1）：29－31.

［6］ 刘 艳，柳炳康，王 琦.梁端水平加腋与塑性铰关系的非线性有限元分析［J］.合肥工业大学学报：自然科学版，2004，27（7）：742－746.

［7］ 王生泽，廖道训.平面连杆机构梁单元的横向位移函数及长度划分［J］.华中理工大学学报：自然科学版，1988，16（3）：107－113.

［8］ 张 策.弹性连杆机构的分析与设计［M］.第2版.北京：机械工业出版社，1997：60－120.

［9］ 吴亚平.变截面压杆稳定性计算的等效刚度法［J］.力学与实践，1994，16（1）：58－60.

［10］ 王焕定，马 赫，曾 森.结构动力学逐步积分算法稳定性讨论 ［J］.哈 尔 滨 工 业 大 学 学 报，2008，40（10）：1513－1516.