FSAE赛车操纵稳定性虚拟仿真与实车试验研究

邓召文， 徐成强， 王保华

（湖北汽车工业学院 汽车工程学院，湖北 十堰 442002）

大学生方程式汽车大赛（FSAE）是一项由国际汽车工程师学会举办的面向大学生的综合性工程教育赛事。在FSAE赛车悬架系统的优化设计中，借助多刚体动力学ADAMS软件进行悬架运动学分析逐渐成为一种常用手段［1］。利用ADAMS软件对前轮定位参数进行多目标优化设计仍然是困扰设计者的难题，文献［1－2］曾尝试对此问题做过研究。在国外，悬架数据采集系统已经被广泛地运用在FSAE赛车上，而国内应用较少，其中文献［3］开发的赛车数据采集系统可以采集发动机转速、横向加速度等信号，适用于赛车的实时监控。

在FSAE赛车的设计中，由于对赛车的操作稳定性要求很高，一般采用不等长双横臂独立悬架，如图1所示。不等长双横臂独立悬架具有结构简单、轻便可靠和性能优异等优点［4］。本文以FSAE赛车为研究对象，重点研究赛车虚拟样机整车模型的建立与准确性验证；通过分析整车仿真数据来评价赛车的转向、抗侧倾和抗侧滑等方面的性能；通过对比分析蛇形穿越实车试验与虚拟仿真试验数据曲线，对整车调校和车手驾驶习惯的校正提出了一些建议。

图1 某赛车悬架系统的CAD模型

1 FSAE赛车虚拟样机整车模型

1.1 虚拟样机模型的建立

本文基于ADAMS／Car模块建立了完整的FSAE赛车模型，包括前悬架子系统、转向子系统、后悬架子系统、动力总成子系统、轮胎子系统及车身子系统等。在建模过程中，首先对整车系统进行分解及动力学抽象，构建出相对于各子系统的拓扑图，研究这些拓扑结构并搭建通讯器；然后，对各子系统的物理、几何和力学等参数进行获取，并定义好各子系统相应的参数；最后，建立装配文件，构建出整车的动力学模型［5］。

对FSAE赛车的整车模型进行硬点坐标赋值和参数定义，可以得到某赛车的仿真模型。初始硬点坐标值均在建立的CATIA线框模型中测得；基于ADAMS／Car模块分别对前、后悬架进行仿真分析，得到设计变量和优化目标；基于ADAMS／Insight模块，对悬架进行多目标优化设计，使优化目标达到设计要求，最终得到用于实车制造的硬点坐标值。

为了使仿真得到的结果更加准确，编制了重要部件的属性文件：弹簧和减振器的特性曲线参数均根据生产厂家提供的数据编制；前、后轮胎模型属性文件分别根据轮胎测试联盟提供的Hoosier 20.5×7R13和 Hoosier 20.0×7.5R13轮胎数据编制。

按照上述整车模型建立方法，构建出本文所研究的某赛车整车模型，如图2所示。

图2 某赛车的整车仿真模型

为了简化模型的建立，本文中的赛车模型采用了大量的属性文件替代实体文件［6］。例如，动力系统是将发动机的外特性曲线编辑成动力模块的属性文件，并直接将动力通过函数和数据来驱动整车的运动。

1.2 虚拟稳态回转仿真试验的模型准确性验证

虚拟稳态回转仿真试验，亦称为定半径转向实验，是整车仿真分析中一种典型的实验手段，通过使用驱动器来开环或闭环地控制车辆的转向、制动、油门开度和变速器等参数，并使汽车按照仿真条件行驶在模拟的圆形车道上。该实验主要用于分析和评估汽车的操作稳定性和动态响应特性，也可用于验证仿真模型的准确性［7］。

为了评价FSAE赛车的转向特性、侧倾和横向加速度特性，根据文献［8］的要求，本次稳态回转实验采用的是固定方向盘转向角法。由于此次实验是模拟FSAE动态项目中的8字绕环，因此模拟赛道的参数设置需与实际基本相同。8字绕环赛道如图3所示。

图3 8字绕环赛道示意图

根据8字绕环的赛道规则，赛道内侧直径为15.25m，赛道宽为3.0m，假设赛车正好行驶在赛道的中间，则行驶半径为9.125m，行驶路径长为57.305m。

假设赛车匀速完成8字绕环的单圈时间为6s，则赛车行驶的平均速度为9.55m／s，将此速度设定为仿真条件，通过比较理论和仿真的单圈时间来检验ADAMS整车模型的准确性。由于每进行1圈仿真，重心的横向位移就会归零1次，因此将其作为标记。经过仿真，得到重心横向位移与时间的变化关系曲线，如图4所示。

由图4可以看出，完成5次8字绕环的时间大约为30s，即每次用时大约为6s，与理论值几乎一致，说明该模型的准确性很高，为下一步进行整车操控稳定性仿真试验奠定了基础。

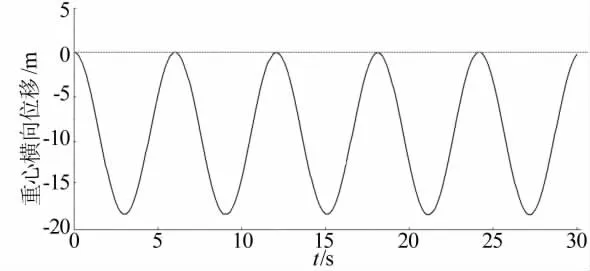
图4 重心横向位移与时间的关系曲线

2 整车虚拟仿真

整车虚拟仿真是指在ADAMS／Car模块中使用完整的赛车模型进行各种动力学仿真分析，实验基于与真实路面相似的模拟路面，使用驱动器来控制仿真的整车模型。使用此分析方法，可以对整车的虚拟原型进行一系列的平顺性、操纵稳定性和动力学仿真分析，从而得到各种需要的特性曲线和仿真动画。本文将基于某赛车的整车模型进行仿真分析，目的在于检验前、后悬架的侧倾角刚度匹配是否合理，以及赛车在极限弯道工况下的整车操纵稳定性。

2.1 虚拟稳态回转仿真试验

传统型汽车为了使转向更稳定，需要有适度的不足转向；但由于FSAE赛车必须具有出色的弯道性能才能在布满各种障碍的赛道上取得较好的成绩，因此转向特性一般被设计为中性。由于实际很难达到理想的中性转向特性，所以FSAE赛车的转向特性一般都会被设计成极微不足或极微过度转向，具体的偏好特性取决于车手的驾驶能力与风格。由于FSAE赛车是由大学生驾驶，无论在驾驭能力还是技术水平方面，相对于专业赛车手都存在巨大差距。为了获得良好的弯道性能和易操控性，大多数FSAE赛车的转向特性都被设定为极微不足转向［9］。本次的虚拟稳态回转仿真试验主要是检验某赛车的转向特性是否符合极微不足转向的设计要求。

由于FSAE赛车与乘用车区别很大，因此本文的稳态实验条件是专门针对FSAE赛车定制的。这导致无法使用ADAMS软件中标准的实验模块，所以需要单独编写仿真工况（Event Builder），该工况由3个子工况构成。

（1）初始的稳定车速设定为5km／h，调整方向盘的转角，最终实验的转弯半径为9.125m。

（2）当赛车绕赛道稳定回转1圈之后，固定方向盘转角。

（3）按照工况（2）中的稳态回转赛道缓慢加速到30km／h，停止实验，记录整个仿真过程。赛车的转弯半径随车速变化的仿真曲线，如图5所示。

定义R0为初始的转弯半径，Ri为第i点的转弯半径，如果Ri／R0＞1（即转弯半径随车速的增大而增大），则为不足转向；如果Ri／R0＜1（即转弯半径随车速的增加而减小），则为过度转向。

图5 转弯半径随车速变化的仿真曲线

由图5可以看出，当方向盘的转角固定之后，赛车的转弯半径随着车速的增大而增大。车速从14km／h变为30km／h的过程中，转弯半径随之由9.09m逐渐增大到9.69m，增加量为0.6m，表明某赛车具有极轻微的不足转向特性，验证了赛车的转向系统符合设计要求。

2.2 虚拟蛇形穿越仿真试验

蛇形穿越仿真是一种检验汽车瞬态响应特性的重要实验手段，在急转向侧翻工况下，仿真分析横摆角速度、侧向加速度、方向盘转角和侧偏角等汽车行驶性能参数。通过查看这些参数判断汽车在极限工况下是否还能处于良好的操控范围内［10］。

蛇形穿越的路径设置如图6所示，参照文献［8］，被评价的汽车在规定的道路上进行高速绕桩，反复在虚拟直线附近做蛇形穿越试验，期间不能碰到标杆，也不能出现翻车的情况，以此作为评价极限状态下汽车的抗弯能力。该试验对驾驶员的驾驶方法不做任何特殊规定，以顺利穿桩为准，因此，它属于闭环试验［11］。

图6 蛇形穿越实验路径示意图

由于本次实验是专门针对FSAE赛车定制的，ADAMS的标准模板无法提供所需的行驶路径和驾驶员驱动文件，故需要单独编写此仿真工况。参照FSAE赛事的蛇形穿越规则，设定标桩的间距为9m。某赛车宽为1.4m，结合车手的驾驶经验，设定路径的最大横向位移为1.3m，最终得到赛车的行驶路径，如图7所示。

图7 FSAE赛车的蛇形穿越实验路径

实际的蛇形穿越试验是指汽车在虚拟直线两侧多次变速穿越行驶，而在ADAMS中，为了简化实验，大多将速度设为恒定，通过多组实验的方法来检验汽车抗弯能力。因此，本文有针对性地设定4次实验的车速分别为10、11、12、13m／s。仿真时，首先让赛车直线行驶，待达到预定车速稳定行驶后，再按设定的路径进行实验。仿真结束后分别得到赛车的车架侧倾角、横摆角速度和侧向加速度随纵向位移的变化曲线，如图8所示。

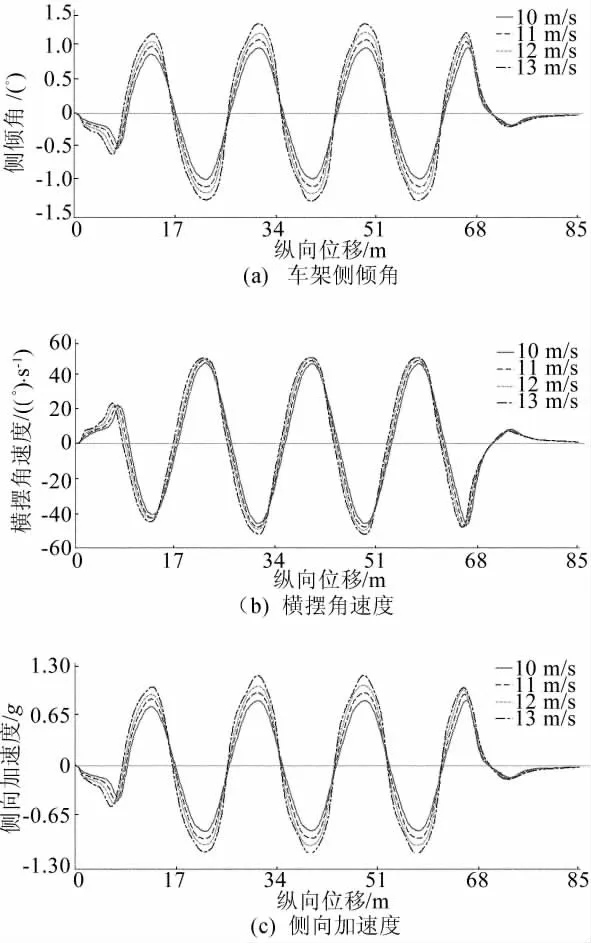
图8 赛车车架侧倾角、横摆角速度和侧向加速度随纵向位移的变化曲线

由图8可知，车架外倾角会随着车速的增大而增大，但最大值仍不超过1.3°，说明赛车的侧倾角刚度较大，抗侧倾能力较强；车速的增大会导致赛车的横摆角速度随之增大，但增幅很小，说明赛车的转向准确性较高，这可以增加驾驶员在转向时的信心；赛车的侧向加速度会随着车速的增大而增大，且与车架外倾角的变化趋势相同，本组实验中的极限侧向加速度在1.15g左右，说明赛车的侧向支撑能力较好，且抗侧滑能力也较强。

3 实车试验分析

由于实际加工与装配过程中可能存在误差，导致某赛车的各种参数与理论值发生偏差，从而影响赛车的性能。因此，本文引入了悬架数据采集系统对实车进行试验，通过与理论值进行对比分析，验证整车的操控性是否满足设计要求。

3.1 悬架数据采集系统

悬架数据采集系统是指将传感器采集的信号通过一系列的处理，最终在电脑端实现实时监测整车的相关性能参数［12］。虚拟样机和虚拟仪器联合应用，能更好地将实车试验和仿真试验结合起来，提高赛车的操控稳定性和技术含量［13］。

利用该系统对赛车前、后悬架系统的减振器行程和车轮行程进行数据采集，并基于LabView软件对数据进行后处理，最终得到减振器位移和车轮载荷等实时显示的信息。通过安装在赛车上的4根直线位移传感器和数据采集系统，借助无线传输模块，最终在电脑端得到所需数据的实时显示。

3.2 基于悬架数据采集系统的实车试验分析

为了综合评价某赛车的操控性，借助悬架数据采集系统采集实车数据，通过分析该数据来验证和调校赛车的操控性。选取2.2节中介绍的虚拟蛇形穿越仿真试验作为实车试验的测试工况。

为了与理论值进行对比，蛇形穿越实车试验与仿真试验的条件设置相同，但由于实际路面条件的限制，只能选取水泥路面进行试验，为了保证赛车在可控范围内，设置仿真和试验的车速均为10m／s。ADAMS仿真和实车试验得到的减振器行程随时间的变化关系，如图9所示。

对比分析图9a和图9b，可得出以下结论：

（1）为了便于数据显示，图9b中只截取了部分蛇形穿越试验的数据。由图9b可以看出，试验大致进行了2个周期（定义顺利穿过2个标杆为1个周期），耗时为4.3s；而从图9a中可以看出，完成2个周期用时为3.8s，实际测试要比理论值慢0.5s，说明实际测试过程中车手在第1个周期有减速的动作，此结果可用于指导车手改良自己的驾驶习惯。

（2）由图9a可以看出，前、后悬架的静平衡位置分别为200、198mm，相对减振器的自由行程（215mm）分别压缩了15、17mm，与图9b中的前、后减振器压缩量波动中心值（即实车静平衡位置）大致相同，说明经过悬架刚度标定后，实车弹簧刚度恰好满足设计要求。

（3）由图9a可以看出，蛇形穿越实验中，前、后悬架的减振器压缩量分别为12、8mm；由图9b可以看出，实际试验中，前、后悬架的减振器压缩量分别为12.5、11.0mm。对比2组数据，发现实测的前悬侧倾角与理论值基本相同，而后悬侧倾角相对理论值偏大，说明后悬架的侧倾角刚度不足，但由于已校核过弹簧刚度，因此，导致后悬架侧倾角刚度偏小的原因可能是后稳定杆刚度不足。由于此类情况会增加赛车的不足转向特性，导致赛车的弯道性能变差，因此需要增加后稳定杆的侧倾角刚度。在相同工况下，仿真和试验的减振器压缩量大致相同，表明悬架系统的传力机构工作正常，且说明赛车的抗侧倾能力与理论值相符，符合赛车的设计要求。

图9 仿真和实车试验得到的减振器行程随时间的变化关系

4 结 论

（1）建立FSAE赛车的整车仿真模型，并对其进行硬点坐标赋值和参数定义，最终得到了某赛车的仿真模型。设置与实际相同条件的虚拟稳态回转仿真试验，通过对比仿真和实际的8字绕环成绩，验证了整车模型具有较高的准确性。

（2）进行了虚拟稳态回转仿真试验，当固定方向盘转角后，随着车速的缓慢增大，转弯半径从9.09m逐渐增大到9.69m，表明某赛车具有极轻微的不足转向特性，符合设计要求。

（3）在虚拟蛇形穿越仿真试验中，参考FSAE赛事规则进行条件设置，并通过多组实验最终得到车架侧倾角的最大值仍不超过1.3°，证明整车侧倾角刚度足够大；侧向加速度在1.15g时仍未出现侧滑现象，表明赛车的侧向支撑能力较好，抗侧滑能力也较强。

（4）借助某赛车的悬架数据采集系统，进行了蛇形穿越试验，通过对比分析仿真和试验数据，发现后稳定刚度不足导致赛车的转向不足程度增加，需要调节。开发的悬架数据采集系统能实时监测赛车悬架的工作状态，对指导整车的设计和调校均有较大帮助。

［1］ 倪 俊，徐 彬.FSAE赛车双横臂前悬架运动学仿真及优化［J］.车辆与动力技术，2011（4）：53－56.

［2］ 王 行，阳 林，彭仁杰，等.基于ADAMS的FSAE赛车前悬架优化设计［J］.广东工业大学学报，2013，30（3）：105－108.

［3］ 董瑞佳，汪国民.基于Labview的FSAE赛车动态性能测试系统［J］.工业控制计算机，2011，24（7）：8－9.

［4］ 刘 涛.汽车设计［M］.北京：北京大学出版社，2008：57－62.

［5］ 陈 军.MSC.ADAMS技术与工程分析实例［M］.北京：中国水利水电出版社，2008：265－270.

［6］ 倪 俊，徐 彬.基于ADAMS的FSAE赛车建模与操纵稳定性仿真［J］.工程设计学报，2011（5）：40－44.

［7］ Milliken W F，Milliken D L.Race car vehicle dynamics［M］.Society of Automobile Engineers Inc，1995：677－682.

［8］ GB／T 6323.6－1994，汽车操纵稳定性试验方法稳态回转试验［S］.

［9］ 向铁明，周水庭.FSC赛车转向梯形机构断开点仿真与优化设计［J］.宁夏大学学报：自然科学版，2013（3）：238－241.

［10］ 柴 天.FSAE赛车整车性能分析与研究［D］.长沙：湖南大学，2009.

［11］ 张 武.FSAE赛车操控稳定性的仿真［D］.长沙：湖南大学，2008.

［12］ LaChausse J，Doll R.Implementation of a stand－alone date acquisition system for a formula SAE racing car［R］.Rochester：Rochester Institute of Technology，2005.

［13］ 刘 虹，王其东.基于ADAMS双横臂独立悬架的运动学仿真分析［J］.合肥工业大学学报：自然科学版，2007，30（1）：57－59.