重载下准双曲面齿轮传动界面润滑机理分析

蒲伟,王家序,2,杨荣松,朱东,周广武,吴继强

(1.四川大学空天科学与工程学院,610065,成都;2.重庆大学机械传动国家重点实验室,400044,重庆)



重载下准双曲面齿轮传动界面润滑机理分析

蒲伟1,王家序1,2,杨荣松1,朱东1,周广武1,吴继强1

(1.四川大学空天科学与工程学院,610065,成都;2.重庆大学机械传动国家重点实验室,400044,重庆)

综合考虑了准双曲面齿轮传动接触几何、卷吸速度与椭圆主轴不重合、润滑剂流变特性等因素,建立了准双曲面齿轮传动界面润滑机理分析的统一数学模型,数值分析了重载下准双曲面齿轮传动一对啮合副从啮入到啮出过程中啮合点油膜、压力、闪温和von Mises应力的演变规律,探讨了小齿轮转速对传动界面润滑性能的影响。结果表明:从啮入到啮出过程中,啮合点的中心油膜厚度和最大von Mises应力呈现单调递减趋势,表面最大闪温则是先升高然后逐渐降低;转速对传动界面润滑状态的影响非常显著,随着转速的逐渐减小,啮合点中心油膜厚度也随之减小,由于工程中粗糙表面的存在,界面容易因滑动摩擦发生磨损;转速越高,啮合点的闪温也越高,此时齿面容易发生胶合失效,为了最大限度地避免齿面磨损和胶合,需要合理选择准双曲面齿轮的运行转速。

准双曲面齿轮;重载;闪温;von Mises应力

准双曲面齿轮具有能传递相交轴运动和动力、传动平稳、承载能力强等优点,是航空发动机、直升机、重载卡车等装备传动系统中的关键基础零部件,其性能直接决定着整个装备的工作性能和服役寿命。由于准双曲面齿轮传动的几何特性、啮合方式以及加工调整都远比渐开线齿轮的复杂,在服役过程中,其轮齿界面容易因润滑不良诱发点蚀、胶合、磨损、裂纹等齿面失效,因此,深入研究此类传动的润滑机理,对改善和提高我国直升机、重载卡车等典型装备中准双曲面齿轮传动的综合性能具有十分重要的意义[1]。

最早的齿轮润滑研究可以追溯到1916年Martin的工作[2],当时轮齿被简化成理想光滑的刚性体,导致计算结果与工程实际情况相差甚远。20世纪50年代以后迅速发展起来的弹性流体动力润滑理论,考虑了界面处弹性变形和润滑油黏度增加的影响,使得油膜厚度的预测值与试验值十分吻合,从而为齿轮润滑研究奠定了坚实的基础[3]。在近年界面研究取得的突破性进展的基础上,人们开始了对圆柱齿轮混合润滑的研究。例如,Zhu等人运用最新的真实三维粗糙表面线接触混合润滑模型和表面以下应力场的快速计算法,将Ioannides-Harris-Zaretsky疲劳寿命模型引入齿轮疲劳寿命预测中,形成了齿轮接触疲劳寿命预测的新模型,并对15组齿轮进行了疲劳寿命预测,结果与大量齿轮寿命试验数据相当一致[4]。目前针对准双曲面齿轮传动弹流润滑的分析相对较少,具有代表性的如Simon和Chao等人的工作[5-6]。由于准双曲面齿轮传动的卷吸速度方向与椭圆短轴成一夹角,导致其润滑分析更为复杂,而对于重载情况,此前尚无行之有效的分析方法[1]。以往的研究大多在轻中载、光滑表面、厚油膜情况下进行,并没有考虑重载润滑的情况。此外,在准双曲面齿轮闪温、摩擦分析等方面,近年也有研究者从不同的角度进行了有益的探索,例如:谷建功等人在Blok公式的基础上改进了准双曲面齿轮传动闪温的计算方法[7];苏华等人对准双曲面齿轮的热摩擦学进行了探索,提出了基于有限元法的热接触分析和传热计算模型[8]。但是,这些研究在界面机理分析方面采用了各种各样的简化处理,忽略了润滑油膜的影响。到目前为止,尚未发现有关于准双曲面齿轮完整的基于润滑分析的轮齿界面闪温、下表面应力分布方面的研究成果。

有鉴于此,本文在作者近期取得针对卷吸速度方向与椭圆短轴成一夹角的重载薄膜润滑完全数值解法[1,9]的基础上,综合考虑准双曲面齿轮传动的啮合几何、卷吸速度大小和夹角、润滑剂流变特性、载荷分配等因素,建立准双曲面齿轮传动的润滑模型,全面深入地研究此类传动在重载工况下轮齿接触界面的油膜压力、闪温以及下表面应力随小齿轮转速的变化规律,以期为揭示准双曲面齿轮传动的润滑机理以及性能优化提供理论依据,并为进一步考虑真实轮齿粗糙表面的准双曲面齿轮传动混合润滑分析奠定基础。

1 啮合模型

研究准双曲面齿轮传动的润滑特性,首先需要建立准双曲面齿轮传动的三维啮合模型,求解出传动界面啮合点的接触几何以及相对啮合点的运动参数。目前,关于准双曲面齿轮传动的啮合几何分析方法[10-11]已比较成熟,但在此做一简明扼要的阐述仍有必要。

准双曲面齿轮传动的安装位置关系如图1所示,其中pr是从大齿轮大端到小端轴线方向的单位矢量,pl是从小齿轮大端到小端轴线方向的单位矢量,e是pr和pl公垂线的单位矢量。

图1 准双曲面齿轮运动的几何关系

考虑到大、小齿轮回转方向相反,啮合点处齿面的相对运动速度V12、卷吸速度V1+2按下式计算

(1)

式中:ω1为小齿轮转速;n为小齿轮齿数;N为大齿轮齿数。

准双曲面齿轮传动接触的几何关系如图2所示。根据文献[10]中的准双曲面齿轮传动齿面接触分析,可以求出小齿轮齿面和大齿轮齿面在相互垂直方向x1和y1的法曲率K1x1、K1y1、K2x1、K2y1及扭曲率G1、G2,此外,还可以求得瞬时接触椭圆长轴方向和x轴的夹角τ,以及椭圆长轴的长度和方向矢量u。

图2 准双曲面齿轮传动接触的几何关系

根据x1和y1的法曲率K1x1、K1y1、K2x1、K2y1及扭曲率G1、G2,由曲率计算公式,可以按方程组(2)求得瞬时接触椭圆长轴方向u和短轴方向v的小齿轮轮齿法曲率面K1u和K1v,以及大齿轮轮齿法曲率面K2u和K2v

(2)

2 润滑模型

准双曲面齿轮传动的接触润滑问题可简化为如图3所示的椭圆接触模型,卷吸速度方向与椭圆的短轴成一夹角,其中a、b分别为赫兹接触椭圆的短、长半轴,ue为综合卷吸速度,us为滑动速度,u1、u2分别为两表面的速度矢量,θ是ue与x方向的夹角。

图3 准双曲面齿轮润滑分析的椭圆接触模型

因此,考虑沿y方向卷吸速度的准双曲面齿轮传动的雷诺方程为

(3)

膜厚方程为

(4)

式中:V(x,y)为接触表面的弹性变形,表达式如下

(5)

压力密度方程为

(6)

压力黏度方程为

(7)

式中:Z为黏压系数。

载荷平衡方程为

(8)

3 数值计算

方程(4)～(8)中,弹性变形及润滑油黏度和密度都是压力的函数,将其与雷诺方程合并成一个微分积分方程组,采用复合迭代法[1,9]求解。弹性变形的计算采用的是快速傅里叶变换方法[12-13],其基本思想是把压力和影响系数矩阵变换到频域,将弹性变形的计算式变为影响系数和压力离散傅里叶变换的对应项相乘的关系,使计算量大大减少。

闪温的升高主要发生于压力和剪切应变速率高的接触区域,因此,本文采用考虑温度效应的非牛顿模型来预测表面闪温。表面闪温的计算采用移动热源模型,忽略任何垂直于运动方向的热流。假定物体A与物体B的整体环境温度分别为Tb1和Tb2,可以导出下面的第二类Volterra积分方程[14-15]

(9)

(10)

三维下表面应力分布可根据雷诺方程求解出的压力分布和式(11)进行计算[13]

a,b=x,y,z

(11)

式中:Tsx是作用于(x′,y′)点的单位切向力qx(x′,y′)在(x,y,z)点处引起的应力;Tsy是单位切向力qy(x′,y′)在(x,y,z)点处引起的应力;Tn是单位法向力p(x′,y′)在(x,y,z)点处引起的应力。

4 结果与讨论

4.1 基本参数

根据以上建立的润滑计算模型,以某乘用车后桥的准双曲面齿轮为例进行计算。齿轮齿坯参数见表1,机床加工参数见表2。小齿轮的输入转速为3 000 r/min,输入扭矩为139 N·m。根据式(1)可以得出啮合过程中的卷吸速度(ue)曲线,见图4。

表1 齿坯参数

表2 机床加工参数

轮齿材料的弹性模量为2.078×1011Pa,泊松比为0.3。润滑剂基本参数为:初始黏度η0=0.095Pa·s,黏压系数Z=1.82×10-8Pa-1,计算边界为-3≤x≤2,-2≤y≤2,网格划分为256×256。此外,目前关于准双曲面齿轮载荷分配的计算方法已经比较成熟,根据相关文献可知,轮齿接触点的弹性变形对啮合点的影响很小,可以忽略,因此,本文采用上文的啮合模型计算一对啮合副从啮入到啮出过程中各接触点的参数,各接触点的接触载荷分配系数(ε,为接触载荷与总载荷之比)来自于文献[16]。根据各啮合点的接触几何参数及载荷分配系数,可以计算出该点的最大赫兹压力,详见图5。从图中可以看出,在此工况下,准双曲面齿轮传动在啮合过程中的最大赫兹压力高达1.32GPa。

图4 各啮合点的卷吸速度曲线

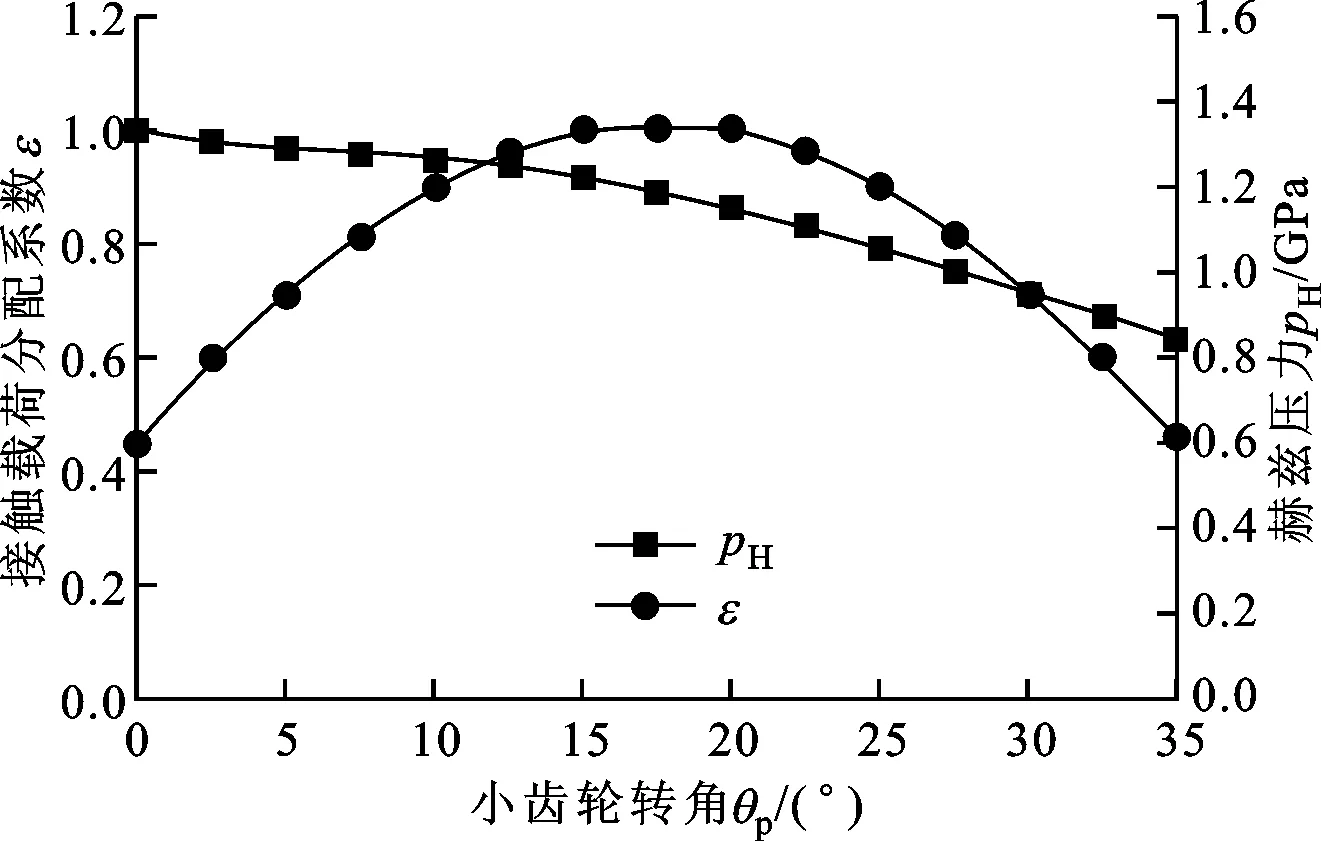
图5 各啮合点的接触载荷分配系数及最大赫兹压力

4.2 额定工况下的润滑状态分析

真实的准双曲面齿轮传动啮合点是一个接触椭圆,在按照x1=x/a、y1=y/a的方式归一化后,雷诺方程的求解域中赫兹接触椭圆转化成一个“圆”。闪温的计算是基于润滑分析所得出的油膜和压力分布的,而闪温是否产生主要取决于滑动速度矢量[15]。

(a)θ=0° (b)θ=17.5° (c)θ=35°图6 一对啮合副从啮入到啮出过程中的二维油膜压力、膜厚分布图

(a)θ=0° (b)θ=17.5° (c)θ=35°图7 一对啮合副从啮入到啮出过程中的三维油膜压力、膜厚分布图

(a)θ=0° (b)θ=17.5° (c)θ=35°图8 一对啮合副从啮入到啮出过程中的闪温分布图

(a)θ=0° (b)θ=17.5° (c)θ=35° 图9 下表面的von Mises应力

图6、图7为准双曲面齿轮传动一对啮合副从啮入到啮出过程中啮合点的归一化油膜厚度(h/a)、压力(p/pH)分布图,考虑篇幅的影响,图中显示了3个参考点。从这2个图中的压力分布图可以看出,由于准双曲面齿轮传动的卷吸速度与接触椭圆短轴有一夹角,导致压力并不沿着水平方向对称分布,且越靠近啮出点,卷吸夹角效应越明显。图8为准双曲面齿轮传动一对啮合副从啮入到啮出过程中3个等距啮合点的闪温,从中可以看出:越靠近接触点的中心,齿面的温度就越高,这主要是由于温度是压力的函数,越靠近接触中心,齿面接触压力越大,温度亦越高;同时,闪温的分布也并不沿着水平方向对称分布,这主要是因为滑动速度矢量并不与椭圆主轴重合的缘故。

图9为一对啮合副从啮入到啮出过程中啮合点表面以下的归一化vonMises应力(sv/pH)分布图。从图9中可以看出,接触点的最大vonMises应力并不在接触表面,而是在表面以下的某个位置处,这与Liu等人的研究结果[13]一致,因此,采用传统的最大赫兹压力来校核准双曲面齿轮传动的强度是不准确的。

图10为一对啮合副从啮入到啮出过程中啮合点中心油膜厚度、表面以下最大vonMises应力、表面最高闪温的变化规律。svm表示最大下表面vonMises应力,tfm表示表面最高闪温,hc表示中心油膜厚度。从图10中可以看出,从啮入到啮出的过程中,由于表面闪温是压力、膜厚以及滑动速度等变量的函数,而这3个变量的变化规律并不具有单调一致性,导致啮合点的表面最大闪温的变化呈现先升高然后逐渐降低的趋势;影响表面以下vonMises应力的主要因素是表面的压力,由于从啮入到啮出的过程中压力的分布具有单调性,因此表面以下最大vonMises应力亦呈现单调递减的趋势;中心油膜厚度在这个过程中单调递增。

图10 一对啮合副从啮入到啮出过程中最高闪温、下表面应力和中心油膜厚度的变化

4.3 转速的影响分析

在实际服役过程中,准双曲面齿轮传动常处于加速或减速工况,因此分析转速对准双曲面齿轮传动界面润滑状态的影响,具有较强的工程实用价值。图11显示了一对啮合副从啮入到啮出过程中啮合点中心油膜厚度、表面最高闪温随小齿轮转速变化的演变规律,小齿轮转速分别为500、1 000和3 000 r/min,其他输入参数完全和4.2节中的参数一致。

图11 小齿轮转速对最高闪温和中心油膜厚度的影响

从图11可以看出,小齿轮转速对准双曲面齿轮传动界面润滑状态的影响非常显著:当转速为3 000 r/min时,啮合点的润滑油膜最厚;随着转速的逐渐减小,啮合点的中心油膜厚度也随之减小;当转速为500 r/min时,啮入点的中心油膜厚度只有130 nm。由于目前准双曲面齿轮的加工精度大多只能达到6级,因此由于粗糙表面的存在,在低速情况下,准双曲面齿轮传动已处于混合润滑状态,即润滑与接触同时存在,此时界面容易因滑动摩擦发生磨损。此外,值得注意的是,转速越高,则齿面的相对滑动速度越大,啮合点的闪温越高,此时齿面越容易发生胶合失效。综上,为了最大限度地避免齿面磨损和胶合,应当合理选择准双曲面齿轮的运行转速。

5 结 论

(1)本文综合考虑了准双曲面齿轮传动的接触几何、卷吸速度与椭圆主轴不重合、润滑剂流变特性等因素,建立了用于准双曲面齿轮传动界面润滑机理分析的统一数学模型。

(2)一对啮合副从啮入到啮出的过程中,表面最高闪温的变化呈现先升高然后逐渐降低的趋势,表面以下最大von Mises应力呈现单调递减的趋势,而中心油膜厚度则单调递增。

(3)转速对准双曲面齿轮传动界面润滑状态的影响非常显著,随着转速的逐渐减小,啮合点中心的油膜厚度也随之减小,由于工程中粗糙表面的存在,界面容易因滑动摩擦发生磨损。此外,转速越高,则齿面的相对滑动速度越大,啮合点的闪温越高,因此齿面就越容易发生胶合失效。为了最大限度地避免齿面磨损和胶合,应当合理选择准双曲面齿轮的运行转速。

[1] 蒲伟, 王家序, 朱东, 等. 卷吸速度为任意方向的椭圆接触弹流润滑复合迭代解法 [J]. 机械工程学报, 2014, 50(13): 106-112. PU Wei, WANG Jiaxu, ZHU Dong, et al. Semi-system approach in elastohydrodynamic lubrication of elliptical contacts with arbitrary entrainment [J]. Journal of Mechanical Engineering, 2014, 50(13): 106-112.

[2] MARTIN H M. Lubrication of gear teeth [J]. Engineering, London, 1976, 102: 119-121.

[3] ZHU D, WANG Q. Elastohydrodynamic lubrication: a gateway to interfacial mechanics: review and prospect [J]. ASME J Tribol, 2011, 133(4): 041001.

[4] ZHU D, REN N, WANG Q. Pitting life prediction based on a 3-D line contact mixed EHL analysis and subsurface von Mises stress calculation [J]. ASME J Tribol, 2009, 131(4): 041501.

[5] SIMON V. Influence of machine tool setting parameters on EHD lubrication in hypoid gears [J]. Mechanism and Machine Theory, 2009, 44(5): 923-937.

[6] CHAO H C. A computer solution for the dynamic load, lubricant film thickness, and surface temperatures in spiral bevel gears [D]. Evanston, Illinois, USA: Northwestern University, 1982.

[7] 谷建功, 方宗德, 扶碧波, 等. 混合弹流润滑下弧齿锥齿轮齿面闪温研究 [J]. 航空动力学报, 2010, 25(12): 2846-2850. GU Jiangong, FANG Zongde, FU Bibo, et al. Study on surface flash temperature for spiral bevel gears under condition of mixed elasto-hydrodynamic lubrication [J]. Journal of Aerospace Power, 2010, 25(12): 2846-2850.

[8] 苏华, 张永红, 陈国定, 等. 弧齿锥齿轮热摩擦学行为研究的几个方面 [J]. 机械科学与技术, 2000, 19(S1): 130-132. SU Hua, ZHANG Yonghong, CHEN Guoding, et al. On spiral bevel gear’s thermal tribology behavior [J]. Mechanical Science and Technology, 2000, 19(S1): 130-132.

[9] PU W, WANG J, ZHANG Y, et al. A theoretical analysis of the mixed elastohydrodynamic lubrication in elliptical contacts with an arbitrary entrainment angle [J]. ASME J Tribol, 2014, 136(4): 041505.

[10]郑昌启. 弧齿锥齿轮和准双曲面齿轮 [M]. 北京: 机械工业出版社, 1988: 358-367.

[11]LITVIN F L. Gear geometry and applied theory [M]. Englewood Cliffs, NJ, USA: Prentice-Hall, 1994: 604-624.

[12]HU Y Z, ZHU D. A full numerical solution to the mixed lubrication in point contacts [J]. ASME J Tribol, 2000, 122(1): 1-9.

[13]LIU S B, WANG Q. Studying contact stress fields caused by surface tractions with a discrete convolution and fast Fourier transform algorithm [J]. Journal of Tribology, 2002, 124(1): 36-45.

[14]MARTINI A, ZHU D, WANG Q. Friction reduction in mixed lubrication [J]. Tribology Letters, 2007, 28(2): 171-181.

[15]ZHU D, CHENG H S. An analysis and computational procedure for EHL film thickness, friction and flash temperature in line and point contacts [J]. Tribology Transactions, 1989, 32: 364-370.

[16]HUANG C, ZHENG C, LI R. An analysis system of loaded tooth contact behavior of spiral gears [J]. Progress in Nature Science, 1992, 2(6): 556-560.

(编辑 葛赵青)

Analysis on Lubrication Performance of Hypoid Gears at Heavy Loads

PU Wei1,WANG Jiaxu1,2,YANG Rongsong1,ZHU Dong1,ZHOU Guangwu1,WU Jiqiang1

(1. School of Aeronautics and Astronautics, Sichuan University, Chengdu 610065, China;2. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China)

A unified lubrication model is established for hypoid gears considering the effects of contact geometry, the oblique angle between entrainment speed and principal axis of ellipse, as well as rheological properties. The pressure, film thickness, flash temperature and von Mises stress are obtained at different meshing points from beginning to the end of whole engagement process under heavy load conditions. Besides, the effect of speed on the lubrication performance is also studied. The results reveal that both the central film thickness and the max von Mises stress show a monotone decreasing tendency during the whole engagement process; the max flash temperature increases first and then gradually decreases; and the effect of rotational speed on the lubrication performance in contact surface is significant. The central film thickness decreases gradually with the decrease of rotational speed, leading to abrasion due to the sliding friction on rough surface. In addition, the higher the rotational speed is, the larger the flash temperature will be, which may lead to scuffing failure on the contact surface. Therefore, in order to avoid abrasion and scuffing failure as much as possible, it is necessary to properly select the rotational speed of hypoid gears.

hypoid gear; heavy load; flash temperature; von Mises stress

2015-03-13。

蒲伟(1989—),男,博士生;王家序(通信作者),男,教授,博士生导师。

国家自然科学基金资助项目(51435001,51375506)。

时间:2015-08-26

10.7652/xjtuxb201511010

TH132

A

0253-987X(2015)11-0055-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150826.1117.004.html