液滴与水平壁面碰撞力的实验方法

张彬,郭朋华,李景银

(西安交通大学能源与动力工程学院,710049,西安)



液滴与水平壁面碰撞力的实验方法

张彬,郭朋华,李景银

(西安交通大学能源与动力工程学院,710049,西安)

为了获得准确的碰撞力数据,根据液滴碰撞过程极其短暂且低速液滴碰撞力较小的特点,搭建了低速液滴与固体壁面碰撞力测量实验台;通过理论分析和实验验证对液滴碰撞力测量系统进行了优化,以探究系统振动对瞬态碰撞力结果的影响;利用滤波等措施消除影响后获得低速液滴和固体壁面碰撞过程的碰撞力。实验中使用压电传感器来测量碰撞力随时间变化的过程,同时将测量系统简化为双振子模型,以分析基座和碰撞盘的振动对碰撞力信号的影响;通过进行实验结果的频谱分析来验证理论模型,同时找出影响碰撞力信号波动的因素。实验表明:基座和碰撞盘的振动会导致碰撞力曲线出现波动,增大基座质量可以消除基座振动的影响,减小碰撞盘的质量并结合低通滤波可以消除碰撞盘振动的影响。测试系统可以实现不同液滴直径、不同碰撞速度和物性的液滴碰撞力的采集和处理。

液滴碰撞;碰撞力;压电传感器;振动;滤波

液滴与固体壁面的碰撞现象广泛存在于能源、化工、航空以及农业等领域,由于液滴碰撞导致的材料侵蚀以及水土流失的问题一直以来都备受科研工作者的关注[1-4]。液滴与固体壁面碰撞过程中碰撞力(或压强)的产生和传播是分析以上问题的关键。

液滴碰撞力的瞬态过程极其短暂,低速液滴的碰撞力较小,因而实验测量难度较大。Portemont等人使用压电传感器获得了水滴碰撞压强随时间的变化规律,然而传感器自身存在空腔结构,空腔中空气会影响结果的准确性[5];Nearing等人使用压电传感器测量不同直径液滴由14 m高度落下时的碰撞力,该液滴速度(8.32～9.28 m/s)远小于由自由落体定律所得速度(16.57 m/s),即液滴在长距离下落过程中因为速度较大而受空气阻力的作用显著,可推断液滴形状发生了显著变化,进而实验所得数据并非原有球形液滴的碰撞力,同时受限于传感器尺寸,该实验方法无法测量大直径液滴的碰撞力[6];Grinspan等人采用自制的压电传感器测量了液滴碰撞力[7],但实验结果因为压电薄膜的反弹而出现碰撞力负值。

合理的实验方法是准确获取液滴碰撞力的关键,因此本文在合理设计实验的基础上,通过理论分析和实验验证对液滴碰撞力测量系统进行了优化,以探究系统振动对瞬态碰撞力的影响,通过滤波等措施消除影响后获得了低速液滴与固体壁面的碰撞力。

1 实验装置及实验方法

图1 实验装置示意图

实验装置示意图如图1所示。通过合理设定高精度注射泵推进速率,在平口针头处可形成液滴并按自由落体方式下落。铝制圆形碰撞盘将碰撞力通过碰撞盘下部的螺纹传递给传感器内的压电薄膜。碰撞盘的直径要足够大,以防止液滴在铺展过程中溢出盘面,进而保证完整记录铺展过程中碰撞力的变化。传感器与基座的装配方式如图2所示。实验中采用了Kistler 9215型压电力传感器,其固有频率大于50 kHz。该传感器对小于5、10、15、17.5 kHz的频率,其信号幅值的测量误差分别小于1%、5%、10%、14%。液滴碰撞力经过傅里叶变换后所得频率为小于5 kHz的宽频部分,碰撞盘的振动频率小于17.5 kHz,该传感器可以实现对所关注信号的准确测量。

图2 传感器装配示意图

采用电荷放大器(Kistler 5018A型)将电荷信号转换为一定比例的电压信号,采用高绝缘电缆连接传感器和电荷放大器,采用Dewe-43数据采集系统和计算机内配套软件实现电压信号的采集和存储。采集系统的采样频率设定为100 kHz,该频率高于所关注频率的两倍,以便满足奈奎斯特的采样定理。

实验中要防止注射泵、电脑等自身振动影响采集结果,通过更换不同直径的针头形成不同直径的液滴,通过改变针头到碰撞盘壁面的垂直距离来实现不同的液滴碰撞速度。

若低速液滴与固体壁面碰撞前保持球形,则液滴直径

(1)

式中:ρ是液体密度;m是n个液滴总质量。液滴质量采用精度为0.001 g的电子天平称量,液滴的总质量为100个测量液滴的总和,重复实验5次以减小系统误差。

液滴碰撞速度的确定通常有两种方法:自由落体计算法和高速摄影测量法。文献[8]指出:对低速液滴,采用自由落体方法计算所得碰撞速度与高速摄影测量所得速度仅相差3%。本文采用自由落体方法计算液滴与壁面碰撞时的初始碰撞速度,即

(2)

式中:H是针头顶部到碰撞盘壁面的距离;g是重力加速度。

2 系统振动因素的理论分析

研究中发现,碰撞盘和基座等系统部件的振动对数据采集有显著影响,因此将图2所示的碰撞盘、传感器和基座简化为双振子耦合系统,如图3所示。该系统不考虑阻尼的影响,其中碰撞盘简化为不计体积的质量块m1和刚度k1的无质量弹簧,传感器和基座组合简化为不计体积的质量块m2和刚度k2的无质量弹簧。下部固定点为坐标原点,静止状态下m1、m2位于平衡位置x1、x2。

图3 双振子耦合系统示意图

质量块由平衡位置移动到当前时刻位置所运动的距离为u,对于二自由度振动,该系统的动力学方程为

(3)

(4)

式(3)、(4)的普通解为

式中:A1和A2为振动的振幅;ω为振动角频率;φ为相位。将普通解代入式(3)、(4)可得

(5)

(6)

要使A1、A2有非0解,以上方程组的系数行列式应为0,即

(7)

求解式(7)可得

(8)

求解式(8)可得

(9)

一般情况下,ω有两个不同的正解,当m2远大于m1时,m2为分母的相可近似为0,此时ω2=k1/m1,即

(10)

尽量减小系统振动对采集信号的影响是实验中获取可靠数据所秉持的原则,因此由以上理论分析可知,采用大质量基座(m2)可以减小或消除基座振动对信号采集的影响,同时碰撞盘的质量(m1)也是影响系统振动频率的主要因素。

3 系统振动因素的实验研究

选用质量为0.8、50 kg的2个基座分别命名为基座A和基座B,同时选用质量为11.670、3.903、0.995 g的3个铝制碰撞盘依此命名为碰撞盘A、碰撞盘B、碰撞盘C,所用液滴为不同直径和碰撞速度的蒸馏水液滴(下文简称水滴)和甘油液滴。

3.1 基座对碰撞力信号的影响

选用基座A和碰撞盘A组合的碰撞系统测量了水滴的瞬态碰撞力,水滴的直径为3.54 mm,碰撞速度为2.80 m/s(后文中若无特殊说明,则实验数据均为该水滴碰撞所得)。水滴的碰撞力原始数据的时域曲线如图4所示。可以看出,初始阶段水滴碰撞力迅速增大,到达峰值后缓慢下降,整个过程中数据都存在明显的波动。由上文系统的理论分析推测,该波动可能源于系统部件的振动。鉴于在振动分析领域,频谱分析相较时域分析更有优势,所以采用快速傅里叶变换算法将图4数据转换为频谱图,如图5所示。可以看出,碰撞力信号存在3个特殊频率:处于低频区域内的宽频域α,2.2 kHz左右的频率峰值β,5.3 kHz附近的频率峰值γ。

图4 选用基座A和碰撞盘A时原始数据的时域特性

将基座A换成基座B,使用相同碰撞盘A、采集同样直径和碰撞速度的水滴的瞬态碰撞力的频域特性如图6所示。与图5中曲线相比,图6中曲线无β,这说明β与基座有关。由式(9)、(10)可知,当基座质量远大于碰撞盘质量时,基座的振动可减小或消除,此时系统的振动可视作碰撞盘的单振子振动。由此可推断,图5中β即为基座A的振动频率,而图6中无β是因为基座B质量足够大,以至于水滴碰撞已无法激励共振发生。

图5 选用基座A和碰撞盘A时原始数据的频域特性

图6 选用基座B和碰撞盘A时原始数据的频域特性

由实验数据可知,直径为3.54 mm、碰撞速度为2.80 m/s的水滴碰撞力持续时间为2 ms。在碰撞力持续时间内,要消除基座振动的影响,应使基座振动周期大于2 ms,即基座振动频率小于500 Hz。由上文分析可知,质量0.8 kg的基座A的β为2 200 Hz。假设增加基座质量后其刚度变化很小,那么要保证基座固有频率小于500 Hz,则需要基座质量达到15.5 kg以上。为确保基座振动频率远小于500 Hz,实验中采用的基座B的质量为50 kg。

以上实验结果验证了本文的理论分析,同时进一步说明选取大质量的基座可以减小基座振动对碰撞力信号的影响。

3.2 碰撞盘对碰撞力信号的影响

使用基座B和碰撞盘A组合的采集系统分别记录了水滴和钢球(D=1.0 mm,V=1.40 m/s)与固体壁面的碰撞力,该碰撞力的频谱信号如图7所示。可以看出,γ同时存在于水滴和钢球碰撞力频谱中,而α仅在水滴频谱中出现。因为钢球的碰撞时间极短,仅相当于给予系统一个振动激励,所以钢球碰撞所得频谱中的γ为碰撞盘的振动频率;又因水滴碰撞和钢球碰撞都会引起碰撞盘振动,所以两曲线中都存在γ。相较于钢球与壁面的碰撞过程,在碰撞过程中低速水滴粘附于壁面且施加作用力的时间较长。液滴塑性碰撞所施加的力同钢球弹性碰撞所施加的力有所不同,这导致了两者在频谱中的低频区域出现差别。由此推断:位于低频区域的α与水滴的碰撞力有关。

图7 水滴和钢球碰撞力的频谱对比

使用相同参数的水滴与碰撞盘A、B、C分别碰撞,其碰撞力变化过程的频域特性如图8所示。可以看出,在低频区域,不同碰撞盘的碰撞力有着相同的α,但各自的γ却不相同,对于碰撞盘A、B、C,其各自的γ分别为5 371、6 494、16 845 Hz,即γ的数值随碰撞盘质量的减小而增大。该实验现象同式(10)揭示的振动频率与质量的关系一致。由此可进一步推断,γ源于碰撞盘的振动。

图8 不同质量碰撞盘碰撞力的频谱图

3.3 液滴参数对系统频谱特性的影响

相同碰撞速度(2.43 m/s)、不同直径(2.28、2.48、2.73 mm)水滴的碰撞力频谱特性如图9所示。可以看出,随水滴直径的增大,频谱的幅值增大,而α横坐标数值范围变化较小且γ无变化。

图9 水滴直径对频谱特性的影响

同一直径(2.28 mm)的水滴,改变其碰撞速度(1.98、2.43、2.80 m/s)后的碰撞力频谱特性如图10所示。可以看出,随碰撞速度的增大,频谱的幅值增大,而α横坐标数值范围变化较小且γ无变化。

图10 水滴碰撞速度对频谱特性的影响

相同直径(3.54 mm)、相同碰撞速度(2.43 m/s)水滴和甘油液滴的碰撞力频谱特性如图11所示。可以看出,甘油液滴的碰撞力频谱特性规律与水滴相同,表明物性对α横坐标数值范围的变化影响较小且对γ无影响。可见,不同的参数液滴对液滴碰撞过程中频谱特性的影响却相同,这有助于采用相同的实验方法测量并获取不同参数液滴的碰撞力。

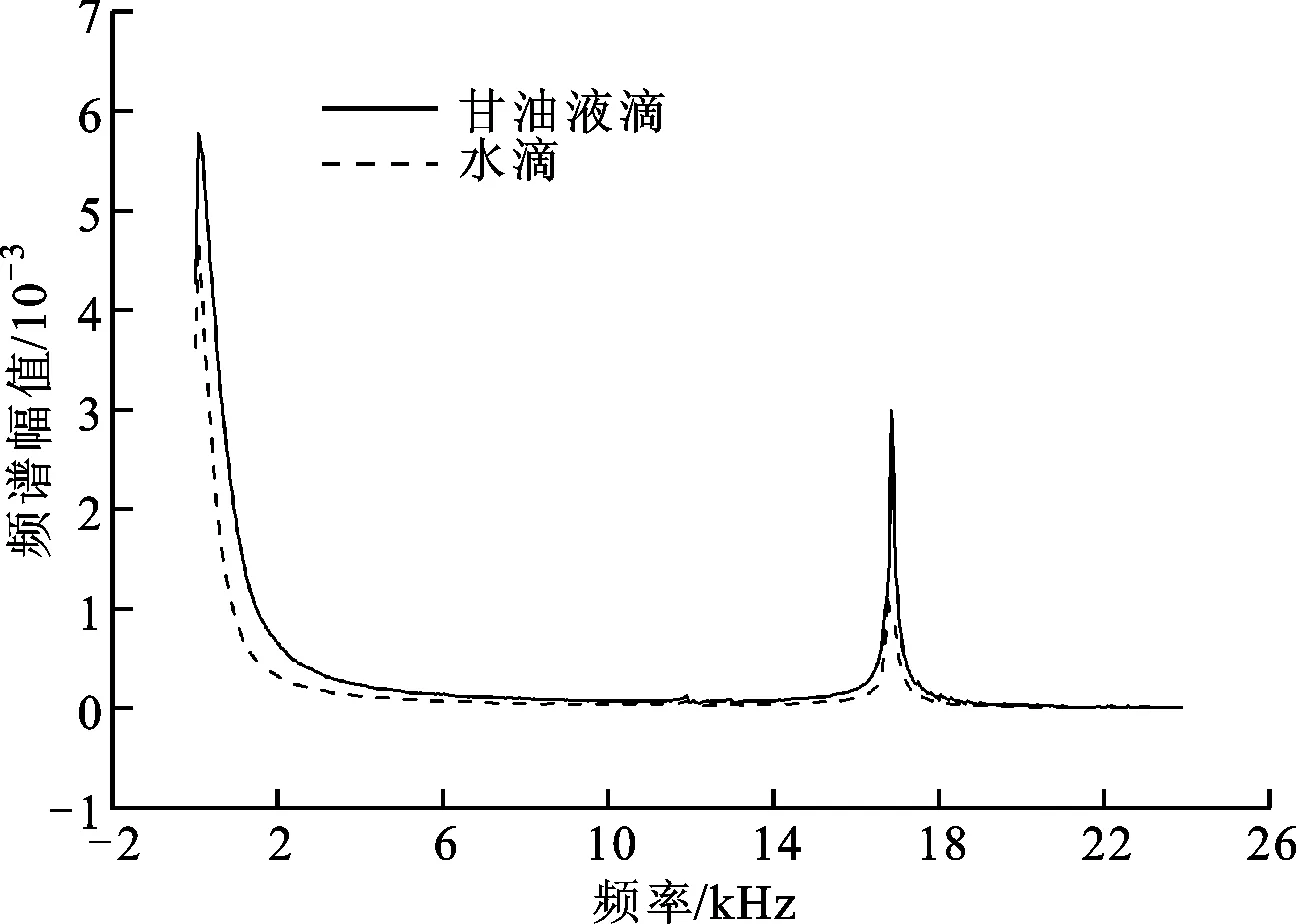
图11 水滴和甘油液滴碰撞力频谱特性

4 结果和讨论

4.1 真实碰撞力获取

处于低频区域的α与液滴碰撞力有关,要获取液滴碰撞力的真实值,可以通过滤波手段将处于高频的碰撞盘振动频率消除。本文采用带有哈明(Hamming)窗的有限脉冲响应(FIR)低通滤波器来消除γ的影响,选用哈明窗函数是因为其主瓣具有较小的旁瓣和较大的衰减速度。由图8可知,碰撞盘质量越小,其引起的γ就越发远离与液滴碰撞力有关的α。因此,使用小质量盘可有效减小低通滤波对获取液滴碰撞力的影响。低通滤波截止频率的选取要兼顾滤波后信号的光滑性及目标信号的完整性,即滤波在消除液滴碰撞力原始信号中波动的同时,应尽量减小对真实碰撞力信号的影响。经综合考虑,数据处理过程中低通滤波器的截断频率可统一设为11 000 Hz,滤波程序的编写和相关数据处理由Matlab软件实现。

采用基座B和碰撞盘C时,直径为3.54 mm、碰撞速度为2.80 m/s的水滴在滤波前后的瞬态碰撞力对比如图12所示。滤波后原始信号中的波动现象消失,碰撞力即为液滴与壁面碰撞的真实碰撞力,碰撞力最大值比滤波前减小约19%且下降阶段末期无负值出现。滤波后的碰撞力在初始阶段快速上升,到达最大值之后缓慢下降,经历约2 ms后趋于平衡,此时碰撞力数值为0。滤波后所得真实液滴碰撞力随时间的变化曲线为非周期、非线性的,其傅里叶变换所得频率在频谱中是宽频域,并非单个频率峰值,这再次证明α是液滴碰撞力的傅里叶变换所得。

图12 滤波前后碰撞力数据对比

4.2 碰撞力研究对比

本文实验所得水滴碰撞力(D=3.54 mm,V=2.80 m/s)与文献[7]实验所得水滴碰撞力(D=3.57 mm,V=2.78 m/s)随时间的变化如图13所示。可以看出:在所用水滴参数相近的情况下,文献[7]中碰撞力峰值比本文实验所得碰撞力峰值大近一个数量级;文献[7]中碰撞力在上升阶段和下降阶段共历时约600 μs,而本文实验共历时长达约2 ms,文献[7]中碰撞力在600～2 000 μs之间出现了负值。实验记录的液滴碰撞力过程正是液滴相对固体壁面的冲击过程,液滴对壁面的碰撞力应该是始终指向壁面,即在碰撞的初期和铺展阶段,液滴碰撞力应始终为正值,不会出现负值。在其他有关碰撞力或碰撞压强的实验[6]以及数值模拟[9-10]中,碰撞力和碰撞压强随时间变化也均为正值。相比文献[7],在获取液滴与壁面碰撞的瞬态碰撞力方面,本文采用成熟的压电传感器以及精心设计的实验方法是可行、可靠、准确的。

图13 本文与文献[7]实验碰撞力随时间的变化

5 结 论

通过搭建低速液滴碰撞力测量实验台探究了系统振动以及液滴参数对数据采集的影响,并得出以下结论。

(1)基座和碰撞盘的振动都会影响碰撞力测量的准确性,本文的理论分析和实验研究同时表明:选用大质量基座可消除基座振动的影响,选用小质量碰撞盘时,通过结合低通滤波可消除碰撞盘振动的影响。

(2)液滴直径、碰撞速度以及液滴物性等因素对碰撞力宽频域的数值范围无明显影响。本文碰撞力测量系统可对不同参数液滴的碰撞力进行准确、可靠的测量,可获取低速液滴冲击固体壁面的碰撞力。

[1] GOHARDANI O. Impact of erosion testing aspects on current and future flight conditions [J]. Progress in Aerospace Sciences, 2011, 47(4): 280-303.

[2] MOUZAI L, BOUHADEF M. Shear strength of compacted soil: effects on splash erosion by single water drops [J]. Earth Surface Processes and Landforms, 2011, 36(1): 87-96.

[3] KEEGAN M H, NASH D H, STACK M M. Modelling rain drop impact of offshore wind turbine blades [C]∥ASME Turbo Expo 2012. New York, USA: ASME, 2012: 887-898.

[4] AHMAD M, SCHATZ M, CASEY M V. Experimental investigation of droplet size influence on low pressure steam turbine blade erosion [J]. Wear, 2013, 303(1): 83-86.

[5] PORTEMONT G, DELETOMBE E, DRAZETIC P. Assessment of basic experimental impact simulations for coupled fluid/structure interactions modeling [J]. International Journal of Crashworthiness, 2004, 9(4): 333-339.

[6] NEARING M A, BRADFORD J M, HOLTZ R D. Measurement of force vs. time relations for waterdrop impact [J]. Soil Science Society of America Journal, 1986, 50(6): 1532-1536.

[7] GRINSPAN A S, GNANAMOORTHY R. Impact force of low velocity liquid droplets measured using piezoelectric PVDF film [J]. Colloids and Surfaces: A Physicochemical and Engineering Aspects, 2010, 356(1): 162-168.

[8] MAO T, KUHN D C S, TRAN H. Spread and rebound of liquid droplets upon impact on flat surfaces [J]. AIChE Journal, 1997, 43(9): 2169-2179.

[9] 张彬, 韩强, 袁小芳, 等. 液滴与水平壁面碰撞力的数值研究 [J]. 西安交通大学学报, 2013, 47(9): 23-27. ZHANG Bin, HAN Qiang, YUAN Xiaofang, et al. Simulation of impact force of drop impacting on horizontal plate [J]. Journal of Xi’an Jiaotong University, 2013, 47(9): 23-27.

[10]LI R, NINOKATA H, MORI M. A numerical study of impact force caused by liquid droplet impingement onto a rigid wall [J]. Progress in Nuclear Energy, 2011, 53(7): 881-885.

(编辑 苗凌)

Experimental Research on Impact Force of Drop Impacting on Horizontal Plate

ZHANG Bin,GUO Penghua,LI Jingyin

(School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

The force of a low-speed drop impacting on the wall is tiny with a short duration. To measure the impact force precisely, an experimental rig was developed by adding a high-precision piezoelectric sensor. The measuring system was optimized based on both theoretical analysis and experimental verification, and the effect of system vibration on the transient impact force was investigated. The precise impact force can be obtained in terms of filters and other measures to eliminate the signals of the system vibration. In this approach, a double oscillator model was adopted to analyze the effect of the substrate and impact plate masses on the impacting force signal. Then the experimental frequency spectrums were compared to verify the vibration model, and the factors causing the fluctuation of force signals were determined. It is found that the vibration of the substrate and the impact plate is responsible for the fluctuation of force signal, which can be eliminated by choosing a very heavy substrate and a light impact plate combined with low-pass filter. Such an improved experimental system can measure the impact force of drops with different properties, diameters and impact velocities.

drop impact; impact force; piezoelectric sensor; vibration; filter

2015-01-31。

张彬(1989-),男,博士生;李景银(通信作者),男,教授,博士生导师。

国家自然科学基金资助项目(51276137,51406155)。

时间:2015-08-13

10.7652/xjtuxb201511002

TK05

A

0253-987X(2015)11-0008-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150813.1012.004.html