离心风机集流器的响应面优化设计

赵燕杰,谭俊飞,党飞龙,李景银

(1.西安交通大学能源与动力工程学院,710049,西安;2.中冶赛迪工程技术股份有限公司,400013,重庆)



离心风机集流器的响应面优化设计

赵燕杰1,谭俊飞2,党飞龙1,李景银1

(1.西安交通大学能源与动力工程学院,710049,西安;2.中冶赛迪工程技术股份有限公司,400013,重庆)

对某高效低噪音离心风机的集流器进行了优化设计研究,首先通过数值计算得到了在初始设计的集流器扩张角、集流器收缩角和扩张段长度等参数下的离心风机气动性能,并与实验结果进行对比验证,在此基础上采用响应面方法进行二次回归拟合,得到了锥弧型集流器扩张角、收缩角和扩张段长度与风机效率及声功率级之间的函数关系并进行了优化分析,由此得到使风机性能最优的集流器参数。分析结果表明,锥弧型集流器对离心风机气动性能的影响比较显著,对声功率级的影响不太显著,锥弧型集流器的扩张角、收缩角对离心风机气动性能的影响明显,而集流器扩张段长度对气动性能的影响很小。优化后的集流器使得离心风机的效率提升了3.6%,静压提高了4.1%,声功率级降低了1.7 dB。

离心风机;集流器;响应面法;声功率级

集流器作为离心风机三大部件之一,起着降低流动损失、将气流平稳均匀送入叶轮的作用[1]。气流由集流器进入叶轮时会在叶轮进口附近形成一个涡流区,从而影响到叶轮中前盘附近的气体流动状况,因此集流器结构和安装位置会对风机性能有很大影响。

国内外学者对于离心风机内部的流动状况及机理进行了广泛的研究[2-5]。Refeal等通过数值研究发现,叶道内部的三维非对称流动与集流器结构参数有着直接的关系[6]。Montazerin等通过改进集流器结构使风机内部气流流动得以改善[7-8]。温选锋等采用实验方法研究了椭圆形集流器对多翼离心风机气动性能及噪音的影响[9]。徐文明等研究发现,收敛型集流器进口倾斜角度对风机的气动性能会产生较大影响,而对噪音的影响则很小[10]。杨昕等以双吸前向多翼风机为例实验研究了集流器的偏心安装位置对风机性能及噪声的影响[11]。王嘉冰等采用数值模拟方法研究了集流器安装位置对叶道内气流分布及风机性能的影响[12]。

本文首先采用数值模拟方法研究了离心风机中常用的锥弧型集流器结构参数对其气动性能及噪声的影响,并与实验结果进行了对比验证。在此基础上,结合响应面方法拟合出锥弧型集流器扩张角、收缩角和扩张段长度这3个关键参数与风机气动性能和气动噪声的函数关系式,从而对集流器参数进行了优化,以提高离心风机的效率、降低噪声。

1 物理模型及数值计算和验证

1.1 离心风机各部件几何参数

离心风机主要包括集流器、叶轮和蜗壳三部分,其中集流器的结构如图1所示。叶轮是由16个周向均布的后向叶片及轮盘、轮盖组成的闭式叶轮。蜗壳型线主要由4段圆弧组成,各部件主要结构参数如表1所示。风机的设计流量qv=0.65 m3/s,设计转速n=2 900 r/min。

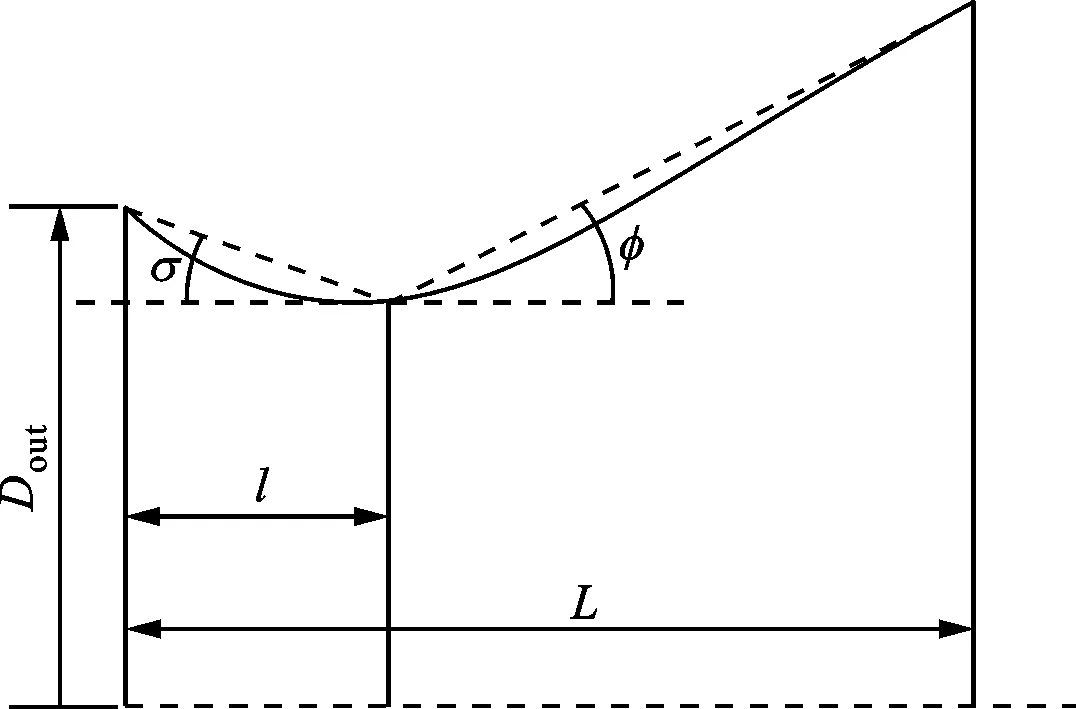
图1 集流器结构及主要参数

参数 数值叶轮叶片出口直径D2/mm481叶轮叶片进口直径D1/mm220叶轮进口直径D0/mm209叶轮进口宽度b1/mm63.64叶轮出口宽度b2/mm24.54叶轮叶片数Z16叶片进口安装角β1A/(°)27.2叶片出口安装角β2A/(°)82蜗壳宽度B/mm108蜗舌半径R/mm28集流器总长度L/mm40扩张段长度l/mm10扩张角σ/(°)30收缩角ϕ/(°)25

1.2 离心风机内部数值计算方法

本文采用商业软件Ansys Fluent模拟了风机内部的流动,获得了离心风机的气动性能与气动噪声,同时在建模过程中忽略了集流器与叶轮套接部分径向间隙造成的内泄漏流动。风机叶轮网格在Turbo Grid中生成,集流器及蜗壳网格在ANSYS Icem中生成。为了提高近壁面区域流动计算的准确性,对叶轮内部、蜗壳蜗舌壁面附近的网格进行了加密控制和非等距处理,同时对计算网格进行了网格无关性验证,由此得到集流器、叶轮和蜗壳的网格数分别约为16万、96万和87万,整机网格数约为199万,如图2所示。

由于风机内部流动马赫数小于0.3,属于不可压缩流动,所以对离心风机的气动性能采用定常计算。定常流动计算时采用了多参考系(MRF)方法,叶轮区域在相对坐标系下求解,集流器和蜗壳区域在静止坐标系下求解,动静交界面用来传递信息。风机进、出口边界条件分别为流量进口、静压出口,湍流模型为Realizablek-ε湍流模型,稳态流场采用SIMPLEC算法计算。

发动机服务性资料模块化数据配置管理的研究………………………… 闫玉，刘栋，李小燕，谭磊，傅连朋（1-273）

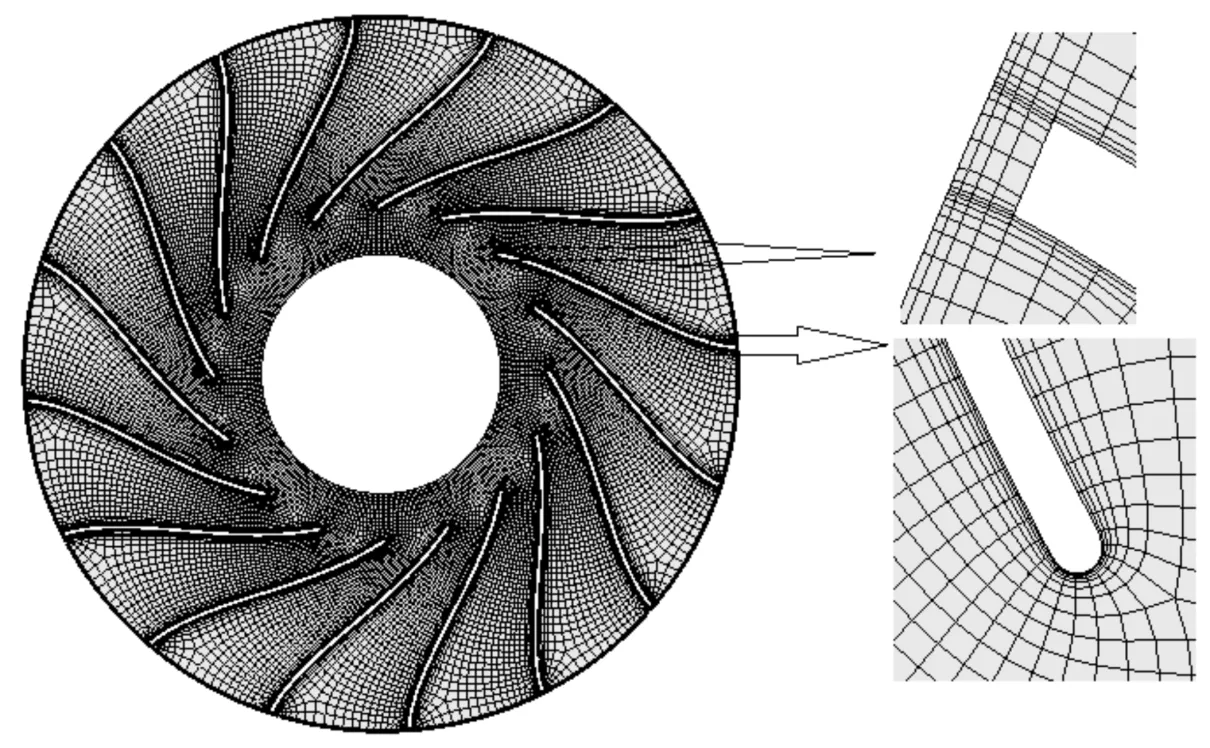
(a)叶轮网格

(b)集流器网格

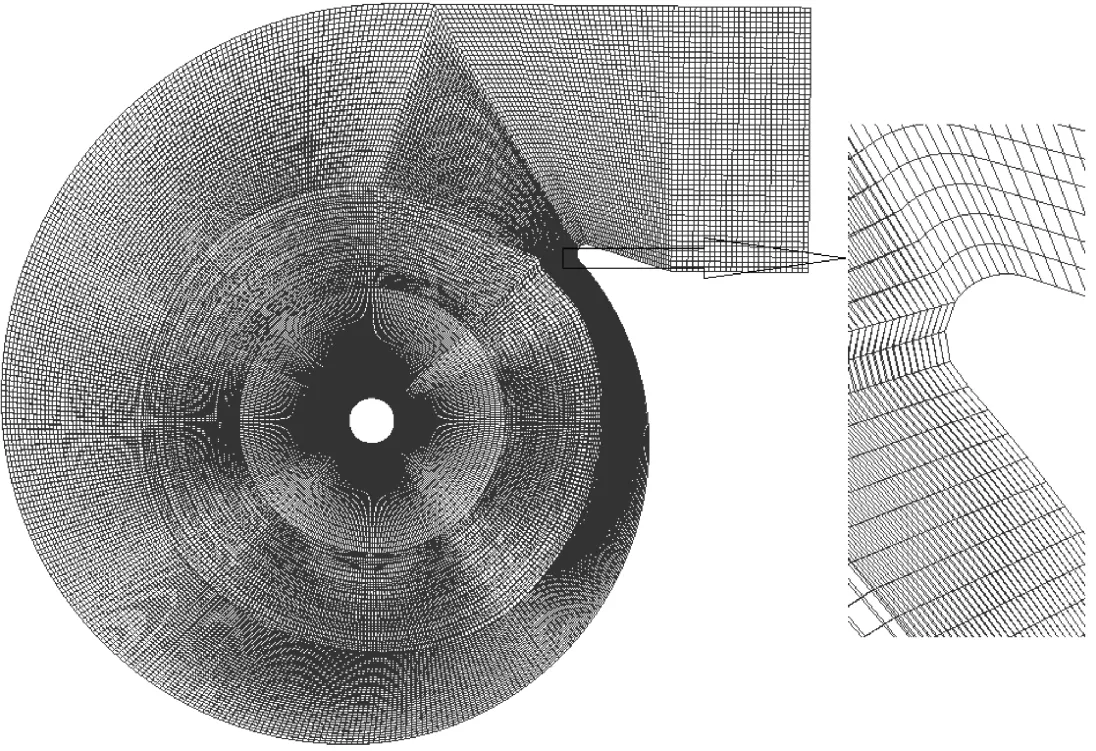
(c)蜗壳网格图2 离心风机网格

采用上述的计算模型、网格和数值计算方法对原始设计的风机模型进行了数值计算,由此得到设计流量下风机的静压Pst、总压Ptot和效率η,并与实验进行了对比,结果如表2所示。由表中结果可以看出,在设计工况(流量为0.65 m3/s)下,η最大误差约为2.1%,静压Pst最大误差约为1.9%,表明了本文数值计算方法的准确性。

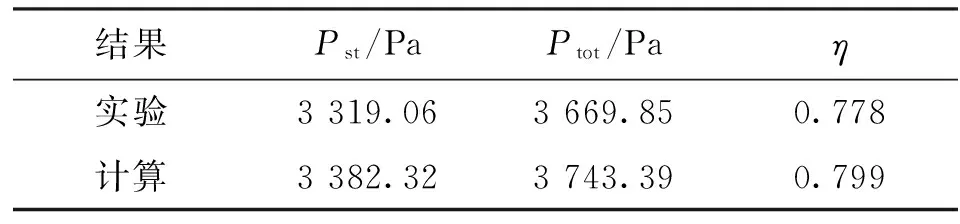
表2 设计流量下实验与计算结果比较

在模拟非定常流动时,采用滑移网格(SM)技术处理各部件之间(集流器-叶轮、叶轮-蜗壳交界面)的信息传递,将定常计算结果作为非定常的初值进行计算,收敛后激活Fluent声学模块,并利用FW-H方程预测离心风机噪声,由此获取声源信息。选择PISO算法求解非定常流动,而非定常流动中时间步长计算式如下

(1)

式中:n为转速;K为单流道计算步数,本文中K=30;Z为叶片数。

使用FW-H方程预测噪声时忽略了四极子源的影响,离心风机中的所有墙(Wall)将作为声源,对数值计算得到的关于时间的离散声压进行FFT变换,进而得到监测点上的线性声压级。声功率级是声源在单位时间内向外辐射出的总声能,本文根据ISO3745—2012[13]、采用包络面法在离心风机的包络面上布置了20个检测点,通过测量检测点上的声压级,再由以下公式合成声功率级

(2)

(3)

式中:Lpi表示检测点i的声压级;Lw表示声功率级;S1表示包络面的面积;S0表示参考面积。

2 集流器优化结果与分析

2.1 响应面方法

响应面方法是用来对设计目标(响应)受多个设计变量(因素)影响的问题进行建模和分析的方法,目的是优化响应,包括实验设计、方程回归、回归方程检验和最优化求解等。

(4)

(5)

其中k=1,2,…,m-1(j≠k)。

通过实验设计,如中心复合设计(CCD)或Box-Behnken设计等,可以获得一系列样本点,响应面方程的建立就是对这些实验点进行回归的过程。对于求解模型中的各个待定系数,通常采用最小二乘法进行。在确定回归方程后还要进行显著性检验,包括方程显著性检验、偏回归系数检验和失拟性检验,回归方程显著性、失拟不显著性是回归方程可以用于预测优化的前提。首先通过实验设计建立回归方程,再经过检验得到可以用于预测优化的数学模型,然后根据极值存在的条件得到最佳值,也可以通过绘制响应面或等高线图来直观显示预测的最佳值。要保证响应变量取得最佳值时的设计变量取值落在实验范围内,可能需要通过多次实验来确定设计变量所在的范围。

2.2 实验设计及参数选择

集流器的主要参数(如图1所示)包括L、σ、φ、l。本文通过响应面方法,研究集流器的σ、φ、l对风机性能及气动噪声的影响。

L为40 mm、出口直径Dout为207 mm、集流器特征参数γ=L/Dout=0.02,σ、φ、ε作为实验因素,ε=l/L。初始选定的取值范围为ε=0.2～0.35,σ=15°～40°,φ=20°～40°,响应变量选择效率与声功率级。采用Box-Behnken方法进行实验设计,Design-Expert软件给出实验设计方案,如表3所示。

表3 Box-Behnken实验设计方案

各实验方案计算结果如表4所示。分析表4中的数据可以发现,在集流器各因素取值范围内,集流器结构参数对离心风机的声功率级影响很小,对气动性能影响较大。因此,将声功率级从响应变量中去除,仅保留效率作为响应变量,再通过回归方程得到集流器结构参数与效率之间的近似函数关系。

在Design-Expert软件中对3个实验变量的9种组合ε2、σ2、φ2、εσ、εφ、σφ、ε、σ、φ选择不同的项进行方程回归,再对拟合出来的方程进行方差分析,根据回归方程的显著性检验、偏回归系数检验、失拟性检验选择参与方程回归的项,通过多次试验便可得到较好的效率拟合方程

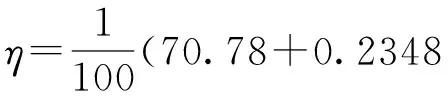
0.006118φ2-0.005836σ2)

(6)

分析发现,回归方程的显著性明显、失拟性不显著,回归方程在各个实验点拟合得很好。方程(6)中没有包含集流器的ε项,这是因为在加入该项后,通过偏回归系数检验得到的相关项对离心风机效率没有显著性影响。从回归方程可以看出,在集流器参数的取值范围内,σ、φ对离心风机的效率有显著性影响,ε则显著性影响不明显。

对满足显著性检验的方程进行预测分析,通过Design-Expert软件绘制出该回归方程的等高线图,由此求出响应变量在各因素取值范围内的最佳值,如图3所示。

图3 第一次优化效率等高线图

从图3中可以看出,在等高线图中没有出现最优点,说明选取的实验因素范围不合适,需要进行调整。进一步由图中的趋势可以判断,为了保证出现最优点,可以将σ调整为20°～50°、φ调整为0°～40°。由于ε的显著性影响不明显,因此第2次优化中仅选取σ、φ作为实验因素,同时采用CCD来安排实验。CCD实验设计各方案及数值计算结果如表5所示。

表5 CCD实验点设计及计算结果

通过Design-Expert软件对计算结果进行方程回归分析,经过不断调整参与拟合的项,得到满足显著性检验的回归方程

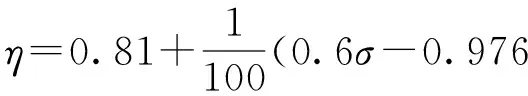
(7)

分析发现,该回归方程的显著性明显、失拟性不显著,回归方程在各个实验点拟合得很好。根据回归方程绘制等高线图如图4所示。

图4 第2次优化效率等高线图

由图4中可以看出,在等高线图中存在最优点,即响应变量可以在实验因素的范围内得到极大值。对回归方程进行最优化求解,即可得到最佳值。

2.3 结果验证及分析

由回归方程最优化求解结果显示,当σ为42.8°、φ为23.8°时,回归方程的响应变量η最高。在集流器设计参数中,由于ε的影响不显著,因此改进后的l仍然保持不变。对优化后的风机模型进行数值计算,得到设计流量(0.65 m3/s)下风机的性能及声功率级,并与模型优化前的计算结果进行了对比,如表6所示。

表6 改进前后风机设计工况下气动性能及声功率级

为了验证优化结果的可靠性,本文还对集流器优化后的风机性能进行了实验测试,实验遵循了GB/T1236—2000[14]、采用了进口侧实验风筒装置。改进前后风机在设计工况(0.65 m3/s)下的性能实验结果如表7所示。

表7 改进前后风机设计工况下性能实验结果对比

对比表6和表7可以发现,集流器改进前后风机性能的计算结果与实验值都在允许的误差范围内,并且趋势一致。由表7还可以看出,采用响应面法对集流器结构参数进行优化后,离心风机的静压升高了4.1%,总压提升了3.9%,效率提高了3.6%。

集流器优化前后风机内部流场的分布如图5所示。可以看出,集流器优化后风机主流区大部分流道的流动性能得到了改善,流动的非对称性减弱,吸力面低速区减小,只有在靠近蜗舌附近的流道内流动性能恶化。

(a)集流器优化前 (b)集流器优化后图5 集流器优化前后50%叶高处截面流线图

3 结 论

本文采用数值模拟与响应面相结合的方法,对某高效、低噪声离心风机集流器参数进行了优化研究,通过对气动性能及噪声的分析,得到以下结论。

(1)将数值模拟方法与响应面方法相结合,能够应用于离心风机的改进和优化。

(2)采用响应面法对锥弧型集流器的优化结果显示,集流器对离心风机的声功率级的影响不明显,对气动性能的影响显著;锥弧型集流器的扩张角、收缩角对离心风机的气动性能的影响明显,扩张段长度的影响则很小。

(3)优化后离心风机的效率提高了3.6%,静压提高了4.1%,总压提高了3.9%,声功率级降低了1.7 dB。

[1] 李庆宜. 通风机 [M]. 北京: 机械工业出版社, 1981: 61-64.

[2] KIND R J, TOBIN M G. Flow in a centrifugal fan of the squirrel-cage type [J]. ASME Journal of Turbomachinery, 1990, 112(1): 84-90.

[3] KIND R J. Prediction of flow behavior and performance of squirrel-cage centrifugal fans operating at medium and high flow rates [J]. ASME Journal of Fluids Engineering, 1997, 119(3): 639-646.

[4] MINER S M. Evaluation of blade passage analysis using coarse grids [J]. ASME Journal of Fluids Engineering, 2000, 122(2): 345-348.

[5] LIN S, HUANG C. An integrated experimental and numerical study of forward-curved centrifugal fan [J]. Experimental Thermal and Fluid Science, 2002, 26(5): 421-434.

[6] RAFAEL B, FRANCISCO G, SANDRA V. Numerical model for the unsteady flow features of a squirrel cage fan [C]∥Proceedings of the ASME Fluids Engineering Division Summer Meeting. New York, USA: ASME, 2009: 173-183.

[7] MONTAZERIN N, DAMANGIR A, MIRIAN S. A new concept for squirrel-cage fan inlet [J]. Proceedings of the Institution of Mechanical Engineers: Part A Journal of Power and Energy, 1998, 212(5): 343-349.

[8] MONTAZERIN N, DAMANGIR A, MIRIAN S. Inlet induced flow in squirrel-cage fans [J]. Proceedings of the Institution of Mechanical Engineers: Part A Journal of Power and Energy, 2000, 214(3): 243-253.

[9] 温选锋, 杨昕, 祁大同, 等. 椭圆形进口集流器对多翼离心风机性能影响的实验研究 [J]. 西安交通大学学报, 2011, 45(11): 45-51. WEN Xuanfeng, YANG Xi, QI Datong, et al. Experimental study on the effect of elliptical inlet nozzle on performance of multi-blade centrifugal fan [J]. Journal of Xi’an Jiaotong University, 2011, 45(11): 45-51.

[10]许文明, 郑祖义, 万忠民, 等. 空调柜机多翼离心风机集流器的优化研究 [J]. 制冷学报, 2012, 33(3): 58-61. XU Wenming, ZHENG Zuyi, WAN Zhongmin, et al. Optimization study of bell mouth on multi-blade centrifugal fan used in floor standing air-conditioner [J]. Journal of Refrigeration, 2012, 33(3): 58-61.

[11]杨昕, 温选锋, 袁民建, 等. 双吸多翼离心风机进口集流器偏心安装的试验研究 [J]. 流体机械, 2012, 40(2): 1-4. YANG Xi, WEN Xuanfeng, YUAN Minjian, et al. Experimental research on eccentric inlet of a multi-blade centrifugal fan with dual inlet [J]. Fluid Machinery, 2012, 40(2): 1-4.

[12]王嘉冰, 区颖达, 吴克启. 空调风机叶道内旋涡流动分析及进气口偏心的影响 [J]. 工程热物理学报, 2005, 26(6): 53-55. WANG Jiabin, QU Yinda, WU Keqi. Analysis on the vortices flow in the blade passages of the fan for air-conditioner and the influence of the eccentric fan inlet [J]. Journal of Engineering Thermophysics, 2005, 26(6): 53-55.

[13]Technical Committee ISO/TC 43, Acoustics, Subcommittee SC 1, Noise. ISO3745-2012 Acoustics-determination of sound power levels and sound energy levels of noise sources using sound pressure: precision methods for anechoic rooms and hemi-anechoic rooms [S]. Geneva, Switzerland: ISO, 2012.

[14]国家技术监督局. GB/T 1236-2000 工业通风机用标准化风道进行性能试验 [S]. 北京: 中国标准出版社, 2000.

(编辑 苗凌)

Optimization Design of Centrifugal Fan Inlet Collector by Response Surface Methodology

ZHAO Yanjie1,TAN Junfei2,DANG Feilong1,LI Jingyin1

(1. School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2. CISDI Engineering Co., Ltd., Chongqing 400013, China)

Optimization design method for the inlet collector of a centrifugal fan with high-efficiency and low-noise is investigated. The aerodynamic performances of the centrifugal fan are obtained by numerical simulation in the original parametric design, including the divergence angle and shrinking angle of the fan inlet collector, and the length of the divergent section. The numerical calculation is compared with the experimental result to validate the accuracy of the algorithm. To improve the aerodynamic and acoustic performances of the centrifugal fan, quadratic polynomial regression is considered to analyze the function relation of the centrifugal fan performance and the fan inlet collector parameters, and the optimal structure parameters of centrifugal fan inlet collector are obtained. The results indicate that the three fan inlet collector parameters exert remarkable effects on the aerodynamic performances, but slight effect on sound power level. The divergence angle and shrinking angle of the fan inlet collector obviously affect the aerodynamic performances, while divergent section length does not. After optimizing the centrifugal fan inlet collector, the efficiency and static pressure ratio increase by 3.6% and 4.1%, respectively, and the sound power level decreases by 1.7 dB.

centrifugal fan; inlet collector; response surface methodology; sound power level

2015-02-09。

赵燕杰(1986—),男,博士生;李景银(通信作者),男,教授,博士生导师。

国家自然科学基金资助项目(51276137);中央高校基本科研业务费专项资金资助项目。

时间:2015-08-13

10.7652/xjtuxb201511009

TH432

A

0253-987X(2015)11-0049-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150813.1014.006.html