突发事故救援资源选址优化模型研究

陈桂园，程乃伟沈阳航空航天大学，辽宁沈阳　110136

突发事故救援资源选址优化模型研究

陈桂园，程乃伟
沈阳航空航天大学，辽宁沈阳110136

摘要突发事故救援资源的合理优化对突发事故的应急救援的实施影响巨大，本文通过应用集合覆盖模型（LSCP）以及最大覆盖模型（MCLP）对应急救援资源选址优化进行了分析，得出在经济条件和救援情况双重约束下的最佳选址方案，其结果对有效缩短救援时间减少人员伤亡和财产损失具有重大的意义。

关键词救援资源；选址优化；覆盖模型

0　引言

在突发事故发生后，应急救援需要从外围无数个救援点向内围中心一个或几个需求点输送量相应救援物资和救援人员，进而形成一个集聚性的输送网络。应急救援资源的突发性和不确定性，使得救援点各自为战，应急救援流量、流速、流向失序，救援出现紊乱，使救援工作出现短板效应，严重影响救援工作效率。为了使应急救援能够及时高效的进行，应急救援资源的合理选址和充分储备具有非常重要的意义。

本文根据应急救援资源需求特性，在没有发生突发事故的情况下，在救援点的选址问题上建立应急救援资源优化模型，运用覆盖模型的算法，首先运用LSCP对区域全覆盖选址最小化进行计算，而后运用MCLP计算每个应急救援点对目标区域的覆盖情况，进而选择出在经济和覆盖状况两个条件下的最优方案。

1　应急救援优化覆盖模型

1.1覆盖模型理论

覆盖的定义：对每个需求点设定一个最大标准距离S（或者最大标准时间R），当需求点i至候选救援点j的行车距离（或者行车时间）在设定最大标准距离点S（或者最大标准时间R）之内时，则规定候选救援点j覆盖需求点i。

LSCP是用于确定所需应急救援资源储备点的最少数目，并配置应急救援资源使所有的需求点都能被覆盖到，也就是说对于任何应急地点发生事故，都能有应急服务点到达应急点的距离小于或等于一个规定的值（或者时间小于或等于一个规定的值）。

设二元值决策变量xj，当候选救援点j被选中时，

xj=1；否则，xj=0。

所有需求点的集合为I={i}

全部需求点都能被覆盖到所必须的最少救援点个数和位置可由以下集合覆盖模型确定：

其中，目标函数（1）是设置的救援点数最小，约束条件（2）保证每个需求点至少被一个应急救援点覆盖，约束条件（3）表示决策变量xj为只能取0或者1。

MCLP在给定救援点数量、特定距离条件下，最大化满足被需求点的需求，该模型不需要把所有的需求点都覆盖到，而是确定p个应急救援资源储备点，使在规定的距离或时间内，覆盖尽可能多的人口或最大风险。

设yi是二元值变量，当第i需求点被覆盖时，yi=1；否则，yi=0

最大覆盖模型为：

其中，限制条件中公式（5）确定所选择的救援点数为p，公式（6）保证选定的救援点能够覆盖需求点i，公式（7）限制决策变量xj和yi为(0，l)整数变量。目标函数公式（4）使被覆盖的需求点能有最大的价值，当目标函数（4）中的权数wi都取1时，表示该模型是保证覆盖最多的需求点；当权数wi取值为需求点i的风险程度的综合权重值时，表示该模型是保证救援目标价值最大化。

1.2优化模型仿真算例

以某地区的7个区域为例(1—7)，在4个候选救援点 (A，B，C，D)中选择应急救援资源储备点，每个救援点的覆盖距离为8千米，设置每个区域需求点都在区域的中心位置，4个候选救援点到7个区域中心的行车距离、各区域风险权重值、7个区域的人口如表1所示，这里以每个区域的人口和该区域的风险权重所得综合权重作为该区域的权重，即取wi=第i需求区域的人口数´区域的风险权重值。

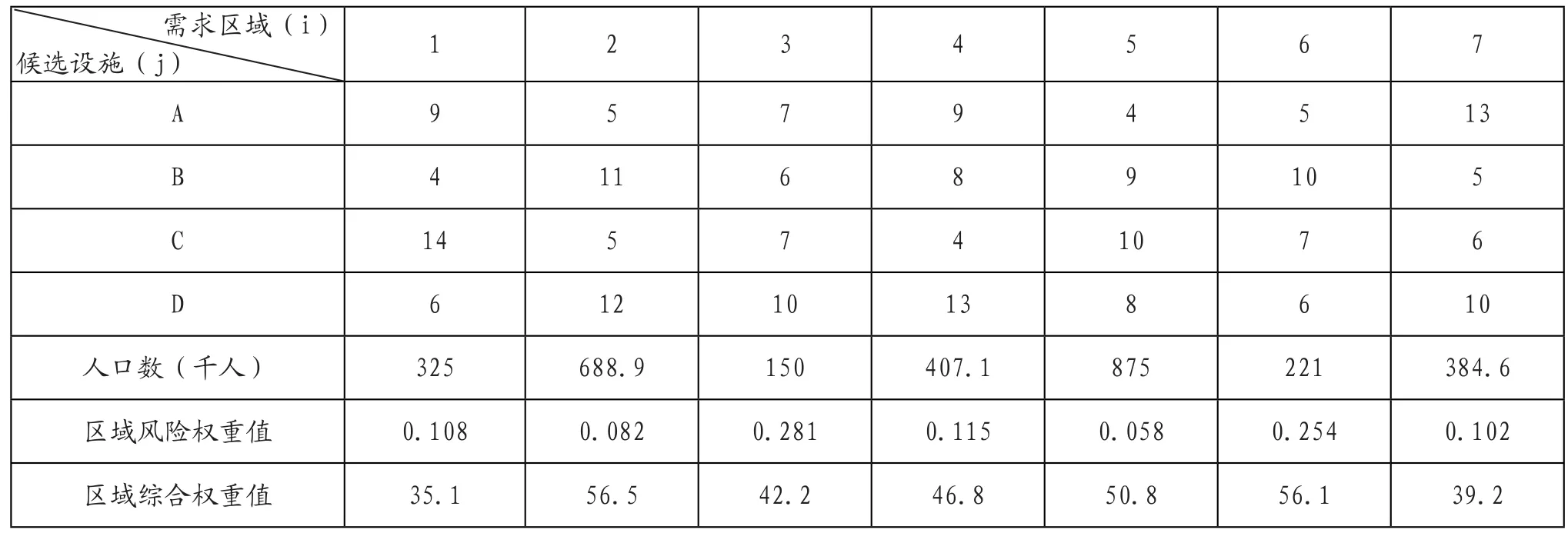
表1　候选救援点到区域中心的行车距离、区域人口及风险权重值

使用LSCP模型：

用MATLAB求最优解为z =3,x1=x2=x3=1，即：要达到覆盖所有需求点，必须在候选救援点A、B和C三个点各设置一个应急救援资源储备点，该模型存在多个最优解，例如，x1+x3+x4³1，也是最优解，这里只针对一组最优解来进行分析。

使用MCLP模型，并使p从1连续增大到3：

当p=1时，解为 x3=1，y2=y3=y4=y6=y7=1，z=240.8，即在候选救援点C设置一个应急救援资源储备点，该救援点能覆盖需求点2、3、4、6和7，覆盖综合值为240.8。

当p = 2时，解为x1=x3=1，y2=y3=y4=y5=y6=y7=1，z=291.6即在候选救援点A和B各设置一个应急救援资源储备点，该救援点能覆盖需求点2、3、4、5、6和7，覆盖综合权重值最大为291.6。

当p=3时，解为：x1=x2=x3=1，z =326.7，yi=1，(i =1,2,3...7)，即在候选救援点A、B和C各设置一个应急救援资源储备点，这三个救援点能覆盖所有需求点，覆盖综合权重值最大为326.7。

从上述的分析结果可以看出，第三个救援点建立后，只在原有的的基础上比原来增大了35.1综合权重值，与前两个救援点相比，第三个救援点不符合经济节约的要求，因为前两个救援点已经覆盖了85.7%，当突发事故发生时，前两个救援点可以对绝大多数区域进行应急救援，所以该区域最佳方案为选择两个应急救援点，分别为A、C救援点。

2　结论

经本文分析验证可知运用LSCP可对区域全覆盖选址最小化进行计算，而后再运用MCLP计算每个应急救援点对目标区域的覆盖情况，将两者结合起来可以选择出在经济和覆盖状况两个条件约束下的最优选址方案，使整个应急救援网络有效发挥作用，彻底改变过去突发事故发生后，主要依靠各级政府临时组织进行收集、调运、发放救灾物资的局面，使应急救援有条不紊的进行，能够有效的缩短救援时间，减少人员伤亡和财产损失。

参考文献

[1]周晓猛.突发事故下应急资源优化配置定量模型研究[J].安全与环境学报，2007，7（6）：113-115.

[2]魏汝营.突发公共事件应急资源优化管理研究[D].中南大学，2009.

[3]张晓光.重大事故应急救援资源调配研究[C]//2010（沈阳）国际安全科学与技术学术研讨会论文集.2010：969-973.

[4]徐之恒.地铁突发事件应急救援资源配置研究[D].西安交通大学，2010.

[5]王苏生.基于公共优化原则的多受灾点应急救援资源配置算法[J].运筹与管理，2008，17（3）：16-21.

[6]SydneyC.K.Chu，LisaChu.Amodelingframeworkforhos pitallocationandserviceallocation[J]Internationaltrans actionsinoperationalresearch.2000，7：539-568.

[7]乔洪波.应急物资需求分类及需求量研究[D].北京交通大学，2009.

作者简介：陈桂园，研究生在读，所在院校：沈阳航空航天大学，专业：安全科学与工程，研究方向：虚拟仿真

中图分类号TP39

文献标识码A

文章编号1674-6708（2015）139-0139-02