当代径赛训练计算模型的研究与应用

张展嘉，张 冰，石 悦，王 悦，郑 尉，王 雄



当代径赛训练计算模型的研究与应用

张展嘉，张 冰，石 悦，王 悦，郑 尉，王 雄

依托现代计算机技术、数学理论及运动生理、生化知识，通过文献资料研究、数学方法和实验法，更新并完善了20世纪70年代的计算训练法理论体系。研究选取恰当的公式模型，并结合专家访谈确定得分公式模型的评分标准及间歇训练负荷标准，然后，通过计算机软件Matlab中lsqcurvefit函数进行公式模型的计算和校对，并代入清华大学田径队运动员的成绩以评估其有效性。最终合理构建成绩得分公式模型和跑步曲线公式模型，更新成绩得分表，囊括23个项目，适用于各个能力水平，并获得了包括总速度表、400 m恒速表和百分比公里速度表的当代新型训练表格，将有效解决“科学评价和计算运动负荷”这一难题。

计算训练法；田径；数学公式模型

1 引言

田径运动是人类历史中最为悠久，对人类生活和社会发展影响较大的体育项目。在竞技体育中，田径运动一直备受人们关注，在竞技场上素有“得田径者得天下”之说[5]。田径运动以周期性项目居多，相对其他技巧性项目而言，其运动强度和量较易控制。但在长期的训练实践过程中，教练员主要依靠经验来评估运动负荷及制定训练计划，人们一直想寻找一种能够评价和计算运动负荷的方法或手段，以减少主观因素的影响，使训练更加科学合理。尽管通过血液、尿液等生理、生化测试可达到此目的，但却始终无法满足既快速无创又方便直接的获得评价结果的需求。

20世纪70年代，美国系统分析专家James B.Gardner以及电子计算机专家J.Gerry Purdy共同出版《计算训练法》一书，首次将数学理论与田径训练实践相结合，用“数学模型”来准确评估和预测运动成绩，并通过各种训练表格来直接指导训练。该书在当时田径领域引发轰动，为众多教练员所追捧，并在其他项目中得到了发展和延伸[1,2,6]，还有学者将其制作成软件用来指导训练[3]。计算训练法作者将数理知识与运动训练经验完美结合，不仅推导出与训练成绩相关的数理公式，还通过计算机生成相应的时间表，帮助教练员制定训练计划，在运动训练中发挥巨大作用。计算训练法生成的时间表种类及各表的功能如表1所示[4]。

表 1 计算训练法表格一览表Table 1 Tables of Computerized Running Training Programs

转眼40多年过去，世界纪录已被无数次刷新，人类平均运动能力有了巨大进步，田径比赛场地、运动员器材(装备)以及比赛规则也都发生了翻天覆地的变化。因此，原计算训练法的公式模型系数已不适合当前的情况，其理论基础也略显青涩和不足。在电子科技高度发展的今天，计算机辅助训练的方法以其精确、实用、快捷、科学的特点深受广大教练员及体育爱好者的喜爱，结合高新技术对田径训练领域进行全面、深入的介入已势在必行。因此，应用现代最新数学理论以及生理生化知识完善计算训练法理论体系，并通过计算机更新所有表格，使其符合当今田径训练的特点，这不仅对我国田径运动员整体成绩水平的提高有帮助，更能满足众多体育爱好者提升自身运动能力的渴望。

2 研究方法

2.1 文献资料研究

本研究通过查阅文献，梳理计算训练法相关的研究，选取恰当的公式模型，并结合专家访谈确定得分公式模型的评分标准及总速度表中间歇训练负荷标准，其中，样本数据通过IAAF官方网站获得。

2.2 数学方法

各公式模型的计算是通过数学方法实现的。对标准径赛距离的得分标准成绩，套用Purdy得分公式模型，利用非线性拟合法得到归一化得分公式；非标准径赛距离的得分标准成绩可通过跑步曲线公式模型和局部线性回归或局部二次回归得到，再利用Purdy 得分公式模型得到非标准径赛距离的归一化得分公式。所有公式中的待定参数都可通过非线性拟合法得到，具体计算利用Matlab中的lsqcurvefit函数实现，并通过SPSS 20.0对误差进行验证。

2.3 实验法

在初步获得成绩得分表之后，本研究选取清华大学高水平田径队19名运动员为测试对象，搜集其比赛成绩及同期各个训练距离的成绩，对新的训练表格进行评估，以验证表格有效性。

3 新成绩得分表理论构建基础及得分公式模型确立

3.1 新成绩得分表构建指导原则

以Purdy和国际田联分别制定的得分表构建指导原则为基础，本研究希望整合二者的优势，从评价更精确和更利于训练的角度制定了指导原则：

1.定义性原则：新生成的得分表中，每1分都代表1个运动成绩单位，以达到用得分来衡量不同项目运动成绩的目的。

2.递增性原则：分数要随着运动成绩的提高而提高。

3.对等性原则：每一项目，在难度和运动成绩相当的情况下，得到的分数也应相同。

4.特异性原则：不同运动项目，其运动成绩的最高值和最低值也不同。

5.同源性原则：不同性别，其得分评价标准也不尽相同，因此，男、女运动员得分标准需分别制定。

6.零分原则：本研究的0分标准低于国际田联，且因项目而定，沿用Purdy的标准，对不同径赛项目的0分定义如下：人类在疲劳恢复充分和能量供应充足的情况下，能够无限走下去的速度为Z=2-d/99950 m/s(d为距离)。需要说明的是，成绩为0分并不代表能力为零。

7.累进性原则：随着运动水平的进步，提高运动成绩的难度逐渐增大，分数也越难提高。因此，提高同样的成绩，运动员的运动水平越高，其分值增加幅度也越大。

8.数学上的一致性：对于任何一个项目，随着运动成绩的提高，其分数水平呈递增趋势，相邻2个运动成绩的差值应是不变或递增的。

3.2 得分表公式模型的确立及标准径赛距离得分表的生成

通过比较分析历史上影响力较大的成绩得分公式模型，本研究从实证性和实用性角度出发，采用1975年Purdy创造的得分公式模型。在完全掌握Purdy公式模型的基础上，重现作者当年的得分表，且偏差控制在4分以内。希望在此基础上进行深入研究，套用当今径赛成绩以更新其公式系数，并通过后期的校对评估增强系数的稳定性，使新的成绩得分表能够有效评估运动员的真实水平。

1975年Purdy得分公式模型为：

P=C1(M-z)+C2(eC3(M-z)-1)

其中，P代表得分；M代表运动成绩，也可用速度V(m/s)或距离d(m)表示；Z为0分成绩[Z=2-d/99950m/s(d为距离)]；C1、C2、C3为不同项目所特有的系数。由于公式中存在3个未知系数，因此，需设定至少3个得分标准及其相应成绩才可获得系数，而得分标准的确定应具备能够合理区别不同运动等级的特点，即优异(Excellent)—1 400分、优秀(Good)—1 100分、一般(Ordinary)—500分。本研究依照当今径赛成绩的发展趋势，重新界定了各个评分标准所对应的运动成绩(表2)。

科学选取各个评分标准所对应的成绩是生成系数的前提。为了保证所选样本数据的合理性，并排除偶然性因素的影响，本研究对于不同评分标准的样本数据选取如表3所示。

表 2 本研究得分公式模型的评分标准一览表Table 2 Scoring Standard of Scoring Formula Model

表 3 本研究得分公式模型评分标准的选取一览表Table 3 Selection of Scoring Standard of Scoring Formula Model

注：数据源自国际田联官方网站http://www.iaaf.org/statistics/toplists/index.html，以及WMA(世界大师赛)官方网站http://www.world-masters-athletics.org/records。

将所有国际田联认可的标准径赛项目(接力、跨栏、障碍、竞走除外共15项)的相关成绩收集整理好之后，即可生成各标准径赛项目得分公式模型的系数。为尽量减少不稳定函数的影响，本研究采用归一化方法，即将500分、1 100分、1 400分和0分的运动成绩除以1 400分运动成绩所得的百分比作为自变量带入得分公式，然后，通过调用Levenberg-Marquardt算法，求解与Purdy III[7]中相同的非线性最小二乘法问题来确定系数C1、C2、C3。

获得新的公式系数之后，需对其进行多次校对以保证模型合理性。为了使成绩得分表能够更好的反映运动员的实际运动能力，本研究设计了一种循环校对程序以获得更恰当的成绩得分公式：对两个距离相近的比赛项目，如100 m和200 m项目，首先，利用两组得分标准运动成绩，按之前所述方法可得到各自的初始归一化得分公式；之后，分析同一运动员在两得分公式中的得分偏差，再取所有得分偏差的绝对值平均数；最后，寻找合适的得分标准成绩组合以使得相应的分数偏差绝对值平均数最小。假设校对数据能充分反映同一水平运动员在不同项目下的运动水平，循环校对可实现相邻距离比赛项目间相同运动水平成绩的可比性。

对于多个相邻径赛距离项目得分公式的确定，可先利用上述过程求得两个项目的得分公式，再以此为基准，通过循环校对过程得到其余项目的得分公式。至此，通过循环校对过程即可得到所有标准比赛距离得分公式。通过循环校对程序的校对之后，新的标准径赛距离得分公式模型的系数如表4所示。

表 4 本研究标准径赛距离得分公式模型系数一览表Table 4 Coefficients of Standard Running Distances Scoring Formula Model

在对所有项目得分公式系数校对完毕之后，统计分析各个项目的实际成绩与推测成绩的偏差(表5)。结果表明，短跑项目除400 m外，误差控制在0.25 s之内，中长跑项目(800～1 500 m)误差控制3～6 s之内，长跑项目(1英里～马拉松)误差控制在5～20 s之内。其中，1英里和10 000 m误差较大，最高达到8 s和16 s，这可能是由于在推算过程中二者前后项目距离差距过大所致，理论上，距离间隔越近，曲线推测的精确度也会越高。对男、女各个项目推测成绩与实际成绩进行独立样本t检验的结果显示，所有项目P值均大于0.05，无显著性差异。综上研究证实，新成绩得分表能够很好反映运动员的真实运动能力。

在获得了各项标准径赛距离得分公式模型系数之后，通过Matlab即可生成各个项目的成绩得分表，例表如表6所示。

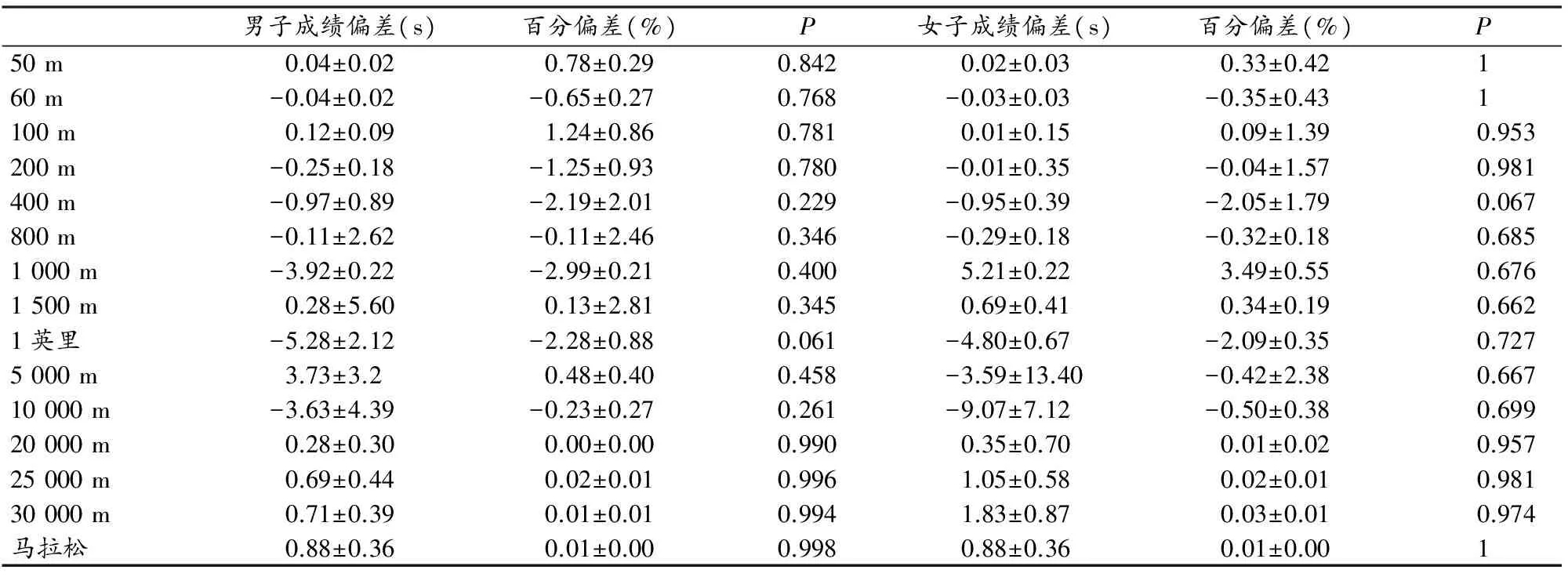
表 5 本研究各项目成绩偏差(实际成绩-推测成绩)及百分偏差比较一览表Table 5 Comparison of Performance Deviation (Real Performance - Anticipated Performance) (in seconds) and Percentage Deviation

表 6 本研究新标准径赛距离部分成绩得分表样表(男子为例)一览表Table 6 Samples of New Standard Running Distances Scoring Table (Male)

注：对于给定的分数，某些项目可能没有直接对应的运动成绩，此时运动成绩选取该得分以下且最接近该分的运动成绩。

4 非标准径赛距离成绩得分表的生成

通过对已有标准径赛距离项目的成绩用标点法画出的跑步曲线，其最大意义在于可以精确推测其非标准径赛距离项目的成绩。本研究通过对历史上较为著名的跑步曲线公式模型进行梳理分析，最终打算采用1974年Purdy基于Henry模型推导出的公式模型，并通过曲线拟合技术画出2011年男子世界纪录成绩的跑步曲线，且偏差控制在合理范围之内。

1974年Purdy的跑步曲线公式模型为：

V=-b1e-r1d+b2e-r2d+b3e-r3d+b4e-r4d+b5e-r5d

模型中各指数项代表的生理意义：第1指数项：从起跑至加速至最大速度V过程中的负加速度，故为负指数项，代表人体克服内部阻力和加速过程中造成的动量损失。第2指数项：短跑过程中产生的非乳酸性氧债。第3指数项：乳酸性氧债，在30 s和215 s的半时消耗中分别提供30 kcal和90 kcal的能量。第4指数项：糖原消耗，或有氧跑步(稳定期)时的基础供能，Henry模型中糖原储存的半衰期为3.27 h。第5指数项：其他代谢影响因素，如脂肪代谢，其半衰期为6.5天。在重现作者当年跑步曲线公式模型的基础上，本研究采用当今世界成绩生成新的跑步曲线公式系数，以达到适应现代田径运动成绩发展趋势的目的。

对于非标准径赛距离得分表的生成，同样需要3个得分标准，即1 400分、1 100分和500分，以及相对应的成绩。标准距离的得分标准成绩可通过现有数据查到，而对于非标准距离而言，因无现成数据可供参考，其得分公式的生成相对而言较为复杂。根据Purdy的跑步曲线模型，利用标准距离的1 400分成绩来推算非标准径赛距离的得分标准成绩：利用已经校验过的标准径赛距离的得分标准成绩，得到跑步曲线公式，从而可得到非标准径赛距离的1 400分标准成绩。而1 100分和500分运动成绩不能应用跑步曲线，因为跑步曲线是用来刻画世界最好运动水平的公式。1 100分和500分运动成绩的确定，是通过对标准距离的运动成绩做局部线性回归或者二次回归得到的。之后，进一步利用得分表公式模型可求得归一化得分公式。通过计算获得非标准径赛得分表公式系数，其项目名称及相应系数如表7所示。

在获得成绩得分表之后，需要验证其在实际训练中的准确性。本研究以清华大学高水平运动队10名短跑运动员(2名国际健将，5名国家健将，3名国家一级)和9名长跑运动员(1名国家健将，8名国家一级)同一时期的比赛和训练成绩为评估参考样本，基于运动员主项成绩推测其翼项项目成绩，分析实际成绩与推测成绩误差，以评估其有效性(表8、表9)。

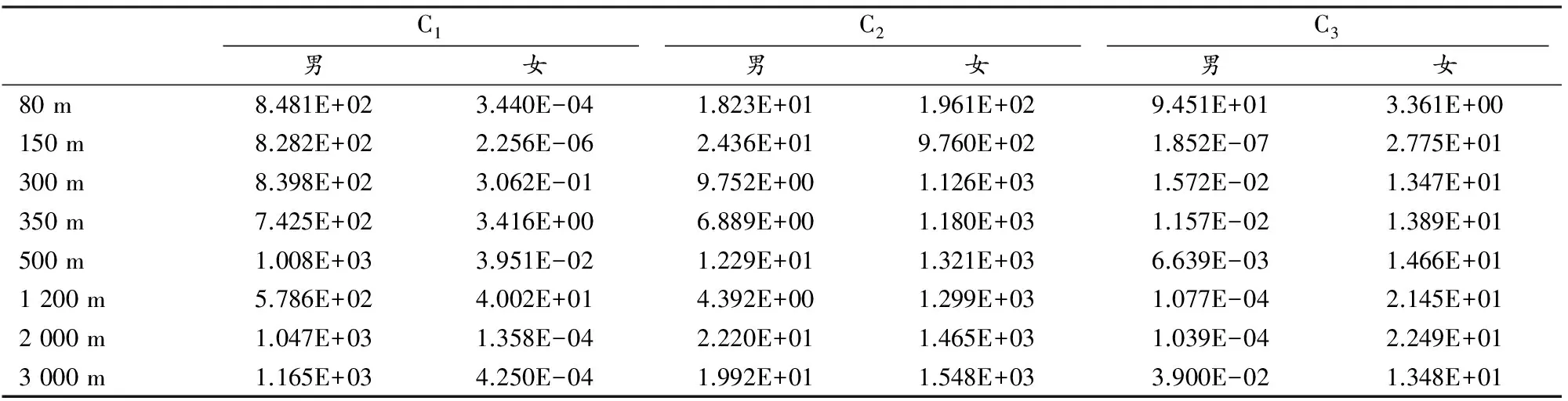
表 7 本研究非标准径赛距离得分公式模型系数一览表Table 7 Coefficients of Non-Standard Running Distances Scoring Formula Model

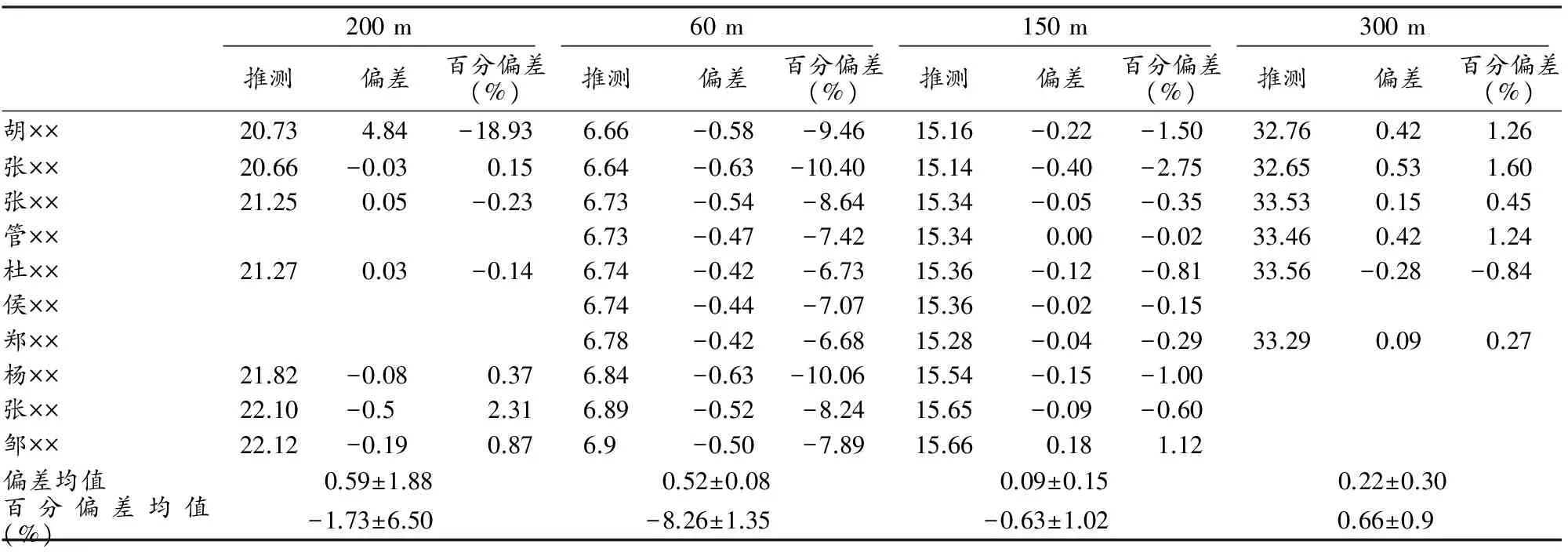
表 8 清华大学田径队短跑运动员推测翼项成绩及其偏差(实际成绩-推测成绩)一览表Table 8 Anticipated Performance and Deviation (Real Performance-Anticipated Performance) (in seconds) of Short Distance Atheles from Tsinghua Univeristy (s)

表 9 清华大学田径队中长跑运动员推测翼项成绩及其偏差(实际成绩-推测成绩)一览表Table 9 Anticipated Performance and Deviation (Real Performance-Anticipated Performance)(in seconds) of Middle and Long Distance Atheles from Tsinghua Univeristy (s)

注：本研究搜集到的翼项成绩数据为手动计时成绩，为方便比较分析，将手动计时成绩换算为电计时成绩。手动计时与电计时关系：同一运动员某项目的电计时成绩=手动计时成绩×(1+0.24%)。

由表9可知，对于短跑项目而言，评估效果大体良好，平均偏差控制在0.6 s以内。胡××的200 m成绩推测值明显偏高，原因为对于国际水平的运动员而言，由于训练距离及侧重发展的能力素质等因素，导致其100 m专项能力过于突出，没有完全挖掘其200 m潜能，使其在200 m项目上未能达到与100 m专项能力相当的运动水平。此外，所有运动员的60 m实际成绩均低于推测成绩，且平均偏差达到-8.26%，造成这种现象的原因：1)距离越短，手动计时误差对整体成绩的影响越为明显，极易因为较小的计时误差引起较大的成绩偏差；2)对于短跑运动员而言，注重爆发力及力量的训练，但如果速度耐力没有达到同等水平，其在后半程则无法维持前60 m的高效运动，导致其整体专项成绩降低；3)60 m的成绩是基于运动员的专项成绩而推测的，推测成绩高于实际成绩，说明运动员在其专项上还有继续发展的空间。除此以外，其余项目的偏差均控制在合理范围之内。对于长跑项目而言，平均偏差稍高，这是由于运动距离加长所致，偏差百分比控制在合理范围内。本研究认为，随着运动距离的加长，对于运动成绩的精准度要求也可适当放宽。本研究确定了生成得分表所必须的公式模型及各个项目的公式系数，并通过双循环校对程序，获得评估效果良好的标准和非标准径赛距离成绩得分表。经过评估，新成绩得分表已可以较好地评价运动员的运动能力水平，这为后续各种训练表格的生成和使用提供良好的保证。

5 新速度表种类与功能确定

在生成了科学合理的成绩得分表之后，如何在实际运动训练中使用新计算训练法是本研究需要探讨的另一重要问题。“速度表”是计算训练法的核心，也是教练员在实际训练中制定训练计划、了解运动员机能状态的关键。因此，为了便于不同径赛项目的教练员和运动员使用该表，需设立不同种类的速度表，以满足不同训练形式的需要。本研究在原《计算训练法》速度表类型的基础上，依据现代田径运动的训练方式，从实践的角度出发，设立总速度表、400 m恒速表以及百分比公里速度表3种速度表类型。

5.1 总速度表

该表包括15项标准径赛距离和常用8项训练距离(接力、跨栏、障碍、竞走除外)，提供了任意分数水平的运动员在某个专项距离最高速度的百分比成绩以及该速度水平下的运动频率和强度，教练员可参照此表为运动员制定训练计划。对于间歇性训练负荷标准的制定，本研究决定沿用原《计算训练法》所提供的运动负荷标准，该标准为Purdy和Gardner当年总结训练经验，通过众多运动员的训练计划统计得出，具备广泛的适用性。

总速度表的生成方法：首先，给定一分数水平，通过查找成绩得分表得到此分数水平下各项目距离的运动成绩，作为该分数水平对应的最高专项运动成绩。其次，将最高专项运动成绩除以不同百分比所对应的运动成绩。依照上法，即可获得各分数水平下的速度表，表中规定的间歇时间和重复次数可以根据恢复特点、运动员的自我反应和所用的恢复形式进行灵活调整(表10)。

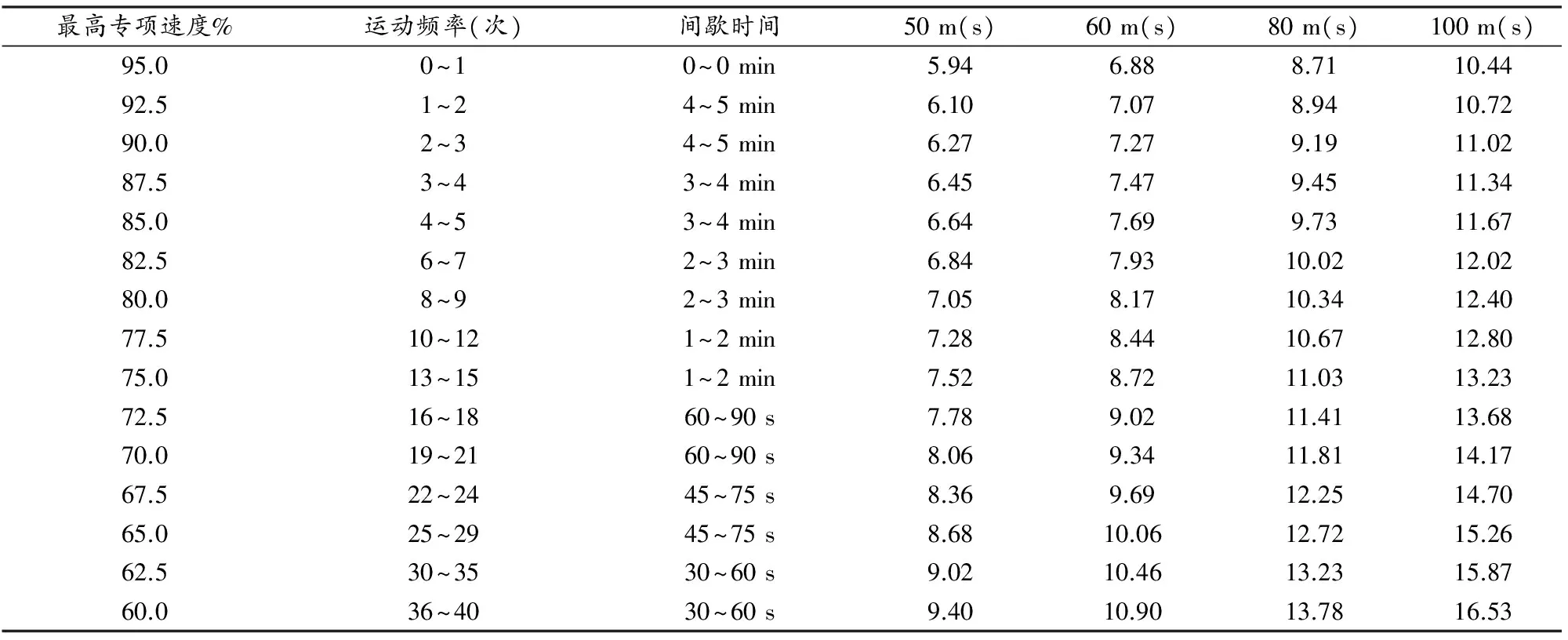
表 10 本研究总速度表样表一览表(男子1 120分为例)Table 10 Samples of Speed Table (Male,Score:1120)

5.2 400 m恒速表

在中长跑训练过程中，教练员常会安排一些间歇训练，按比赛的速度跑一些短于比赛的距离，因此，需要知道跑某种中间距离的速度是多少。例如，希望用2 min跑800 m的速度跑一些300 m的间歇跑。较常用的是以某一比赛距离的速度跑一些400 m(正规径赛跑道一圈)的间歇跑。本研究设计400 m恒速表最左侧一栏为400 m从43 s～1 min36 s成绩，时间间隔为1 s，右侧则对应相同速度(m/s)下其他项目的恒速成绩(s)，共12项。例如，如果运动员跑完400 m的时间是45 s，以此速度跑150 m的时间是：45×(150/400)=16.875 s，300 m的运动时间为45×(300/400)=33.75 s，其他成绩和距离依此类推(表11)。

表 11 本研究400 m恒速表样表一览表Table 11 Samples of 400 m Constant Speed Table

5.3 百分比公里速度表

该表较适合中跑和长跑运动员使用。它以已知的每公里平均成绩为基础，列举出不同百分比速度下的成绩。左边一栏为百分之百用力跑下的每公里成绩(时间范围为2:10.0～5:00.0，时间间隔为1 s)，其余栏为每公里不同百分比速度所对应的运动时间，百分比范围为100%～40%，100%～80%之间间隔为2%，之后为5%。例如，如果运动员全力跑1 km的时间是2 min 14 s(2×60 s+14 s=134 s)，则此运动员以90%的速度跑1 km的时间应该为：134/0.90=148.88 s，即2 min 28.9 s，其他百分比速度对应的运动时间依此类推(表12)。

5.4 各训练表内容及相应功能

如表12所示，全部训练表格生成完成，对各个训练表格中所包含的内容及相应功能进行梳理统计，结果如表13所示。

表 12 本研究百分比公里速度表样表一览表Table 12 Samples of Percentage Kilometer Speed Table

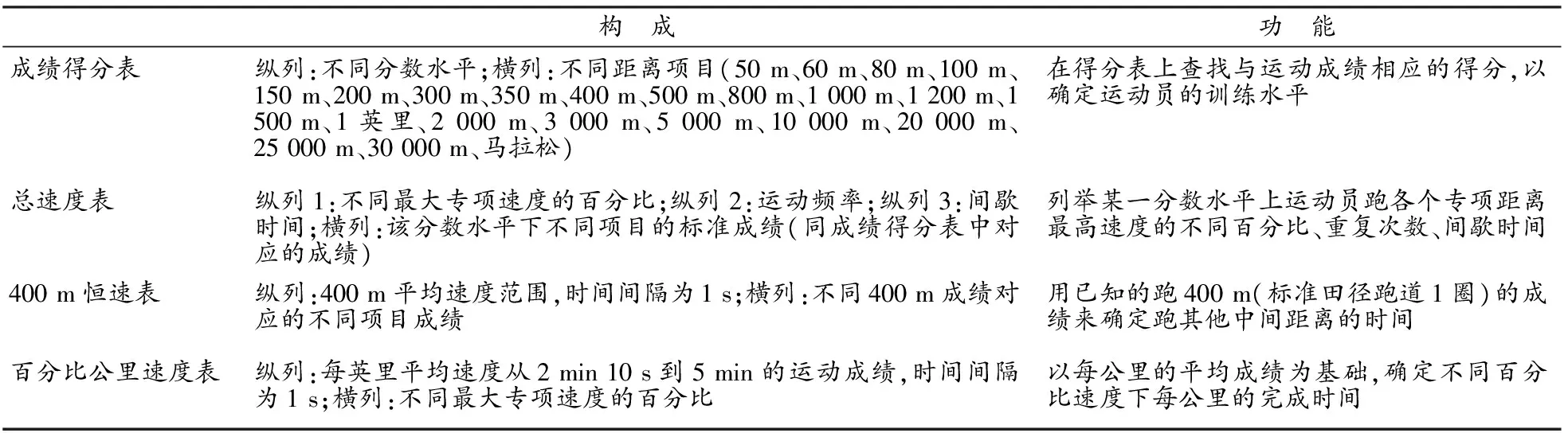
表 13 本研究新训练表格种类及功能一览表Table13 Catagories and Usages of New Training Tables

6 结论与建议

6.1 结论

1.本研究完善计算训练法理论体系，合理构建成绩得分公式模型和跑步曲线公式模型，成功更新成绩得分表，囊括23个项目(标准距离15项，非标准比赛距离8项)，适用于各个能力水平(普通人及专业运动员)。

2.通过循环校对程序，新生成公式模型系数的稳定性得到保证。最终，将短跑项目(50 m～400 m)误差控制在0.1～1 s之内，中长跑项目(800 m～1 500 m)误差控制3～6 s之内，长跑项目(1英里～马拉松)误差控制在8～20 s之内。

3.获得新训练表格：新成绩得分表、总速度表、400 m恒速表、百分比公里速度表。教练员可根据不同专项特点合理使用表格。

6.2 建议

对于公式模型的校对，理论上讲，样本量越大，项目距离越接近，其准确度也会越高。因此，若想进一步完善公式模型，后期研究工作可以继续采集更多的成绩样本，以期获得预测效果更佳的模型。本研究所涉及的项目为跑类项目，并不包括接力、跨栏、障碍、竞走，但理论上讲，计算训练法理论适用于任何周期性项目，历史上也曾有过应用计算训练法指导游泳、速滑、自行车等项目的先例。如果能将本研究成果进行细化和拓展性研究，对其他所有周期性项目的发展具有重大意义。

[1]陈家和.计算训练法在游泳训练中的应用[J].武汉体育学院学报,1988，(1)：40-43.

[2]刘波,袁志华.足球运动员耐力训练运用计算训练法的可行性分析[J].体育世界:学术版,2008,(8):66-67.

[3]王路德.“计算训练法” 软件的研究[J].体育科学,1988,8(3):88-88.

[4]詹姆斯·加德纳,格里·珀迪.计算训练法[M].金嘉纳,沈纯德,译.北京：人民体育出版社，1983.

[5]张贵敏.田径[M].北京:人民体育出版社,2007.

[6]周素英,岳安元.计算训练法在自行车短距离项目训练中的应用[J].山西体育科技,2001,21(1):6-7.

[7]PURDY J G.Computer generated track and field scoring tables:III.Model evaluation and analysis[J].Med Sci Sports,1976,9(4):212-218.

Research and Application of Contemporary Computerized Running Training Programs

ZHANG Zhan-jia,ZHANG Bing,SHI Yue,WANG Yue,ZHENG Wei,WANG Xiong

Based on the modern computer technology,mathematical theory and exercise physiology and biochemistry knowledge,this study used documentary methods,mathematical methods and experimental methods to update and improve the original theoretical system.First,the research chose proper formula models and determined the scoring standard and load standard of intermittent training combined with experts’ interviews.Then the research used lsqcurvefit function in Matlab to calculate “scoring formula” and “running curve formula”,after which the athletes’ performances of Tsinghua University were used to assess the validness.Finally the study built new scoring formula and running curve formula and updated scoring tables successfully,which include 23 items,which could be applied to every athletic level.And new training tables were also formulated including speed table,400m constant speed table and percentage kilometer speed table,by which the problem of assessing and calculating the sports load will be solved effectively.

computerizedrunningtrainingprograms;trackandfield;mathematicalformulamodel

2014-12-10；

2015-04-28

清华大学自主科研计划课题(2011THZ01)。

张展嘉(1991-)，男，浙江人，在读硕士研究生，主要研究方向为运动与健康、运动训练，E-mail:zhang-zj13@mails.tsinghua.edu.cn；张冰(1960-)，男，辽宁人，教授，博士，博士研究生导师，主要研究方向为运动健康管理，Tel；(010)62796932，E-mail:bzhang@mail.tsinghua.edu.cn；石悦(1988-)，女，回族，黑龙江人，硕士，主要研究方向为运动生理学，E-mail:shiyue_tsinghua@126.com；王悦(1992-)，男，湖北人，在读硕士研究生，主要研究方向为体能康复，E-mail:yue-wang14@mails.tsinghua.edu.cn；郑尉(1985-)，女，河北人，在读博士研究生，主要研究方向为体质健康，E-mail:zhengwei1020@126.com；王雄(1984-)，男，安徽人，在读博士研究生，主要研究方向为体能训练和健康促进工程，Tel：(010)87183309，E-mail:wangxiong223@gmail.com。

清华大学 体育部，北京 100084 Tsinghua University,Beijing 100084,China.

1002-9826(2015)04-0021-07

10.16470/j.csst.201504003

G82

A