粉末冶金Fe-2Cu-0.6C齿轮表面滚压致密的有限元模拟与实验研究

罗 奕，滕 浩，李志友，周科朝



粉末冶金Fe-2Cu-0.6C齿轮表面滚压致密的有限元模拟与实验研究

罗 奕，滕 浩，李志友，周科朝

(中南大学粉末冶金国家重点实验室，长沙 410083)

采用Deform-3D软件对相对密度为90%的Fe-2Cu-0.6C粉末冶金齿轮表面滚压过程进行有限元模拟，研究滚压过程中齿轮应力应变和相对密度的分布及变化规律，并利用标准渐开线齿形的工具轮进行齿轮坯料滚压实验来验证有限元模拟结果。模拟结果表明，轮齿两侧面的等效应变分布存在差异，进入滚压面的最大等效应变出现在分度圆附近，退出滚压面的最大等效应变出现在齿顶。齿面上的等效应力随滚压圈数增加而快速增大，并逐渐趋于稳定。齿面表层相对密度的提高可分为3个阶段，分别为孔隙快速压实阶段、密度缓慢增长阶段与密度稳定阶段。工具轮完成0.6 mm的进给后，轮齿表面到心部的相对密度呈梯度分布，表面形成大约0.3~0.5 mm厚度的致密层(相对密度≥98%)。实验结果与模拟结果具有较好的一致性，验证了有限元模型的可靠性。

粉末冶金齿轮；表面致密；有限元；Deform-3D

随着粉末冶金零件在汽车零部件制造领域的广泛应用，高密度和高性能粉末冶金零件的市场需求量越来越大，如变速器齿轮、同步器齿毂和齿套等[1]。采用一次压制烧结方法生产的粉末冶金齿轮密度一般低于7.2 g/cm3，孔隙率高于8%，抗疲劳强度约为普通锻钢齿轮的60%[2]。粉末锻造是提高粉末冶金齿轮材料密度的常用方法，可将齿轮整体孔隙度减小到接近零，但其尺寸精度差，成本高。采用表面滚压工艺可使粉末冶金齿轮轮齿的表面产生一定厚度的致密层，提高齿轮的接触疲劳与弯曲疲劳寿命，同时心部仍然保持初始相对密度，有利于减轻齿轮质量和减振降噪，并且表面滚压烧结齿轮的生产成本比锻钢齿轮的生产成本低30%左右[3−5]。

表面滚压的致密效果受多种因素影响，如滚压进给量、材料的塑性性能以及齿轮坯料的余量等，通过实验研究各参数对滚压结果影响的成本高、工作量 大[6]。采用有限元技术进行仿真易于操作，可为调整滚压模型和优化滚压工艺提供一种可行的途径。KLOKE等[7]利用有限元软件SFTC-DEFORMTM，对Fe-Ni-Cu-Mo-C烧结齿轮滚压致密过程进行仿真，发现致密层厚度随滚压力、初始相对密度和滚压圈数的增加而增加，但达到一定厚度时不再发生变化。PLANITZER等[8]采用Gurson-Tvergaard型本构方程，通过有限元软件(Abaqus)对齿轮二维平面模型进行径向滚压致密研究，发现滚压后坯料齿形发生明显变化，轮齿上各处的致密效果存在不均匀性。YAZICI等[9]通过建立多孔材料的Gologanu型本构关系研究滚压过程，结果表明同一轮齿左右两侧的应力状态存在差异，且滚压后坯料齿形精度主要受工具轮齿形控制。目前文献报道的滚压仿真大多集中于考察滚压后的致密效果，对于滚压过程中齿轮的塑性变形研究较少，而且模拟时常采用软件自带的材料本构关系，降低了计算精度[10−11]。Deform-3D是用于各种金属及粉末烧结体材料成形工艺的模拟仿真软件，界面友好、操作方便简单[12]。本文作者采用有限元软件Deform-3D对Fe-2Cu-0.6C粉末冶金齿轮滚压致密的三维模型进行仿真，以材料的真应力−真应变曲线定义其本构关系，重点分析滚压过程中的应力、应变和相对密度的分布及变化规律，为表面致密化工艺的深入研究提供指导，并对有限元结果进行相应的实验验证。

1 有限元模型的建立

1.1 仿真几何模型建立及网格划分

渐开线齿轮坯料的齿数为21、齿宽10 mm、模数2 mm，工具轮齿数73、齿宽30 mm、模数2 mm。二者的实体模型均由Solidworks建立，然后导入DEFROM-3D中进行网格划分。为减少计算时间与提高计算精度，对坯料的部分轮齿进行网格化细分，工具轮视为不变形刚体，不划分网格。滚压模型及追踪节点的选取如图1所示，其中P1、P2、P3、P4、P5点分别距离轮廓表面0、0.2、0.5、0.7和1.5 mm，P6、P7点分别位于齿顶与齿根部。

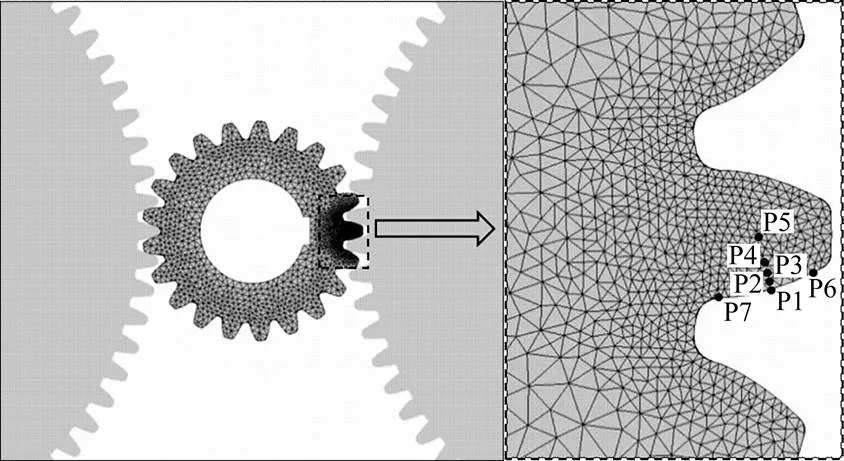
图1 滚压模型示意图及追踪点选取

1.2 应力−应变曲线

仿真时为了描述粉末冶金齿轮坯料的塑性变形行为，需要获得齿轮材料在全致密状态下的真应力−真应变曲线[13]。本研究所选用的材料为Fe-2Cu-0.6C，按其名义成分称量Fe粉、Cu粉、C粉，添加0.6%的硬脂酸锌作为润滑剂，混合均匀后在室温下压制成直径20 mm、高20 mm的圆柱形压坯，在1 120 ℃进行烧结，采用排水法测得烧结样品的密度为7.010 g/cm3(相对密度约90%)。为了获得全致密的样品，对烧结后的样品进行自由锻，锻后再次烧结。通过线切割在合金样品中心取出直径为6 mm、长度为9 mm的小圆柱体，测得小圆柱体的密度为7.785 g/cm3(相对密度约99.8%)，视作全致密。对小圆柱体进行压缩实验，得到材料的真应力–真应变曲线，如图2所示，将真应力–真应变曲线以数据点形式导入软件。定义材料的初始相对密度=0.9，弹性模量=13.5×105MPa，泊松比=0.3。

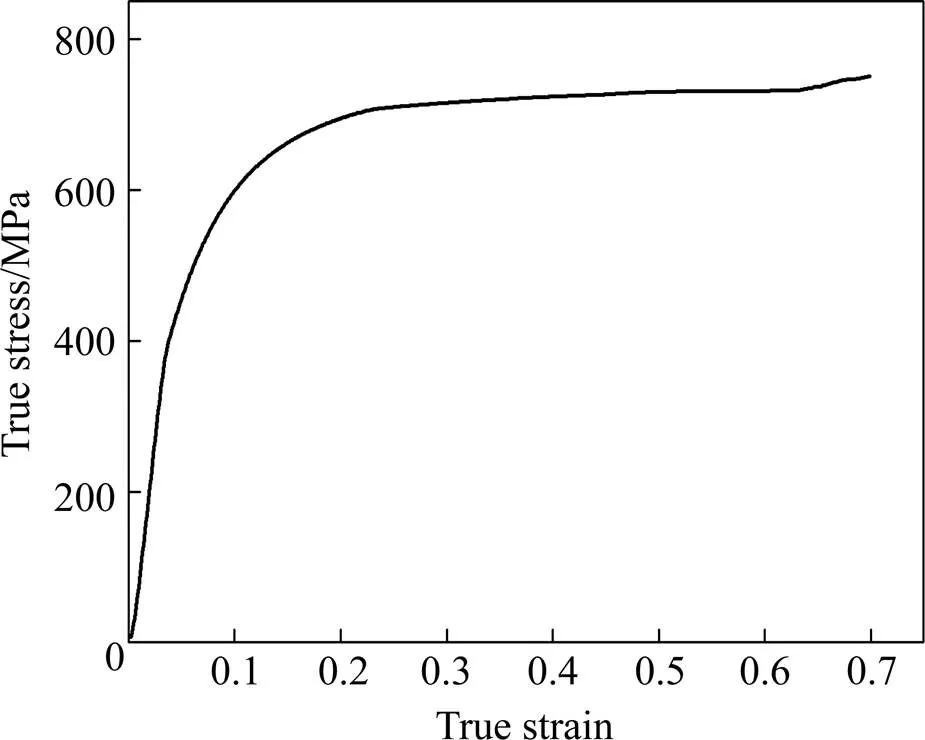
图2 Fe-2Cu-0.6C材料的真应力–真应变曲线

1.3 模型参数设置

实际加工时，齿轮的表面滚压致密过程可分为3个阶段，初始阶段工具轮与齿轮坯料在旋转中接触并相互咬合；第2阶段工具轮沿与旋转轴垂直方向(横向)进给对齿轮坯料加载，直到两轮达到预设中心距；最后阶段工具轮旋转退出。为了减少计算时间，仿真时做一定的简化，模拟采取的工况为：工具轮在初始位置旋转并横向进给，达到预定进给量后工具轮保持在此位置继续旋转一周，模拟结束。

模拟计算时，只保留齿轮坯料在Z轴(旋转中心轴)的自由度。工具轮的旋转速度设为25 r/min，旋转一周的时间为2.4 s，沿X轴(横向)的进给速度列于表1。工具轮与坯料之间的摩擦条件采用剪切摩擦模型，摩擦因数设为0.08。

表1 滚压过程中工具齿轮的横向进给速度及进给量

2 模拟结果与分析

2.1 应变场

图3所示为滚压过程中轮齿的等效应变分布云图。图中从step10到step80、step80到step160分别为滚压过程的初期和中期，step160到step240为滚压后期。滚压开始时等效应变主要集中于齿顶附近(见图3 step10)，随着滚压进行，齿面上等效应变开始增大，应变分布变得复杂且不均匀。这一现象是由齿轮啮合特点所决定的，一对齿廓啮合时，最初是齿轮坯料的齿顶部分与工具轮的齿根部分相接触，随着两轮继续传动，坯料上的啮合位置由齿顶向齿根移动，坯料变形区也随之变化。齿端面的应变分布变化显示，滚压过程中材料的塑性流动主要集中在轮齿表层一定深度范围内，轮齿心部基本不发生变形。完成7.2 s滚压后，整个轮齿的平均等效应变为1.2。

图4(a)所示为齿轮啮合时的接触状态示意图。工具轮逆时针旋转，带动齿轮坯料顺时针旋转，在这一旋转方向下坯料齿廓上的I面为进入滚压面，II面为退出滚压面[13]。由于这2个面受力状态不一样，引起塑性流变行为存在差异，从而导致相应的应变分布不一致。图4(b)所示的滚压结束时轮齿两侧面上的等效应变分布云图证实进入滚压面和退出滚压面上的等效应变分布存在较大差异。

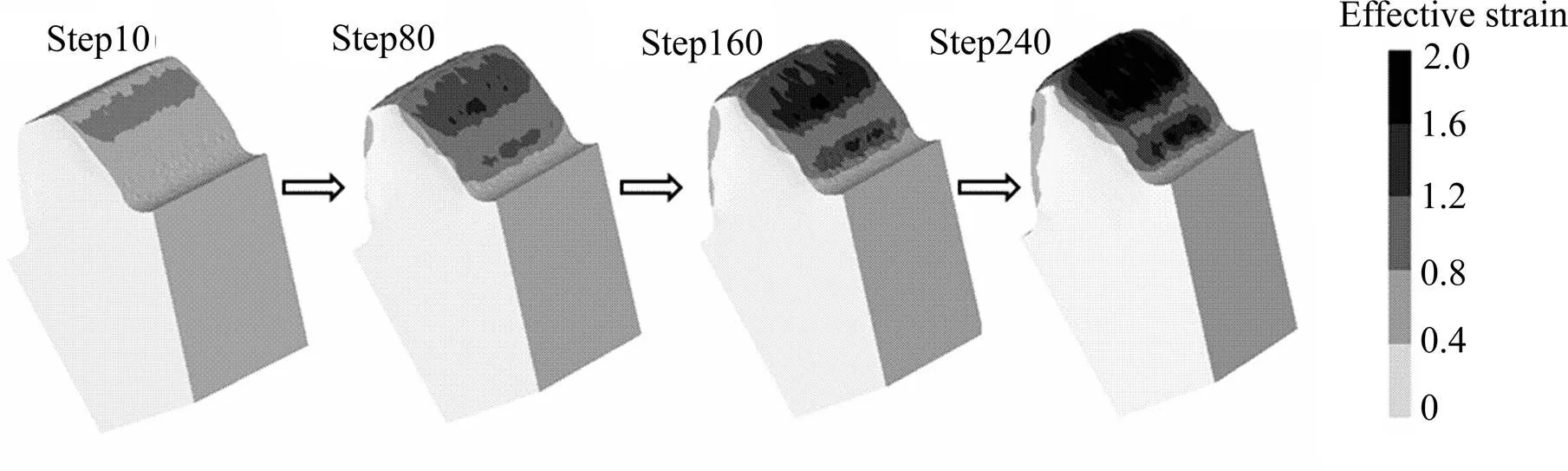
图3 滚压过程中轮齿的等效应变分布云图

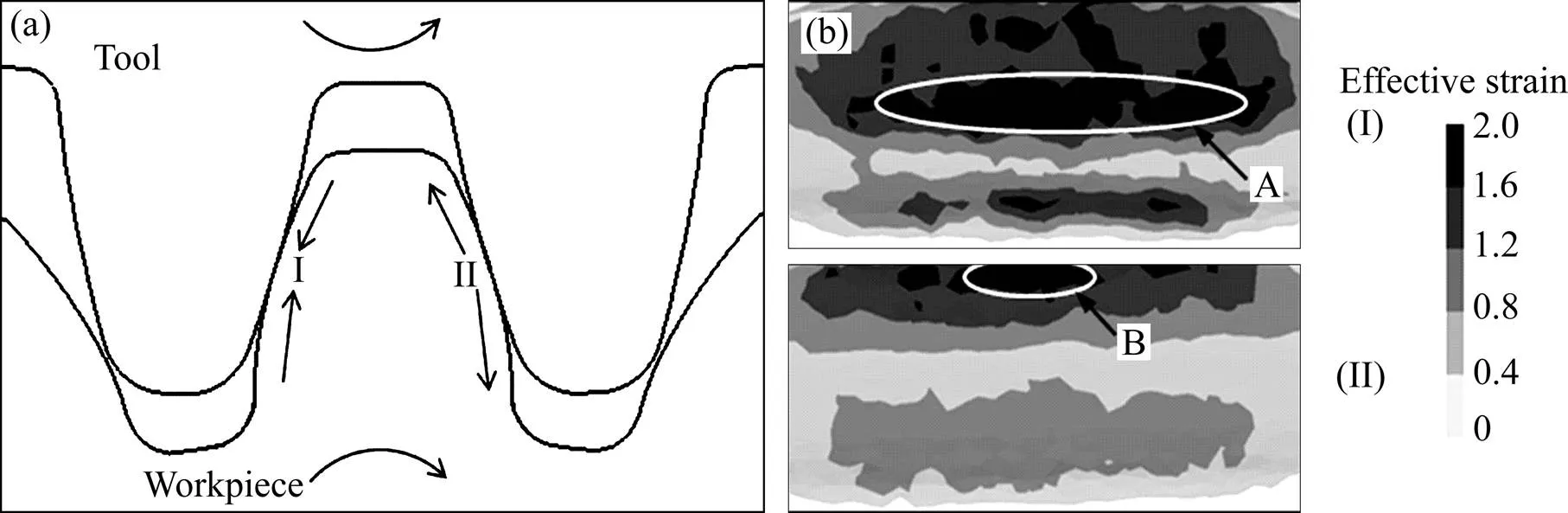
图4 滚压过程中齿轮接触状态示意图(a)与滚压结束后轮齿两侧面的等效应变分布云图(b)

进入滚压面上，等效应变从齿面中心区域向两侧齿端逐渐减小，等效应变较大的区域主要集中在分度圆附近(如图4(b)中A区域)。滚压进行时，由于坯料齿端面不受约束，材料沿齿高方向塑性流动的同时也向两端面移动，即侧向流动，而且轮齿上越靠近两端的区域材料侧向流动越容易，靠近齿端的区域材料沿齿高方向塑性流动小，因而获得的等效应变较小。而且进入滚压面上摩擦力的方向分别由齿顶、齿根指向分度圆[14]，与材料塑性流动方向一致，加剧了材料在齿轮分度圆附近累积，使得该区域内待变形的应变量增大，经过滚压后获得的等效应变也大。

退出滚压面上，同样存在中心区域等效应变大于齿端区域，最大应变出现在齿顶附近(如图4(b)中B区域)。这是由于退出滚压面上的摩擦力方向是由分度圆分别指向齿顶与齿根，齿顶由于材料累积，所以变形大、应变大。由于坯料加工余量的存在，工具轮进给量较小时，坯料齿根并未与工具轮的齿顶接触，齿根几乎不发生变形；当工具轮进给量增大时，坯料齿根与工具轮齿顶易发生刮擦，导致根部表面金属脱落，影响齿根部的变形，所以齿根应变较小。

2.2 应力场

图5为滚压过程中轮齿的等效应力分布云图。由图可见，在滚压的初期(step10到step80)和中期(step80到step160)，应力增长幅度大，滚压后期(step160到step240)应力增长幅度较小。滚压刚进行时(step10)，坯料轮齿中存在较多孔隙，在工具轮的滚压力作用下，材料内部孔隙被压缩，表面产生加工硬化，刚度增加，因此等效应力增加幅度较大。随着孔隙数量减少，材料已接近全致密，轮齿不再发生较大变形，故应力基本不变。滚压结束后(step240)，最大应力位于表层接触面区域，约为900 MPa，心部应力最小，约为 400 MPa，这是因为表层滚压力大，材料发生屈服，滚压力渗到坯料内部而导致这种梯度分布。在有限元计算中，等效应力可反映复杂应力状态下材料的变形抗力。粉末冶金零件变形进入塑性阶段后，随着变形量增加等效应力也增加，反之应力越大的区域致密化效果越好[15]。

2.3 致密度

图6所示为滚压结束后，轮齿上距离齿端面0、1、3和5 mm的4个截面的相对密度分布云图。相对密度从轮齿表层到心部成梯度分布，表面形成约0.3~ 0.5 mm厚度的致密层(相对密度≥0.98)，心部仍然保持初始相对密度。齿轮两侧的致密层厚度存在差异，左侧(进入滚压面)致密层厚度略大于右侧(退出滚压面)。图6显示轮齿端面(见图6(a))的致密效果明显差于其他几个截面，距离端面大于1 mm的截面致密层分布大体一致。这与前文中提到的侧向流动有关，侧向流动导致端面变形不充分，降低了致密化效果，使其致密层厚度小于其他截面。

图7所示为轮齿上相应追踪点(见图1)的相对密度随时间的变化曲线。从图7(a)看出在滚压力的作用下，各个取点区域的相对密度均随时间延长而增大；越靠近轮廓表面，材料密度增幅越大。滚压结束后，P1、P2、P3点的相对密度均大于0.99，距离齿廓表面0.7 mm的P4点，相对密度约为0.96，位于轮齿中心的P5点的密度增长幅度最小，从滚压前的相对密度0.9增大到0.92。对比图7(b)和图3发现，轮齿的密度分布规律和应变分布规律存在较好的一致性，应变大的区域相对密度较高。

图5 滚压过程中轮齿中心面等效应力分布云图

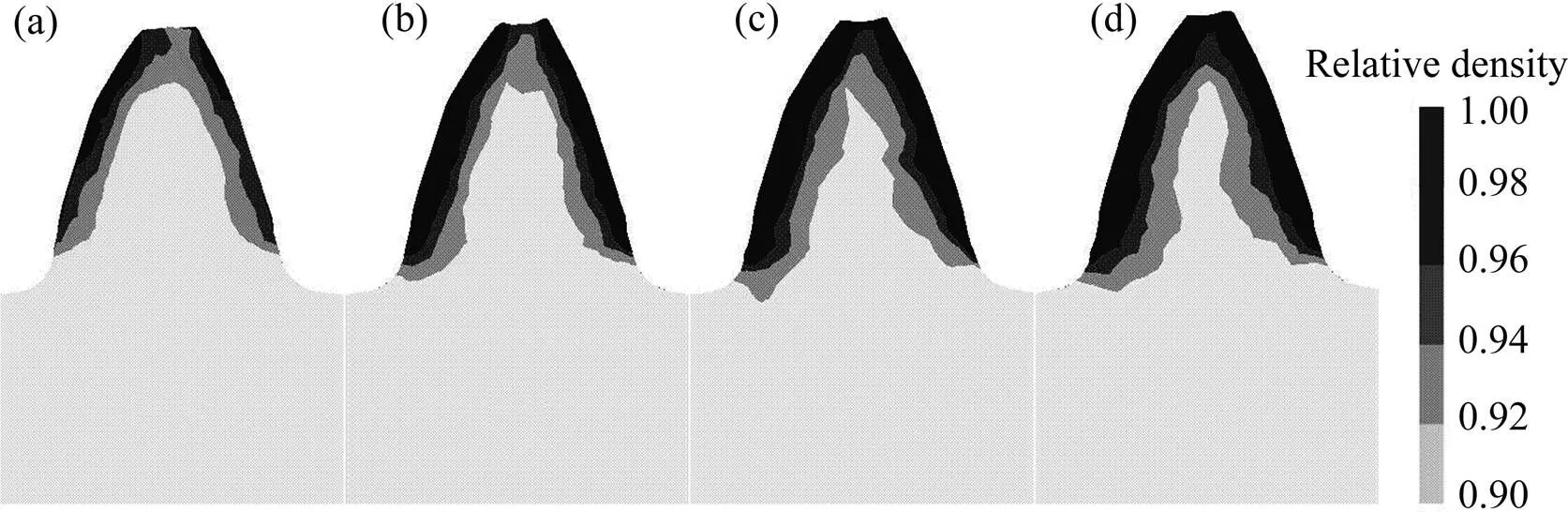
图6 轮齿不同截面上的相对密度分布云图

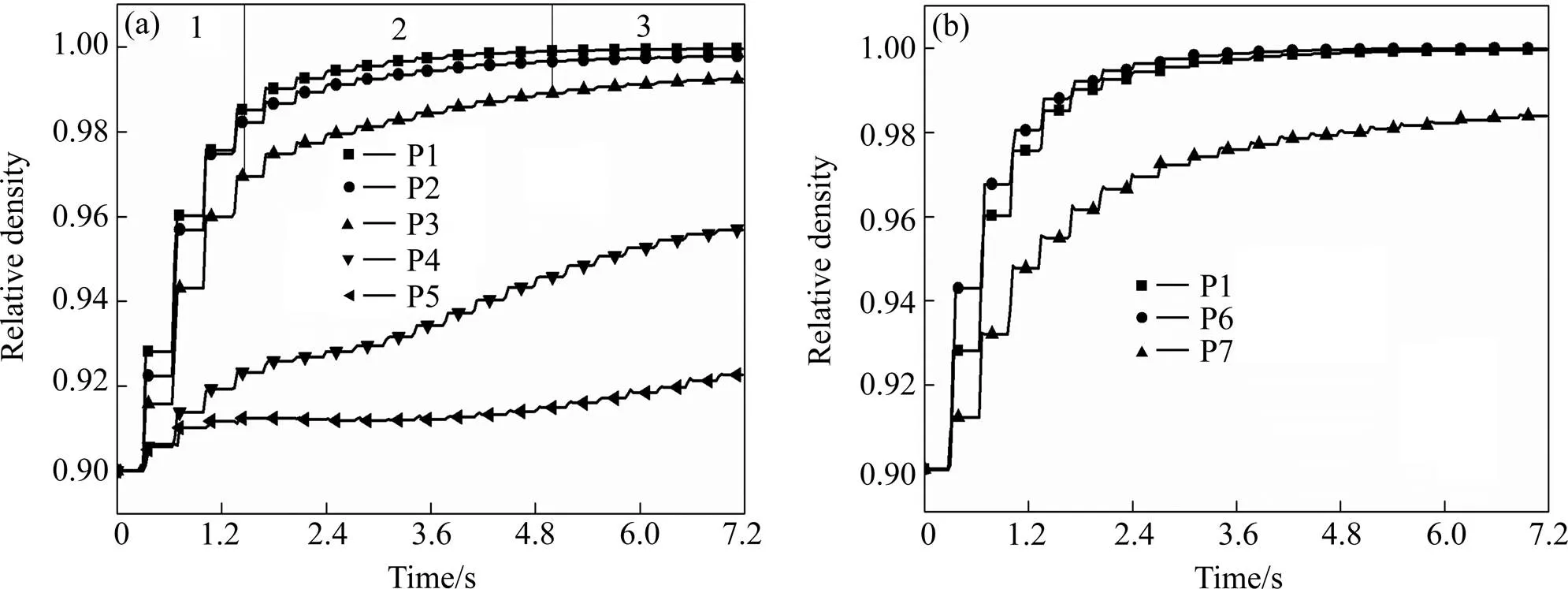
图7 滚压过程中轮齿上追踪点(见图1)的相对密度随时间的变化

致密层区域(见图7(a)中P1、P2和P3点)的相对密度随时间变化曲线显示，齿轮坯料的致密化过程可分为3个阶段。第1阶段为快速压实阶段。由于滚压初期材料内部孔隙较多，在滚压力的作用下，轮齿区域内形成较大的静水压力，使孔隙发生变形与收缩，与工具轮齿面直接接触的坯料轮齿表层孔隙率下降，相对密度大幅度提高。第2阶段为相对密度缓慢增长阶段，随着滚压的进行，材料密度逐渐提高，孔隙尺寸减小，材料产生加工硬化，使得孔隙闭合所需要的静水压力显著增大，因此静水压力对进一步致密化的作用下降。另一方面，滚压力施加到孔隙上的应力状态中还含有剪切应力分量，使孔隙在压扁的同时两侧沿内表面发生剪切变形而趋于闭合。第3阶段为相对密度稳定阶段。这一阶段的孔隙闭合仍然依靠剪切应力，由于材料的密度已经接近理论值，因此相对密度几乎不发生变化。

3 实验验证

滚压实验采用的工具轮和齿轮坯料与有限元模型完全一致，工具轮转速和横向进给速度与表1一致，滚压过程采用油润滑。滚压结束后的被滚齿轮与未滚压齿轮的实物对比如图8所示。由图可见，经过滚压后的齿轮有明显的金属光泽，齿顶变尖，齿顶面形成下凹区域。齿顶形成下凹面的原因是坯料在滚压过程中发生塑性变形，齿面材料沿高度方向流动的速度大于心部材料沿高度方向流动的速度。这也与滚压过程中工具轮的进给量和坯料的塑性性能有关，材料在变形过程中发生加工硬化，难以完全避免这种卷曲现 象[16]。

图8 被滚压齿轮与未滚压齿轮实物对比图

滚压结束后，从齿轮横截面沿齿宽中部取样，观察其孔隙分布特性，如图9所示。由图可见滚压工艺对粉末冶金齿轮表面具有良好的致密效果，轮齿表面形成一定厚度的致密层，左齿面致密层厚度约为 0.50 mm，右齿面约为0.38 mm，这与有限元模拟的结果相吻合。

图9 被滚压轮齿中心面的孔隙分布图

4 结论

1) 采用Deform-3D软件对相对密度为90%的Fe- 2Cu-0.6C粉末冶金齿轮表面滚压过程进行有限元模拟，结果显示等效应力、等效应变的分布特征与齿轮坯料的密度分布状况存在较好的一致性，从轮齿表面到心部三者都逐渐减小。齿顶和齿面等效应变量较大的区域，材料的致密度高，等效应力的不均匀分布导致齿轮各处致密度差异。

2) 在滚压初期轮齿表层的相对密度快速提高，工具轮旋转一周后，与工具轮直接接触的约0.5 mm厚度的表面区域相对密度达到0.98。随着滚压进行，相对密度增长变缓，最后趋于稳定。

3) 滚压工艺对粉末冶金齿轮具有良好的致密效果。滚压结束后轮齿部位从表层到心部相对密度呈梯度分布，表面致密层厚度最高达0.5 mm，心部基本保持初始相对密度。滚压实验获得的轮齿密度分布特性与有限元模拟结果一致。

REFERENCES

[1] BARAN M C, WINTERTON P J, HABERBERGER T E, et al. 先进的烧结−硬化材料在汽车齿轮、凸轮及链轮等中的应用[J]. 粉末冶金工业, 2010, 20(5): 13−18. BARAN M C, WINTERTON P J, HABERBERGER T E, et al. Application of sinter-hardenable materials for advanced automotive applications such as gears, cams, and sprockets [J]. Powder Metallurgy Industry, 2010, 20(5): 13−18.

[2] 于 洋, FORDÉN L. 表面致密化——一种提高烧结齿轮性能的有效方法[J]. 粉末冶金技术, 2005, 23(1): 62−74. YU Yang, Linnea Fordén. Surface densification——an effective way to improve the performance of sintered gears [J]. Powder Metallurgy Technology, 2005, 23(1):62−74.

[3] 韩凤麟. 高负载粉末冶金齿轮选择性表面致密化[J]. 粉末冶金工业, 2013, 23(4): 6−17. HAN Feng-lin. Highly loaded P/M gears produced by selective surface densification [J]. Powder Metallurgy Industry, 2013, 23(4): 6−17.

[4] SIGL L S, 韩凤麟. 表面致密化粉末冶金齿轮的性能[J]. 粉末冶金技术, 2012, 30(3): 229−233. SIGL L S, HAN Feng-lin. Properties of surface densified P/M gears [J]. Powder Metallurgy Technology, 2012, 30(3): 229−233.

[5] SIGL L S, RAU G, DENNERT C. 高使用性能粉末冶金零件的表面致密化[J]. 粉末冶金技术, 2012, 30(2): 144−150. SIGL L S, RAU G, DENNERT C. Selective surface densification for high performance P/M components [J]. Powder Metallurgy Technology, 2012, 30(2): 144−150.

[6] NEUGEBAUER R, KLUG D, HELLFRITZSCH U. Description of the interactions during gear rolling as a basis for a method for the prognosis of the attainable quality parameters [J]. Production Engineering, 2007, 1(3): 253−257.

[7] KLOCKE F, SCHRÖDER T, KAUFFMANN P. Fundamental study of surface densification of PM gears by rolling using FE analysis [J]. Production Engineering, 2007, 1(2): 113−120.

[8] PLANITZER F, HATZENBICHLER T, BUCHMAYR B. FEM-supported development of a radial forging process for surface densification of P/M gears [J]. International Journal of Material Forming, 2009, 2(1): 93−96.

[9] YAZICI B A, KRAFT T, RIEDEL H. Finite element modelling of PM surface densification process [J]. Powder Metallurgy, 2008, 51(3): 211−216.

[10] GRÄSER E, HAJECK M, BEZOLD A, et al. Optimized density profiles for powder metallurgical gears [J]. Production Engineering, 2014, DOI:10.1007/s11740-014-0543-1.

[11] TAKEMASU T, SHINBUTSU T. Form rolling for finishing powder metal gears [J]. Gearsolutions, Media Solutions, Inc, 2004: 33−39.

[12] 周朝辉, 曹海桥, 吉 卫, 等. DEFORM有限元分析系统软件及其应用[J]. 热加工工艺, 2003(4): 51−52. ZHOU Chao-hui, CAO Hai-qiao, JI Wei, et al.Application of deform limited liability analysis system software [J]. Hot Working Technoloyg, 2003(4): 51−52.

[13] 薛克敏, 王晓溪, 李 萍, 等. 纯钼粉末多孔烧结材料ECAP的数值模拟及实验[J]. 中国有色金属学报, 2011, 21(1): 198−204. XUE Ke-min, WANG Xiao-xi, LI Ping, et al.Numerical simulation and experiment of pure molybdenum powder sintered material with porosities during ECAP [J]. The Chinese Journal of Nonferrous Metals, 2011, 21(1): 198−204.

[14] 林云峰. 齿轮传动过程中齿面摩擦力变化规律的理论分析[J]. 科技创新导报, 2009(5): 64−65. LIN Yun-feng. Theoretical analysis of the variation of tooth surface friction during gears driving [J]. Science and Technology Innovation Herald, 2009(5): 64−65.

[15] SHIMA S, OYANE M. Plasticity theory for porous metals [J]. Mechanical Science, 1976, 18(6): 285−291.

[16] 郑伟刚, 陈 大. 齿轮的滚压塑性成形技术的研究现状[J]. 塑性工程学报, 2005, 12(4): 43−46. ZHENG Wei-gang, CHEN Da. The situation of studying on technologies of rolling plasticity forming for gears [J]. Journal of Plasticity Engineering, 2005, 12(4): 43−46.

(编辑 汤金芝)

Finite element simulation and experiment of surface densification of P/M Fe-2Cu-0.6C gears by rolling

LUO Yi, TENG Hao, LI Zhi-you, ZHOU Ke-chao

(State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China)

A Three-dimensional finite element model was used to analyze the surface densification of Fe-2Cu-0.6C P/M gears during a rolling process. The distributions of effective strain, effective stress and relative density of the sample during rolling process were obtained. The rolling experiment was conducted using a standard spur tool gear to verify the accuracy of finite element analysis. The simulation results show differences of the effective strain distributions on two opposite flanks of a tooth. On the approach side, the maximum strain occurs near pitch circle while on the trail side the maximum strain is found at tooth tip. The effective stress increases fast at initial rolling process and tends to steady with the number of rolling cycles increasing. The density increasing process of gear tooth could be divided into three stages: fast increasing, slowly increasing and remaining stability. After rolling progress, there exists density distribution gradient with a densified layer about 0.3~0.5 mm at the tooth surface. The experiment results are in better agree with simulation ones, which verified the accuracy of finite element analysis.

PM gears; surface densification; finite element method; Deform-3D

TF12.5

A

1673-0224(2015)6-837-07

国家高技术研究发展计划(863计划)资助项目(2013AA031102)

2014-12-15；

2015-04-16

李志友，研究员，博士。电话：0731-88836264；E-mail:lizhiyou@csu.edu.cn