随机丢包时延网络控制系统动态输出反馈控制

邱 丽, 姚凤麒, 钟小品, 徐 刚

1) 深圳大学机电与控制工程学院, 深圳 518060; 2) 安徽工业大学电气信息学院, 安徽马鞍山 243000



【电子与信息科学 / Electronic and Information Engineering】

随机丢包时延网络控制系统动态输出反馈控制

邱 丽1, 姚凤麒2, 钟小品1, 徐 刚1

1) 深圳大学机电与控制工程学院, 深圳 518060; 2) 安徽工业大学电气信息学院, 安徽马鞍山 243000

针对传感器与控制器、控制器与执行器之间具有随机丢包和时延的网络控制系统, 研究统一建模及动态输出反馈控制问题. 采用多个马尔可夫链分别描述前向通道和反馈通道的随机丢包与时延过程,将闭环网络控制系统建模成具有多个模态的马尔可夫随机跳变系统. 利用增广矩阵技术和李雅普诺夫方法得到闭环系统随机稳定的充分条件,给出动态输出反馈控制器的设计方法. 通过倒立摆系统验证动态反馈控制的有效性.

网络控制系统；统一建模；动态输出反馈控制；随机丢包和时延；马尔可夫链；增广矩阵技术；李雅普诺夫方法

网络控制系统(networked control systems,NCS)是通过网络进行闭环反馈控制的系统,其主要特征是系统各部件(如传感器、控制器、执行器等)之间信息(如参考输入、被控对象输出、控制器输入等)交换都是由网络来实现的[1]. 与传统的点对点控制系统相比,网络控制系统减少了系统布线, 便于系统诊断和维护,提高了系统的灵活性和柔性. 但是，网络在给控制系统带来众多优势的同时, 其通信缺陷及制约也会使得控制系统的性能下降, 甚至失稳.

通常网络通信缺陷和制约可归纳为5种情况[1]: ① 量化问题; ② 数据包丢失;③ 变采样;④ 时延;⑤ 传输受限. 网络中的这些问题使得闭环控制系统的性能下降甚至失稳. 因此，研究这些问题对系统性能的影响是很重要的.

近年来,针对网络的丢包、时延、量化、时变传输时延等问题的研究已取得很多成果.例如:文献[2-4]研究了网络丢包问题；文献[5-6]研究了网络诱导时延问题；文献[7]研究了量化问题；文献[8-9]和文献[10-11] 分别研究了时变传输间隔及网络资源受限问题；文献[12]同时考虑了量化和网络时延问题；文献[13-16]同时考虑了数据包丢失和网络时延；文献[13]还研究了具有随机丢包时延的不确定非线性NCS的鲁棒H∞滤波问题；文献[15]采用滚动优化原理,研究具有时延及数据包失序的NCS滚动时域H∞控制问题；文献[16]采用Lyapunov稳定性定理及线性矩阵不等式方法研究具有随机丢包和时延的NCS的状态反馈控制问题.文献[17]同时考虑了数据丢包和传输受限；文献[18]同时考虑了时变的采样间隔和网络时延；文献[19]同时考虑了时变的采样间隔和传输受限.另外，文献[20]研究量化、变采样及传输受限等问题；文献[21]考虑丢包、变采样及传输受限等问题. 文献[1]研究时延、变采样及传输受限等问题.

然而,上述几种典型的网络制约往往同时存在于网络中.为了研究网络控制统一建模，本研究基于马尔可夫跳变理论,研究前向通道和反馈通道中同时具有随机丢包和时延的NCS动态输出反馈控制问题, 主要包括:①采用多马尔可夫链统一建模前向通道和反馈通道间的随机丢包和时延;②采用增广矩阵技术处理网络诱导的随机时延,只需构造相对简单的李雅普诺夫函数就能使得闭环系统随机稳定;③采用动态输出反馈控制器镇定闭环控制系统;④数值仿真验证结果的有效性.

1 问题描述

考虑图1所示的网络控制系统.被控对象、传感器、控制器及执行器通过网络分开分布. 网络诱导的随机时延及丢包同时存在于传感器与控制器及控制器与执行器之间. 假设传感器、控制器、执行器是时间驱动; 控制器总是使用最新的数据(如果旧的数据包和新的数据包同时到达,控制器使用新的数据,旧的数据舍弃)[22].

图1 随机丢包与时延的NCS结构图[22]Fig.1 Block diagram of a NCS with packet dropouts and time delays

离散时间线性被控对象模型为

(1)

其中，xp(k)∈n是系统状态；(k) ∈m和y(k)∈p分别表示控制输入和测量输出；A、B和C是具有适当维数的实常矩阵.

采用一个具有以下状态空间实现的动态输出反馈控制器

(2)

其中，xc(k)∈n是控制器的状态；Ac、Bc、Cc和Dc是待定的适当维数实矩阵.

如图1所示,随机有界时延分别存在于传感器与控制器以及控制器与执行器之间.d(k)≥0和τ(k)≥0分别表示传感器与控制器之间及控制器与执行器之间的随机时延.假设d(k)和τ(k)是有界的,取值范围为0≤d(k)≤d及0≤τ(k)≤τ, 其中，d和τ分别表示前向通道和反馈通道随机时延的最大步长.描述时延d(k)和τ(k)的一种方法是用两个相互独立的有限状态的齐次马尔可夫链进行建模[23-24].采用马尔可夫链来描述随机时延的优点是，在实际网络中,当前时刻的时延通常和前一时刻的时延有关[23]. 本研究采用两个独立的齐次马尔可夫链d(k)和τ(k)建模前向通道和反馈通道之间的随机时延,给出相应的状态转移概率λmn和τij.

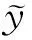
(3)

其中，

(4)

(5)

令

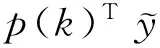
由此得到

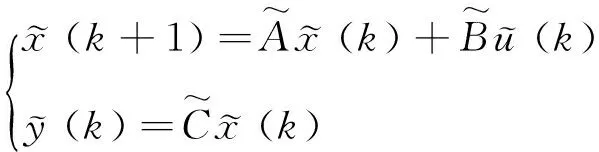
(6)

其中(I表示单位矩阵)，

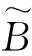
同理，令

则

(7)

其中，

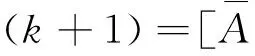
(8)

式中:

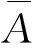
成立,则闭环系统(8)称为随机稳定的.

2 主要结果

首先给出使闭环系统(8)随机稳定的充分条件.

L(i,m,p) =

(9)

【证】 选取如下Lyapunov函数

V(k)=x(k)TPμ(k), d(k), τ(k)x(k)

(10)

记μ(k)=i,d(k)=m,τ(k)=p, 沿着闭环系统(8)求解得

E[ΔV(k)]=E[V(k+1)]-V(k)=

E[x(k+1)TPμ(k+1), d(k+1), τ(k+1)x(k+1)]-

x(k)TPμ(k), d(k), τ(k)x(k)=

Pi, m, p)x(k)=x(k)TL(i,m,p)x(k)

(11)

结合式(9),由式(11)可得

E[ΔV]≤ -λmin(-L(i,m,p))x(k)Tx(k)≤

-βx(k)Tx(k)

(12)

E[V(k+1)]-E[V(0)]≤

(13)

可得,

令T→ ∞,得

(14)

因此，由式(14)和定义1可知闭环系统(8)是随机稳定的.

证毕.

本研究采用增广矩阵技术处理网络带来的随机时延d(k)和τ(k), 将具有随机丢包时延的NCS建模为不包含时滞项的闭环系统(8). 增广矩阵技术避免了构造复杂的Lyapunov函数,只需构造相对简单的Lyapunov函数,就能得到闭环系统(8)随机稳定的充分条件,避免了复杂的公式推导和运算.

定理1给出了在动态输出反馈控制率K作用下,闭环系统(8)随机稳定的一个充分条件. 基于该条件,可以导出系统(1)的动态输出反馈控制器设计方法.

由Schur补引理可知，式(9)等价于以下的矩阵不等式

(15)

其中,

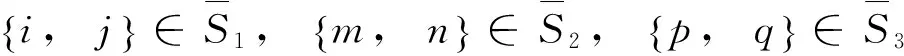
为了有效处理非线性矩阵不等式(15), 记不等式(15)左边的矩阵为Ωi,m,p, 用Xj,n,q代替Ωi,m,p中的P-1j,n,q, 得到式(17). 其中,Xj,n,q为正定矩阵. 采用锥补线性化(conecomplementaritylinearization,CCL)算法可将动态输出反馈控制器的求解问题转化为定理2中求解具有线性矩阵不等式约束的最小化问题.

(16)

(17)

(18)

其中,

步骤1:采用feasp求解器寻找满足式(17)和(18)的一组可行解(P0i,m,p,X0i,m,p,K0), 令k=0.

步骤2:采用mincx求解器求解以下有关(Pi,m,p,Xi,m,p,K)的LMI优化问题

得

Pi,m,p,Xi,m,p,K, 令Pk+1i,m,p=Pi,m,p,Xk+1i,m,p=Xi,m,p,Kk+1=K.

步骤3: 如果Pi,m,p满足式(15), 则退出, 得到的解即为此最小化问题的一个解; 否则, 令k=k+1, 然后返回到步骤2.

3 数值仿真

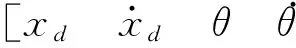
图2 倒立摆控制系统[24] Fig.2 Inverted pendulum system

设采样周期为Ts=0.1s, 给如下的线性离散时间模型设计输出反馈控制器,被控对象相应参数为

系统矩阵A的4个特征根分别为1.000、1.000、1.556 9和0.462 3,因此该离散系统是开环不稳定系统.

设在初始输出y=[-0.1 0.1]T下，由定理2得动态输出反馈控制器的增益矩阵为

Cc=[-3.251 3 1.902 2 -9.623 5 8.045 4],

Dc=[3.852 1 40.603 5].

3个马尔可夫链的值及系统输出轨迹线分别如图3至图6所示.

图3 跳变参数 μ(k)Fig.3 Jumping parameter μ(k)

图4 传感器与控制器间随机时延d(k)Fig.4 S-C Random delays d(k)

图5 控制器与执行器间随机时延τ(k)Fig.5 C-A random delays τ(k)

图6 系统输出响应Fig.6 State response

从图6可知, 系统在动态输出反馈控制器作用下是稳定的.

图6中两条状态相应曲线分别表示小车的位置xd和倒立摆的角位置θ, 数值仿真结果表明系统是随机稳定的. 仿真结果验证了本研究提出的控制方法的有效性.

结 语

采用马尔可夫跳变系统方法,研究了一类带有网络诱导丢包和时延的NCS动态输出反馈控制问题, 建立了新的闭环控制系统模型.采用增广矩阵方法避免了构造复杂李雅普诺夫函数, 设计了具有闭环系统随机稳定的动态输出反馈镇定控制器.

/ References：

[1] Donkers M C F, Heemels W P M H, Wouw van de N, et al. Stability analysis of networked control systems using a switched linear systems approach [J]. IEEE Transactions on Automatic Control, 2011,56(9): 2101-2115.

[2] Sun Yeguo, Qin Shiyin. Stability and stabilization of networked control systems with bounded packet dropout [J]. Acta Automatica Sinica, 2011, 37(1): 113-117.

[3] Jia Tinggang, Niu Yugang,Wang Xingyu. H1 control for networked systems with data packet dropout [J]. International Journal of Control Automation, and Systems, 2010, 8(2): 198-203.

[4] Lu Qiugang, Zhang Lixian, Basin M, et al. Analysis and synthesis for networked control systems with uncertain rate of packet losses [J]. Journal of the Franklin Institute, 2012, 349(7): 2500-2514.

[5] Qiu Li, Xu Bugong, Li Shanbin. H2/H∞control of networked control systems with random time delays [J]. Science China: Information Sciences, 2011, 54(12): 2615-2630.

[6] Zhang Wenan, Yu Li. A robust control approach to stabilization of networked control systems with short time-varying delays [J]. Acta Automatica Sinica, 2010, 36(1): 87-91.

[7] Ishido Y, Takaba K, Quevedo D E. Stability analysis of networked control systems subject to packet-dropouts and finite-level quantization [J]. Systems and Control Letters, 2011, 60(5): 325-332.

[8] Iza M, G orges D, Liu S. Optimal control of networked control systems with uncertain time-varying transmission delay [C]// 2nd IFAC Workshop on Distributed Estimation and Control in Networked Systems. Annecy(France): IFAC, 2010: 13-18.

[9] Fujioka H. A discrete-time approach to stability analysis of systems with aperiodic sample-and-hold devices [J]. IEEE Transactions on Automatic Control, 2009, 54(10): 2440-2445.

[10] Suzuki T, Kono M, Takhashi N, et al. Controllability and stabilizability of a networked control system with periodic communication constraints [J]. System and Control Letter, 2011, 60(12): 977-984.

[11] Wu Xiaofeng, Giu Weihua, He Jianjun. Stability analysis of networked control system with control channels constraints and time delay [J]. International Journal of Digital Content Technology and its Applications, 2012, 6(7): 151-158.

[12] Liberzon D. Quantization, time delays, and nonlinear stabilization [J]. IEEE Transactions on Automatic Control, 2006, 51(7): 1190-1195.

[13] Dong Hongli, Wang Zidong, Gao Huijun. Robust H1 filtering for a class of nonlinear networked systems with multiple stochastic communication delays and packet dropouts [J]. IEEE Transactions on Signal Processing, 2010, 58(4): 1957-1966.

[14] Wang Yulong, Yang Guanghong. Time delay and packet dropout compensation for networked control systems: A linear estimation method [J]. International Journal of Control, 2010, 83(1): 115-124.

[15] Liu Andong, Yu Li, Zhang Wenan. One-step receding horizon H1 control for networked control systems with random delay and packet disordering [J]. ISA Transactions, 2011, 50(1): 44-52.

[16] Qiu Li, Luo Qin, Gong Feng, et al. Stability and stabilization of networked control systems with random time delays and packet dropouts [J]. Journal of the Franklin Institute, 2013, 350(7): 1886-1907.

[17] Wang Yongqiang, Ye Hao, Ding S, et al. Fault detection of networked control systems subject to access constraints and random packet dropout[J]. Acta Automatica Sinica, 2009, 35(9): 1230..1234.

[18] Van D W N, Naghshtabrizi P, Cloosterman M, et al. Tracking control for sampled-data systems with uncertain sampling intervals and delays [J]. International Journal Robust Nonlinear Control, 2010, 20(4): 387-411.

[19] Walsh G, Elidman O, Bushnell L. Asymptotic behavior of nonlinear networked control systems [J]. IEEE Transactions Automatic Control, 2001, 46(7): 1093-1097.

[20] Carnevale D, Teel A, Nesic D. A Lyapunov proof of improved maximum allowable transfer interval for networked control systems [J]. IEEE Transactions Automatic Control, 2007, 52(5): 892-897.

[21] Neeic D, Liberzon D. A unified approach to controller design for systems with quantization and time scheduling [C]// Proceeing of the 46th IEEE Conference on Decision and Control. New Orleans(USA): IEEE Press, 2007, 3939-3944.

[22] Tian Engang, Yue Dong. A new state feedback H1 control of networked control systems with time-varying network conditions [J]. Journal of the Franklin Institute, 2012, 349(3): 891-914.

[23] Nilsson J. Real-time control systems with delays [D]. Lund, Sweden: Lund Institute of Technology, 1998.

[24] Zhang Liqian, Shi Yang, Chen Tongwen, et al. A new method for stabilization of networked control systems with random delays [J]. IEEE Transactions on Automatic Control, 2005, 50(8): 1177-1181.

【中文责编：方 圆；英文责编：木 南】

Dynamic output feedback control of networked control systems with random packet dropouts and time delays

Qiu Li1, Yao Fengqi2, Zhong Xiaopin1, and Xu Gang1†

1) College of Mechatronics and Control Engineering, Shenzhen University, Shenzhen 518060, P.R.China 2) School of Electrical Engineering and Information, Anhui University of Technology,Maanshan 243000, Anhui Province, P.R.China

Unified modeling and dynamic output feedback control are considered for a class of networked control systems (NCSs) with random sensor-to-controller (S-C) and controller-to-actuator (C-A) packet dropouts and time delays. The packet dropouts and time delays in forward channels and feedback channels are modeled as multiple Markov chains and the closed-loop NCS is modeled as a Markovian jump linear system with multiple Markov chains. Based on the augmenting matrix technique and Lyapunov method, a sufficient condition is derived for the stochastic stability of the closed-loop NCS, and a design procedure is presented for the dynamic output feedback controller. The inverted pendulum system illustrates the effectiveness of the proposed method.

networked control systems; unified modeling; dynamic output feedback control; random packet dropout and time delay; Markov chains; augmenting matrix technique; Lyapunov method

：Qiu Li, Yao Fengqi, Zhong Xiaopin, et al. Dynamic output feedback control of networked control systems with random packet dropouts and time delays[J]. Journal of Shenzhen University Science and Engineering, 2015, 32(1): 40-47.(in Chinese)

TP 273

A

10.3724/SP.J.1249.2015.01040

国家自然科学基金资助项目(61403258); 广东省自然科学基金资助项目(S2013040016183);深圳市科技计划知识创新计划基础研究项目(JCYJ20140418182819 153)

邱 丽(1981—), 女(汉族)，河南省信阳市人，深圳大学讲师、博士.E-mail:qiuli@szu.edu.cn

Received：2014-03-17；Accepted：2014-10-24

Foundation：National Natural Science Foundation of China(61403258); Natural Science Foundation of Guangdong Province(S2013040016183); Shenzhen Science and Technology Research Foundation for Basic Project(JCYJ20140418182819153)

† Corresponding author：Professor Xu Gang. E-mail: xugang@szu.edu.cn

引 文：邱 丽, 姚凤麒, 钟小品，等.随机丢包时延网络控制系统动态输出反馈控制[J]. 深圳大学学报理工版，2015，32(1)：40-47.