基于果蝇优化的SVM回归模型及其应用研究

吴 悦

(淮阴工学院 现代教育技术中心，江苏 淮安 223003)

基于果蝇优化的SVM回归模型及其应用研究

吴 悦

(淮阴工学院 现代教育技术中心，江苏 淮安 223003)

为了有效解决支持向量机模型在参数选择上的盲目性，提高该模型的学习性能和泛化能力，提出一种基于果蝇优化的SVM方法。该方法首先运用果蝇优化算法选择全局最优的SVM惩罚因子和核函数参数，建立SVM分类模型，进而将该模型应用于对有机化合物的熔点预测问题中。实验结果表明，基于果蝇优化的SVM模型效率高，实际应用效果好。

支持向量机；果蝇；有机化合物；熔点；预测

0 引言

近年来，物质的基础物性已有大量的实测数据，但是与生产和科研所涉及的物质种类相比，仍然很不充分，所以常常需要对有关物质的未测物性进行预测。以此为需求，以人工神经网络为代表的人工智能技术开始在化工领域逐渐得到广泛的应用，但该模型常具有需要样本数据多、收敛速度慢、易陷入局部最小的缺点。而支持向量机[1]具有良好的非线性映射能力，且可以克服神经网络“维数灾难”的固有问题，在小样本条件下具有良好的应用效果。

在支持向量机的应用中，其惩罚因子与核函数参数的选取可以影响其应用效果，且已经成为人们研究的热点问题。其中不乏一些智能优化算法，例如遗传算法[2-3]、粒子群算法[4]等。针对这些算法的问题，研究人员进行了相应的改进和应用，例如量子粒子群优化算法[5]、混沌粒子群优化算法[6-7]。

果蝇优化算法(Fruit fly Optimization Algorithm，FOA)是一种基于随机搜索的全局优化算法，该算法通过模拟果蝇觅食行为实现对最优位置的搜索[8-9]。本文将FOA与支持向量机参数优化问题相结合，提出一种基于FOA的SVM回归模型( FOA-SVM)，该方法利用FOA算法搜索最优的支持向量机回归模型参数，建立最优的SVM回归模型，将该算法应用到有机化合物熔点的预测中，从有机化合物的分子量、临界密度、正常沸点和偶极矩预测其熔点，预测结果表明其具有较好的实际效果。

1 基于FOA的SVM参数优化

果蝇优化算法于2011年提出，该算法的基本流程如下：

(1) 参数初始化。初始化果蝇群体规模、果蝇搜索代数、果蝇群体位置坐标(x，y)。

(2) 果蝇个体初始化。在果蝇群体周围，利用果蝇嗅觉搜索食物，从而对果蝇个体进行初始化。

(1)

式中，Lr为步长大小，取值范围为[-L，L]，L为果蝇个体嗅觉搜索的固定步长值。

(3) 味道浓度判断值计算。采用式(2)的形式估计第i个果蝇个体与坐标原点的距离di，以式(3)计算味道浓度判定值Si。

(2)

Si=1/di

(3)

(4) 味道浓度值计算。将味道浓度判定值代入到味道浓度判定函数(fitnessfunction)中，从而计算得出该果蝇个体的味道浓度值。

smelli=fitnessfunction(Si)

(4)

(5) 味道浓度比较。找出果蝇群体中味道浓度最优的个体，即

[bestsmellbestindex]=max(smell)

(5)

(6) 味道浓度值比较。判断味道浓度值是否优于前一代，若是，则执行(7)；否则，执行(8)。

(7) 更新果蝇群体位置坐标，保留最佳味道浓度值与最佳果蝇个体的位置坐标，将最佳果蝇个体位置坐标作为新的果蝇群体位置坐标。

smellbest=bestsmell

(6)

(7)

(8) 判断是否找到最优食物位置或迭代结束，若是，则算法结束，否则，执行(2)-(6)。

在支持向量机的基本原理中[10-11]，影响支持向量机性能的参数主要是惩罚因子c和核函数参数g，惩罚因子c控制间隔的最大化和分类误差之间的折衷；核函数参数g影响样本数据在高维特征空间中分布的复杂程度。本文将FOA算法应用于SVM的参数优化中，即将实际问题的适应度函数作为果蝇浓度函数，依据适应度最优的原则采用FOA算法进行迭代寻优，直至算法结束，从而选择最优的模型参数。

2 实例分析

2.1 样本选择

为了验证本文所提出模型的应用效果，本文将该方法应用到有机化合物熔点的预测中。相关研究表明，有机化合物的分子量、临界密度、正常沸点可以作为指标特征预测有机化合物的熔点[12]。样本数据来自文献[12]。预测特征向量选择对熔点预测较好的三个有机化合物属性，包括分子量、临界密度(kg/L)、正常沸点(×10-30℃)。选取150组样本作为数据集，随机选取其中的130组数据作为训练样本，20组数据作为测试样本。典型的基本训练数据如表1所示。

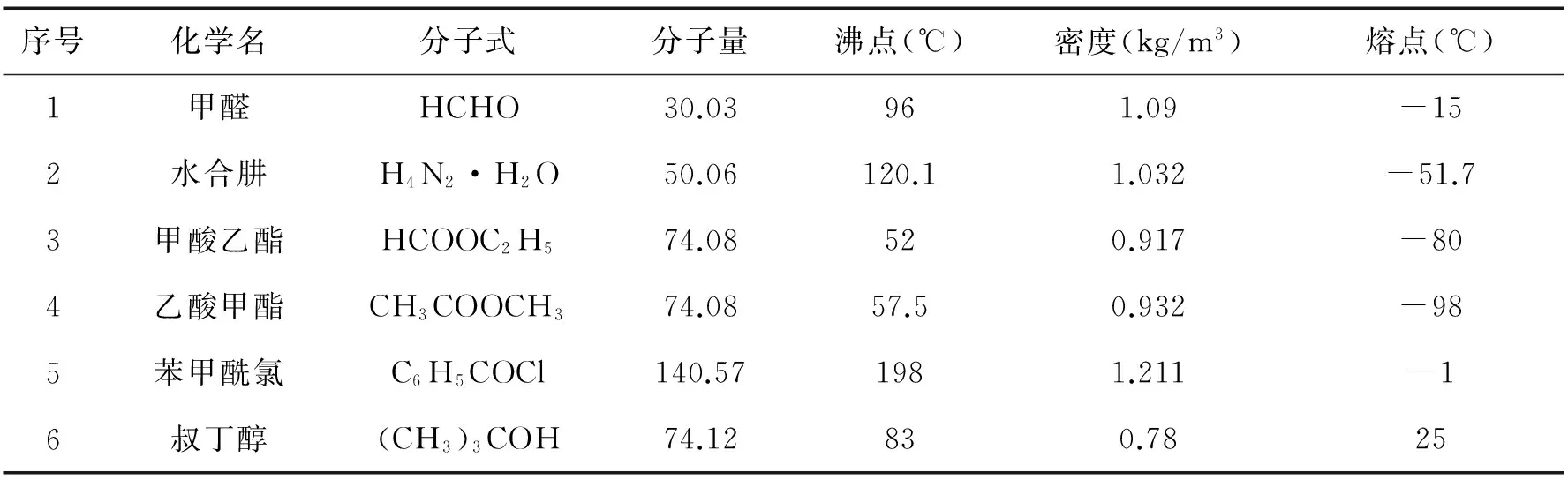
表1 SVM典型训练数据

由于原始样本数据的取值范围大，离散性强，为了便于计算并有效减小误差，需要对原始数据进行归一化处理。本文采用式(8)对输入样本进行归一化处理，

(8)

其中，Xmax和Xmin分别为辅助变量X的上下限值。

2.2 基于FOA的SVM参数优化

以训练样本数据为分析对象，运用果蝇优化算法对SVM回归模型参数c和g进行优化，在觅食空间内搜索具有最优食物浓度值的果蝇个体，从而建立效果最好的SVM回归模型。SVM的参数训练采用3-CV方法，果蝇个体适应度为训练的最低均方误差，果蝇群体个数为10，迭代次数为50。

图1为FOA算法对SVM进行参数优化的曲线图，可以看出，当迭代到第48代时，果蝇群体中出现最优的适应度取值，此时最低均方误差为7.32%，此时所取得的c和g参数认为是SVM回归模型的最优参数。通过计算，此时c=0.85，g=20.04，计算时间为6.18s。可见，FOA算法可以有效地搜索支持向量机回归模型的参数。

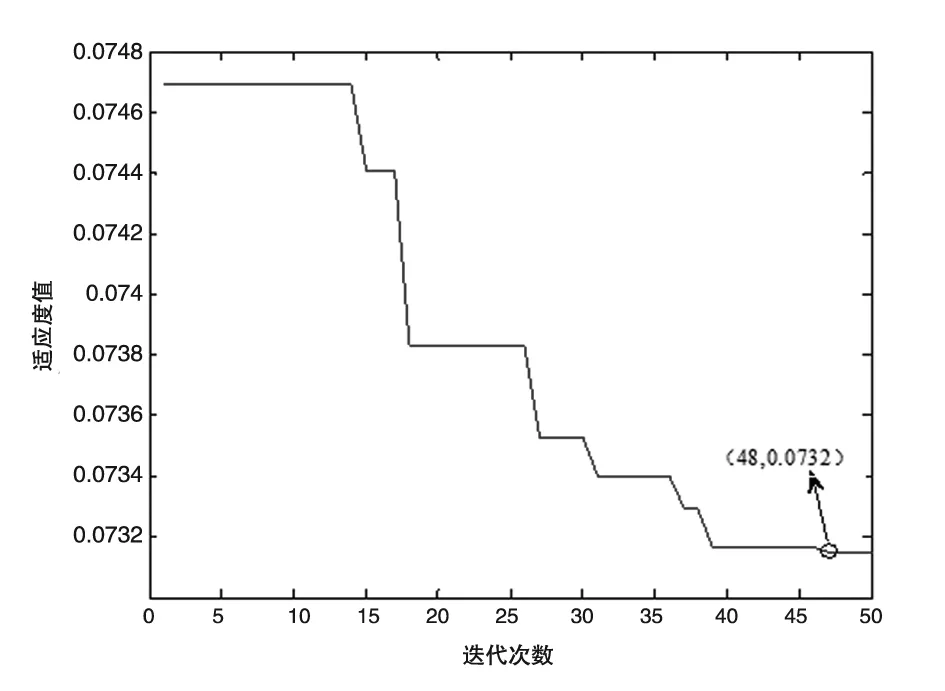
图1FOA进化曲线图

图2显示了搜索过程中果蝇个体的搜索位置分布图，其中，图2(a)为代表参数c的果蝇群体觅食轨迹，图2(b)为代表参数g的果蝇个体。可以看出，代表参数c的历代果蝇在[-15:25；+15:25]的直角坐标系范围内分布，搜索范围广，最优果蝇个体集中。同理，代表参数g的历代果蝇在[-25:20；+25:20]直角坐标系范围内具有一定的搜索能力。

2.3 SVM回归效果与分析

利用FOA优化SVM取得最优参数和训练样本建立SVM回归模型。对20组验证样本进行回归分析，模型的预测结果如图3所示，横坐标为所选取的20个有机物样本取值，纵坐标为归一化的有机物样本熔点。可以看出，预测样本的样本预测值，此时均方误差MSE为3.02%，相关系数为89.39%，此时有机化合物熔点预测取得了较好的效果。

(a)参数c果蝇个体搜索位置

(b)参数g果蝇个体搜索位置

图2 果蝇个体搜索位置图

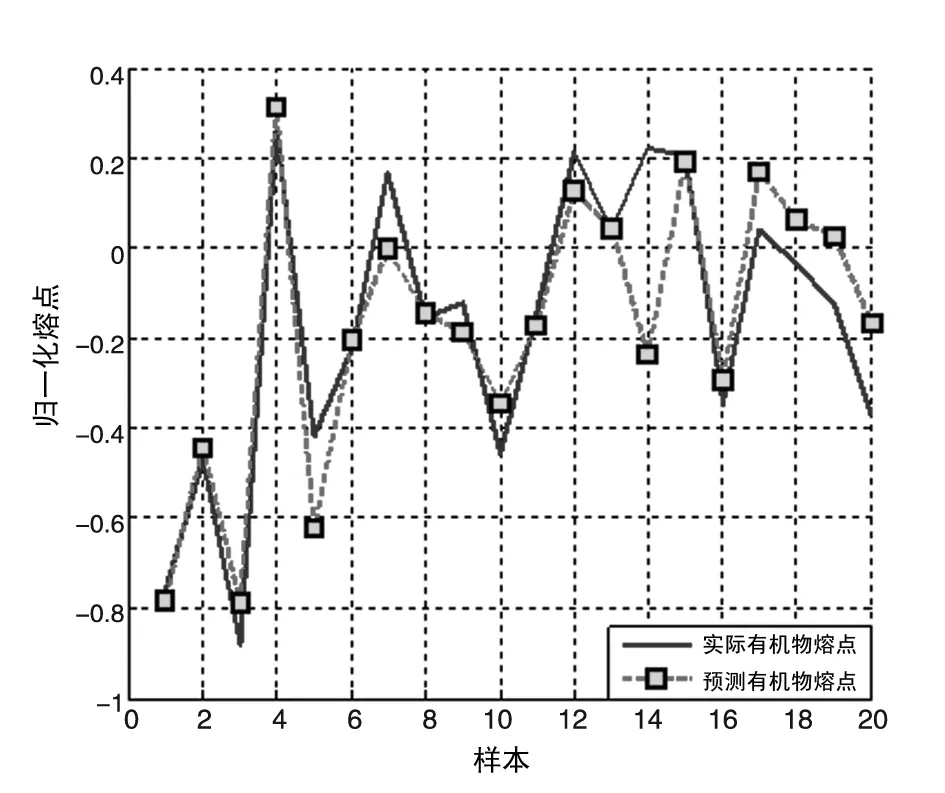
图3 预测结果

3 结论

本文提出了一种基于果蝇优化的SVM方法。该方法首先运用果蝇优化算法选择全局最优的SVM惩罚因子和核函数参数，从而建立SVM分类模型，进而基于该模型对实际问题进行应用。将该模型应用于对有机化合物的熔点预测问题中，实验结果表明，基于果蝇优化的SVM模型效率高，实际应用效果好。

[1] 孙翠娟．基于K型核函数的支持向量机[J].淮海工学院学报:自然科学版，2006，15(4):4-7．

[2] 戴冬雪．基于混沌思想的粒子群优化算法及其应用[J].华中科技大学学报，2005，33(10):53-55．

[3] 孙亚．基于粒子群BP神经网络人脸识别算法[J].计算机仿真，2008，25(8):201-204．

[4] 邓乃扬，田英杰．数据挖掘中的新方法—支持向量机[M].北京:科学出版社，2004．

[5] 王加阳，谢颖.基于量子粒子群优化的最小属性约简算法[J].计算机工程, 2009,35(12):148-153.

[6]AlatasB,AkinE,OaerB.ChaosEmbeddedParticleSwarmOptimizationAlgorithms[J].Chaos,SolitonsandFractals,2007,40 (4):1715-1734.

[7] 唐巍.基于幂函数载波的混沌优化方法及其应用[J] .控制与决策,2005,20(9):1043-1046.

[8]PANWT．Anewfruitflyoptimizationalgorithm:Takingthefinancialdistressmodelasanexample[J]．Knowledge-BasedSystems，2012，26: 69-74．

[9] 潘文超．果蝇最佳化演算法[M].台北：沧海书局，2011．

[10]BURGESJCC.支持向量机用于模式识别[J].DataMiningandKnowledgeDiscovery,1998,2(2):121-167．

[11]VAPNIKV.统计学习理论[M].NewYork:JohnWiley&Sons,1998．

[12] 卢焕章.石油化工基础数据手册[M].北京：化学工业出版社,1982.

(责任编辑:尹晓琦)

“工程结构检测与加固”栏目

孙文彬教授按语：工程结构一般具有生产周期长、影响因素多、经济投入高和使用寿命长等特点，建成后一般不可逆转。工程结构在建造和使用期内，对其可靠性进行科学客观的检测与鉴定，必要时采取有效的加固和补强，提高其功能，延长其寿命。顾爱军的文章研究了声发射技术对钢筋混凝土结构损伤的检测和识别，实验证明该方法可有效预警混凝土结构损伤的两个标志的界限，声发射技术拓展了钢筋混凝土结构无损检测和健康监测理论基础和实践应用。陆路博士的文章研究了激光多普勒测速仪远程微动测量方法、特点，创新解决了建筑结构微振动和固有频率测试方法。顾文虎等在文章中分析了建筑平移工程中托换节点受力特性，介绍了工程应用设计方案及施工技术要点。

SVM Regression Model Based on Fruit Fly Optimization and Its Application

WU Yue

(Modern Educational Technology Center, Huaiyin Institute of Technology,Huai'an Jiangsu 223003, China)

In order to effectively solve the problem of blindness of support vector machine (SVM) model on the parameter selection, improve the learning performance and generalization ability of the model, a SVM based on fruit fly optimization method was put forward. Drosophila optimization was first used as an optimization algorithm to select the global optimal SVM penalty factor and the kernel function parameter so as to establish the SVM classification model, which was then used to simulate the actual problem. The model was applied to predict melting point of organic compounds. The experimental results showed that the SVM based on fruit fly optimization model had high efficiency and good effect in practical application.

support vector machine (SVM); fruit fly; organic compounds; melting point; prediction

2014-12-17

吴悦(1976-)，女，湖北汉川人，工程师，硕士，主要从事网络安全、数据挖掘研究。

TP391

A

1009-7961(2015)01-0018-03