PM2.5 测量系统中改进神经网络控制算法优化补偿
2015-03-06邹孔雨佟国香
邹孔雨,佟国香
(上海理工大学 光电信息与计算机工程学院,上海 200093)
随着大气中PM2.5 的监测浓度上升趋势增大,其对身体健康,大气能见度以及大气环境污染具有显著地危害和潜在的影响,被称为“灰霾元凶”,PM2.5 是指空气动力学直径≤2.5 μm 的大气颗粒物。PM2.5对大气环境有着严重的影响,由于细颗粒物质的散光作用及其对光较强的吸收作用,导致大气能见度降低,从而给交通运输和日常生活带来不便,严重时甚至可导致事故。
PM2.5 对人体健康影响严重,其浓度的增高与心肺疾病的发病率,死亡率息息相关。
由于PM2.5 测量系统在测量过程中,会受到各种环境因素的影响,使用时间一长,会使测量精度下降,在实际设计中要提高整个系统的测量精度,通常选择测量精度高的灰尘传感器,但成本较高。故为了控制成本,需选择经济型的灰尘传感器,并在实际测量中对影响其测试精度的因素进行补偿。文献[1]中提出了一种基于递归神经网络的加速度传感器动态性能补偿方法,文献[2]中给出了一种基于改进遗传RBF 神经网络的传感器动态特性补偿算法,文献[3]中给出了一种物联网框架下PM2.5 高精度测试模型仿真分析,文献[4]中给出了一种基于β 射线吸收法的PM2.5 测量技术的研究。
综合分析,本文提出了一种改进的BP 神经网络PID 算法对PM2.5 测量系统进行优化补偿,并通过仿真验证了其有效性。
1 系统优化补偿原理
用灰尘传感器设计的PM2.5 测量系统,用于室内灰尘,烟雾的测量,在无污染的环境下,系统本身会有一个初始电压,称为无尘电压v,环境灰尘浓度为x,输出电压为y,假设输出电压与灰尘浓度以及无尘电压的关系为

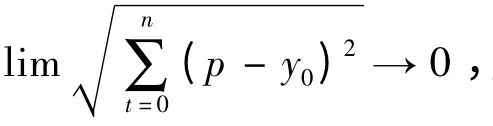
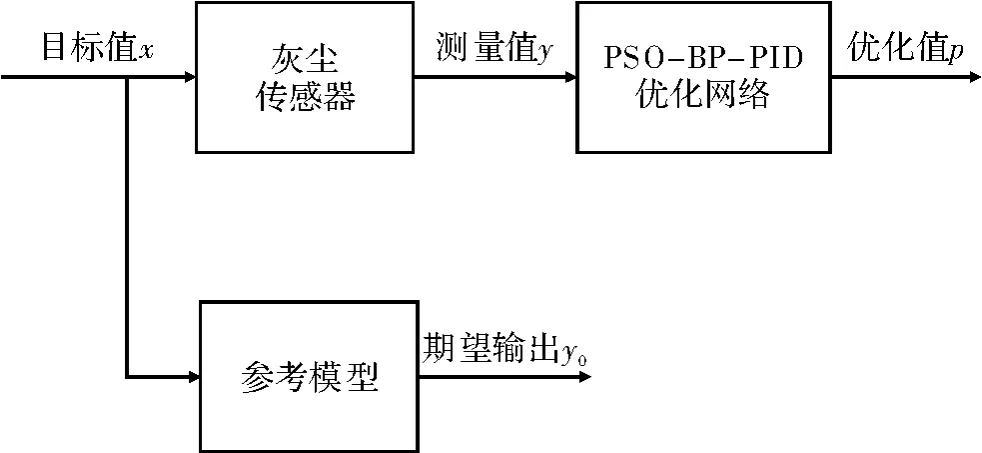
图1 优化网络框图
2 PSO-BP-PID 优化算法
2.1 PID 控制
经典PID 控制已极为成熟,其算法简单,可靠性高及鲁棒性好,已被广泛应用于各种工业领域[5]。在PID 控制中,经典增量式数字PID 控制算式为式(2)
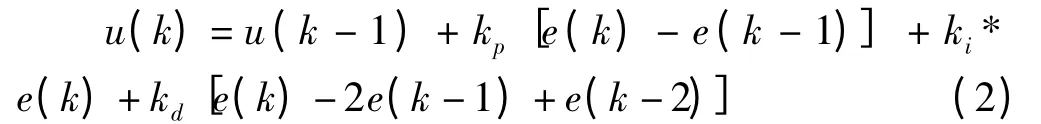
式中,kp,ki,kd分别为比例系数、积分系数和微分系数;u(k)是控制器的输出。
目前测量中常用的PID 控制,其控制参数是固定不变的,而测量系统所处的环境具有大量不确定性因素,传统上的PID 控制已难以满足测量需求。神经网络的自学习能力以及非线性模型逼近的能力,可较好地改善参数的在线整定问题。为了提高测量的准确性,避免传统PID 的不足,引入BP 神经网络是一种有效的解决方法。由于BP 神经网络算法容易陷入局部最优,收敛速度慢,针对这个缺点,文中先用PSO 优化算法对BP 神经网络进行优化。
2.2 改进的粒子群优化算法的BP 神经网络
粒子群优化算法(Particle Swarm Optimization,PSO),是一种基于群体智能的全局随机搜索算法,其通过追随当前搜索到的最优值来寻找全局最优。粒子群优化算法要先对粒子进行初始化,接着经过数次的迭代寻找最优解。粒子的速度和位置分别按照下式进行更新
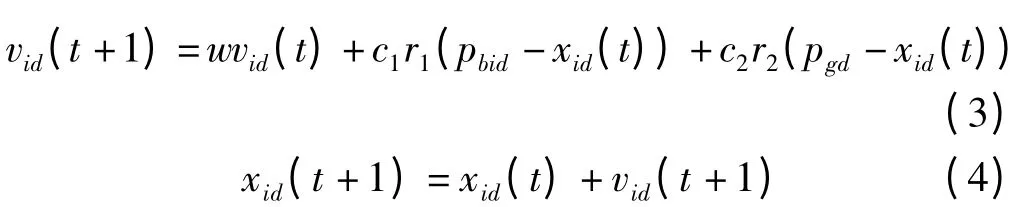
式中,vid是粒子速度;xid是粒子位置;w 是权重因子,用于调节对解空间的搜索范围;c1和c2是学习因子,调节学习步长,一般c1=c2=2,r1,r2是[0,1]内的随机数,pbid为个体极值,pgd为全局极值。
由速度式(3)可知,粒子速度由权重,学习因子和随机数共同决定,可通过减少参数,避免通过经验对学习因子进行调整
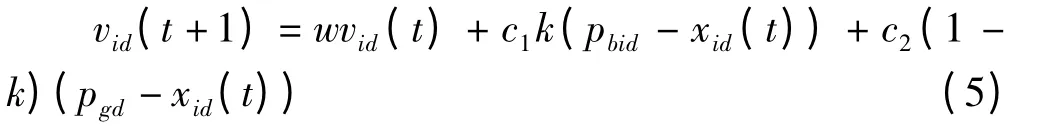
式(5)中,通过线性递减粒子群的局部最优和递增全局最优的影响控制例子速度,增强了粒子群的全局搜索能力。
BP 神经网络[6]采用3 层结构,其由输入层,隐含层和输出层组成,其结构如图2 所示。
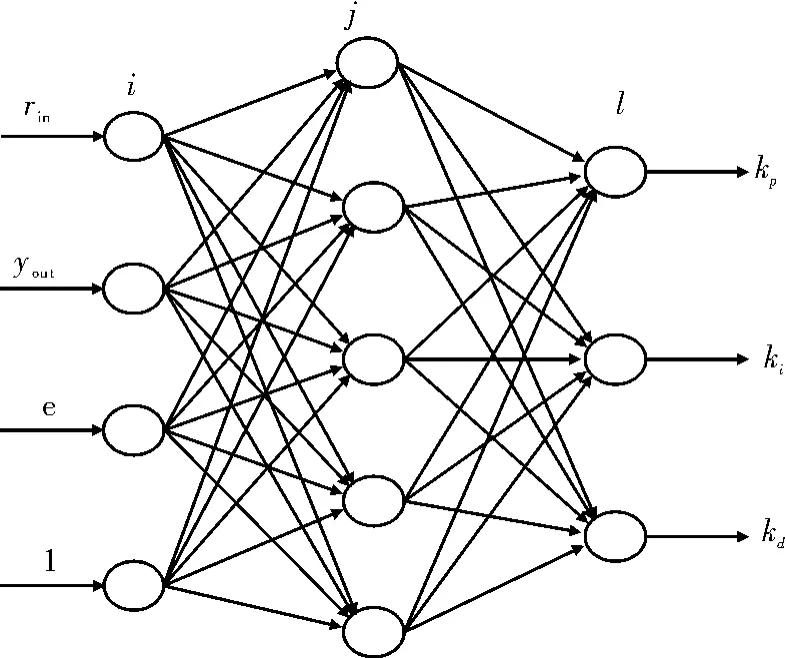
图2 BP 神经网络结构图
将粒子群优化算法的全局寻优能力与BP 神经网络的搜索思想相结合[7-8],既克服了寻优中的盲目性,也避免了局部收敛情况的发生。粒子群算法中的粒子由网络的权值和阈值组成,粒子的选择由群体极值来决定,从而通过适应度值对个体极值和群体极值不断的更新,最后得到最优群体极值对应的粒子,最终将选出的适应度最佳的个体值作为相应的BP 神经网络的连接权值和阈值。粒子群优化算法优化神经网络的流程如图3 所示。
2.3 改进的PSO 优化神经网络的PID 控制
将改进的BP 神经网络与PID 控制相结合[9],基于改进的BP 神经网络的PID 控制器结构如图4 所示。由图4 可知,改进的BP 神经网络的PID 控制系统由两部分组成:(1)PID 控制器:kp,ki,kd为在线调整参数。(2)改进的BP 神经网络:粒子群优化算法对神经网络的权值进行训练,获得最佳权值;神经网络在线调节PID 控制器参数,通过神经网络的自学习和自适应能力,实现系统的自适应控制。其算法主要步骤如下:
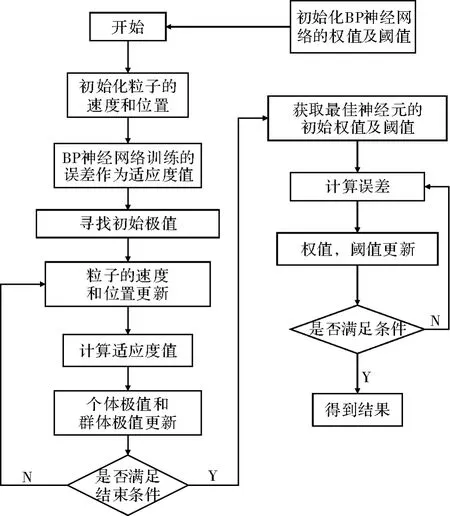
图3 粒子群算法优化的BP 神经网络流程图
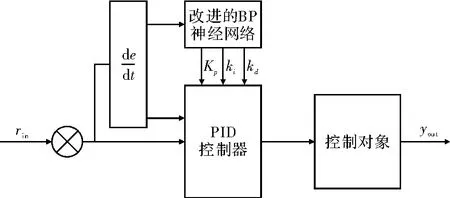
图4 改进的BP 神经网络PID 控制图
步骤1 用改进的粒子群优化算法对神经网络的权值进行训练,从而获得最佳权值。
步骤2 确定BP 网络的结构,确定各层节点数,根据(1)获得的最佳权值及神经网络各层的公式计算输入输出。得到的神经网络的输出,即是PID 控制器的参数。
步骤3 通过采样得到输入rin,得到输出yout计算误差error=yout-rin。
步骤4 通过神经网络的自学习能力,通过e(k)反传调整权值,从而实现PID 控制器的参数的自适应调整。
步骤5 控制系统若达到稳态,则此时误差已足够小,停止学习。否则,将不断调整学习算法的权值。
3 仿真与分析
对空气中PM2.5 的含量监测已成为衡量大气污染程度的重要手段,使用PM2.5 测量系统的用户也日益增多,将PM2.5 测量系统应用到室内灰尘的测量已成为一个趋势[10]。
PM2.5 测量系统由灰尘传感器输出模拟信号,信号经A/D 转换器后,经过单片机对信号进行采集、计算和处理后,通过USB 线或无线装置将PM2.5 的数值显示在电脑或LCD 显示屏上。
系统硬件由灰尘传感器、单片机、A/D 转换器和电源电路等部分组成,系统主要用于除尘设备、空气净化设备、除尘机器人、大气测量、烟气测量等领域,其系统组成框图如图5 所示。
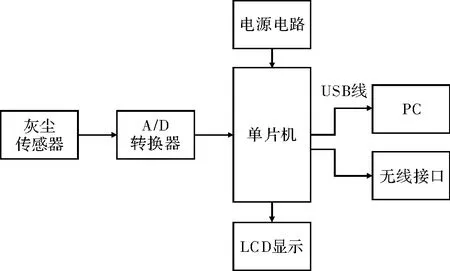
图5 PM2.5 测量系统框图
为验证PSO-BP-PID 算法对测量系统输出电压优化后的效果,分别用PSO-BP-PID 和传统PID 进行对比试验。
该研究PSO-BP 网络中,PSO 惯性系数w ∈[0.4,0.9],c1=c2=2,BP 网络结构为4-5-3,设定输入值为rin,输出值yout,输入层的加权系数的初始值是4×5 矩阵,隐含层的加权系数的初始值是一个5×3 矩阵,输出层的3 个输出值分别对应PID 控制器的kp,ki,kd。通过仿真验证,分别得到了优化前后系统输入信号及响应曲线和误差曲线的对比图。
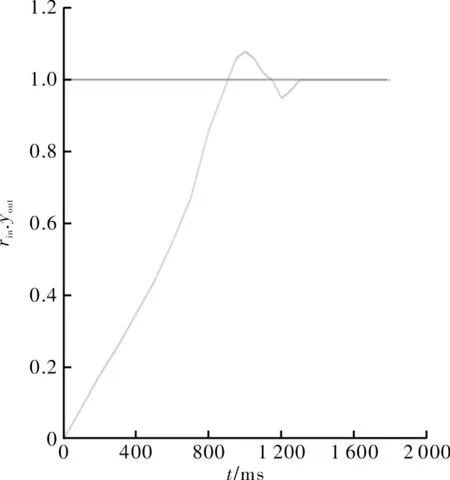
图6 系统输入信号及响应曲线(优化前)
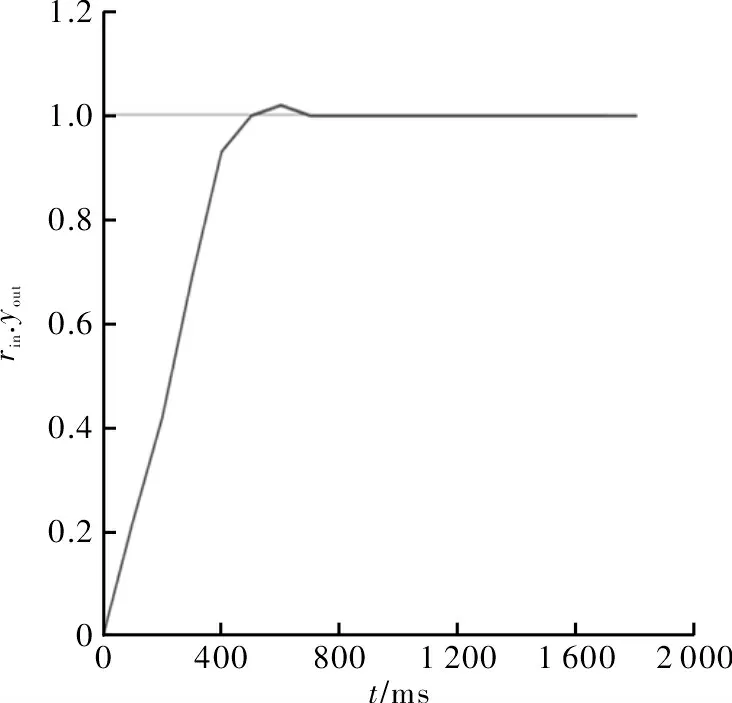
图7 系统输入信号及响应曲线(优化后)
由图6 和图7 对比可知,优化前,曲线有较大振动,优化后,在较短的时间内便可达到稳定状态,即优化后系统的性能得到了大幅改善;由图8 和图9 对比可知,优化前,系统误差可平稳减少,但优化后效果明显更好,优化后减少了输出的误差,提高了测量精度。
4 结束语
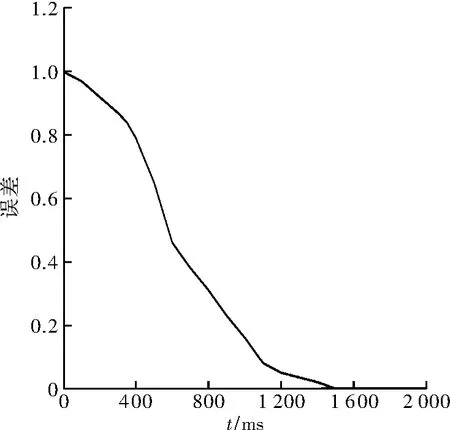
图8 误差曲线(优化前)
用PSO 算法优化BP 神经网络避免了其收敛性慢和易陷入局部最优的缺点,可快速找到全局最优解。针对PM2.5 测量系统的非线性,大延迟和大惯性的问题,运用BP 神经网络的自学习能力,自适应能力以及非线性系统任意逼近的特性,将改进的BP 神经网络与PID 控制器相结合,通过仿真表明,用改进的粒子群优化算法优化的BP 神经网络的PID 控制对测量系统进行优化,可明显提高测量精度。
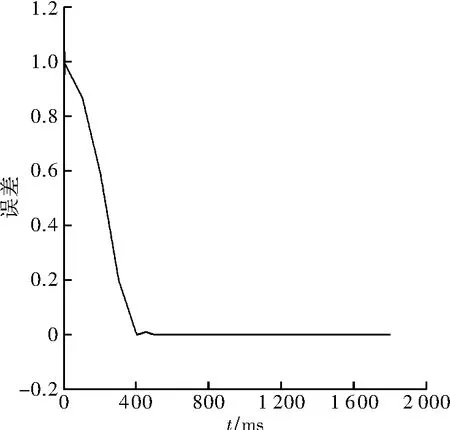
图9 误差曲线(优化后)
[1] 刘刚,刘学仁.基于递归神经网络的加速度传感器动态特性补偿[J].传感器与微系统,2007,26(7):70-72.
[2] 王军号,孟祥瑞.一种基于改进遗传RBF 神经网络的传感器动态特性补偿算法[J].传感技术学报,2010,23(9):1298-1302.
[3] 高群.物联网框架下PM2.5 高精度测试模型仿真分析[J].计算机仿真,2014,31(11):377-380.
[4] 赵鑫,潘晋孝,刘宾,等.基于β 射线吸收法的PM2.5 测量技术的研究[J].测控技术与仪器仪表,2013,39(9):74-76.
[5] 陶永华.新型PID 控制及其应用[M].北京:机械工业出版社,2002.
[6] 张德丰.Matlab 神经网络应用设计[M].北京:机械工业出版社,2009.
[7] 江丽,王爱平.基于粒子群与BP 混合算法的神经网络学习方法[J].计算机应用,2012,32(S2):13-15.
[8] 钱锋.粒子群算法及其工业应用[M].北京:科学出版社,2013.
[9] 任子武.高俊山.基于神经网络的PID 控制器[J].控制理论与应用,2004,23(5):16-19.
[10]刘银,廖志鑫,贺良茂,等.基于单片机的粉尘检测系统设计[J].煤矿机械,2011,32(7):240-243.
