同步磁阻电机混沌系统的自适应滑模控制
2015-03-06雷腾飞
雷腾飞,陈 恒,孟 敬,王 荣
(西京学院 控制工程学院,西安 710123)
同步磁阻电机是一种广泛应用的执行元件,具有转子内部不需要附加励磁且转换效率高、可靠性好等特点,但应用中发现存在混沌现象。当前,对电机混沌的研究主要集中在永磁同步电机系统,对同步磁阻电动机混沌属性控制的研究较少。文献[1-2]验证了风力发电系统中存在混沌现象;文献[3]分析了无刷直流电机发的混沌现象并做数值仿真;文献[4]成功实现了对无刷双馈风力发电机的H∞控制;文献[5],成功实现了对永磁同步发电机的控制,但不是对任意轨道的控制;文献[6]对永磁同步电机混沌系统提出了一种自适应控制;文献[7]对同步磁阻电机混沌系统混沌现象进行了分析,但是没有控制混沌状态;文献[8]建立了永磁同步风力发电分数阶模型并采用了自适应控制方法进行控制。本文根据同步磁阻电机的特点,提出了用滑模变结构控制,使系统脱离了混沌,克服其电机系统以往不能控制固定点的缺点。
1 同步磁阻电动机混沌系统模型
基于同步磁阻电动机混沌系统的模型为
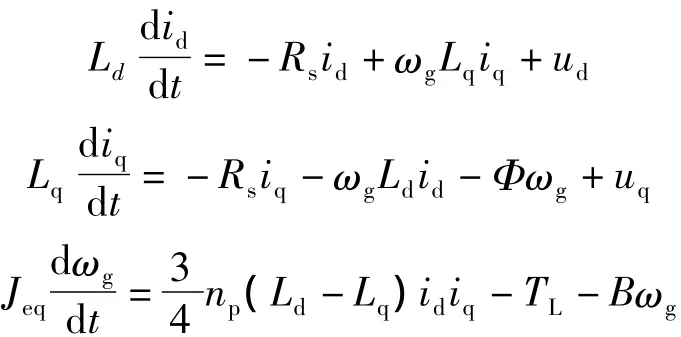
式中:id,iq与ud,uq分别为定子电流与电压的直轴与交轴分量;Rs为定子电阻;ωe,ωg分别为电角频率与发电机转速;Ld,Lq分别为直轴与交轴的电感;Jeq为机组等效转动惯量;Φ为永磁磁铁的磁通;Te为转磁转矩;B为发电机的转动粘滞系数。
假设发电机气隙均匀,d轴与q轴电感量相同,经过仿射变换与时间尺度变换得到的无量纲状态模型为
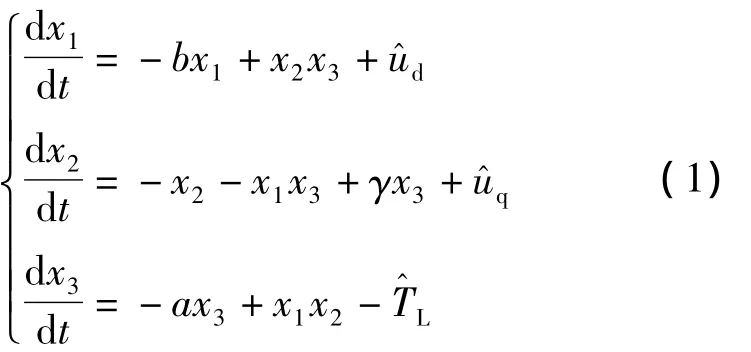

图1 同步磁阻系统的混沌吸引子Fig.1 Chaotic attractor of synchronous reluctance system
2 滑模控制器的设计
变结构控制理论的基本思想是利用高速切换开关控制,把受控的非线性状态轨迹引向一个指定的状态空间平面,随后系统的状态轨迹就限定在这个平面上了,这对系统参数的误差、参数变化以及外部扰动有很好的不敏感性。
系统(1)的受控形式为
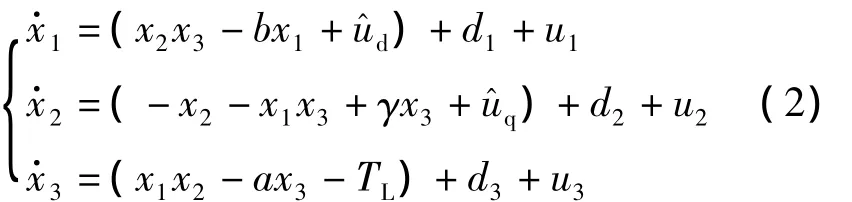
式中u1,u2,u3为控制输入。定义矩阵:
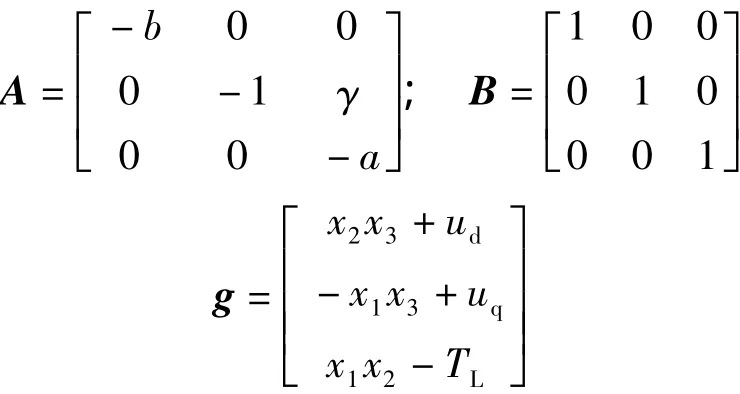
式中:A为同步磁阻电机系统线性矩阵;B为控制其系统的矩阵;g为系统的非线性矩阵。
系统的控制目标是使系统状态 x=[x1,x2,x3]T跟踪一个时变状态 xd=[xd1,xd2,xd3]T。基于此,可定义其跟踪误差为
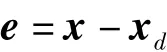
误差动力系统可写为
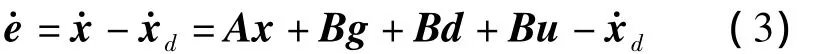
定义时变的比例积分滑模面S=S(e,t):

式中:附加矩阵 K∈R3×3且满足 det(KB)≠0,本文取 K=diag(1,1,1);附加矩阵 L∈R3×3且满足 A -BL为负定矩阵。在滑动模态下必须满足S==0,即为切换面。
为满足滑动条件,设计滑模控制器为
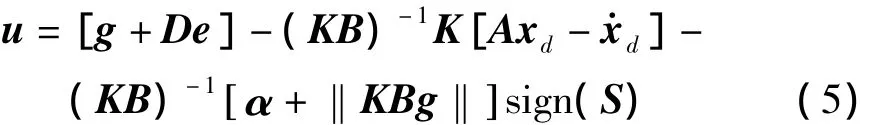
定理 若 ε满足 ε>δ+1,系统(2)在控制器(5)的作用下可以在有限时间内迅速达到滑动模态S=0,状态变量与参考状态xd轨迹一致。
证明 构造Lyapunov函数V=STS,带入式(3)~式(5),可得

同样的方法,可证
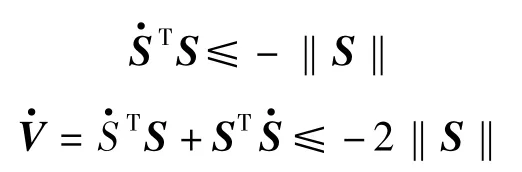
证毕。
上述证明说明同步磁阻电机混沌系统,在滑模变结构控制下能有效使处于混沌状态下的系统到固定点。
为了使得系统(2)控制到目标状态,设计附加矩阵K=diag(5,5,5),这样可保证 KB为可逆矩阵。选取A-BL的特征值为P=[-5,-5,-5],采用极点配置法确定矩阵为

选取比例积分滑模面为
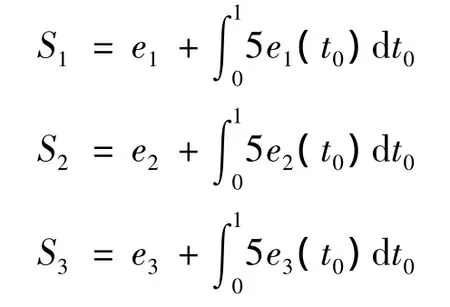
设置系统初始值(x1(0),x2(0),x3(0))=(1,1,1),控制系数 ε =5,参照状态 xd1=xd2=xd3=xd,则控制信号为

3 仿真结果
通过上面理论推导与计算,得出此控制方法能够控制系统(2)稳定到任意一点。为了验证该控制方法的有效性及不失一般性,本文取固定点(1,3,4.5),此时,选取xd=0.5,在2 s时加入控制器,运用Matlab得到了系统状态变量随时间变化图形如图2所示。此时系统参数取值为:u^d=0,u^q=0,T^
w=0,a=1.6,b=0.2,γ =10。当系统运行到 2 s时,加入控制项,系统迅速达到稳定状态,具有良好稳定性能。
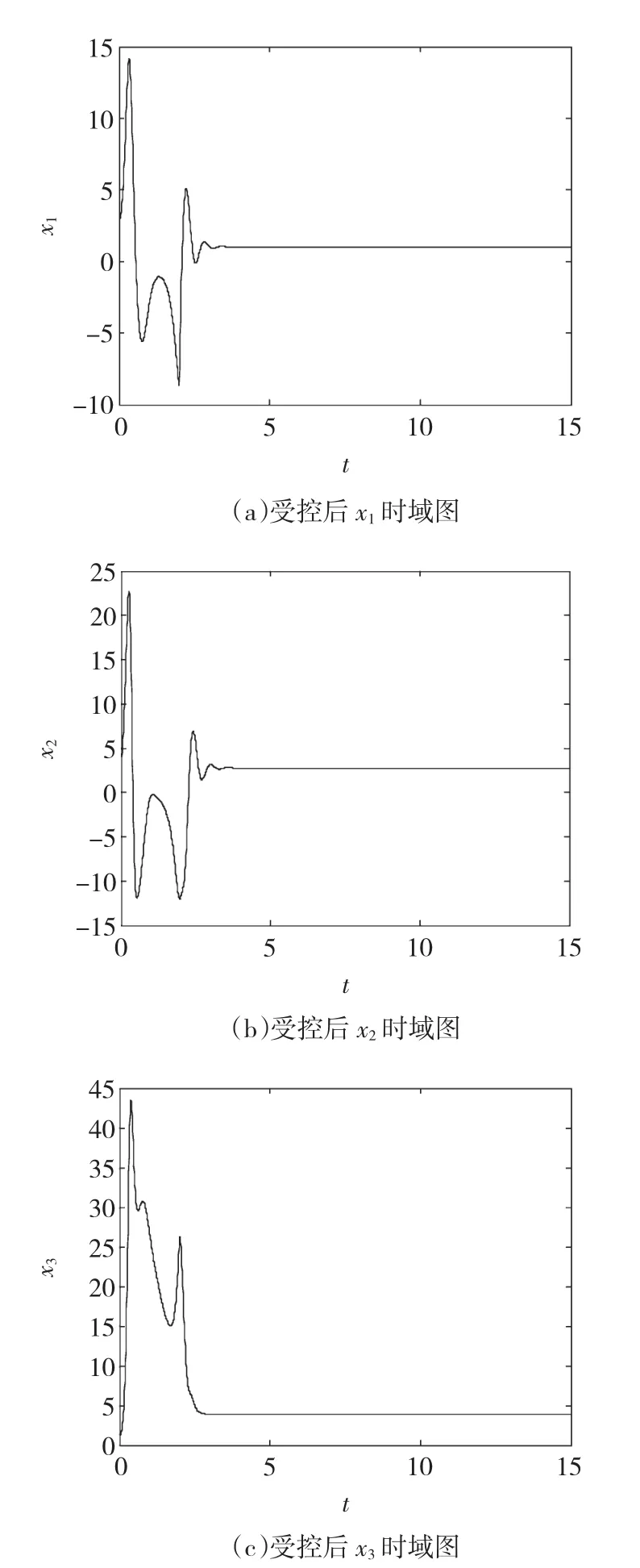
图2 参数未知受控系统的动态特性Fig.2 Dynamic characteristics of controlled systems with unknown parameters
4 结语
针对同步磁阻电机在特定条件下出现的混沌现象,提出一种系统控制方法,实现了同步磁阻电机混沌系统对任意给定初始值都可以控制到固定点。基于Lyapunov稳定性控制理论与滑模结构方法,设计了同步磁阻电机混沌系统的自适应滑模控制器,有效抑制和消除电力传动系统中的混沌现象,保证了系统的稳定运行。
[1] 安学利,蒋东翔.风力发电机组运行状态的混沌特性识别及其趋势预测[J].电力自动化设备,2010,30(3):13-24.AN Xueli,JIANG Dongxiang.Chaotic characteristics identification and trend prediction of running state for wind turbine[J].E-lectric Power Automation Equipment,2010,30(3):13 -24.
[2] 张波,李忠,毛宗源,等.一类永磁同步电机混沌模型与霍夫分叉[J].中国电机工程学报,2001,21(9):13 -17.ZHANG Bo,LI Zhong,MAO Zongyuan,et al.The chaotic model and Hope bifurcation of a type of permanent-magnet synchronous motor[J].Proceedings of the CSEE,2001,21(9):13 -17.
[3] 杨志红,姚琼荟.无刷直流电动机系统非线性研究[J].动力学与控制学报,2006,4(1):59-62.YANG Zhihong,YAO Qiongyun.Research of non- linearity in brushless dc motor system [J].Journal of Dynamic and Control,2006,4(1):59-62.
[4] 蔡超豪.无刷双馈风力发电机的H∞控制[J].电机与控制应用,2011,38(3):45 -50.CAI Chaohao.H∞control for brushless doubly-fed wind generator[J].Electric Machines and Control Application,2011,38(3):45-50.
[5] 杨国良,李惠光.直驱式永磁同步风力发电机中混沌运动的滑模变结构控制[J].物理学报,2009,58(11):7552 -7557.YANG Guoliang,LI Huiguang.Sliding mode variable- structure control of chaos in direct-driven permanent magnet synchronous generators for wind turbines[J].Acta Physica Sinica,2009,58(11):7552-7557
[6] 张兴华,丁守刚.非均匀气隙永磁同步电机的自适应混沌同步[J].控制理论与应用,2009,26(6):661 -664.ZHAGN Xinghua,DING Shougang.Adaptive chaotic synchronization of permanent magnet synchronous motors nonsmooth airgap[J].Control Theory & Applications,2009,26(6):661 -664.
[7] GAO Y,CHAU K T.Hopf bifurcation and chaos in synchronous reluctance motor driver[J].IEEE Transaction on Energy Conversion,2004,19(2):296 -302.
[8] 雷腾飞,陈恒,王震,等.分数阶永磁同步风力发电机中混沌运动的自适应同步控制[J].曲阜师范大学学报:自然科学版,2014,40(3):63 -68.LEI Tengfei,CHEN Heng,WANG Zhen,et al.Adaptive synchronization control of chaotic motion in fractional order permanent magnet synchronous wind generators[J].Journal of Qufu Normal University:Science and Tehcnology,2014,40(3):63 -68.
