基于倍角三角形的一类一元高次方程求解

王雪茹，赵继伟

（西北大学数学与科学技术史研究中心，陕西西安710127）

基于倍角三角形的一类一元高次方程求解

王雪茹，赵继伟

（西北大学数学与科学技术史研究中心，陕西西安710127）

研究韦达构造倍角三角形的一般方法，总结出n倍角三角形正余弦与单倍角三角形正余弦之间的关系，并根据这种关系，给出一类特殊的一元高次方程的解法。

倍角三角形；余弦公式；高次方程求解

高次方程的求解在数学史上具有重要的地位。长期以来，数学家们发明了很多种数值算法来逼近方程的实根。法国数学家韦达(Francois Vieta, 1540—1603)从研究倍角三角形入手，发现了n倍角展开式和高次方程之间的关联，一度解决了一个特殊的45次方程。

本文通过研究韦达关于倍角三角形的构造方法，推导出一般n倍角正余弦公式，并且通过n倍角正余弦①正余弦：本文中所有出现的正余弦在韦达所在的时期都没有，韦达对正弦的表示是直角三角形中高与斜边的比，余弦也表示为底边与斜边的比，本文为方便理解引入我们今天所用的正余弦的概念及表示方法。与单倍角正余弦之间的恒等关系，研究满足一类特殊系数的一元高次方程的求解。韦达就曾用此方法解决了比利时数学家罗马努斯（Adriaen van Roomen，1561—1615）提出的45次方程的解[1]208。笔者还将给出可求解的这一类一元高次方程的系数表,用来验证所给出的高次方程是否可以用这种方法求解，如果系数满足表中数字，则可以按照这种方法给出其解答。

1 倍角三角形构造

法国数学家韦达，在他从事律师职业期间研读了卡尔丹、塔塔利亚、邦贝利、斯蒂芬和丢番图等数学家的著作[2]129。《分析术》(The analytic art)是T.Richard Witmer整理翻译韦达在1584年左右的几篇著作，其中包括《分析术引论》(Introduction to the analytic art)、《符号运算法则》（Preliminary notes to symbolic logistic）、《角分割的一般定理》(Universal theorems on the analysis of angular sections)等8部分[3]9-10。

在《符号运算初步》中韦达利用两个已知直角三角形构造第三个直角三角形，并且满足第三个直角三角形的底角是已知直角三角形底角之和或之差，推导出第三个三角形三条边与已知直角三角形三条边之间的关系[4]。具体构造方法如下：已知两个直角三角形，斜边分别为Z,X，高分别为B,F，底边分别为D,G，底角分别为∠a和∠b，如图1所示。

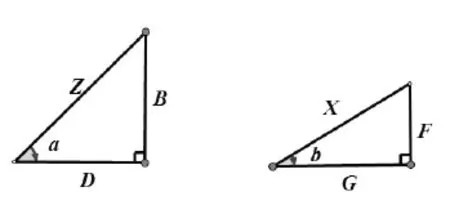
图1 已知直角三角形

根据两角之和的正余弦公式可得，构成的第三个直角三角形的底角是两个已知直角三角形的两底角之和，它的斜边相似于第一个直角三角形的斜边与第二个三角形斜边的乘积，称之为ZX，高相似于第一个三角形的高与第二个三角形底边的乘积，加上第一个三角形的底边加上第二个三角形的高，即BG+DF，底边相似于两个三角形的高的乘积与两个三角形底边乘积之差DG～BF。相应的根据两角之差的正余弦定理可得，构成的第四个三角形的底角是两个已知直角三角形的底角之差，它的斜边相似于ZX，高相似于DG～BF，底边相似于DG～BF。具体如图2所示，前者称为合角三角形，即它的底角是已知直角三角形的底角之和；后者成为分角三角形，即它的底角是两个已知直角三角形的底角之差。

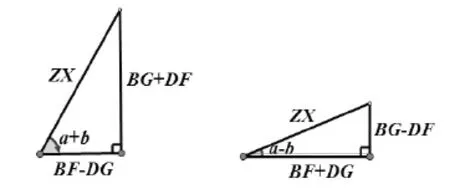
图2 合角三角形及分角三角形

按照合角三角形的构造方法，设两个全等的直角三角形斜边为A，底边为D，高为B，构造第三个直角三角形。那么按照上面给出的合角三角形三边满足的关系可知：构造的新的直角三角形的底角是已知两个三角形底角的之和，也就是已知全等三角形底角的2倍，它的三条边满足：斜边相似于已知直角三角形两条斜边的乘积，即A2；底边相似于已知的直角三角形底边的乘积与高的乘积之差，即D2～B2；高相似于第一个直角三角形高与第二个直角三角形底边的乘积加上第一个直角三角形底边与第二个直角三角形高的乘积，即2BD。如图3所示。其中二倍角三角形的斜边、底边及高分别相似于：

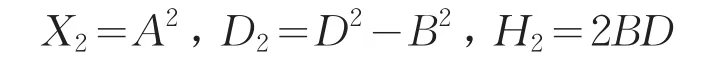
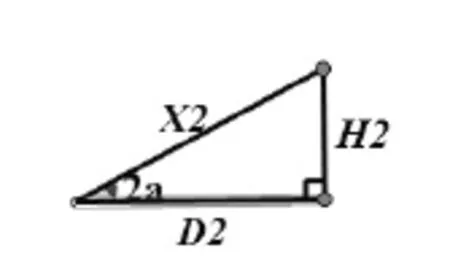
图3 二倍角三角形

同理，单倍角与二倍角之间使用合角三角形的方法，可得三倍角三角形三边分别相似于：

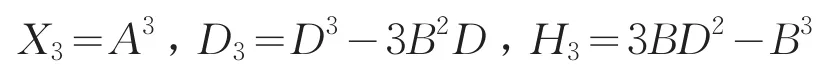
四倍角三角形三条边分别相似于：

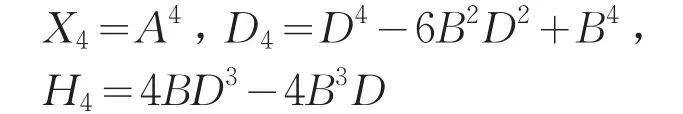
五倍角三角形的三条边分别相似于：

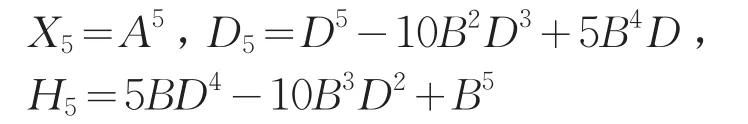
从上面的推导过程我们可以得到如下的一般规律：n倍角三角形的斜边相似于A的n次幂，对应的底边与高的组成项都是二项式（D+B）n的n+1个展开项，项按照D的幂次从大到小排列，其中第1、3、5等项组成底边，并且正负相间；第2、4、6等项组成高，并且正负相间[5]。这样便给出了一般n倍角三角形三条边之间的比例关系，或者说在一定意义上给出了n倍角正余弦公式。

2 一般n倍角余弦公式

根据上面给出的n倍角三角形三边之间的关系式可得：

总结一般n倍角三角形的恒等式为：

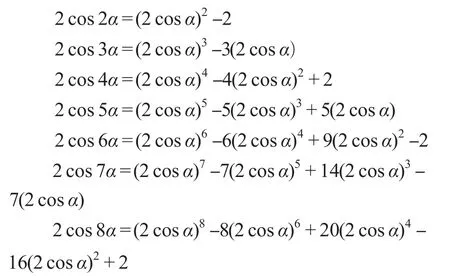
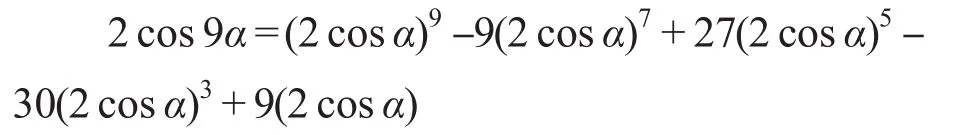
按照上面的公式推导可得2cosnα关于2cosα的表达式，用表1表示系数绝对值。表1中的数字满足：an,m=an-1,m+an-2,m-1这样的关系，所以按照这样的关系可以一直做下去，得到n倍角三角函数的恒等式系数。

3 高次方程求解

1593年，时任荷兰大使的比利时数学家罗马努斯（Adriaen van Roomen，1561—1615）向法国国王亨利四世提出的了一个45次方程

x45-45x43+945x41-12300x39+…-3795x3+45x=C并宣称法国无人能解。韦达发现这是一个关于类似于正弦函数的恒等式，并给出C=2sinα则这样的一个解，随后他给出这个式子的所有的23个正解，即，韦达还指出

这个方程还可以有22个负解，不过他本人并不接受负数，但是在一定意义，韦达解决了这个45次方程。

上面是韦达给出的对于这样的45次方程的解，按照韦达的思想换个方式来做。令C=2cos45α，按照上一节给出的公式，满足

很容易发现45倍角的余弦定理中的系数与方程中的系数一致，并且相邻的幂也相差两次，我们可以直接给出方程的根为

表1 n倍角余弦公式系数表

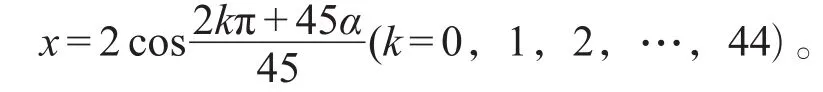
从这个方程的解得出：所有满足n倍角正余弦公式系数及幂的方程，都可以按照代入正余弦恒等式的方法求解，这类特殊高次方程的系数可以参照表1的数字，如果满足其中的某一关系就可以用这样的方法求解。

笔者给出一个例题：求解下面的11次方程，

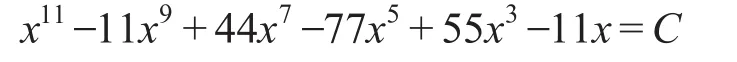
观察发现这个方程的系数满足表中11倍角的余弦恒等式的系数，相邻未知数的次数也是相差两次，且未知数对应系数的符号正负相间，所以按照这样的方法，可以令C=2cos11α相应的可以给出满足x=2cos(k=0，1，2，…，10)的一组解，由于k有11个不同的值，所以这样的方程就有11个不同的解。

多倍角余弦定理的恒等式，为我们处理这一类高次方程提供了直接简单的方法。在我们遇到一个高次方程求解的问题时，我们可以把这样的方法当作一种判定的条件，如果满足上面的条件，或者适当变换后满足上面的条件，我们可以直接使用上面的方法给出答案，反之则需要我们再去寻找其他的方法。

4 结论

本文通过对《分析术》中的研究，总结了韦达构造合角三角形的一般方法，并由此推出倍角三角形三条边之间的关系，总结一般余弦公式，并且给出的一类特殊高次方程的求解方法，即所有满足xn-axn-2+a1xn-4-…=C类型的一元高次方程，相邻未知数次数相差2个，方程系数正负号间隔出现，且系数满足表中某一行的系数关系，则这类方程可用上面的方法求解。

[1]UTA C M,CARL B B.A history of mathematics[M].Thired edition.Hoboken:John Wiley&Sons.Inc.2010.

[2]李文林.数学史概论[M].2版.北京：高等教育出版社，2002.

[3]FRANCOIS V.The analytic art[M].Translated by T.Richard Witmer.New York:Dover Publications Inc，2006.

[4]FRANCOIS V.Ad logisticem speciosam notae priores[J].G. Baundry,1631(82)：13-41.

[5]IAN B.A translated account of viète's ad angulares sectiones [EB/OL].[2015-03-08].http://www.17centurymaths.com/ contents/Angular%20Sections.pdf,.

Find the Solution for One Kind of Higher Degree Univariate Polynomial Equation Based on the Multiple-angle Triangle

WANG Xueru,ZHAO Jiwei
(Center for the History of Mathematics and Science,Northwest University,Xi’an 710127,Shaanxi,China)

Based on the research of Francois Viete’s general method for construction of multiple triangle,summarized the relationship of sine and cosine formula between multiple angle and single angle.At last set out the solution for one kind of higher degree univariate polynomial equation.

multiple-angle triangle;cosine formula;the solution for equation of higher degree

N09

A

1672-2914（2015）02-0021-03

2015-02-14

国家自然科学基金项目（11171271；11001217）。

王雪茹（1989-），女，陕西蓝田县人，西北大学数学与科学技术史研究中心硕士研究生，研究方向为古代数学史。

：赵继伟，副教授，E-mail：553881072@qq.com。