明甪直天王殿松木斗拱振动台试验研究

阙泽利，李哲瑞，张贝贝，侯同宇，潘 彪

（南京林业大学 木结构建筑系，南京 210037）

明甪直天王殿松木斗拱振动台试验研究

阙泽利，李哲瑞，张贝贝，侯同宇，潘 彪

（南京林业大学 木结构建筑系，南京 210037）

以甪直保圣寺天王殿斗拱为参考对象，进行无缩尺松木斗拱模型的地震台试验研究。通过对斗拱的加速度与动力放大系数变化趋势、斗拱在振动过程中位移响应变化特征、斗拱变形最大时刻和各构件变形最大时刻的滑移位移和回转位移数值对比分析，得出以下结论：地震加速度用于衡量地震烈度，并不能直接反映斗拱试件的最大变形；振动频率的变化对斗拱回转变形的变化起重要作用，振幅是决定各构件水平滑移的主要因素；各构件变形最大值与斗拱整体变形最大值具有很强相关性，其中栌斗和华拱的回转变形对斗拱的整体变形而言，处于支配地位；斗拱的华拱连下昂部分主要起装饰作用，其榫卯连接节点位置在振动过程中较为薄弱，在对实际文物维护修缮过程中应引起重视并采取相关加固措施。

木结构；斗拱；松木；振动台试验；抗震机理

斗拱是中国古代建筑中的重要构件，它的演变是中国传统木构架建筑形制演变的重要标志。作为结构与立柱之间最重要的过渡部分，斗拱在建筑中起着受力和装饰的双重作用，特别是在减震吸能方面，作用更加突出。

斗拱整体可看作以横木交叠形成伸臂受弯压的梁垫，竖向可压缩变形，竖直向平面内可转动，水平层间可滑移，倒置的弹性固定铰支座［1］。从结构角度，斗拱从两个方向悬挑，减少了上部结构跨度，提高了梁、枋的承载能力，也使建筑物出檐更加深远，造形更加优美、壮观［2］；斗拱之间各构件互不粘连，而是由许多木构件通过榫卯咬合而成，以其特有的重叠伸张形式，垫在梁架层和柱额层之间的节点处，在水平地震力作用下，形成了梁柱间延性较好的节点，具有较大的弹塑性变形能力及摩擦耗能的减震作用［3］。

目前，中国古建筑研究已经从少数先驱者的惨淡经营进入了百家争辉的局面。由于古代木结构建筑的抗震性能比较突出，不少专家学者对古建筑及斗拱单元进行了竖向单调加载试验［2－4］、水平低周反复加载试验［4－6］及动力特性试验［7］等，并建立了力学模型［8－9］。中国学者对于木结构斗拱抗震性能的研究对象主要包括宋式斗拱和清式斗拱两种类型［10］，而对其他过渡时期的斗拱形式研究极少。试验中多选择经简化对称的斗拱模型为研究对象，未充分考虑实际斗拱在出跳方向由于华拱及下昂组合带来的不对称性对其稳定性造成的影响；大部分斗拱试件为缩尺模型，且很少作为独立单元进行试验；而从木材材性的角度对比分析斗拱的抗震性能的差异方面还鲜有研究。

试验选取明末苏州甪直镇保圣寺天王殿柱头科斗拱作为研究对象，参考久家英夫等［11］对足尺斗拱模型进行的振动台试验和分析方法，将斗拱作为独立试验单元，通过建立无缩尺模型的模拟振动台试验，分析斗拱的形态变化和抗震机理，探寻结构失效的原因与薄弱环节，对现存古建筑实例的维护与修缮起到一定指引作用，并为明代斗拱抗震性能的研究积累可靠数据。

1 试验材料与试验方法

天王殿位于苏州甪直镇保圣寺内，大殿坐北朝南，面阔三间，计11米有余。天王殿的斗拱用“四铺作插昂”造，厢拱上托挑檐枋直接承椽，犹存古制。斗拱的分布：平身科明间两攒，次间一攒，明间每攒当约合十五斗口。柱头科与平身科采用同样比例，于坐斗科斗口出一翘承载月梁。角科尚存下昂，于坐斗后出一翘，置于昂身下，中间施以“鞾楔”，手法与苏州松江两地明代所建东岳庙整点斗拱相近［12］。

据考原天王殿柱头斗拱用材为杉木，根据GB50165-1992《古建筑木结构维护与加固技术规范》第6.3.1条规定：古建筑木结构承重构件的修复或更换，应优先采用与原构件相同的树种木材，当确有困难时，也可选取强度等级不低于原构件的木材代替。考虑古代杉木材性与现代杉木速生材材性差异较大，因条件限制，无法取原天王殿柱头斗拱杉木材料进行力学性质测定，笔者选用强度等级高于现代杉木的花旗松（Pseudotsuga menziesii）为材料制作斗拱模型。模型试件的基本力学性能测定结果参见表1。

表1 材料的力学性能Table 1 Mechanical properties of materials

振动台试验依据苏州甪直保圣寺天王殿柱头斗拱构造形制，基于振动台尺寸和负荷能力考虑，设计制作无缩尺模型。模型总高613 mm，重48.9 kg，构件尺寸详见表2。模型构件由斗底至梁枋以下的两跳斗拱组成；各结构层之间按照实际使用要求，采用直榫连接；上部散斗分别安置木梁并找平，并在梁上安置水平配重板。由于振动台负荷能力受限，本试验拟在近似空载状态下进行，总配重45 kg，主要在振动过程中起平衡作用。

表2 模型构件尺寸Table 2 Size of test model components mm

斗拱试件组装完毕后，在栌斗处由定制铁箍固定在振动台上，如图1所示。在台面、栌斗底部和斗拱组顶部分别放置横向加速度传感器，将采集信号传送到振动台抗震抗剪测试分析系统。分别在栌斗、华拱连下昂的连接节点两侧布置竖向位移传感器测定其竖向绝对位移，在模型各层其他构件之间沿振动方向两侧布置竖向位移传感器测定其竖向相对位移；在栌斗底端及慢拱顶部布置横向位移传感器分别测定斗拱底部和顶部的水平绝对位移；其他构件连接处布置横向位移传感器测定各结构层间及斗与拱的相对位移。测点位置参见图2。通过测定斗拱各构件在振动过程中的水平及竖向位移变化，逐层计算叠加得到各构件回转变形及滑移变形值。

图1 栌斗及位移传感器固定细部Fig.1 Fixation of the Ludou component and displacement sensers

图2 回转及滑移位移测点布置图Fig.2 Arrangement of rotary and slip deformation measuring points

按照加载方案分为15组进行水平单向振动台试验，振动方向沿斗拱出挑方向。由于试验设备仅能输入正弦波型，故参考已测定El-centro地震波的特征频率和振幅范围［13］设定振动参数，通过控制振动台振动频率与振幅，模拟不同地震烈度的最大加速度振动工况。对试件依次进行由振动频率（电动机频率）10、15、20、25、30 Hz（振动台的振动频率相应为1.05、1.59、2.10、2.65、3.12 Hz），振幅10、20、30 mm组合的持续时间为30 s的地震模拟横向加载震动。各组工况相应的编号为P1010（前二位数值表示频率10 Hz，后二位数值表示振幅10 mm，下同）、P1020、P1030、P1510、P1520、P1530、P2010、P2020、P2030、P2510、P2520、P2530、P3010、P3020、P3030。

图3 振动台试验模型Fig.3 The model of shaking table test

振动台试验模型如图3所示。主要试验设备包括：四自由度模拟地震实验台（南京贺普科技有限公司）型号 HPDZ- 1；震动与动态信号采集分析系统（南京贺普科技有限公司）型号HPU100-F。

2 试验现象及结果分析

2.1 试验现象

当台面输入不同强度的振动激励时，斗拱整体表现较为均一的振动特征。其中在台面输入频率振幅均较低时，斗拱试件仅发生微小振动，并未产生明显倾角或滑移；当输入频率较低而输入振幅增至20 mm及以上时，结构产生较明显晃动，在华拱及下昂连接处出现可见倾角和滑移，在P1530工况时结构摆动最为激烈，栌斗斗耳及华拱与下昂连接处挤压发出吱吱声；随着台面输入振动频率继续增大，整体结构的摆幅减小，振动趋于规律。从宏观角度，模型在持续的往复振动过程中以构件节点转角变形为主，未出现明显的摩擦滑移。整个试验过程未出现构件局部破坏，但经过转角位移和水平滑移的叠加，在梁下慢拱处的水平绝对位移显著增大，最大滑移量约12 mm。

上述现象表明斗拱主要通过转动耗能来起到减震和隔震作用。由于栌斗下部固定在台面上，在振动过程中部分限制其转角和滑移，而上部结构的转动和滑移反向作用，在泥道拱和栌斗连接处对斗耳产生明显的挤压。且通过观察发现，因木材本身的湿胀干缩现象，在斗耳耳根处易产生裂缝，虽然在本试验中始终未出现构件的破坏，但若承载实际屋顶荷载的状态下振动，此处易产生剪切破坏造成斗拱整体失稳。由于与华拱连接的假昂部分仅依靠泥道拱与慢拱的相互挤压保持连接处的稳定，且下侧挑空缺乏辅助支承，在振动过程中尤为薄弱，并影响泥道拱与慢拱之间的连接紧密性。在泥道拱以上的慢拱和令拱部分则整体性较好，没有出现明显的滑移。

2.2 试验结果及分析

2.2.1 结构动力特征分析 根据所测斗拱组顶部与底部的加速度响应数值a，计算得到斗拱试件在不同工况下的动力放大系数β，β＝a1／a0，反映构件的隔振效果（参见表3）。

以烈度为基础进行抗震设计时，往往通过相应的峰值加速度来衡量地震强烈程度。但在同一加速度激励工况下，输入波形频率与振幅不同，试件的最大变形值也不同，说明加速度峰值并不能直接反映斗拱试件的最大变形。通过整理同振幅不同频率下模型动力放大系数变化趋势（参见图4）可以发现，1）在台面输入相同振幅条件下，随着振动频率的增大，模型动力放大系数逐渐减小。这是由于频率增大时，斗拱构件之间榫卯连接处摩擦加剧、斗与拱咬合处反复挤压耗能使减震作用增强；2）在输入相同频率条件下，随着振幅的增大，模型动力系数数值上有一定放大，且在台面振动频率值大于1.59 Hz（电动机频率15 Hz）时，相同频率下随振幅的增大动力系数值增幅明显减小，在振动频率达到2.65 Hz和3.12 Hz（电动机频率25 Hz和30 Hz）时，随振幅增大动力系数几乎不变。3）当台面振动频率低于1.59 Hz时，动力放大系数值大于1，且随振幅增大有显著上升。主要原因是在空载状态下由于斗拱本身层间摩擦较小，且无竖向位移限制，斗拱易产生大幅度摆动；又由于此时频率较低，斗拱的摆动也较为充分。这种情况在斗拱实际工作中很难出现。2.2.2 位移响应变化特征 通过整理试验各工况下斗拱试件各层的位移响应测试数据，绘制相应的位移变化曲线（以振动频率2.10～2.65 Hz工况为例，参见图5），分别选取栌斗、泥道拱及慢拱等主要构件，对比分析斗拱底部、中部及顶部的位移响应变化规律。

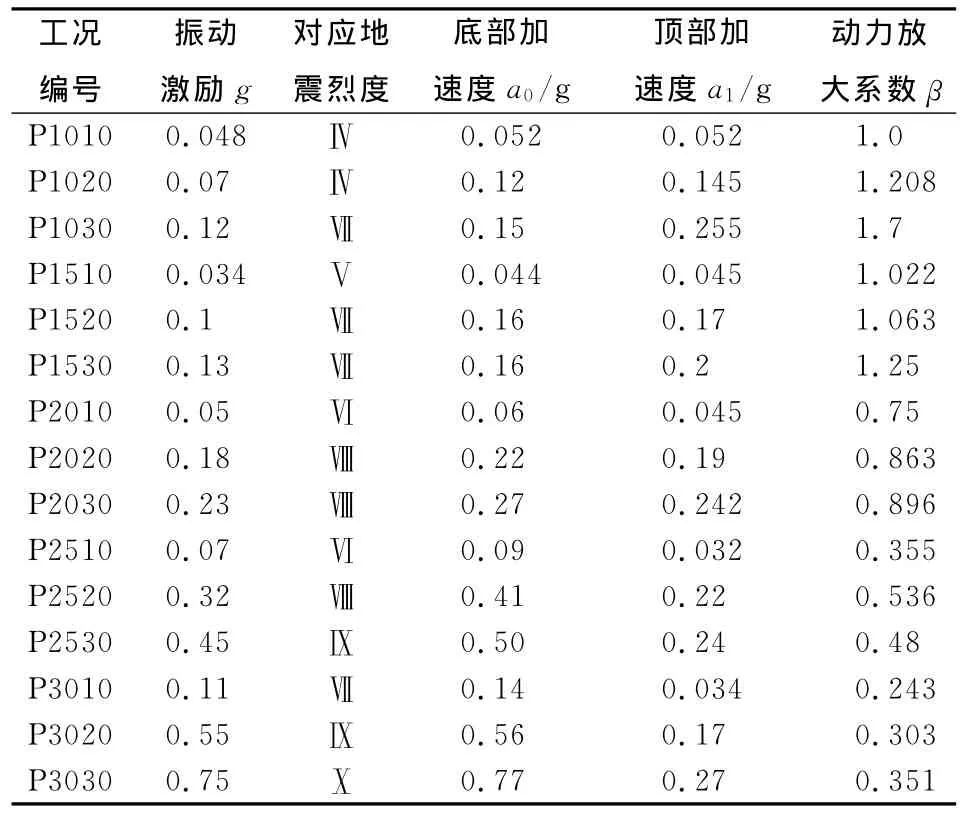
表3 加速度及动力放大系数Table 3 The acceleration and dynamic magnification coefficient

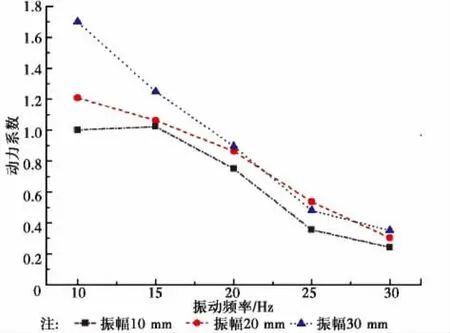
图4 同振幅不同频率动力放大系数变化趋势Fig.4 The change of dynamic magnification coefficient under same amplitude

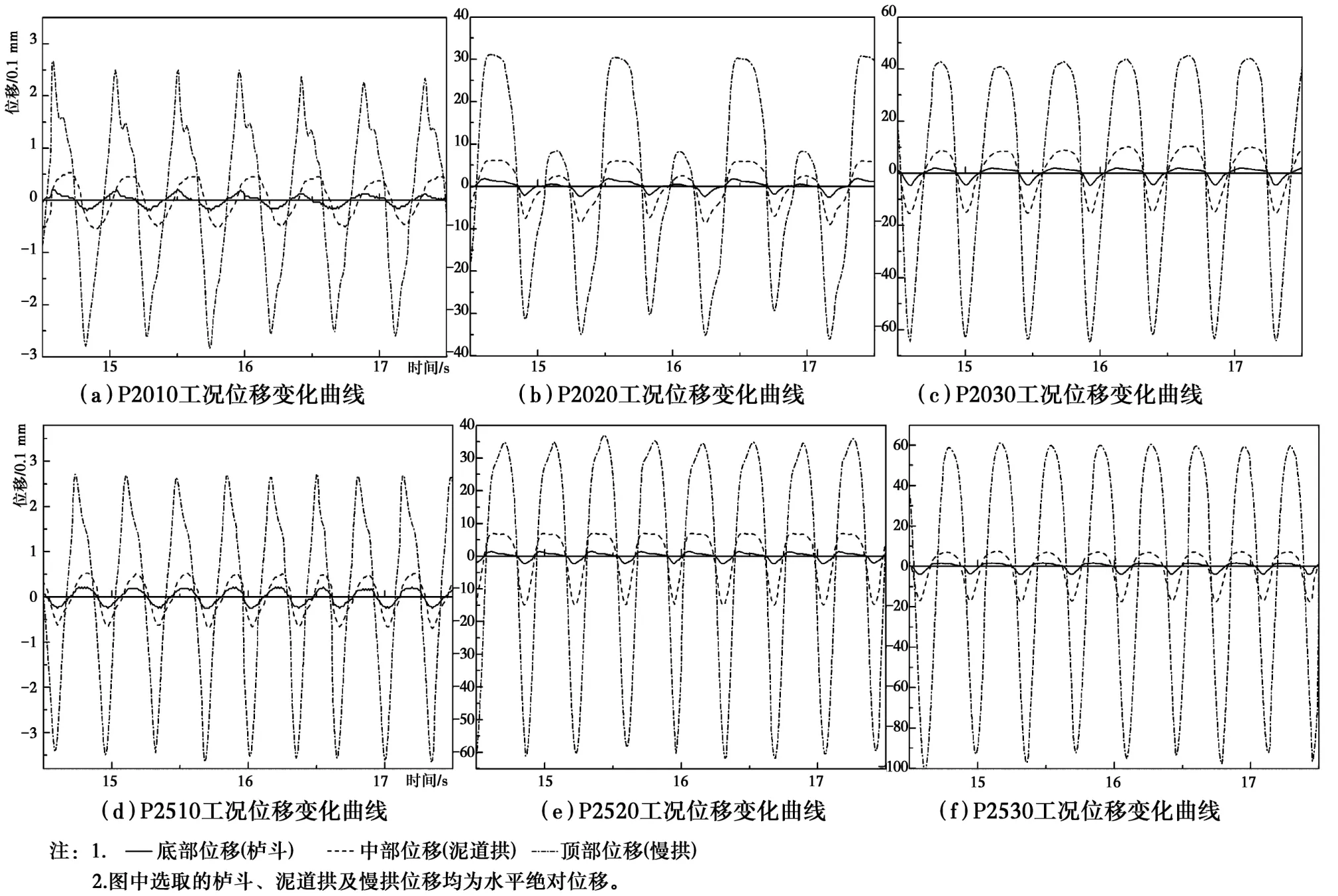
图5 20～25 Hz工况模型位移变化曲线Fig.5 Changing curve of displacement under 20 Hz and 25 Hz

从图5可看出：1）在反复加载振动过程中，斗拱的底部、中部和顶部振动位移曲线基本同步，说明试验中斗拱各构件间咬合状态良好，整体刚度保持较好；2）斗拱底部的位移波动幅度较小，随高度的增加波幅逐渐增加，在斗拱顶部位移达到最大。主要原因是在振动过程中斗拱中部主要构件如华拱、泥道拱等出现较大转角，并对斗拱整体位移向上叠加作用显著。另外由于顶部荷载较轻，在振动过程中其重心随斗拱摆动位置不断变化且相对滞后，对斗拱上部的水平位移提供了反向力的作用；3）相同振幅条件下，台面输入振动频率越大，斗拱所测构件水平绝对位移波形所体现的正弦波特征越明显；模型各层构件水平位移在P1530工况下达到最大值，其后随振动频率的增大，斗拱的水平位移反而有所减小。说明在一定范围内随振动频率的增大，斗拱层间摩擦及挤压变形的作用增强，有效限制了斗拱的摆动。4）在相同频率条件下，随着台面输入振幅的增大，泥道拱和华拱的水平绝对位移也随之增大。且不同频率状态下同振幅的位移基本不变，说明振幅是影响斗拱各构件水平向位移峰值的重要因素；由于栌斗固定在振动台台面上，限制了其水平方向的位移，而又因栌斗水平位移测点与台面间有一定距离，所以实际上测得栌斗水平方向位移主要是有其转角位移所致；5）斗拱试件依照天王殿柱头斗拱形制，其中华拱连下昂部分榫卯咬合拼装而成，并非单一构件，在振动过程中不但没有起到减震消能作用，反而在榫卯咬合部分出现较大倾角离缝，对斗拱整体结构造成额外负担。明代后期斗拱形制的变化趋势已由结构构件转向装饰构件，斗拱的减震消能作用明显削弱。此外需要说明，由于试验为空载振动试验，导致模型层间摩擦力和弹塑性变形受限，斗拱振动过程摆幅较大，因此，从图中看出斗拱上部位移的响应反而有所增大，但并非实际对地震动力响应的放大。2.2.3 回转位移与滑移位移 各工况下，斗拱组整体最大变形实测值、最大变形时刻与对应变形叠加值见表4。变形最大测量值指固定在斗拱组顶部的水平位移传感器测得的最大绝对变形值；最大变形叠加值为变形最大测量值相应时刻斗拱各层构件回转变形与滑移变形叠加获得。滑移位移和回转位移的叠加原理如图6所示。

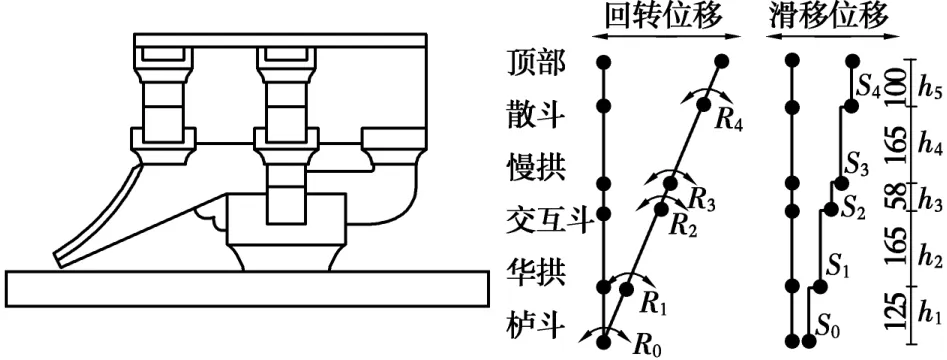
图6 斗拱组回转与滑移变形示意图Fig.6 Rotary and slip deformation for Dougong

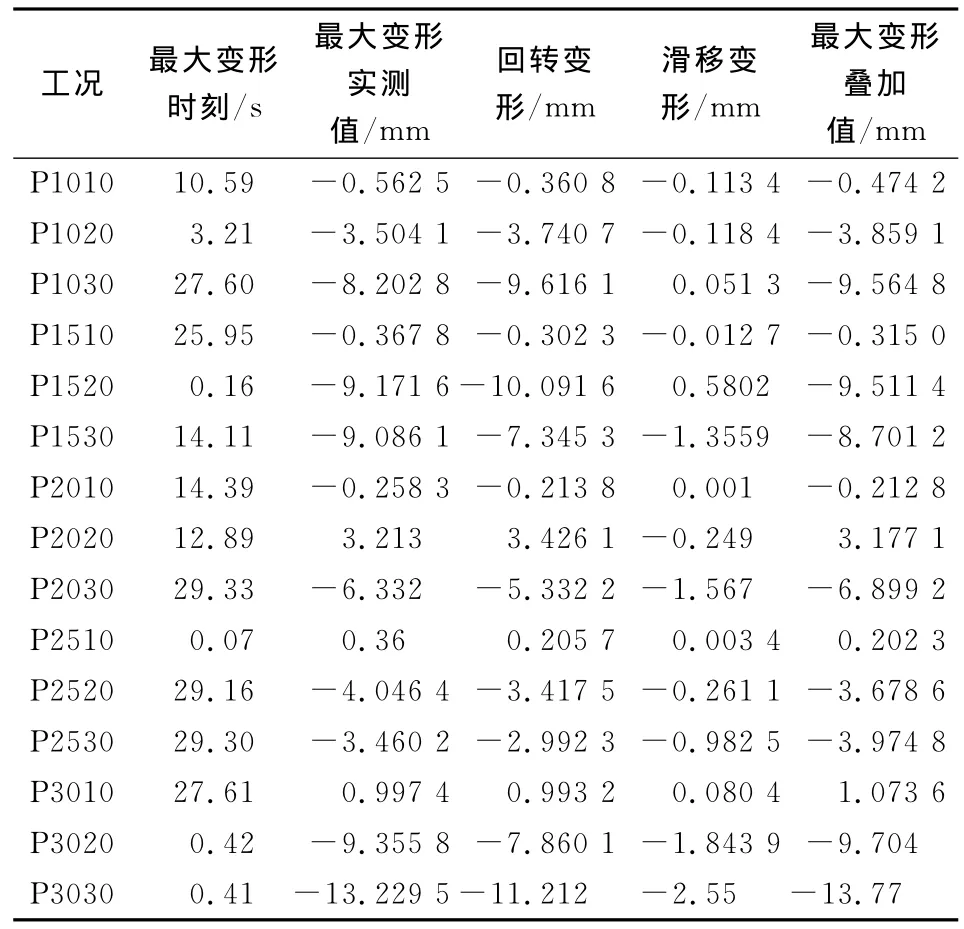
表4 各工况下斗拱组的变形值Table 4 Deformation value for Dougong of each condition

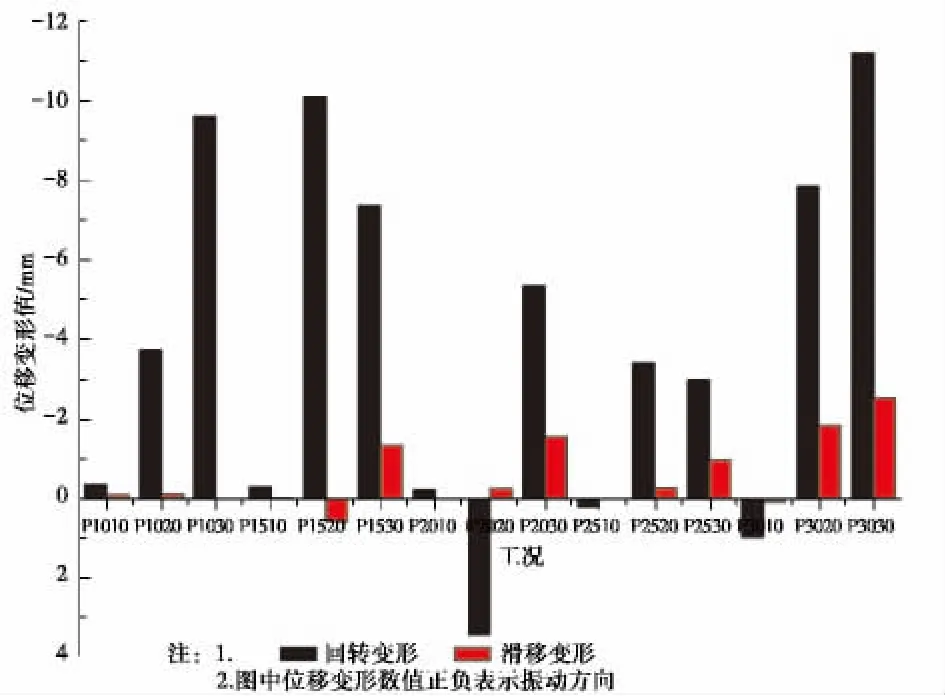
图7 各工况转角位移与滑移位移Fig.7 Rotary and slip deformation of each condition

由表4可知，通过水平滑移和回转位移的叠加求得的最大变形值与最大变形实测值基本吻合，说明本试验中采用的叠加计算方法是合理的；进一步将各工况下滑移变形和回转变形值进行对比，结合图7可以看出，最大位移的取得以回转变形位移为主；在低频状态下（1.05～1.59 Hz）随振幅增大回转变形位移明显增大，滑移位移始终较小；在频率上升至2.10～2.65 Hz时，回转变形位移值有所降低，且当振幅由20 mm升至30 mm时，回转变形位移几乎不变，滑移位移随振幅增大而逐渐增大；在高频状态（3.12 Hz）下随着振幅增大回转变形位移有较大幅度增长，并在P3030工况达到最大值；滑移位移的变化趋势基本未变。以上分析说明在振动过程中频率的变化对回转变形的变化程度起到重要作用，而对滑移位移的影响相对较小。

经过各构件试验数据的进一步整理，分别绘制各工况下斗拱变形最大时刻斗拱组各部分回转角和滑移变形与各部分回转角和滑移变形分别达到最大时刻表（以振动频率1.59 Hz条件下工况为例，参见表5至表10）。

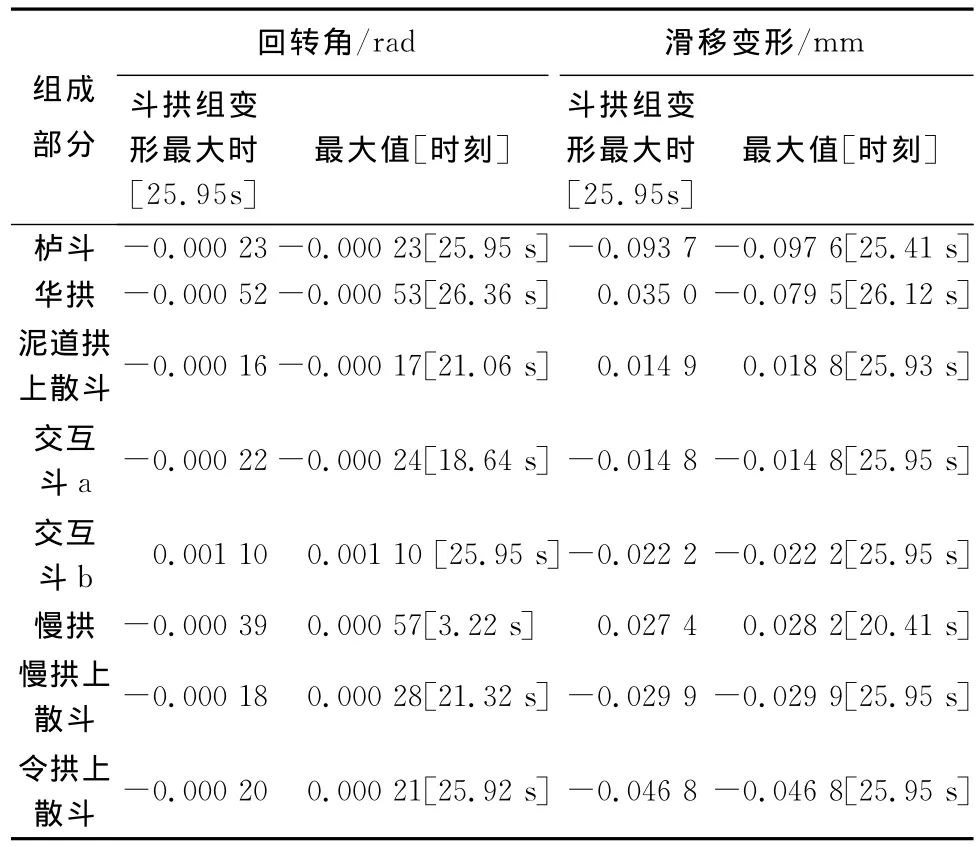
表5 P1510工况斗拱组各部分回转角和滑移值Table 5 Rotary and sliding displacement for Dougong each part in condition P1510

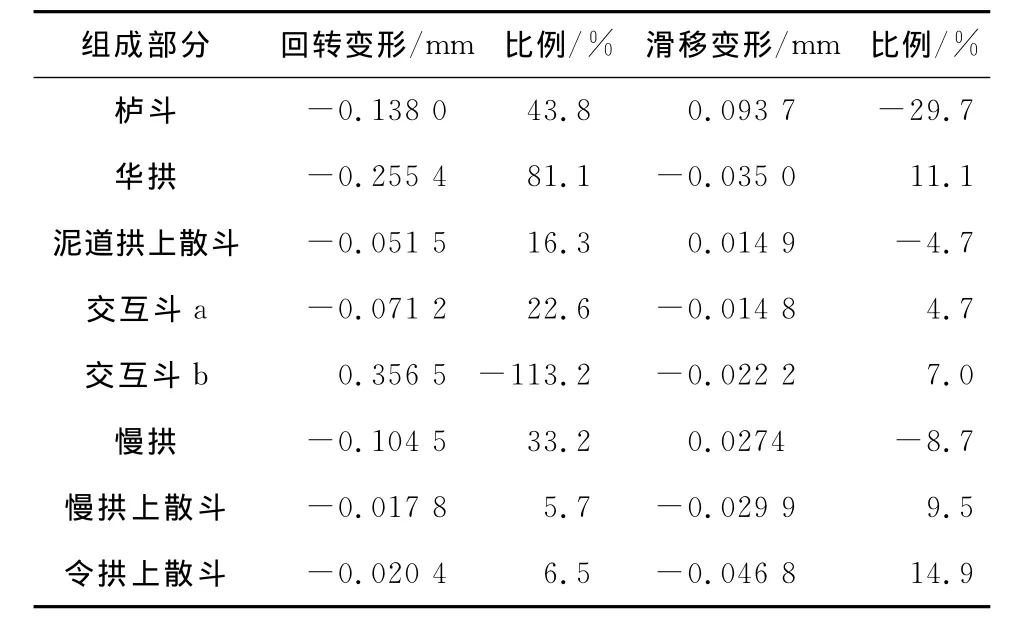
表6 P1510工况斗拱组各部分变形比例Table 6 Deformation scale for Dougong each part in condition P1510

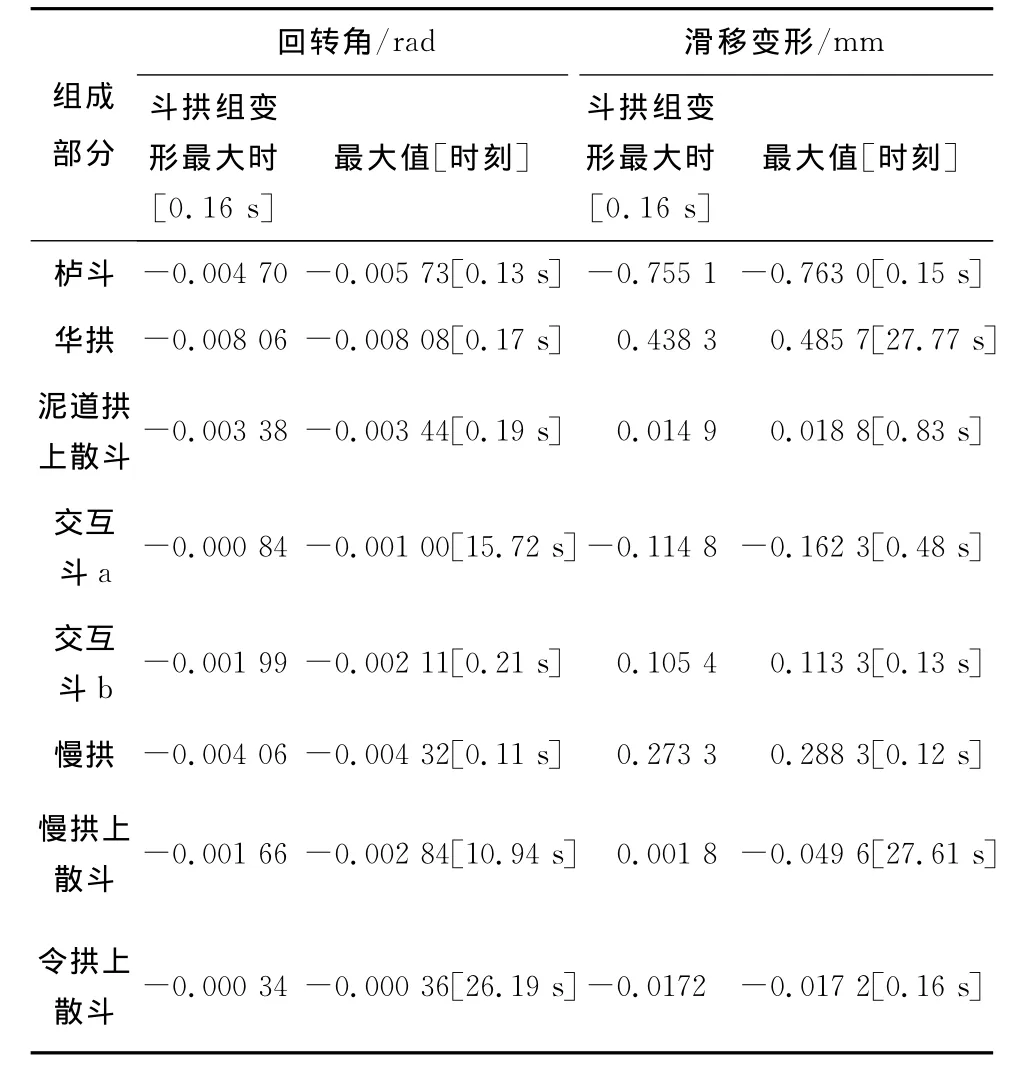
表7 P1520工况斗拱组各部分回转角和滑移值Table 7 Rotary and sliding displacement for Dougong each part in Condition P1520

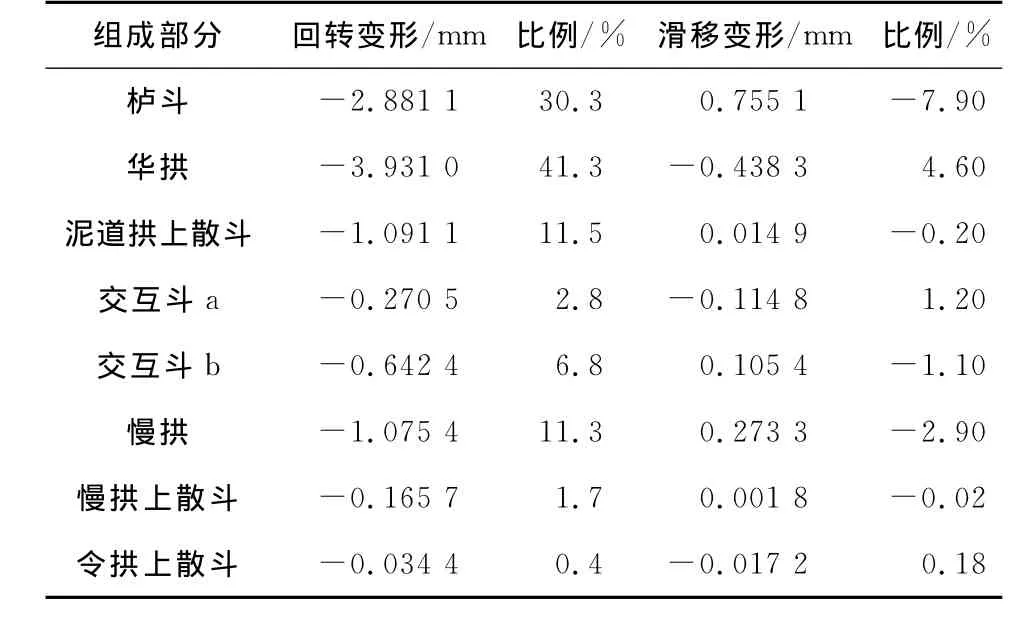
表8 P1520工况斗拱组各部分变形比例Table 8 Deformation scale for Dougong each part in condition P1520

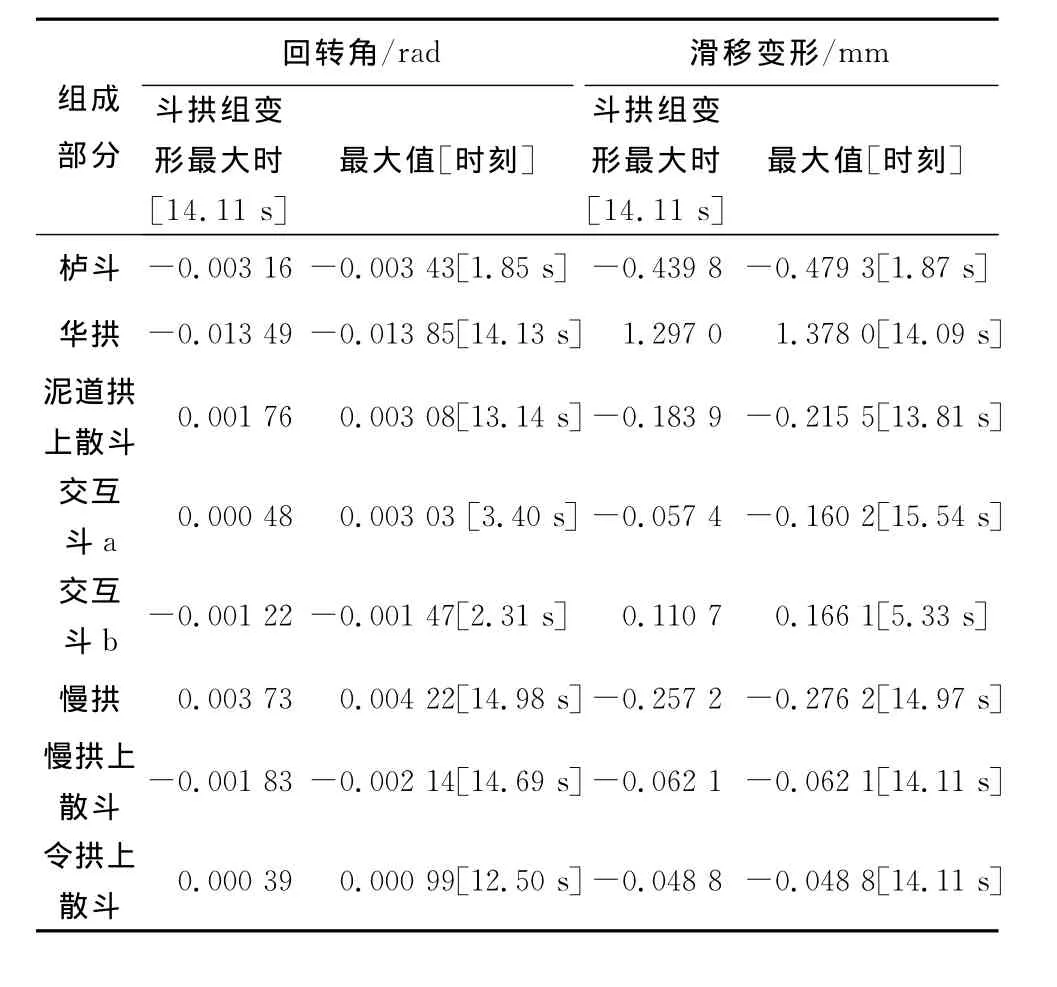
表9 P1530工况斗拱组各部分回转角和滑移值Table 9 Rotary and sliding displacement for Dougong each part in condition P1530

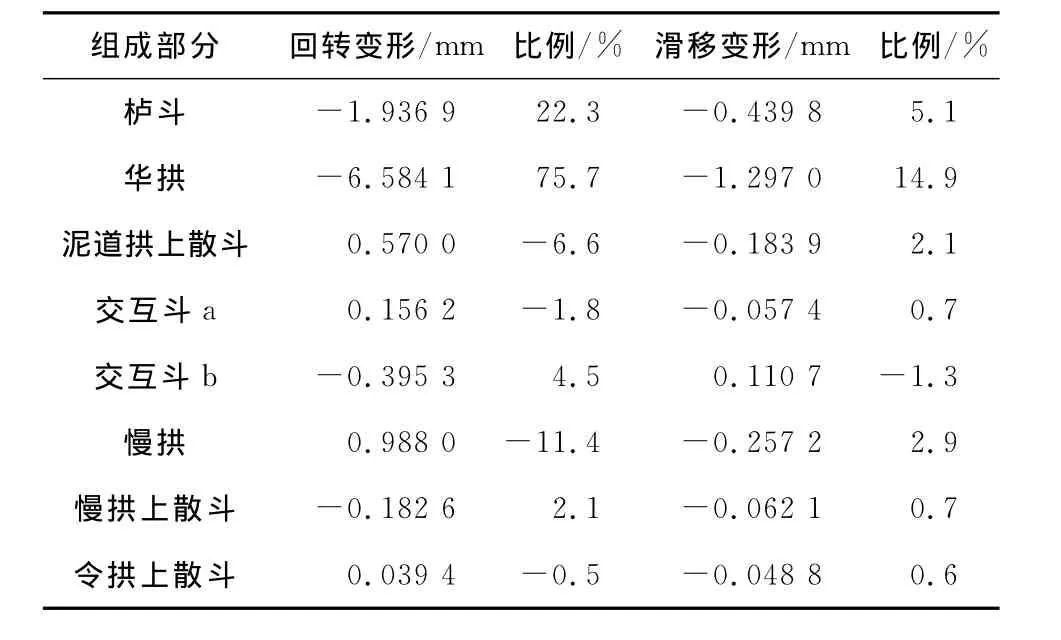
表10 P1530工况斗拱组各部分变形比例Table 10 Deformation scale for Dougong each part in condition P1520

从上表可以看出：1）斗拱模型整体回转角和滑移变形最大值出现时刻与各构件变形回转角和滑移变形最大值出现时刻非常相近，说明各构件变形最大值与斗拱整体变形最大值具有很强相关性。这种相关性在斗拱各层自下而上成递减趋势。2）由斗拱各部分变形比例计算数据结果显示，在输入振幅10 mm条件下，模型整体变形最大时，栌斗回转变形和滑移变形所占斗拱整体变形比例始终较大；当振幅增至20和30 mm时，随台面输入频率的增加，栌斗的回转变形占斗拱整体变形比例有所降低，而华拱回转变形所占比例有显著上升；栌斗和华拱的回转变形对斗拱的整体变形而言，处于支配地位。

进一步讨论栌斗和华拱在振动试验过程中的变化特征和抗震机理，分别绘制斗拱变形最大时刻栌斗和华拱在相同振幅不同频率下的回转位移及滑移位移曲线，如图8所示。

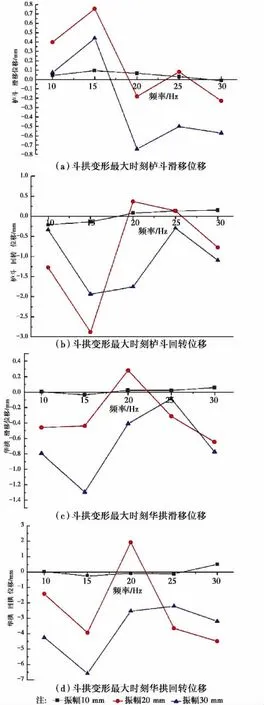
图8 斗拱变形最大时刻栌斗及华拱位移值Fig.8 Ludou and Huagong’s rotary and slipping deformation under maximal displacement

由图8可知：1）低频状态（1.05～1.59 Hz）下振幅对栌斗和华拱的回转位移及滑移位移影响较大，在频率1.59 Hz状态下影响最为显著；而随着台面输入振动频率的增加，振幅的影响逐渐降低，频率成为决定栌斗和华拱回转位移和滑移位移的主要因素。2）在低振幅状态（10 mm）下，频率对栌斗和华拱的回转位移及滑移位移影响并不明显，而当振幅增至20和30 mm时，栌斗和华拱的回转位移及滑移位移均有明显波动；在频率1.05～1.59 Hz时呈上升趋势，在1.59 Hz时达到最大，随后显著降低并在2.65 Hz时降至最低值，在频率继续增至3.12 Hz时又有所回升；频率1.59和2.65 Hz条件是栌斗和华拱回转位移和滑移位移变化的两个关键节点。结合前文，在频率1.59 Hz时，斗拱结构整体动力系数明显降低，而在2.65 Hz时斗拱动力系数基本保持稳定，说明频率1.59和2.65 Hz条件可能也是斗拱整体在地震作用下的变形特征和抗震机理变化的关键节点，在后续试验和研究中有待进一步验证。

3 结论

通过无缩尺甪直天王殿斗拱模型的振动台试验，探索松木斗拱的抗震机理，分析斗拱结构变形关键部位与薄弱环节，得出以下结论。

1）在振动过程中，斗拱通过构件之间榫卯连接处、斗与拱咬合处的摩擦及挤压耗能等达到减震作用；地震冲击越强，斗拱表现出的减震作用越明显。

2）模型各构件变形最大值斗拱整体变形最大值具有很强相关性，其中栌斗和华拱的回转变形对斗拱的整体变形而言，处于支配地位。

3）振幅是决定斗拱各构件水平向滑移峰值的主要因素；在振动过程中频率的变化对回转变形的变化程度起到重要作用，而对滑移位移的影响相对较小。

4）甪直天王殿柱头科斗拱的华拱连下昂部分主要起装饰作用，其前后两榫卯连接节点位置在振动过程中较为薄弱，在对实际文物维护修缮过程中应引起重视并采取相关加固措施。

5）试验中振动频率1.59和2.65 Hz条件是栌斗和华拱回转位移和滑移位移变化的两个关键节点，也是斗拱整体在地震作用下的变形特征变化的关键节点，在后续研究中有待进一步验证。

试验中存在一定不足，如选取单组斗拱作为试验体，在试验过程中易引起结构的失衡。此外，由于试验在空载状态下进行，对斗拱的转动约束较小，使其抗震耗能的作用未能充分发挥。故试验结果与实际有一定的误差，在后续试验中应进一步模拟实际荷载与叠加正弦振动，适当约束斗拱的转动；测定斗拱试件的自振频率，分析共振响应可能对试验结果带来的影响。

［1］盘锦章.中国木结构古建筑抗震机理分析［D］.上海：同济大学，2008.

［2］高大峰，赵鸿铁，薛建阳，等.中国古代木结构斗拱竖向承载力的试验研究［J］.世界地震工程，2003，19（3）：56-61.

Gao D F，Zhao H T，Xue J Y，et al.Experimental study on structural behavior of Dougong under the vertical action in Chinese ancient timber structure［J］.World Earthquake Engineering，2003，19（3）：56-61.（in Chinese）

［3］孙晓洁.殿堂型木构古建筑抗震机理分析——斗拱演化隔震的有限元动力分析［D］.成都：西南交通大学，2009.

［4］袁建力，陈韦，王珏，等.应县木塔斗栱模型试验研究［J］.建筑结构学报，2011，23（7）：66-72.

Yuan J L，Chen W，Wang J，et al.Experimental research on bracket set models of Yingxian Timber Pagoda［J］.Journal of Building Structures，2011，23（7）：66-72.（in Chinese）

Sui Y，Zhao H T，Xue J Y，et al.Experimental study on lateral stiffness of Dougong layer in Chinese historic buildings［J］.Engineering Mechanics，2010，27（3）：74-78.（in Chinese）

［6］邵云，邱洪兴，乐志，等.宋、清式斗拱低周反复荷载试验研究［J］.建筑结构，2014，44（9）：79-82.

Shao Y，Qiu H X，Yue Z，et al.Experimental study of low-cycle loading test on Song-style and Qing-style dougong［J］.Building Structure，2014，44（9）：79-82.（in Chinese）

［7］赵均海，俞茂鋐，杨松岩，等.中国古建筑木结构斗拱的动力实验研究 ［J］.试验力学，1999，14（1）：106-112.

Zhao J H，Yu M H，Yang S Y，et al.Dynamic experimental study on Dougong of ancient timber structures［J］.Journal of Experimental Mechanics，1999，14（1）：106-112.（in Chinese）

［8］方东平，俞茂鋐，宫本裕，等.木结构古建筑结构特性的计算研究［J］.工程力学，2001，18（1）：137-144.

Fang D P，Yu M H，Miyamoto Y，et al.Experimental studies on structural characteristics of ancient timber architectures［J］.Engineering Mechanics，2001，18（1）：137-144.（in Chinese）

［9］冯建霖，张海彦，王欢，等.古建筑大木作铺作层的振动分析［J］.四川建筑，2009，29（4）：132-133.

Feng J L，Zhang H Y，Wang H，et al.Vibration analysis of Dougong layer in ancient timber architectures［J］.Sichuan Architecture，2009，29（4）：132-133.（in Chinese）

［10］陈志勇，祝恩淳，潘景龙.中国古建筑木结构力学研究进展［J］.力学进展，2012，42（5）：645-653.

Chen Z Y，Zhu E C，Pan J L.Mechanics researching advance of Chinese ancient timber structure buildings［J］.Advance in Mechanics，2012，42（5）：645-653.（in Chinese）

［11］Kyuke H，Kusunoki T，Yamaoto M，et al.Shaking table tests of ‘MASUGUMI’used in traditional wooden architectures［C］∥In：10th World Conference on Timber Engineering，Miyazaki，2008.（in Japanese）

［12］陈从周.甪直保圣寺天王殿［J］.文物参考资料，1955，8：103-110.

Chen C Z.The Tianwang palace of Baosheng Temple in Luzhi［J］.Cultural Relics，1955，8：103-110.（in Chinese）

［13］樊剑，吕超，张辉.地震波的时频特征及其对结构地震反应的影响［C］∥第17届全国结构工程学术会议文集（Ⅲ），2008：014-018.

Fan J，Lv C，Zhang H.Study on the time—frequency characteristic of ground motions and its effect on structural earthquake response［C］∥In：Proceedings of the 17th National Conference on Structural Engineering（Ⅲ），2008：14-18.（in Chinese）

（编辑 吕建斌）

2014-12-26

Projects in the National Science ＆ Technology Pillar Program during the Twelfth Five-year Plan Period（No.2012BAD24B010204）；A Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions（No.PAPD201104）；National Undergraduate Training Programs for Innovation and Entrepreneurship（No.201410298016Z）

Author brief：Que Zeli（1973-），PhD，associate professor，main research interest：timber architecture design，building aseismatic capability，and new wood-based engineering composite materials，（E-mail）zelique.nfu＠gmail.com.

Experimental analysis on shaking table tests of Dougong in Tianwang Hall，Luzhi，Ming dynasty

Que Zeli，Li Zherui，Zhang Beibei，Hou Tongyu，Pan Biao

（Department of Wooden Architecture，Nanjing Forestry University，Nanjing 210037，P.R.China）

Taking the Dougong of Tianwang palace in Baosheng Temple，Luzhi as a case，experimental study was carried out on shaking table tests of the full-scale pine Dougong model.Analysing the acceleration and dynamic magnification coefficient trends，the process of displacement characteristics of Dougong in response to changes of vibration，and the rotary and sliding displacement values of Dougong and each component at the biggest deformation moments.Major conclusions are as follows，Seismic acceleration indicates the response of seismic intensity，instead of the maximum deformation of the Dougong specimens.Vibration frequency has important influence on the degree of rotation deformation，while amplitude has decisive effect on the sliding displacement of each component.The maximum deformation of Dougong and each component all have a strong correlation，among which the rotary displacement of Ludou and Huagong occupies a dominant position.Huagong with xia-ang，which is a special part of Dougong，is mainly for decoration and it＇s weak on connection node position during the shaking table tests.So more attention and relevant reinforcement measures should be taken on this part in the maintenance and conservation of cultural relics.

timber structure；Dougong；pine；shaking table test；anti-seismic mechanism

TU366.2

A

1674-4764（2015）03-0026-09

10.11835／j.issn.1674-4764.2015.03.004

2014-12-26

“十二五”国家科技项目（2012BAD24B010204）；江苏高校优势学科建设工程项目（PAPD201104）；国家级大学生创新创业训练计划（201410298016Z）

阙泽利（1973-），男，副教授，博士，主要从事木结构建筑设计、抗震性能及新型木质工程复合材料研究，（E-mail）zelique.nfu＠gmail.com。