基于仿射奇异线性空间构造压缩感知矩阵
2015-03-06高有,王刚
高 有,王 刚
(中国民航大学理学院,天津 300300)
基于仿射奇异线性空间构造压缩感知矩阵
高 有,王 刚
(中国民航大学理学院,天津 300300)
基于仿射奇异线性空间的子空间面之间的关联关系,构造了一个新的压缩感知矩阵,计算了所构造的压缩感知矩阵的相关性,并得到处理信号可以恢复的最大稀疏度,同时,与Ronald A DeVore利用有限域上的多项式构造的压缩感知矩阵进行比较,当两个压缩感知矩阵处理信号的有效率相同时,基于仿射奇异线性空间构造的压缩感知矩阵处理信号的最大稀疏度优于Ronald A.DeVore构造的压缩感知矩阵处理信号的最大稀疏度。
压缩感知矩阵;仿射奇异线性空间;相关性;稀疏度
压缩感知理论在信号处理过程中扮演着重要的角色,其主要目的是通过较少的测量次数对信号进行观测来获取信号的主要信息,进而能准确或高概率恢复信号。给定一个离散信号x∈Rn(实数域R上的n维列向量),利用m个线性投影来测量信号x,并把这m个线性投影组成的m×n阶矩阵φ叫做压缩感知矩阵,并把y=φx称为测量向量。
如果一个信号x∈Rn中至多有k个非0分量,则称x是k-稀疏信号。对于一个给定的测量向量y,如何将原始信号x从y=φx中恢复出来,Donodo和Candes等[1-2]充分利用信号的稀疏性质,通过寻找线性方程y=φx的稀疏解问题

即可得到原始稀疏信号x的信息。而给定一个矩阵,如何判断其是否适合作为压缩感知矩阵,Candes等[2]给出被广泛接受的判断标准——受限等距性。设φ是一个m×n阶矩阵,如果存在一个常数0≤δk<1,使得对于任意k-稀疏的信号x∈Rn,均有如下不等式成立
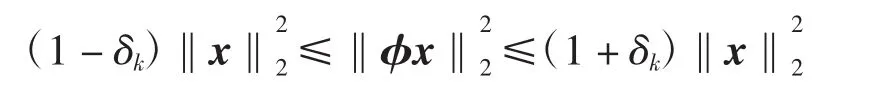
则称矩阵φ满足k阶受限等距性,满足上式的最小非负实数δk称为k阶受限等距常数。设矩阵φ的列向量为(a1,a2,…,an),则矩阵φ的相关性为

由于低相关性可以导出受限等距性[3],因此只要一个矩阵的相关性足够低即可用来测量信号。
引理1[4]设矩阵φ的相关性为μ,则对于所有矩阵φ都满足k阶受限等距性,受限等距常数δk≤μ(k-1)。
DeVore[5]利用有限域上次数不大于r的多项式构造相关性是的感知矩阵;Li Shuxing等[6-7]利用代数曲线和有限几何构造了感知矩阵;Bourgain等[3]利用加法组合学构造了m×n的感知矩阵,其中受限等距性的阶为是任意选定的实数;Zhao Xianghui等[8]利用伪辛空间中子空间的关联关系构造了新的池设计。
本文基于仿射奇异线性空间构造了压缩感知矩阵,计算了其相关性,并得到了构造的压缩感知矩阵可恢复的信号最大稀疏度,并与DeVore利用有限域上多项式构造的压缩感知矩阵进行比较,当两个压缩感知矩阵处理信号的有效率相同时,基于仿射奇异线性空间构造的压缩感知矩阵处理信号的最大稀疏度优于Ronald A.DeVore构造的压缩感知矩阵处理信号的最大稀疏度。
1 预备知识
仿射奇异线性空间的概念[9-11]介绍如下。


2 压缩感知矩阵的构造
首先回顾DeVore[5]构造的大小为p2×pr的感知矩阵。设Fp是一个有限域,其中p是一个素数,Pr表示有限域Fp上所有次数不超过r-1的多项式组成的集合,所以任意一个多项式f∈Pr,可将f看成是从Fp到Fp得映射,对于取定的一个多项式f,记二元列向量vf为


设GA(n+l,n;Fq)是Fq上的(n+l)-维仿射奇异线性空间,集合G表示(n+l)-维仿射奇异线性空间GA(n+l,n;Fq)中所有(m1,s1)-面的集合,其中0≤s1≤ l,0≤m1-s1≤n,即M)是GA(n+l,n;Fq)中不同的(m1,s1)-面,M=O(m1,s1;n+l,n)。集合H表示(n+l)-维仿射奇异线性空间GA(n+l,n;Fq)中所有(m,s)-面的集合,其中0≤s≤l, 0≤m-s≤n,即N)是GA(n+l,n;Fq)中不同的(m,s)-面,N=O(m,s;n+ l,n)。
设φ0=(aij)M×N是一个{0,1}-矩阵,其中
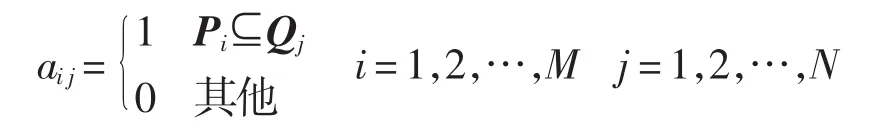
{0,1}-矩阵φ0的每一列中1的个数L等于GA(n+l,n;Fq)中包含在给定的(m,s)-面的(m1,s1)-面的个数。由引理3,知


由引理1可知,对于所有的k<q(m1+1)+1,矩阵φ0都满足k阶受限等距性,所以信号可以恢复的最大稀疏度为

令k1=0,有m1≤m-s≤n,则kmax=q(n+1),而此时所构造矩阵的行数与列数之比为
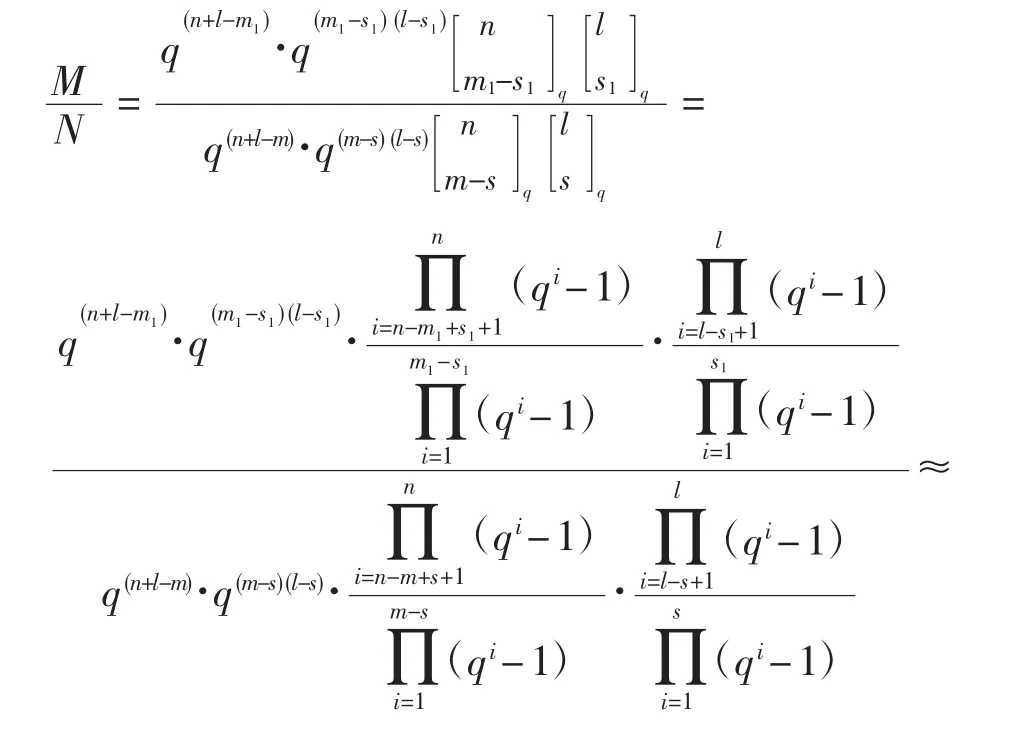

已知DeVore利用有限域上多项式构造的压缩感知矩阵的行数与列数之比为

且最大稀疏度为

这样得到最大稀疏度kmax>k′max。
[1]DONOHO D.Compressed sensing[J].IEEE Trans Inform Theory,2006,52:1289-1306.
[2]CANDES E,ROMBERG J,TAO T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J]. IEEE Trans Inform Theory,2006,52:489-509.
[3]BOURGAIN J,DILWORTH S,FORD K,et al.Explicit constructions of RIP matrices and related problems[J].Duke Math J,2011,159:145-185.
[4]CANDES E.The restricted isometry property and its implications for compressed sensing[J].CR Math Acad Sci Paris,2008,346:589-592.
[5]DEVORE R.Deterministic constructions of compressed sensing matrices[J].J Complexity,2007,23:918-925.
[6]LI SHUXING,GAO FEI,GE GENNIAN,et al.Deterministic construction of compressed sensing matrices via algebraic curves[J].IEEE Trans.Inform Theory,2012,58:5035-5041.
[7]LI SHUXING,GE GENNIAN.Deterministic construction of sparse sensingmatricesviafinitegeometry[J].IEEETrans on Signal Processing,2014,62:2850-2859.
[8]ZHAO XIANGHUI,XU NING,ZHANG GENGSHENG.New pooling design constructed with pseudo-symplectic[J].Chin Quart J of Math,2012,27:526-534.
[9]ZHANG MANLI,JIE CUNLAI.Anzahl theorems of flats in affine singular linear spaces and their applications[J].Journal of Hebei Normal University(Natural Science Edition),2012,36:560-563.
[10]WAN ZHEXIAN.Geometry of Classical Groups Over Finite Fields[M]. 2nd ed.Beijing:Science Press,2002.
[11]WANG KAISHUN,GUO JUN,LI FENGGAO.Singular linaer space and its application[J].Finite Fields App,2011,17:395-406.
(责任编辑:杨媛媛)
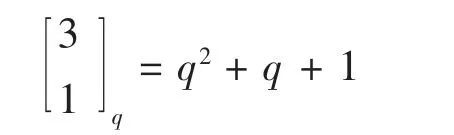
从而

2)设m、m′是两个同时对编码规则e有效的不同报文,且m∩L≠m′∩L。若m与m′不相交,则不存在这样的编码规则。若m与m′相交,则由维数公式可知,m∩m′是一个平面,且与L不相交。该平面上任意一条直线均是对m、m′同时有效的编码规则。从而
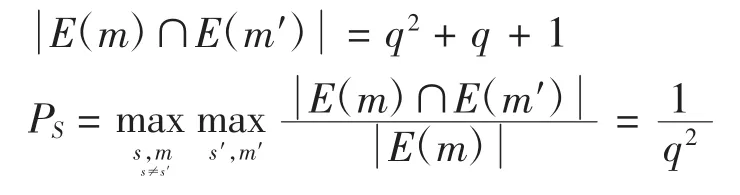
参考文献:
[1]SIMMONS G J.Authentication theory/decoding theory[J].Lecture Notes in Computer Science,1985,96:411-431.
[2]LIANG M,DU B L.A new class of 3-fold perfect splitting authenticationcodes[J].DesignCodesCryptography,2012,62:109-119.
[3]CHEN S D,ZHAO D W.Construction of multi-receiver multi-fold authentication codes from singular sympletic geometry over finite fields[J]. Algebra Colloquium,2013,20(4):701-710.
[4]CHEN S D,ZHAO D W.New construction of authentication codes with arbitration from pseudo-sympletic geometry over finite fields[J].Ars Combinatoria,2010,97(A):453-465.
[5]GAO Y,LIU Y Q.The construction of A3-code from projective spaces over finite fields[J].WSEAS Transactions on Mathematics,2013,12(10):1024-1033.
[6]SIMMONS G J.A game theory model of digital message authentication [J].Congr Numer,1982,34:413-424.
[7]KUROSAWA K,OBANA S.Combinatorial bounds on authentication codes with arbitration[J].Designs Codes Cryptography,2001,22:265-281.
[8]王永传,杨义先.分裂认证码与纠错码[J].通信保密,1999,77(1):64-66.
[9]HUBER M.Combinatorial bounds and characterizations of splitting authentication codes[J].Cryptography and Communications,2010,2:173-185.
[10]WAN Z X.Geometry of Classical Groups over Finite Fields[M].2nd ed. Beijing:Science Press,2002.
(责任编辑:杨媛媛)
Construction of compressed sensing matrix based on affine singular linear spaces
GAO You,WANG Gang
(College of Science,CAUC,Tianjin 300300,China)
A compressed sensing matrix based on correlations of subspace flats in the affine singular linear spaces is constructed and the coherence of the matrix is computed.Meanwhile,the maximum sparsity of the matrix is obtained.Finally,a comparision is made with the matrix constructed by Ronald A DeVore based on polynomials over finite fields and the maximum sparsity of the current matrix is better than that of the matrix constructed by Ronald A DeVore when the efficiencies of the two matrices are equal.
compressed sensing matrix;affine singular linear space;coherence;sparsity
O157.2
:A
:1674-5590(2015)06-0061-04
2014-08-05;
:2014-10-10
中央高校基本科研业务费专项(SY-1416);中国民航大学学生(波音)技术挑战资助基金项目(20140159201)
高有(1966—),男,内蒙古化德人,教授,博士,研究方向为代数、密码与编码.
