基于最优REQUEST/CKF组合的航天器姿态确定

肖支才,李海君,王 朕

(海军航空工程学院,山东烟台 264001)



基于最优REQUEST/CKF组合的航天器姿态确定

肖支才,李海君,王 朕

(海军航空工程学院,山东烟台 264001)

针对航天器姿态确定的高精度要求,提出一种基于最优递推四元数估计/容积卡尔曼滤波(REQUEST/CKF)的姿态估计器。该方法将最优递归四元数估计(REQUEST)方法和容积卡尔曼滤波(CKF)结合起来,用最优REQUEST方法确定的姿态四元数直接作为CKF滤波器的观测量,由CKF滤波估计陀螺漂移来补偿系统模型误差,从而提高了姿态确定的精度和收敛速度。仿真结果说明了方法的有效性。

航天器姿态确定;惯性/天文组合;最优递归四元数估计;容积卡尔曼滤波

0 引言

基于星敏感器和陀螺仪组合的航天器定姿方法是较为有效的定姿方案之一[1]。此定姿方案常用的滤波算法是EKF[2]，但该算法对于较强的非线性系统时，常存在精度低的问题。在航天器姿态确定的各种算法中UKF[3]得到广泛的使用，但UKF计算量较大，并且算法使用中参数的选择难度较大。随着非线性滤波方法的发展，航天器姿态确定领域也出现了一些新的算法，如粒子滤波算法[4]、高斯滤波算法[5]、多模自适应估计算法[6]等。文献[7]将基于矢量观测的姿态确定算法与EKF方法相结合提出了一种分段信息融合的姿态估计器来实现高精度定姿,取得了较好的滤波效果,但EKF固有的缺点使得滤波精度受到很大限制。

以四元数为姿态参数确定航天器姿态的递推四元数估计(REQUEST)[8],不仅可以顺序处理观测的星光矢量,且只有单星的情况下也能进行姿态确定。

近年来,文献[9-10]提出了容积卡尔曼滤波(cubature kalman filter,CKF),为非线性估计问题提供了一种新的实现方式。与其他的非线性方法相比,CKF算法具备更优的非线性逼近性能、数值精度以及滤波稳定性,且CKF实现简单和滤波精度较高。文献[11]将CKF用于卫星的姿态估计,给出了容积四元数估计器,并与信息滤波结合提出容积信息四元数估计器,用以解决初始估计误差大的姿态估计问题。但该方法没有考虑矢量测量四元数的精度问题,使得矢量测量四元数的误差影响了整个滤波的精度。

文中结合REQUEST和CKF各自的优点提出一种惯性/天文组合的定姿方法,以满足航天器高精度的定姿要求。该方法将最优REQUEST方法嵌入到CKF滤波器中,将最优REQUEST方法确定的四元数直接作为CKF滤波器的观测量,由CKF滤波器估计陀螺漂移来补偿最优REQUEST的系统模型误差。仿真结果表明这种方法可达到较高的滤波精度。

1 问题的描述和分析

1.1 航天器姿态确定的四元数描述

由姿态四元数描述的航天器姿态,其运动学方程的线性形式能够得到解析解。文中采用四元数进行姿态描述,建立的状态方程和量测方程如下:

1)状态方程

姿态四元数满足正交约束条件,如果选择其4个分量作为状态变量,则所构成方差阵必是奇异的;随着方差的递推,这种奇异性很难得到保证。因此,在基于CKF滤波的航天器姿态确定中,直接取四元数的矢量部分e和陀螺漂移估计误差b、gsf、gma为状态变量:X=[ebgsfgma]T。

由四元数运动学方程有:

(1)

则可得系统状态方程为:

(2)

2)量测方程

星敏感器是根据星光矢量信息确定航天器的体坐标系相对于惯性坐标系的姿态四元数qm;将qm作为CKF滤波器的观测量,其量测方程为:

qm=q⊗qv

(3)

式中:qv为星敏感器精度的误差四元数,一般可近似为qv=[vT,1]T;v是高斯白噪声向量。取qm的矢量部分e作为量测量,则可得量测方程为:

e=HX+v=[I3×303×12]X+v

(4)

1.2 滤波方法分析

1)CKF滤波

考虑如下加性噪声离散非线性动态系统:

xk=f(xk-1)+wk-1

zk=h(xk)+vk

(5)

式中:xk为系统状态向量;zk为量测值。假定过程噪声wk-1和量测噪声vk相互独立,且wk～(0,Qk-1),vk～(0,Rk)。

CKF方法首先计算加权函数为标准正态分布密度的积分的基本容积点和对应的权值:

(6)

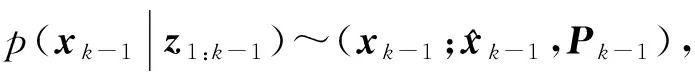
1)时间更新

①计算容积点

(7)

②计算通过非线性状态方程传播的容积点

(8)

③计算状态和方差预测

(9)

2)量测更新

①分解因式

(10)

②计算容积点

(11)

③计算通过非线性量测方程传播的容积点

Zj,k=h(Xj,k)

(12)

④计算量测预测、新息方差和协方差估计

(13)

⑤计算增益、状态和协方差估计

(14)

2 最优REQUEST与CKF的组合定姿

2.1 最优REQUEST算法

最优REQUEST算法以K矩阵为状态变量,只需要各个时刻的惯性角速度和星光矢量就能顺序地估计各个时刻的K矩阵。最优四元数是K矩阵的最大特征值的特征向量。K矩阵的动力学和测量模型的方程是:

(15)

(16)

其中,其中Φk是转动角速度矢量的正交矩阵函数;Wk和Vk+1分别为过程噪声矩阵和测量噪声矩阵。

时间更新和量测更新如下:

1)时间更新方程

(17)

(18)

2)量测更新方程

2.2 CKF+最优REQUEST双重滤波器设计

以CKF滤波器为外框架,将最优REQUEST滤波器嵌入到CKF滤波器中,具体流程如下:

1)确定CKF滤波器的状态初值:根据星光矢量观测,利用四元数估计(QUEST)确定K矩阵的初值;从K矩阵中分离出四元数,取矢量部分作为CKF滤波器e部分的初值,同时给定陀螺漂移初值b、gsf、gma。

2)在一步预测前,对陀螺漂移进行补偿,即从测量的角速度中减去陀螺漂移;然后计算容积点和相应的权值。

3)根据计算的容积点和相应的权值进行时间更新,求解状态和方差预测。

4)如果有星光矢量信息输入,则用最优REQUEST算法递推K矩阵;并从K矩阵中分离出四元数,取矢量部分作为CKF的观测量,进行CKF的量测更新,回到步骤2),继续下一个循环。

组合定姿工作原理如图1所示。

图1 组合定姿估计器工作原理

3 仿真分析

对上述方法进行计算仿真,航天器姿态确定使用恒星敏感器/陀螺的组合定姿方式,设定初始仿真条件:恒星敏感器测量精度为3.6″(1σ),更新频率为1 Hz,假设星敏感器可观测到3个星光矢量;陀螺采样频率为100 Hz,陀螺漂移为20°/h(1σ),陀螺随机噪声标准差为0.2°/h;假定星敏感器坐标系与航天器本体坐标系的Z轴反方向一致,航天器体坐标系X轴与星敏感器坐标系X轴重合,导航坐标系为J2000坐标系,仿真时间为500 s。滤波方法分别选择单独运用CKF方法和REQUEST/CKF组合滤波方法进行仿真,仿真结果见图2～图4。

图2和图3分别展示了基于CKF的姿态角估计误差和陀螺漂移误差曲线及基于REQUEST/CKF组合的姿态角估计误差和陀螺漂移误差曲线,由仿真结果可以看出,单纯基于CKF滤波定姿的估计误差大约在200 s收敛,而基于REQUEST/CKF组合定姿估计误差在150 s就收敛到一定的误差水平。图4以滚动角估计误差和X轴陀螺漂移估计误差为例说明了收敛后的估计误差精度,由图可看出,基于CKF定姿的姿态角估计误差最终精度大约为0.3″,陀螺漂移估计误差为0.26°/h,而基于REQUEST/CKF组合定姿的姿态角估计误差大约为0.2″,陀螺漂移估计误差为0.2°/h,其精度有所提高。这是因为将REQUEST嵌入到CKF后,使得CKF所用的量测量的精度提高,从而使滤波收敛速度加快,滤波精度提高。

图3 基于REQUEST/CKF的姿态角估计误差和陀螺漂移估计误差

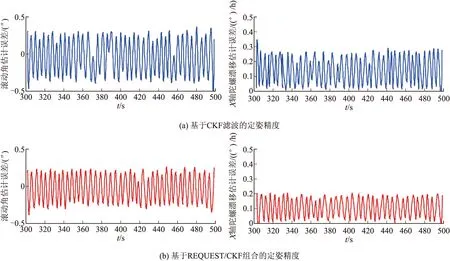
图4 两种方法的估计精度

4 结论

针对航天器姿态确定的高精度要求,提出了一种基于星敏感器/陀螺组合的定姿方法,结合矢量测量的最优REQUEST和CKF各自的特点设计双重滤波器。最优REQUEST引入了卡尔曼滤波结构,有效估计最优渐消因子和简化滤波的设计过程,由CKF估计陀螺漂移误差来补偿最优REQUEST的系统模型误差,从而实现高精度定姿。仿真结果表明了方法的有效性。

[1] LIN Yurong, DENG Zhenglong. Mode-error-based predictive filter for satellite attitude determination [J]. Journal of Astronautics, 2001, 22(1): 79-88.

[2] LEFFERTS E J, MARKLEY F L, SHUSTER M D. Kalman filtering for spacecraft attitude estimation [J]. Journal of Guidance, Control, and Dynamics, 1982, 5(5): 417-429.

[3] CRASSIDIS J L, MARKLEY F L. Unscented filtering for spacecraft attitude estimation [J]. Journal of Guidance, Control, and Dynamics, 2003, 26(4): 536-542.

[4] OSHMAN Y, CARMI A. Attitude estimation from vector observations usin g genetic-algorithm-embedded quaternion particle filter [J]. Journal of Guidance, Control, and Dynamics, 2006, 29(4): 879-891.

[5] LINARES R, KUMAR V, SINGLA P. Information theoretic space object data association methods usin g an adaptive Gaussian sum filter [J]. Advances in the Astronautical Sciences, 2011, 140: 665-680.

[6] LAM Q M, CRASSIDIS J L. Evaluation of a multiple model adaptive estimation scheme for space vehicle’s enhanced navigation solution [C]∥ Collection of Technical Papers-AIAA Guidance, Navigation, and Control, 2007: 4690-4710.

[7] 于延波, 房建成. 基于矢量观测的航天器分段信息融合定姿方法 [J]. 北京航空航天大学学报, 2005, 31(11): 1254-1258.

[8] CHOUKROUN D, OSHMAN Y. Optimal request algorithm for attitude determination [C]∥AIAA Guidance, Navigation, and Control Con fence and Exhibit, 2001: 1-9.

[9] ARASARATNAM I, HAYKIN S. Cubature Kalman filters [J]. IEEE Trans. On Automatic Control, 2009, 54(6): 1254-1269.

[10] ARASARATNAM I, HAYKIN S. Cubature Kalman filtering for continuous-discrete systems: Theory and simulations [J]. IEEE Trans. On Signal Processin g, 2010, 58(10): 4977-4993.

[11] 魏喜庆, 宋申民. 基于容积卡尔曼滤波的卫星姿态估计 [J]. 宇航学报, 2013, 34(2): 193-200.

Spacecraft Attitude Determination of REQUEST/CKF Integration

XIAO Zhicai,LI Haijun,WANG Zhen

(Naval Aeronautical and Astronautical University Shandong Yantai 264001, China)

According to high-precision requirement for spacecraft attitude determination, an integrated REQUEST/CKF attitude determination method was proposed. This method combines different characteristics of vector observation attitude determination algorithm and CKF algorithm to achieve high-precision attitude determination. The algorithm combines REQUEST and CKF. The quaternion determined by REQUEST is directly used as CKF filter observations, and CKF filter estimates gyro drift so that it can compensate for model error. Simulation results show effectiveness of the method.

spacecraft attitude determination; INS/CNS integration; optimal-REQUEST; cubature Kalman filter

2014-11-05

航空科学基金资助

肖支才(1977-),男,湖北武汉人,副教授,博士,研究方向:导航与制导。

V249.3

A